Group Multiple Criteria Decision Making: Multiset Approach

Abstract

The chapter describes a new approach to solve problems of group multiple criteria decision making. New methods for group sorting and ordering objects, presented with many quantitative and qualitative attributes, are based on the theory of multiset metric spaces. The suggested techniques were applied to the expertise of R&D projects in the Russian Foundation for Basic Research. For selection of competitive applications and multiple criteria evaluation of project efficiency, several experts evaluated projects upon many verbal criteria.

This work is partially supported by the Russian Academy of Sciences, Research Programs “Information, Control and Intelligent Technologies and Systems”, “Intelligent Information Technologies, Systems Analysis and Automation”; the Russian Foundation for Basic Research, Projects No 11-07-00398, 14-07-00916; the Russian Foundation for Humanities, Projects No 12-02-00525, 12-33-10608, 14-32-13004.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Sorting objects into several classes and ordering objects by their properties are the typical problems of multiple criteria decision making (MCDM), pattern recognition, data mining, and other areas. These problems are formulated as follows. Let A ₁, …, A _n be a collection of objects, which are described by m attributes Q ₁, …, Q _m . Every attribute has its own scale $X_{s} = \{ x_{s}^{1}, \ldots ,x_{s}^{{h_{s} }} \} ,$ s = 1, …, m, grades of which may be numerical, symbolic or verbal, discreet or continuos, nominal or ordinal. Ordinal grades are supposed to be ordered from the best to the worst. Attributes may have different relative importance (weights). The attribute list depends on the aim of decision analysis. It is required to range all multi-attribute objects or assign every object to one of the given classes (categories) C ₁, …, C _g , describe and interpret the properties of these classes of objects. The number g of object classes can be arbitrary or predefined, and the classes can be ordered or unordered.

In the case of group decision making, one and the same multi-attribute object is represented in k versions or copies, which are usually distinguished by attribute values. For example, object characteristics have been measured in different conditions or in different ways, either several experts independently evaluated objects upon many criteria.

One of basis points in MCDM area [4–6, 8–11, 14–21] is preferences of decision maker (DM) and/or expert. The person expresses his/her preferences when he/she describes properties and characteristics of the analyzed problem, compares decision alternatives, estimates the choice quality. Preferences may be represented as decision rules of mathematical, logical and/or verbal nature and explained with any language. While solving the problem, a person may behave inconsistently, make errors and contradictions. In the case of individual choice, the consistency of subjective preferences is postulated. In order to discover and correct possible inconsistent and contradictory judgments of a single DM, special procedures have to be included in MCDM methods [10].

A collective choice of several independent actors is more complicate and principally different due to a variety and inconsistency of many subjective preferences. Every DM may have his/her own personal goals, interests, valuations and information sources. As a result, individual subjective judgements of actors may be similar, concordant or discordant. Usually, in MCDM techniques, one tries to avoid possible inconsistencies and contradictions between judgements of several persons. Often many diverse points of view are replaced with a single common preference that is aggregated mostly all individual opinions. But individual preferences may be coordinated not always. Nevertheless, most of the decision methods do not pay a consideration to contradictions and inconsistencies in DMs’ preferences.

In this chapter, we consider methods for group ordering and classifying objects, which are presented with many numerical and/or verbal attributes and may exist in several copies. These methods are based on the methodology of group verbal decision analysis and the theory of multiset metric spaces [9, 10, 13–18]. The suggested techniques were applied to real-life case studies in various practical areas, where several experts estimated objects upon many qualitative criteria.

2 Representation of Multi-Attribute Objects

In MCDM problems, a multi-attribute object A _i is represented as a vector or tuple (cortege) ${\varvec{x}}_{i} = (x_{i1}^{{e_{1} }} , \ldots ,x_{im}^{{e_{m} }} )$ in the Cartesian m-space X ₁ × ··· × X _m of attributes scales. Often qualitative variables are transformed in the numerical ones by one or another way, for example, using the lexicographic scale or fuzzy membership functions [6, 20, 21]. Unfortunately, the admissibility and validity of similar transformations of qualitative data into quantitative ones are not always justified. In methods of verbal decision analysis [9, 10], objects are described by qualitative variables without a transformation into numerical attributes.

The situation becomes more complicated when one and the same object exist in multiple versions or copies. Then, not one vector/cortege but a group of vectors/corteges corresponds to each object. So, an object A _i is represented now as a collection of k vectors/corteges $\left\{ {{\varvec{x}}_{i}^{( 1)} , \ldots ,{\varvec{x}}_{i}^{(k)} } \right\}$ where ${\varvec{x}}_{i}^{\left( j \right)} = (x_{i 1}^{{e_{ 1} \left( j \right)}} ,\ldots,x_{im}^{{e_{m} \left( j \right)}} ),$ $j = 1, \ldots ,k.$ And this group should be considered and treated as a whole in spite of a possible incomparability of separate vectors/corteges x ^(j) _i . A collection of multi-attribute objects can have an overcomplicated structure that is very difficult for analysis.

In many group decision methods, a collection of k vectors $\left\{ {{\varvec{x}}_{i}^{( 1)} , \ldots ,{\varvec{x}}_{i}^{(k)} } \right\}$ is replaced usually by a single vector y _i . Typically, this vector y _i has the components derived by averaging or weighting the values of attributes of all members of the group, or this vector is to be the mostly closed to all vectors within a group or to be the center of group. Note, however, that features of all initial vectors ${\varvec{x}}_{i}^{\left( 1\right)} , \ldots ,{\varvec{x}}_{i}^{(k)}$ could be lost after such replacement. The operations of averaging, weighing, mixing and similar data transformations are mathematically incorrect and unacceptable for qualitative variables. Thus, a group of objects, represented by several tuples, can not be replaced by a single tuple. So, we need new tools of aggregation and work with such objects.

Let us consider another way for representing multi-attribute objects. Define the combined attribute scale or the hyperscale X = X ₁ ∪ ··· ∪ X _m that is a set consisted of m attribute (criteria) scales $X_{s} = \{ x_{s}^{{e_{s} }} \}$. Now represent an object A _i as the following set of repeating attributes

$$ \begin{aligned} {\varvec{A}}_{i} &= \{ k_{{\varvec{A}}i} \left( {x_{1}^{1} } \right)\circ x_{1}^{1} , \ldots ,k_{{\varvec{A}}i} \left( {x_{1}^{{h_{1} }} } \right)\circ x_{1}^{{h_{1} }} , \ldots , \\ & \quad k_{{\varvec{A}}i} \left( {x_{m}^{1} } \right)\circ x_{m}^{1} , \ldots ,k_{{\varvec{A}}i} \left( {x_{m}^{{h_{m} }} } \right)\circ x_{m}^{{h_{m} }} \} . \\ \end{aligned} $$

(1)

Here $k_{{\varvec{A}}i} (x_{s}^{{e_{s} }} )$ is a number of attribute $x_{s}^{{e_{s} }}$, which is equal to a number of experts evaluated the object A _i with the criterion estimate $x_{s}^{{e_{s} }}$, or a number of different conditions or instruments used to measure an attribute value $x_{s}^{{e_{s} }}$; the sign ∘ denotes that there are $k_{{\varvec{A}}i} (x_{s}^{{e_{s} }} )$ copies of attribute $x_{s}^{{e_{s} }} \in X_{s}$ within the description of object A _i .

Thus, the object A _i is represented now as a set of many repeating elements x (for instance, attribute values $x_{s}^{{e_{s} }}$) or as a multiset ${\varvec{A}}_{i} = \{ k_{{\varvec{A}}i} \left( {x_{ 1} } \right)\circ x_{ 1}$, $k_{{\varvec{A}}i} \left( {x_{ 2} } \right)\circ x_{ 2} , \ldots \}$ over the ordinal (crisp) set X = {x ₁, x ₂, …} that is defined by a multiplicity function $k_{\varvec{A}} :X \to {\mathbf{Z}}_{ + } = \left\{ {0, 1, 2, 3, \ldots } \right\}$ [2, 7, 13]. A multiset A _i is said to be finite when all numbers k _{A i} (x) are finite. Multisets A and B are said to be equal (A = B), if k _A (x) = k _B (x). A multiset B is said to be included in a multiset A (B ⊆ A), if k _B (x) ≤ k _A (x), ∀x∈X.

There are defined the following operations with multisets:

• union A∪B, k _A∪B (x) = max[k _A (x), k _B (x)];

• intersection A∩B, k _A∩B (x) = min[k _A (x), k _B (x)];

• arithmetic addition A + B, k _A+B (x) = k _A (x) + k _B (x);

• arithmetic subtraction A− B, k _A−B (x) = k _A (x) − k _A∩B (x);

• symmetric difference A ∆ B, k _{A ∆ B} (x) = |k _A (x) − k _B (x)|;

• multiplication by a scalar b ·  A, k _b·A (x) = b · k _A (x), b > 0;

• arithmetic multiplication A · B, k _{A · B} (x) = k _A (x) · k _B (x);

• direct product A × B, k _A×B (x _i , x _j ) = k _A (x _i ) · k _B (x _j ), x _i ∈A, x _j ∈B.

A collection A ₁, …, A _n of multi-attribute objects may be considered as points in the multiset metric space (L(Z), d) with the following types of distances

$$ \begin{aligned} d_{1p} \left( {{\varvec{A}},{\varvec{B}}} \right) & = [m({\varvec{A}} \Delta {\varvec{B}})] {^{1/p} ;d_{2p} \left( {{\varvec{A}},{\varvec{B}}} \right) = } [m({\varvec{A}} \Delta {\varvec{B}})/m\left( {\varvec{Z}} \right)]^{1/p} ; \\ d_{3p} \left( {{\varvec{A}},{\varvec{B}}} \right) & = [m({\varvec{A}} \Delta {\varvec{B}})/m({\varvec{A}} \cup {\varvec{B}})]^{1/p} , \\ \end{aligned} $$

(2)

where p ≥ 0 is an integer, the multiset Z is the so-called maximal multiset with k _Z (x) = max _A k _A (x), and m(A) is a measure of multiset A.

Multiset measure m is a real-valued non-negative function defined on the algebra of multisets L(Z). The maximal multiset Z is the unit and the empty multiset ∅ is the zero of the algebra. A multiset measure m has the following properties: m(A) ≥ 0, m(∅) = 0; strong additivity m(∑ _i A _i ) = ∑ _i m(A _i ); weak additivity m(∪ _i A _i ) = ∑ _i m(A _i ) for A _i ∩A _j  = ∅; weak monotony m(A) ≤ m(B)⟺A ⊆ B; symmetry m(A) + m($\overline{\varvec{A}}$) = m(Z); continuity lim _i→∞ m(A _i ) = m(lim _i→∞ A _i ); elasticity m(b · A) = bm(A).

The distances d _2p (A, B) and d _3p (A, B) satisfy the normalization condition 0 ≤ d(A, B) ≤ 1. d _3p (∅, ∅) = 0 by the definition, while the distance d _3p (A, B) is undefined for A = B = ∅. For any fixed p, the metrics d _1p and d _2p are the continuous and uniformly continuous functions, the metric d _3p is the piecewise continuous function almost everywhere on the metric space for any fixed p.

The proposed metric spaces are the new types of spaces that differ from the well-known ones [3]. The general distance d _1p (A, B) is analogues of the Hamming-type distance between objects, which is traditional for many applications. The completely averaged distance d _2p (A, B) characterizes a difference between two objects related to common properties of all objects as a whole. And the locally averaged distance d _3p (A, B) reflects a difference related to properties of only both objects. In the case of sets for p = 1, d ₁₁(A, B) = m(A∆B) is called the Fréchet distance, d ₃₁(A, B) = m(A∆B)/m(A∪B) is called the Steinhaus distance [3].

The measure m(A) of multiset A may be determined in the various ways, for instance, as a linear combination of multiplicity functions: $m\left( \varvec{A} \right) = \sum\nolimits_{s} {w_{s} k_{{\varvec{A}}} (x_{s}^{{e_{s} }} )}$, w _s  > 0. In this case, for example, the Hamming-type distance for p = 1 has the form

$$ \begin{gathered} d_{ 1 1} \left( {\varvec{A},\varvec{B}} \right) = m\left( {\varvec{A}\Delta \varvec{B}} \right) = \sum\limits_{s = 1}^{m} {w_{s} } \sum\limits_{{e_{s} = 1}}^{{h_{s} }} | {\kern 1pt} k_{\varvec{A}} (x_{s}^{{e_{s} }} ) - k_{\varvec{B}} (x_{s}^{{e_{s} }} )|, \hfill \\ \hfill \\ \end{gathered} $$

where w _s  > 0 is a relative importance of the attribute Q _s . Various properties of multisets and multiset metric spaces are considered and discussed in [13].

3 Method of Group Ordering Multi-Attribute Objects

The method ARAMIS (Aggregation and Ranking Alternatives nearby the Multi-attribute Ideal Situations) is developed for group ordering multi-attribute objects that is based on preference aggregation [14, 17]. This method does not require pre-construction of individual rankings objects. Let us represent an object A _i that is described by many repeated quantitative and/or qualitative attributes as a multiset (1). Consider multi-attribute objects A ₁, …, A _n as points of multiset metric space (L(Z), d).

There are two (may be hypothetical) objects with the highest and lowest estimates by all attributes/criteria Q ₁, …, Q _m . These are the best object A ⁺ and the worst object A ⁻, which can be represented as the following multisets in a metric space

$$ \begin{aligned} {\varvec{A}}^{ + } & = \left\{ {k\circ x_{1}^{1} ,0, \ldots ,0,k\circ x_{2}^{1} ,0, \ldots ,0, \ldots ,k\circ x_{m}^{1} ,0, \ldots ,0} \right\}, \\ {\varvec{A}}^{-} & = \{ 0, \ldots ,0,k\circ x_{1}^{{h_{1} }} , \, 0, \ldots ,0,k\circ x_{2}^{{h_{2} }} , \ldots , \, 0, \ldots ,0,k\circ x_{m}^{{h_{m} }} \} , \\ \end{aligned} $$

(3)

where k is a number of experts or instrument techniques. These objects are called also as the ideal and anti-ideal situations or referent points. So, all objects may be arranged with respect to closeness to the best object A ⁺ or the worst object A ⁻ in the multiset metric space (L(Z), d).

The descending arrangement of multi-attribute objects with respect to closeness to the best object A ⁺ is constructed in the following way. An object A _i is said to be more preferable than an object A _j (A _i  ≻ A _j ), if a multiset A _i is closer to the multiset A ⁺ than a multiset A _j , that is d(A ⁺, A _i ) < d(A ⁺, A _j ) in the multiset metric space (L(Z), d). The ascending arrangement of multi-attribute objects with respect to farness to the worst object A ⁻ is constructed analogously. The final ranking multi-attribute objects is constructed as a combination of the descending and ascending arrangements. All objects can be also ordered in accordance with the index $l^{ + } \left( {A_{i} } \right) = d\left( {\varvec{A}^{ + } ,\varvec{A}_{i} } \right)/\left[ {d\left( {\varvec{A}^{ + } ,\varvec{A}_{i} } \right) + d\left( {\varvec{A}^{-} ,\varvec{A}_{i} } \right)} \right]$ of relative closeness to the best object.

4 Method of Group Clustering Multi-Attribute Objects

Cluster analysis is a widely used approach to study the natural grouping large collections of objects and relationships between them. In clustering or classifying multi-attribute objects without a teacher, the association of objects into groups is based on their differences or similarities, which are estimated by a proximity of objects considered as points of attribute space. The principal features of cluster analysis are as follows: the choice of distance between objects in the attribute space; the choice of algorithm for grouping objects; a reasonable interpretation of the formed groups. A selection of the attribute space and the metric type depends on the properties of the analyzed objects. For the objects with manifold attributes, the most adequate is a representation as multisets and use of the metric space (L(Z), d) of measurable multisets with the basic, completely or locally averaged metric.

Traditionally, a cluster is formed as a set-theoretic union of the closest objects [1]. New operations under multisets open new possibilities for aggregation of multi-attribute objects. For example, a group (class) C _t , t = 1, …, g of objects can be obtained as the sum Y _t  = ∑ _i A _i , k _{Y t} (x _j ) = ∑ _i k _{A i} (x _j ), union Y _t  = ∪ _i A _i , k _{Y t} (x _j ) = max _i k _{A i} (x _j ) or intersection Y _t  = ∩ _i A _i , k _{Y t} (x _j ) = min _i k _{A i} (x _j ) of multisets A _i describing the objects, either as a linear combination of multisets Y _t  = ∑ _i b _i  · A _i , Y _t  = ∪ _i b _i  · A _i or Y _t  = ∩ _i b _i  · A _i . When a group C _t of objects is formed by addition of multisets, all of the properties of all objects within a group are aggregated. While forming group C _t of objects by union or intersection of multisets, the best properties (maximal values of attributes) or, respectively, the worst properties (minimal values of attributes) of individual members of a group are strengthened.

In order to generate groups of objects, the following typical approaches are used in clustering techniques: (1) minimize the difference (maximize the similarity) between objects within a group (2) maximize the difference (minimize the similarity) between groups of objects. We assume, for simplicity, that distinctions between objects within the group, between some object and the group of objects, between groups of objects are determined in the same manner and given by one of the above distances d (2).

Consider basic ideas of cluster analysis of multi-attribute objects A ₁,…,A _n represented as multisets A ₁, …, A _n . Hierarchical clustering, when a number of the generated clusters is not defined in advance, consists of the following major stages.

Step 1:

Put g = n, g is the number of clusters, n is the number of objects A _i . Then each cluster C _i consists of a single object A _i , and multisets Y _i  = A _i for all i = 1,…,g.

Step 2:

Calculate the distances d(Y _p , Y _q ) between all possible pairs of multiset represented clusters C _p and C _q for all 1 ≤ p, q ≤ g, p $\neq$ q using one of the metrics d (2).

Step 3:

Find the closest pair of clusters C _u and C _v such that d(Y _u , Y _v ) = min _p,q d(Y _p , Y _q ), and form a new cluster C _r , which represented as a sum Y _r  = Y _u  + Y _v , union Y _r  = Y _u ∪Y _v , intersection Y _r  = Y _u ∩Y _v of correspondent multisets or a linear combination of one of these operations.

Step 4:

Reduce the number of clusters per unit: g = n − 1. If g = 1, then output the result and stop. If g > 1, then go to Step 5.

Step 5:

Calculate the distances d(Y _p ,Y _r ) between pairs of new multisets represented clusters C _p and C _r for all 1 ≤ p, r ≤ g, p $\neq$ r. Go to Step 3.

The algorithm builds a hierarchical tree or dendrogram by a successive aggregation of objects into groups. New objects/clusters C _p and C _q appear, while moving from the root of the tree by its branches, going at each step in one of the closest clusters C _r . The process of hierarchical clustering ends when all the objects are grouped into several classes or a single class. The procedure can also be interrupted at some stage in accordance with any rule, for instance, when the difference index exceeds the given threshold level [11].

The nature of cluster formation and results are largely depended on the type of used metric. The basic metric d ₁₁ and completely averaged metric d ₂₁ give almost identical results. In the process of clustering, ‘small’ objects (with small numbers of attributes) are merged firstly, and more ‘large’ objects are aggregated later. The resulted groups are comparable to the number of included objects, but very differ from each other by sets of characterizing attributes. The clustering with locally averaged metric d ₃₁ starts from combining similar objects of ‘medium’ and ‘large’ sizes with significant ‘common’ sets of attributes. Different ‘small’ objects are joined later. The final grouping objects obtained in the first and second cases can be strongly varied.

In the methods of non-hierarchical cluster analysis, the number of clusters is considered as fixed and specified in advance. For multi-attribute objects described by multisets, a generalized framework of nonhierarchical clustering includes the following stages.

Step 1:

Select an initial partition of collection A ₁, …, A _n of n objects in g clusters C ₁, …, C _g .

Step 2:

Distribute all of the objects A ₁, …, A _n by clusters C ₁, …, C _g according to some rule. For example, calculate the distances d(A _i , Y _t ) between multisets A _i (i = 1, …, n) represented objects A _i and multisets Y _t represented clusters C _t (t = 1, …, g). Place the object A _i in the nearest cluster C _h with the distance d(A _i , Y _h ) = min _t d(A _i , Y _t ). Or determine the center $A_{t}^\circ$ of each cluster C _t , for instance, by solving the optimization task $J(\varvec{A}_{t}^\circ ,\varvec{Y}_{t} )$ $= { \hbox{min} }_{p} \sum\nolimits_{i} d \left( {\varvec{A}_{i} ,\varvec{A}_{p} } \right)$. Place each object A _i in the cluster C _r with the nearest center $A_{r}^\circ$ given by the condition $d(\varvec{A}_{i} ,\varvec{A}_{r}^\circ ) = { \hbox{min} }_{t} d(\varvec{A}_{i} ,\varvec{A}_{t}^\circ )$. The center $\varvec{A}_{t}^\circ$ of cluster C _t can coincide with one of the really existing objects A _i or be a so-called ‘phantom’ object that is absent in the original collection of objects but constructed as multiset.

Step 3:

If all objects A ₁, …, A _n do not change their cluster membership that was given by the initial partition in clusters C ₁, …, C _g , then output the result and stop. Otherwise return to Step 2.

The results of object classification can be estimated by a quality of the partition. The best partition can be found, in particular, as a solution of the following optimization problem: $\sum\nolimits_{t} J (\varvec{A}_{t}^\circ ,\varvec{Y}_{t} ) \to$min, where the functional $J(\varvec{A}_{t}^\circ ,\varvec{Y}_{t} )$ is defined above. In general, the solution of optimization problem is ambiguous since the functional H(Y _opt) is a function with many local extrema. The final result depends also on the initial (near or far from optimal) allocation of objects into classes.

Often in clustering procedures, a maximization of various indicators of objects’ similarity is used instead of a minimization of distance between objects that characterizes their differences. The following indexes of objects’ similarity can be introduced

$$\begin{aligned}s_{1} \left({\varvec{A}}, {\varvec{B}} \right) & = 1 - m\left( {\varvec{A}}\Delta {\varvec{B}} \right)/m\left( {\varvec{Z}} \right), s_{2} \left( {\varvec{A}},{\varvec{B}} \right) = m({\varvec{A}} \cap {\varvec{B}})/m\left( {\varvec{Z}} \right), \\ s_{3} \left( {\varvec{A}}, {\varvec{B}} \right) & = m({\varvec{A}} \cap {\varvec{B}})/m({\varvec{A}} \cup {\varvec{B}}). \\ \end{aligned}$$

In the case of multisets, the functions s ₁, s ₂, s ₃ generalize the known indexes of similarity such as, respectively, the simple matching coefficient, Russell-Rao measure of similarity, Jaccard coefficient or Rogers-Tanimoto measure [1]. The simple matching coefficient s ₁ and Russell-Rao measure s ₂ of similarity are connected with the expression s ₁(A, B) = s ₂(A, B) + s ₂(A, B), which is one of the possible binary decompositions of maximal multiset Z on blocks of coverings and overlapping multisets [12].

5 Method of Group Sorting Multi-Attribute Objects

Consider a problem of group classification of multi-attribute objects with teachers as follows. Several experts evaluate each object from the collection A ₁, …, A _n upon all criteria Q ₁, …, Q _m and make a recommendation r _t for sorting the object into one of the classes C _t , t = 1,…,g. Need to find a simple general group rule, which aggregates a large family of inconsistent individual expert-sorting rules and assigns objects to the given classes taking into account inconsistent opinions.

The method MASKA (abbreviation of the Russian words Multi-Attribute Consistent Classification of Alternatives) is used for group sorting multi-attribute objects [14–16]. An object A _i with a multiple criteria estimates $X_{s} = \{ x_{s}^{{e_{s} }} \}$, s = 1, …, m may be represented as the following multiset of the type (1)

$$ \begin{aligned} {\varvec{A}}_{i} &= \{ k_{{\varvec{A}}i} \left( {x_{1}^{1} } \right)\circ x_{1}^{1} , \ldots ,k_{{\varvec{A}}i} (x_{1}^{{h_{1} }} )\circ x_{1}^{{h_{1} }} , \ldots , \hfill \\ & \qquad \quad k_{{\varvec{A}}i} \left( {x_{m}^{1} } \right)\circ x_{m}^{1} , \ldots ,k_{{\varvec{A}}i} (x_{m}^{{h_{m} }} )\circ x_{m}^{{h_{m} }} ,k_{{\varvec{A}}i} \left( {r_{1} } \right)\circ r_{1} , \ldots ,k_{{\varvec{A}}i} \left( {r_{f} } \right)\circ r_{g} \} , \hfill \\ \end{aligned} $$

(4)

which is drawn from the domain P = X ₁∪…∪X _m ∪R = X∪R. The part of sorting attributes R = {r ₁,…,r _g } is the set of expert recommendations. Here $k_{{\varvec{A}}i} (x_{s}^{{e_{s} }} )$ and k _{A i} (r _t ) are equal to numbers of experts who gives the estimate $x_{s}^{{e_{s} }}$ and the recommendation r _t to the object A _i . Obviously, judgments of many experts may be similar, diverse, or contradictory. These inconsistencies express subjective preferences of individual experts and cannot be considered as accidental errors.

The representation (4) of object A _i can be written as a collective sorting rule

$$ {\text{IF}}\left\langle {\text{conditions}} \right\rangle ,{\text{ THEN}}{\kern 1pt} \left\langle {\text{decision}} \right\rangle , $$

which is associated with arguments in the formula (4) as follows. The antecedent term 〈conditions〉 includes the various combinations of criteria estimates $x_{s}^{{e_{s} }}$, which describes the object features. The consequent term 〈decision〉 denotes that the object A _i belongs to the class C _t , if some conditions are fulfilled. The object A _i is assigned to the class C _t in accordance with the rule of voices majority that is, for instance, the relative majority if k _{A i} (r _t ) > k _{A i} (r _p ) for all p $\neq$ t, or the absolute majority if $k_{\user2{A}i} (r_{t})\,>\,\sum_{p\,\neq\,t} k_{\user2{A}i} (r_{p})$.

In order to simplify the problem, let us assume that the collection of objects A ₁, …, A _n is to be sorted only into two classes C _a (say, more preferable) and C _b (less preferable) that is g = 2. This demand is not the principle restriction. Whenever objects are to be sorted into more than two classes, it is possible to divide the object collection into two classes, then into subclasses, and so on. For instance, competitive projects may be classified as projects approved and not approved, then the not approved projects may be sorted as projects rejected and considered later, and so on.

Let us correspond to each class C _a and C _b multisets Y _a and Y _b , which are formed as sums of multisets represented multi-attribute objects. In this case,

$$ \begin{aligned} \varvec{Y}_{t} &= \{ k_{{\varvec{Y}}t} \left( {x_{1}^{1} } \right)\circ x_{1}^{1} , \ldots ,k_{{\varvec{Y}}t} (x_{1}^{{h_{1} }} )\circ x_{1}^{{h_{1} }} , \ldots , \hfill \\ &\quad \quad \quad k_{{\varvec{Y}}t} \left( {x_{m}^{1} } \right)\circ x_{m}^{1} , \ldots ,k_{{\varvec{Y}}t} (x_{m}^{{h_{m} }})\circ x_{m}^{{h_{m} }} ,k_{{\varvec{Y}}t} \left( {r_{a} } \right)\circ r_{a} ,k_{{\varvec{Y}}t} \left( {r_{b} } \right)\circ r_{b} \} , \hfill \\ \end{aligned} $$

where $k_{{{\varvec{Y}}t}} (x_{s}^{{e_{s} }} ) = \sum\nolimits_{i \in It} {k_{{\varvec{A}i}} (x_{s}^{{e_{s} }} )} ,k_{{\varvec{Y}t}} \left( {r_{t} } \right) = \sum\nolimits_{i \in It} {k_{{\varvec{A}i}} \left( {r_{t} } \right)}$, t = a, b, the index subsets I _a ∪I _b  = {1, …, n}, I _a ∩I _b  = ∅. The above expression represents the collective decision rule of all experts for sorting multi-attribute objects to the class C _t .

The problem of object classification may be considered as the problem of sorting multisets in a metric space (L(Z), d). The main idea of aggregating a large family of discordant individual expert-sorting rules in a generalized group decision rule is formulated as follows. Let us introduce a set of new attributes Y = {y _a , y _b }, which elements related to the classes C _a and C _b , and construct the following new multisets

$$ \begin{aligned} R_{a} & = \{ k_{{\varvec{R}}a} \left( {y_{a} } \right)\circ y_{a} ,k_{{\varvec{R}}a} \left( {y_{b} } \right)\circ y_{b} \} ,R_{b} = \{ k_{{\varvec{R}}b} \left( {y_{a} } \right)\circ y_{a} ,k_{{\varvec{R}}b} \left( {y_{b} } \right)\circ y_{b} \} , \\ Q_{j} & = \{ k_{{\varvec{Q}}j} \left( {y_{a} } \right)\circ y_{a} ,k_{{\varvec{Q}}j} \left( {y_{b} } \right)\circ y_{b} \} \\ \end{aligned} $$

drawn from the set Y. Here k _{R a} (y _t ) = k _{Y t} (r _a ), k _{R b} (y _t ) = k _{Y t} (r _b ), $k_{{\varvec{Q}j}} \left( {y_{t} } \right) = k_{{\varvec{Y}t}} (x_{s}^{j} )$, j = 1, …, h _s . We shall call the multisets R _a , R _b as ‘categorical’ and the multisets Q _j as ‘substantial’ multisets.

Note that the distance d(R _a , R _b ) between multisets R _a and R _b is the maximal distance between objects belonging to the different classes C _a and C _b . So, the categorical multisets R _a and R _b correspond to the best binary decomposition of the objects collection into the given classes C _a and C _b according to primary sorting rules of experts

$$ \begin{gathered} {\text{IF}}\left\langle {\left( {k_{{\varvec{A}}i} \left( {r_{a} } \right) > k_{{\varvec{A}}i} \left( {r_{b} } \right)} \right)} \right\rangle ,{\text{ THEN}}\left\langle {{\text{Object}}\,A_{i} \in C_{a} } \right\rangle , \hfill \\ {\text{IF}}\left\langle {\left( {k_{{\varvec{A}}i} \left( {r_{a} } \right) < k_{{\varvec{A}}i} \left( {r_{b} } \right)} \right)} \right\rangle ,{\text{ THEN}}\left\langle {{\text{Object}}\,A_{i} \in C_{b} } \right\rangle . \hfill \\ \end{gathered} $$

(5)

Thus, it is necessary to construct a pair of new substantial multisets $\varvec{Q}_{sa}{^{*}}$ and $\varvec{Q}_{sb}{^{*}}$ for every attribute group Q _s , s = 1, …, m such that these multisets as points of multiset metric space are to be placed at the maximal distance. The multisets Q _sa and Q _sb aggregate groups of multisets Q _j as the sums: Q _sa  = ∑ _j∈Jsa Q _j , Q _sb  = ∑ _j∈Jsb Q _j , where the index subsets J _sa ∪J _sb  = {1, …, h _s }, J _sa ∩J _sb  = ∅. The substantial multisets $\varvec{Q}_{sa}{^{*}}$ and $\varvec{Q}_{sb}{^{*}}$, which correspond to the best binary decomposition of objects for the s-th attribute Q _s and are the mostly coincident with primary expert-sorting objects into the given classes C _a and C _b , are a solution of the following optimization problem:

$$ d\left( {{\varvec{Q}}_{sa} ,{\varvec{Q}}_{sb} } \right) \to \hbox{max} d\left( {{\varvec{Q}}_{sa} ,{\varvec{Q}}_{sb} } \right) \, = d\left( {{\varvec{Q}}_{sa}{^{*}},{\varvec{Q}}_{sb}{^{*}}} \right). $$

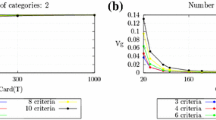
The set of attributes Q ₁, …, Q _m can be ranged by the value of distance $d\left( {\varvec{Q}_{sa}{^{*}},\varvec{Q}_{sb}{^{*}}} \right)$ or the level of approximation rate $V_{s} = d\left( {\varvec{Q}_{sa}{^{*}},\varvec{Q}_{sb}{^{*}}} \right)/d\left( {\varvec{R}_{a} ,\varvec{R}_{b} } \right)$. We shall call an attribute value $x_{s}^{j} \in \varvec{Q}_{st}{^{*}}$, j∈J _st , t = a, b that characterizes the class C _t as a classifying attribute for the correspondent class. The classifying attribute that provides the acceptable level of approximation rate V _s  ≥ V ₀ is to be included in the generalized decision rule for group multicriteria sorting objects. The level of approximation rate V _s shows a relative significance of the s-th property Q _s within the generalized decision rule.

Various combinations of the classifying attributes produce the generalized decision rules for group sorting objects into the classes C _a and C _b as follows

$$ \begin{aligned} {\text{IF}}\left\langle {(x_{u}^{j} \in {\varvec{Q}}_{ua}{^{*}}){\text{ AND }}(x_{v}^{j} \in {\varvec{Q}}_{va}{^{*}}){\text{ AND}} \ldots {\text{AND }}(x_{w}^{j} \in {\varvec{Q}}_{wa}{^{*}})} \right\rangle , \hfill \\ \quad \quad \quad \quad \quad \quad \quad {\text{THEN}}\left\langle {{\text{Object}}\,A_{i} \in C_{a} } \right\rangle , \hfill \\ \end{aligned} $$

(6)

$$ \begin{aligned} {\text{IF}}\left\langle {(x_{u}^{j} \in {\varvec{Q}}_{ub}{^{*}}){\text{ AND }}(x_{v}^{j} \in {\varvec{Q}}_{vb}{^{*}}){\text{ AND}} \ldots {\text{AND }}(x_{\,w}^{j} \in {\varvec{Q}}_{wb}{^{*}}),} \right\rangle \hfill \\ \quad \quad \quad \quad \quad \quad \quad {\text{THEN}}\left\langle {{\text{Object}}\,A_{i} \in C_{b} } \right\rangle . \hfill \\ \end{aligned} $$

(7)

Remark, generally, that these generalized group decision rules are quite different.

Among the objects, which have been assigned to the given class C _a or C _b in accordance with the generalized decision rule (6) or (7), there are the correctly and not correctly classified objects. So, a construction of collective decision rules for sorting multi-attribute objects, which aggregate a large number of inconsistent individual expert-sorting rules, includes not only a selection of the classifying attributes $x_{s}^{j} \in Q_{sa}{^{*}},x_{s}^{j} \in Q_{sb}{^{*}}$, but also a determination of the correctly and contradictory classified objects.

Let us find such attribute values that maximize numbers N _a and N _b of the correctly classified objects, and minimize numbers N _ac and N _bc of the not correctly classified objects. We can find, step by step, a single criterion $Q_{ua}{^{*}}$, then a couple of criteria $Q_{ua}{^{*}}$ and $Q_{va}{^{*}}$, three criteria $Q_{ua}{^{*}},Q_{va}{^{*}},Q_{wa}{^{*}}$, four criteria and so on, which are included in the generalized decision rules (6) or (7), and provide the minimal difference N _a − N _ac or N _b − N _bc . Finally, we obtain the aggregated decision rules for consistent sorting the objects

$$ \begin{gathered} \quad {\text{IF}}\left\langle {\left( {\sum\nolimits_{x \in {\varvec{Q}}ua{^{*}}} {k_{{\varvec{A}i}} } \left( x \right) > \sum\nolimits_{x \in {\varvec{Q}}ub{^{*}}} {k_{{\varvec{A}i}} } \left( x \right)} \right){\text{ AND }}} \right. \hfill \\ \quad \quad \left( {\sum\nolimits_{x \in {\varvec{Q}}va{^{*}}} {k_{{\varvec{A}i}} } \left( x \right) > \sum\nolimits_{x \in {\varvec{Q}}vb{^{*}}} {k_{{\varvec{A}i}} } \left( x \right)} \right){\text{ AND}} \ldots \hfill \\ \left. {{\text{AND }}\left( {k_{{\varvec{A}i}} \left( {r_{a} } \right) > k_{{\varvec{A}i}} \left( {r_{b} } \right)} \right)} \right\rangle ,{\text{ THEN}}\left\langle {{\text{Object}}\,A_{i} \in C_{a} \backslash C_{ac} } \right\rangle , \hfill \\ \end{gathered} $$

(8)

$$ \begin{gathered} \quad {\text{IF}}\left\langle {\left( {\sum\nolimits_{x \in {\varvec{Q}}ua{^{*}}} {k_{{\varvec{A}i}} } \left( x \right) < \sum\nolimits_{x \in {\varvec{Q}}ub{^{*}}} {k_{{\varvec{A}i}} } \left( x \right)} \right){\text{ AND}}} \right. \, \hfill \\ \quad \quad \left( {\sum\nolimits_{x \in {\varvec{Q}}va{^{*}}} {k_{{\varvec{A}i}} } \left( x \right) < \sum\nolimits_{x \in {\varvec{Q}}vb{^{*}}} {k_{{\varvec{A}i}} } \left( x \right)} \right){\text{ AND}} \ldots \hfill \\ \left. {{\text{AND }}\left( {k_{{\varvec{A}i}} \left( {r_{a} } \right) < k_{{\varvec{A}i}} \left( {r_{b} } \right)} \right)} \right\rangle ,{\text{ THEN}}\left\langle {{\text{Object}}{\kern 1pt} A_{i} \in C_{b} \backslash C_{bc} } \right\rangle . \hfill \\ \end{gathered} $$

(9)

These aggregated decision rules define the specified classes C _a \C _ac (say, completely preferable) and C _b \C _bc (completely not preferable) of the correctly classified objects. These aggregated rules for consistent sorting approximate the family of initial sorting rules of many individual experts.

Simultaneously the specified class C _c  = C _ac ∪C _bc of the contradictory classified objects is built. Such objects satisfy the aggregated decision rule for inconsistent sorting

$$ \begin{aligned} & \quad \quad \quad {\text{IF}}\left\langle {\left[ {\left( {\sum\nolimits_{x \in {\varvec{Q}}ua{^{*}}} {k_{{\varvec{A}}i} } \left( x \right) > \sum\nolimits_{x \in {\varvec{Q}}ub{^{*}}} {k_{{\varvec{A}}i} } \left( x \right)} \right){\text{ AND}}} \right. \, } \right. \\ & \quad \quad \quad \quad \left( {\sum\nolimits_{x \in {\varvec{Q}}va{^{*}}} {k_{{\varvec{A}}i} } \left( x \right) > \sum\nolimits_{x \in {\varvec{Q}}vb{^{*}}} {k_{{\varvec{A}}i} } \left( x \right)} \right){\text{AND}} \ldots \\ & {\text{AND }}\left( {k_{{\varvec{A}}i} \left( {r_{a} } \right) < k_{{\varvec{A}}i} \left( {r_{b} } \right)} \right)\left] {\text{ OR }} \right[\left( {\sum\nolimits_{x \in {\varvec{Q}}ua{^{*}}} {k_{{\varvec{A}}i} } \left( x \right) < \sum\nolimits_{x \in {\varvec{Q}}ub{^{*}}} {k_{{\varvec{A}}i} } \left( x \right)} \right){\text{ AND }} \\ & \quad \quad \quad \quad \left( {\sum\nolimits_{x \in {\varvec{Q}}va{^{*}}} {k_{{\varvec{A}}i} } \left( x \right) < \sum\nolimits_{x \in {\varvec{Q}}vb{^{*}}} {k_{{\varvec{A}}i} } \left( x \right)} \right){\text{ AND}} \ldots \\ & \left. {\quad {\text{AND }}\left( {k_{{\varvec{A}}i} \left( {r_{a} } \right) > k_{{\varvec{A}}i} \left( {r_{b} } \right)} \right)} \right],{\text{ THEN}}\left\langle {\text{Object}\,A_{i} \in C_{c} } \right\rangle . \\ \end{aligned} $$

(10)

This aggregated rule helps a DM to discover possible inconsistencies of individual expert rules and analyze additionally the contradictory classified objects.

6 Case Studies: Multiple-Criteria Expertise of R&D Projects

The developed techniques were applied to real-life expertise of R&D projects in the Russian Foundation for Basic Research (RFBR). RFBR is the Federal agency that organizes and funds basic research, and exams their practical applications. In RFBR, there is the special peer review system for a selection of the applications and assessment of the completed projects—the original multi-expert and multi-criteria expertise, similar to that found nowhere else in the world.

Several independent experts estimated each project using special questionnaires, which include specific qualitative criteria with detailed verbal rating scales. Additionally, experts give the recommendations on whether to support the application (at the competition stage) or to continue the project (at the intermediate stage). Experts estimate the scientific and practical values of the obtained results (at the final stage when the project is ended). On the basis of expert judgments, the Expert Board of RFBR decides to approve or reject the new project, to continue the project implementation, and evaluates the efficiency of the completed project. Finally, the Expert Board of RFBR determines the size of financing the supported project.

The most of methodologies, which are applied for expert estimation in different areas, uses quantitative approaches that are based on a numerical measurement of object characteristics. However, such approaches are not suitable for the expertise in RFBR, where projects are evaluated by several experts on many qualitative criteria with verbal scales.

To select the best competitive applications, the Expert Board of RFBR is need in a simple collective decision rules, which aggregate many contradictory decision rules of individual experts described with non-numerical data. These aggregated decision rules for sorting applications have been constructed by the MASKA method, and could not been found with other known MCDM techniques.

During the RFBR expertise of the goal-oriented R&D projects, several experts (usually, three) evaluate the applications upon 11 qualitative criteria presented in the expert questionnaire. These criteria are combined in two groups such as ‘Scientific characteristics of the project’ and ‘Evaluation of possibilities for the practical implementation of the project’. The first group includes 9 criteria. These are as follows: Q ₁. Fundamental level of the project; Q ₂. Directions of the project results; Q ₃. Goals of research; Q ₄. Methods of achievement of the project goals; Q ₅. Character of research; Q ₆. Scientific value of the project; Q ₇. Novelty of the proposed solutions; Q ₈. Potential of the project team; Q ₉. Technical equipment for the project realization. The second group consists of 2 criteria: Q ₁₀. Completion stage of basic research suggested in the project, and Q ₁₁. Applicability scope of the research results.

Each criterion has nominal or ordered scale with verbal grades. For instance, the scale X ₇ of the criterion Q ₇. ‘Novelty of the proposed solutions’ looks as follows; $x_{ 7}^{ 1}$—the solutions were formulated originally and are undoubtedly superior to the other existing solutions; $x_{ 7}^{ 2}$—the solutions are on the same level as other existing solutions; $x_{ 7}^{ 3}$—the solutions are inferior to some other existing solutions.

Additionally, every expert gives a recommendation on the feasibility of the project support using the following scale: r ₁—unconditional support (grade ‘5’), r ₂—recommended support (grade ‘4’), r ₃—possible support (grade ‘3’), r ₄—should not be supported (grade ‘2’).

The proposed approach to a competitive selection of the goal-oriented R&D projects has been tested on the real database. This base included the expert evaluations of the supported and rejected applications in the following fields: ‘Physics and astronomy’ (totally 127 projects, including 39 supported and 88 rejected applications); ‘Biology and medical science’ (totally 252 projects including 68 supported and 184 rejected applications).

Expert data was processed with the MASKA method. As a result in the fields mentioned above, it was sufficient to use combinations of only several criteria, namely Q ₆, Q ₁₀, and Q ₁₁, in order to construct the aggregated collective decision rule for the unconditional support of project. So, this decision rule had the following form:

$$ \begin{aligned} & \text{IF}\left\langle {\text{Object}\,A_{i}\,\text{is estimated with the criteria grades} \, \left( {x_{6}^{1} \,\text{or}\,x_{6}^{2} } \right),} \right. \\ & \left. {\quad \quad \quad \quad \text{AND} \, \left( {x_{10}^{1} \,{\text{or}}\,x_{10}^{2} } \right),\text{AND} \, \left( {x_{11}^{1} \,{\text{or}}\,x_{11}^{2} } \right)} \right\rangle , \\ & \quad \quad \quad \quad \quad \quad \text{THEN}\left\langle {\text{Object}\,A_{i} \in C_{a} \backslash C_{ac} } \right\rangle . \\ \end{aligned} $$

The aggregated rule for the project support can be rewritten with a natural language as follows: “The project is unconditionally supported if the project has the exceptional or very high value of scientific significance; basic research suggested in the project are completed in the form of a laboratory prototype or key elements of development; and the project has a large or interdisciplinary applicability scope of the research results”.

To evaluate efficiency of the goal-oriented R&D projects, we used the methodology of group verbal decision analysis in the reduced attribute space. At the first stage, the complex criterion of project efficiency is constructed with the original interactive procedure HISCRA (HIerarchical Structuring CRiteria and Attributes) for reducing the dimension of attribute space [18]. A construction of complex criterion scale is considered as the ordinal classification problem, where the classified alternatives are combinations of verbal grades of criteria scales. The decision classes are verbal grades of the complex criteria. At the second stage, grades of the complex criteria are composed, step by step, by using various verbal decision methods [10]. Thus, each project is assigned into some class correspondent to the grade of complex criterion, which are obtained with different methods. At the third stage, all projects are ordered by the ARAMIS method [14, 17]. The hierarchical aggregation of initial attributes allows to generate manifold collections of complex criteria, find the most preferable solution, and diminish essentially time that a DM spends for solving a problem.

During the RFBR expertise of the completed goal-oriented R&D projects, several experts (usually, two, three or four) evaluate the obtained results upon 8 qualitative criteria presented in the expert questionnaire. These criteria are as follows: Q ₁. Degree of the problem solution; Q ₂. Scientific level of results; Q ₃. Appropriateness of patenting results; Q ₄. Prospective application of results; Q ₅. Result correspondence to the project goal; Q ₆. Achievement of the project goal; Q ₇. Difficulties of the project performance; Q ₈. Interaction with potential users of results.

Each criterion has two or three-point scale of ordered verbal grades. For example, the scale X ₁ of the criterion Q ₁. ‘Degree of the problem solution’ looks as follows: $x_{ 1}^{ 1}$—the problem is solved completely, $x_{ 1}^{ 2}$—the problem is solved partially, $x_{ 1}^{ 3}$—the problem is not solved. The criterion Q ₆. ‘Achievement of the project goal’ is rated as $x_{ 6}^{ 1}$—really, $x_{ 6}^{ 2}$—non-really.

The rates of project efficiency correspond to the ordered grades on a scale of the top level complex criterion D. ‘Project efficiency’ as d ¹—superior, d ²—high, d ³—average, d ⁴—low, d ⁵—unsatisfactory. These grades, which were considered as the new attributes that characterize the projects, was formed with four different combinations of verbal decision methods.

The real database included expert assessments of results of goal-oriented R&D projects, which had been completed in the following fields: ‘Mathematics, Mechanics and Computer Science’ (totally 48 projects), ‘Chemistry’ (totally 54 projects), ‘Information and telecommunication resources’ (totally 21 projects). For instance, the obtained final ranking projects on Mathematics, Mechanics and Computer Science in accordance with the index l ⁺(A _i ) of relative closeness to the best object is as follows: 23 projects have the superior level of efficiency (l ⁺(A _i ) = 0,333), 1 project has the level of efficiency between superior and high (l ⁺(A _i ) = 0,429), 24 projects have the high level of complex efficiency (l ⁺(A _i ) = 0,500).

7 Conclusion

In this chapter, we considered the new tools for group ordering and sorting objects described with many numerical, symbolic and/or verbal attributes, when several copies of object may exist. These techniques are based on the theory of multiset metric spaces. Underline that verbal attributes in these methods are not transformed in or replaced by any numerical ones as, for instance, in MAUT and TOPSIS methods [6], and in fuzzy set theory [21].

The multiset approach allows us to solve traditional MCDM problems in more simple and constructive manner, and discover new types of problems never being sold earlier, while taking into account inconsistencies of objects’ features and preference contradictions of many actors. The ARAMIS technique is simpler and easier than the other well-known approaches to ranking multiple criteria alternatives. The MASKA technique is the unique method for group classification of multi-attribute objects and has no analogues.