Introduction to Streaming Complex Plasmas B: Theoretical Description of Wake Effects

Abstract

A key problem in the description of non-ideal, multi-component plasmas is the drastic difference in the characteristic length and time scales of the different particle species. This challenging multiscale problem inherent to studying streaming complex plasmas can efficiently be tackled by a statistical ansatz for the light plasma constituents in combination with first-principle Langevin dynamics simulations of the heavy and strongly correlated dust component. Of crucial importance in this scheme is the quality of the dynamically screened Coulomb potential. For this purpose, we introduce Kielstream, a new high-performance computer code for the computation of three-dimensional plasma wakefields and the resulting electric fields. The optimization techniques used and the handling of competing numerical errors are discussed in detail. Results are presented for the wakefield around a single dust grain as well as multiscale simulations of a correlated ensemble of grains revealing fundamental structural changes when wake effects take charge.

This chapter is dedicated to Glenn R. Joyce (June 24, 1939—December 4, 2011)

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Non-equilibrium processes can generate intriguing, counterintuitive many-particle phenomena such as the attraction between like charged particles as we have seen in the previous chapter. Indeed, our whole non-static universe consists to a great extent of matter in a non-equilibrium plasma state. The theoretical description of non-ideal plasmas in non-equilibrium is, however, very challenging. For the sake of simplification non-equilibrium and streaming effects are often neglected. In this chapter we present a multiscale concept that adequately incorporates the interplay of streaming ions, electrons, neutral atoms, and strongly coupled dust grains.

Table 3.1 Typical parameters of a multi-component complex plasma (argon ions, singly charged)

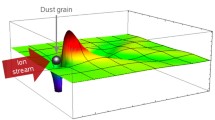
Streaming effects are often connected to a fascinating wave phenomenon: the creation of wakefields. This collective dynamical effect is probably best known from the V-shaped wake pattern behind objects (ships, dugs, etc.) moving on a calm water surface. As it was demonstrated in the previous chapter, similar wake effects also do exist in complex plasmas—a heterogeneous composition of electrons, ions, neutral atoms, and highly charged micrometer-sized “dust-grains”, see Table 3.1. Remarkably enough, plasma wakes can even be made visible. It is reported that when an additonal object, a ‘cm’-sized massive projectile is placed in a dusty plasma chamber, the dust grains arrange themselves within the ion wakefield of the projectile and make it visible to the naked eye (see sketch in Fig. 3.1).

The most remarkable wake effect is, however, found at a smaller scale when sub-nm-sized ions are streaming against the much heavier (and thus much more inert) dust grains. Here, the wakefield gives rise to an effective attractive interaction between like-charged micro dust particles that in the static case strongly repel each other.

2 Simulation Approaches to Streaming Multi-Component Plasmas

Highly charged polymer micro-spheres carrying about ten thousand electron charges are giving rise to the strongest correlations known in nature—even at room temperature conditions [1]. Therefore, complex (dusty) plasmas are readily used as a reference system allowing for a precise study of collective dynamical and structural properties of the strongly correlated dust component under the influence of the partially ionized plasma background. The results are of direct relevance for other type of plasmas, e.g., for dense plasmas (also called “warm dense matter”) where the impact of streaming effects on the mutual interplay of quantum degenerate electrons, classical ions and neutral atoms has recently become of larger interest [2, 3].

An accurate theoretical description of a partially ionized complex plasma raises a big challenge. In order to achieve a basic theoretical understanding of streaming effects and the fundamental interactions leading to collective behavior, we have to deal with the correlated dynamics of a non-ideal, partially ionized multi-component plasma in a non-equilibrium streaming situation.

Fig. 3.1

Chalkboard sketch of a macroscopically large plasma wake which is created by fast ions streaming around a $1$ cm sized projectile (which is attached to a string). The wake becomes visible to the naked eye when micrometer sized dust grains are added, which populate the 3D wake structure. Unfortunately, no picture of this experiment is known to exist. Drawing by Murillo [4]

Table 3.1 reveals that the main issue in the description of a real plasma lies in the huge mass asymmetry of the different particle species which leads to drastic differences in the relevant space and time scales which must be adequately taken into account. A dust-to-ion mass ratio of about $10^{13}$ results in a time scale gap of five orders of magnitude that makes selfconsistent simulations numerically utmost expensive. Even worse, in order to capture collective dynamical effects long time series of up to several tens of seconds must be captured.

In dusty plasma physics there are two complementary approaches which help us to overcome these numeric limitations: (i) large-scale particle-in-cell (PIC) simulations, and (ii) hybrid molecular dynamics (MD) simulations based on the dynamical screening approach . Both approaches have turned out to be very powerful in the kinetic simulation of plasma streaming and wake effects.

2.1 Particle-in-Cell Simulations of Plasma Wakes

Kinetic particle simulations such as the PIC method have proven to be the most efficient way of solving the Vlasov equation for arbitrary particle distributions in classical plasmas, e.g. Refs. [5–8]. To take into account short range collisions (beyond the Vlasov mean field), often a Monte Carlo collision module is added (PIC-MCC). Large-scale PIC simulations allow for an accurate description of ion-streaming effects including nonlinear phenomena and have been mostly applied to study a single dust grain or two in a complex plasma and occasionally larger systems. Furthermore PIC simulations allow for a selfconsistent description of the grain charging process.

While PIC is close to a first-principle description, in case of a complex plasma it faces severe limitations and difficulties. The mentioned huge mass asymmetry of dust grains and ions causes a many order of magnitude difference of characteristic time scales, see Table 3.1. Therefore, it is practically impossible to resolve the ionic dynamics and the dust dynamics simultaneously, i.e., with the PIC method the dust can only be treated statically. In particular for subsonic plasma conditions, $M<1$, PIC simulations suffer serious convergence problems due to substantial numerical noise even for (insufficient) low grid-resolutions. In order to reduce this issue, often relatively large grain sizes (giving rise to large grain charges) are considered which, however, typically exaggerate the contribution of nonlinearities.

Therefore, for studying many-body effects in complex plasmas, in particular, to analyse the dust particle dynamics and compare to experimental single-particle trajectories, this method is presently not suitable. The alternative is the multi-scale dynamical screening approach which allows us to essentially extend the simulation time to the scale of the dust dynamics. PIC simulations (where they are available) will be used to carefully test and benchmark the linear response based simulation results.

2.2 Multiscale Approach to the Dynamics of Complex Plasmas

The challenging multi-scale problem addressed above can be effectively reduced by the dynamical screening approach which enables us to directly include the focussing effect of a dust grain on streaming ions by means of an effective plasma-mediated dust potential derived from plasma kinetic theory, (see Fig. 3.2) [2, 9–13].¹ The statistical description of the lighter plasma constituents on the basis of a dynamic dielectric response function allows for an accurate description of essential equilibrium and non-equilibrium plasma properties including screening, wakefield oscillations, ion and electron thermal effects as well as ion-neutral collisions and Landau damping [11, 14].

In the considered multiscale approach, the strong Coulomb correlations of the highly negatively charged dust component are treated exactly on first-principles by classical Langevin molecular dynamics (LMD) simulations. This allows us to analyse the dynamics of individual dust grains on a kinetic level with very high precision. The damping effect of neutrals on the grain dynamics, i.e., dust-neutral collisional effects, is taken into account by a Langevin-Fokker-Planck approximation.

The multiscale simulation approach consists basically of two parts:

Part I:

Computation of the electrostatic potential around a single grain (Fig. 3.2) from the dynamic dielectric function in a linear response approximation. The plasma-mediated potential represents an effective dust–dust Coulomb interaction which is dynamically screened by streaming ions.

Part II:

Use of these wake potentials in $N$-particle LMD simulations that yield the “exact” trajectory of each particle in the classical phase space [23].

The $N$-particle dust dynamics simulations will allow us to study the real dynamics of finite or extended dust ensembles, their self-organised structure formation as well as wake-field driven phase transitions with high numerical resolution and without having to numerically resolve the fast plasma time scales.

The results depend on three dimensionless simulation input parameters: (i) the Mach number$M = |\mathbf{{u}}_i| / c_s$ defined as the the ratio of ion drift velocity to the sound velocity $c_s=(k_B T_e/m_i)^{1/2}$, (ii) the electron-to-ion temperature ratio $T_r=T_e/T_i$, and (iii) the ion collision frequency $\nu _{i}$ which is directly proportional to the neutral gas pressure [6].

2.2.1 Effective Dust–Dust Interaction

The main idea of the dynamical screening approach is to retain the first-principle character of MD simulations for the dust particles and, at the same time, to turn the huge mass asymmetry between the dust and light particles into an advantage. In fact, even in the case of strong coupling² of the dust component ($\varGamma _{dd} \gg 1$, as in the case of crystallization), usually the dust-ion interaction is weak, $\varGamma _{di} \le 1$. This means that the ion kinetic energy exceeds the dust-ion interaction energy, and the ion dynamics are only weakly affected by the dust.³ Then, to first order in $\varGamma _{di}$, the ion dynamics can be treated on the mean field level and by neglecting nonlinear effects. This provides the opportunity of using the semi-analytical results for the ions obtained from the solution of the linearized Vlasov equation. Due to their high thermal energy, it can be assumed that the electrons are completely unaffected by the presence of the dust particles, $\varGamma _{de} \ll 1$.

Considering a weak (linear) response of the plasma to the presence of the dust grain, in real space the electrostatic potential of a dust grain screened by ions streaming with the uniform and time-independent velocity $\mathbf{{u}}_i$ becomes [9]

$$\begin{aligned} \varPhi (\mathbf{{r}}) =\frac{1}{(2\pi )^3}\int \! \mathrm {d}^3\mathbf{{k}}\, \frac{\phi _C(k)}{\varepsilon (\mathbf{{k}},\mathbf{{k}}\cdot \mathbf{{u}}_i)} {e}^{{i} \mathbf {k}\cdot \mathbf{{r}}}, \end{aligned}$$

(3.1)

with $\phi _C(k)= Q_d/\varepsilon _0 k^2$ being the Fourier transform of the bare Coulomb potential and $\varepsilon (\mathbf{{k}},\omega )$ being the dynamic dielectric function (Fig. 3.2). In the limit $\mathbf{{u}}_i \rightarrow 0$ the potential (3.1) reduces to the isotropic Yukawa (Debye) potential$\varPhi _Y$.⁴ The dynamically screened potential (3.1) is the main ingredient in the present multiscale approach. The idea to use this potential for the dynamics of dust grains in a complex plasma was first realized by Murillo and co-workers [15, 16] as well as by Joyce and Lampe [11, 17].

They demonstrated that, in fact, wake effects and net attractive dust interactions can be reproduced by this approximation. Despite the success of this model, comparisons with PIC simulations revealed substantial quantitative discrepancies [7]. We have, therefore, developed an independent substantially improved realization of this multi-scale approach that involves a high precision numerical computation of the screened dust potential. The code shows excellent agreement with PIC results (as discussed below).

In the following we briefly summarize the derivation of the dust potential and then discuss how to use it in $N$-particle MD simulations. We start from Maxwell’s equations for a polarizable medium

$$\begin{aligned} \mathrm{div} \mathbf{D}(\mathbf{r},t) = \sum _a q_a n_a(\mathbf{r},t), \end{aligned}$$

(3.2)

where $n_a(\mathbf{r},t)$ is the number density of particles with charge $q_a$. In Fourier space, using the electrodynamic definition of the dielectric tensor ($i,j=x,y,z$), $D_{i}(\mathbf{{k}},\omega )=\sum _j\varepsilon _{ij}(\mathbf{{k}},\omega ) E_{j}(\mathbf{{k}},\omega )$, we obtain for the electrostatic potential,

$$\begin{aligned} \phi (\mathbf{{k}},\omega ) = \frac{q_a n_{a}(\mathbf{{k}},\omega )}{\sum _{ij} k_ik_j \varepsilon _{ij}(\mathbf{{k}},\omega )}. \end{aligned}$$

(3.3)

For the case of unmagnetized electrons and ions streaming with velocity $\mathbf{u}_i$ we take into account the longitudinal plasma response, $\varepsilon _{ij}\rightarrow k_ik_j\varepsilon /k^2$, and obtain the screened potential of a single point-like grain “l” of charge $Q_l$, initially located at position $\mathbf{r}_{0l}$ and moving with velocity $\mathbf{v}_l$ [9]

$$\begin{aligned} \varPhi _l(\mathbf{r}-\mathbf{r}_{0l};t) = Q_l\int \! \frac{\mathrm {d}^3\mathbf{{k}}}{2\pi ^2}\frac{1}{k^2} \frac{e^{i\mathbf{k}(\mathbf{r}_{0l}-\mathbf{v}_l t)}}{\varepsilon \left( \mathbf{k},\mathbf{k}\cdot \left[ \mathbf{v}_l(t)-\mathbf{u}_i\right] \right) }, \end{aligned}$$

(3.4)

recovering expression (3.1). The longitudinal dynamic dielectric function follows from solving kinetic equations for the electrons and ions. Approximating ion collisions by a relaxation time approximation (Bhatnagar-Gross-Krooks collision term, e.g., [18]) with the collision frequency $\nu _i$ and neglecting dynamics effects for the electrons⁵ one obtains

$$\begin{aligned} \varepsilon (\mathbf{{k}},\omega ;\mathbf{R})=1+\frac{1}{k^2\lambda _{De}^2}+\frac{\omega _i^2}{k^2} \frac{\displaystyle \int \! {\mathrm {d}}^3\mathbf{{v}} \, \frac{{\mathbf{{k}}}\cdot \nabla _\mathbf{{v}}f_{i0}(\mathbf{{ v}};\mathbf{R})}{\omega - {\mathbf{{k}}}\cdot \mathbf{{v}}+ i\nu _i}}{1-i\nu _i\displaystyle \int \! {\mathrm {d}}^3\mathbf{{v}} \, \frac{f_{i0}(\mathbf{v};{\mathbf{R}})}{\omega - \mathbf{{k}}\cdot \mathbf{{ v}} + i\nu _i}} \;, \end{aligned}$$

(3.5)

where $\lambda _{De}= \sqrt{ \varepsilon _0 k_B T_e/q_e^2 \bar{n}_e}$denotes the electron Debye length, $f_{i0}(\mathbf{v};\mathbf{R})$ the unperturbed ion velocity distribution function and $\bar{n}_{e(i)}$ and ${T}_{e(i)}$ refer to the mean electron (ion) density and temperature, respectively. The result (3.5) includes Landau damping and collisional damping where $\nu _i$ is typically dominated by ion-neutral collisions. Note that, in the above expressions, one may allow for a space dependence of the ion parameters $\nu _i=\nu _i(\mathbf{R})$.

In most situations of interest the ions will be in (local) thermodynamic equilibrium having a local Maxwellian distribution function $f_{i0}$. Assuming spatially homogeneously distributed electrons, ions and neutrals,⁶ the dielectric function (3.5) is readily computed

$$\begin{aligned} \varepsilon (\mathbf{{k}},\omega )= 1 + \frac{1}{k^2 \lambda _{\mathrm {De}}^2} + \frac{1}{k^2 \lambda _{\mathrm {Di}}^2} \left[ \frac{1+\zeta _i Z(\zeta _i)}{1+\frac{i\nu _{i}}{\sqrt{2} k v_{Ti}}Z(\zeta _i)} \right] , \end{aligned}$$

(3.6)

where we employed the standard substitution

$$\begin{aligned} \zeta _i=[\mathbf{{k}}\cdot \mathbf{{u}}_i+i\nu _{i}]/[\sqrt{2} k v_{Ti}] , \end{aligned}$$

(3.7)

with the thermal velocity

$$\begin{aligned} v_{T\alpha }=(k_B T_\alpha /m_\alpha )^{1/2}, \end{aligned}$$

(3.8)

and introduced the plasma dispersion function [19, 20]

$$\begin{aligned} Z(z)=i \sqrt{\pi } e^{-z^2}\text {erfc}(- i z), \end{aligned}$$

(3.9)

where $\text {erfc}(z)$ is the complementary error function.

Fig. 3.2

Wake potential$\varPhi (\mathbf{{r}})$ around a negatively charged dust grain due to streaming ions. Close to the grain there is a repulsive Yukawa-type potential (blue). Positively charged ions are focused in the streaming direction and create a positive space charge region in the wakefield (black-red) which attracts other grains downstream and gives rise to an non-reciprocal grain interaction

Using expression (3.6), we can compute the dynamically screened dust potentials (3.4) very accurately via a fast Fourier transform on large wave number grids, see Sects. 3.3 and 3.4.1. In a second step of the multiscale scheme, we will use the dust (wake) potentials for $N$-particle LMD simulations.

2.2.2 N-particle Langevin Dynamics Simulations

Our first-principle computational approach to treat strongly correlated dust particles at a finite neutral gas temperature is based on Langevin molecular dynamics simulations. In contrast to the Yukawa one-component plasma model considered in Chap. 1 by Thomsen et al., we now use the dynamically screened dust potentials, (3.4), and we add neutral gas friction (collision frequency $\nu _{dn}$) and a stochastic noise term. The equation of motion for the $k$th dust grain in an external harmonic trap has the form

$$\begin{aligned} m_d \ddot{\mathbf {r}}_k=- \nabla _k V_k^{{\mathrm {eff}}}({\mathbf { r}}_k,t) - \omega _0^2 m_d {\mathbf {r}}_k - \nu _{dn} m_d \dot{\mathbf {r}}_k + {\mathbf {f}}_k(t), \end{aligned}$$

(3.10)

where $f_k$ is a Gaussian white noise, the intensity of which is determined by the neutral gas temperature (fluctuation-dissipation relation, e.g., Ref. [21]). A screening-independent parabolic confinement is explicitly included in (3.10). It mimics the combined effect of gravity, thermophoresis, and electric fields, which in the experiments with Yukawa balls is used to achieve an approximately isotropic harmonic confinement for the dust grains [22].⁷ Depending on the experimental condition, in particular rf-power, this potential is replaced by an anisotropic oscillator potential. The key ingredient in (3.10) is, however, the total dynamic potential acting on the $k$th grain

$$\begin{aligned} V_k^{\mathrm {eff}}(\mathbf{r}_k,t) = Q_d \sum _{l\ne k}^{N} \varPhi (\mathbf{r}_k-\mathbf {r_l,t}), \end{aligned}$$

(3.11)

where, in accord with the present linear response approximation, $V_k^{\mathrm {eff}}$ is the sum of the dynamically screened potentials (3.4) created by all other $(N-1)$ grains. In order to make $N$-particle simulations feasible, an expensive re-computation of the complicated screened potential $\varPhi$ has to be avoided. Instead, this potential is typically pre-computed and stored in a large table.

3 Introduction to the Kielstream Program

Calculation of the linearized potential (3.4) crucially relies on a three dimensional discrete Fourier transform (3D DFT) of a grid of the plasma response function which is defined in $k$-space. Including streaming effects in the model, however, requires the plasma dispersion function (closely related to the Faddeeva function) and makes the calculation non trivial. In 2009 an original code was written [6] using Mathematica [24], as there was no implementation of the Faddeeva function in C/C++ that was reliable across a broad range, see also Ref. [20]. The Mathematica platform has ‘sophisticated built-in automatic numeric precision and accuracy control’, that allows for very high accuracy and virtually arbitrary precision computation. However, due to the complexities of calculating both the plasma polarisation function and a 3D DFT, this code is slow, with runtimes of up to several hours for a medium sized ($256 \times 256 \times 512$) grid. In order to study broader ranges of physical parameters, including high electron-to-ion-temperature systems, higher grid resolutions are necessary, and a faster code is required. Thanks to publication of a new library for calculating the Faddeeva function, libcerf [25], in 2013, which we validated against Mathematica, it is now possible to reliably calculate the plasma response function in C/C++.

Here we therefore introduce Kielstream,⁸ a new linear response program written in C++ to calculate the electric potential around a charged dust particle in a streaming plasma. The code uses the new libcerf library and the C++ FFTW library [26] to calculate the plasma response function and its Fourier transform respectively. Using a combination of symmetry and software optimisations and parallelisation, the code runs for the same grid resolution up to 10000 times faster than the previous Mathematica code. Its results agree well with theory and with the Mathematica code to closer than 1 %.

3.1 Code Structure

The high performance of Kielstream is achieved partly by exploiting the cylindrical symmetry of the problem in different ways:

Fig. 3.3

Radial symmetry of the response function implies there are eight symmetrical triangular sectors, hence we must calculate only one triangular sector, area $N'$, of the $x-y$ cross section, asymptotically reducing calculation time eightfold. Note, the even number of grid elements forces the origin to lie off centre, introducing boundary cases which become less noticeable with increasing $N_r$. This introduces a shift by only one element but has significant repercussions on the Fourier transform, which is very sensitive to symmetry

• Separating the transform Firstly, the 3D DFT assumes linear separability across the three $k$-space dimensions. This allows us to split the transform into two stages, (i) a 2D transformation on each $x-y$ cross section and (ii) 1D transformations in the $z$-direction (Fig. 3.4). Radial symmetry implies only a 2D subspace, one $x-z$ halfplane, is required for the output. This allows us to discard all unnecessary data following the 2D transformation. We retain only data in a spoke along the positive $x$ axis, which greatly reduces the number of 1D transforms required. Furthermore, this splitting means we must only hold one of the $N_z$ 2D cross sections in memory at a time, reducing the size of the problem from $\fancyscript{O} (N_x N_y N_z)$, for the whole grid, to $\fancyscript{O}(N_x N_y + N_x N_z)$, for one cross section and one half plane (Fig. 3.4).

  This optimization greatly enhances the performance and enables both larger grid sizes to be used without extensive memory allocation, and the straightforward introduction of parallelisation on the $N_z$ independent 2D slices, with each array created, populated with the plasma response function and Fourier transformed independently of the others. Even a single call of the OpenMP library [27] improves times (almost) proportionally to the number of processors. Overall, splitting the 3D Fourier transform into two stages and performing the $z$-transforms only along the positive $x$ axis reduces the number of 1D DFTs by $2 N_x$, leaving the $N_z$ 2D DFTs as the main contributors to runtime. Asymptotic complexity of the transform is reduced from $\fancyscript{O} ( N_z N_r ^2 \log (N_z N_r ^2) )$ to $\fancyscript{O} (N_z N_r ^2 \log (N_r ^2) + N_r N_z \log (N_z))$.

• Exploiting cross sectional symmetry Secondly, the grid on which the program operates is cuboidal,⁹ but both the plasma polarisation and its Fourier transform depend only on a $k \cdot v$ scalar product and therefore must be cylindrically symmetric. This means for every $z$ value ($x-y$ cross section), only one triangular section, one eighth of each of the cross sections, is unique (Fig. 3.3). The plasma polarisation function for the seven other symmetrical sections can be found by simply changing the $x$ and $y$ indices (e.g. x$\leftrightarrow$y or x$\leftrightarrow$-x, see pseudocode below). Populating the 3D grid with the plasma polarisation function is typically a very time consuming process but is drastically reduced by taking advantage of the eightfold symmetry. This leaves the 2D Fourier transforms as the rate determining step.

• Removing the static part The singularity at the origin in the screened Coulomb potential can be a problem when performing the numerical transform, for instance causing sampling errors. Following G. Joyce [17], we can exploit the linearity of the Fourier transform to overcome this problem by subtracting the response function for a corresponding static system in $k$-space (a Lorentzian) before the DFT. This Lorentzian has a simple analytic Fourier transform to a Yukawa potential in real space and hence the potential can be added back in afterwards with very high accuracy. This technique also has the advantage of separating the length scales of the Yukawa part and the wake oscillations, leaving a continuous response function purely describing wake effects. If we were Fourier transforming the Lorentzian we would need a larger range in $k$-space to accurately describe the response function, whereas by subtracting it we can focus on the small region around the origin in $k$-space where high resolution is needed.

• Further improvements Another opportunity offered by the symmetry of both the input and the output is calculating the $x$-transformation only upon the positive $y$ halfplane and copying the results into the negative $y$ halfplane (vice versa for the $y$-transformation). This technique was however not employed as the overheads involved outweighed the benefits for grids of $N_x \times N_y \times N_z = 1024 \times 1024 \times 2048$ and smaller.

Fig. 3.4

Method of splitting the 3D DFT first into $N_z$ 2D transforms and then subsequently $N_r = N_x /2$ 1D transforms. The area of the data arrays required and hence transform time and space requirements are dramatically reduced

By default Kielstream performs all operations in dimensionless units scaled by the electron Debye length, with lengths in units of $\lambda _{De}$ and wavevectors in units of its reciprocal. This means both $k$-space and $r$-space ranges are of the order $10-100$. Assuming a net neutral plasma, with equal ion and electron densities ($Z_e=Z_i$), dimensionless units allow the program to be controlled with merely three dimensionless parameters: the Mach number $M$ of the ion flow relative to the plasma sound speed, the ion collision frequency $\nu _i$ in terms of the ion plasma frequency, and the relative electron temperature $T_r = T_e / T_i$. These parameters are all of the order $0.01-100$, maximising floating point accuracy.

Fig. 3.5

Example pseudocode describing the algorithms used by Kielstream. Note the optimization of find_integrand and the separation of the 3D DFT into 2D and 1D components. Using a temporary data array inside the loop of 2D DFTs makes the process thread safe

The code algorithm is organised as shown in Fig. 3.5. The main procedure can be summarised as follows:

• (i) Within a (parallelized) loop calculate the 2D DFTs for each (consecutive) $x-y$ section along the $z$-direction:

  • Create a 2D temporary array, reducing memory requirements compared to the entire 3D grid.

  • Populate 2D array with polarisation function using libcerf, evaluating only for one triangular section of unique values.

  • Calculate 2D DFT using the same FFTW algorithm, saving only data along the positive $x$ axis.

• (ii) After the loop perform all 1/2 $N_x$ 1D DFTs in the $z$-direction.

3.2 Performance and Runtimes

The improvement in speed between Mathematica and Kielstream is stunning. C++ is a faster lower level language without built in accuracy checks, and the use of the techniques mentioned above allow further order of magnitude improvements. The final speed is up to 1000 times faster with no parallelisation on the Intel Core i5 processor. With parallelisation, using the OpenMP routines, this speed is increased by the number of processors. This means the time taken to do the $256 \times 256 \times 512$ grid used as standard in the Mathematica code is reduced from over an hour to under a second with the parallelized C++ code (Table 3.2). A grid of $64$ times the size of Mathematica’s, $1024 \times 1024 \times 2048$, was used, with a runtime of just under a minute. This significantly larger grid size greatly extends the range of physical parameters for which Kielstream gives a high accuracy description of the system. This allows us to overcome the numerical limits formerly required for convergence (e.g. in the collisionless case $T_r \le 25$), which were given in the previous work [6].

Table 3.2 Effect of varying grid sizes on runtimes for Kielstream, using an Intel Core i5 ($4 \times 3.1$ GHz)

Fig. 3.6

Demonstration of aliasing in the imaginary part of the Mathematica results, for $M=1.5, T_r=100, \nu _i=0.1$ at a grid size of $256 \times 256 \times 512$. Physically impossible pseudo-periodicity effects appear upstream of the dust particle, due to undersampling in $k$-space. Kielstream’s capacity for higher resolution allows this effect to be strongly reduced. Note also that the imaginary part has odd radial symmetry, which is caused by a real part in reciprocal-space which has odd symmetry in $k_r$, implying a single element shift in the grid indexing. See Fig. 3.7 for a plot of the corresponding real part of the potential. Take notice of the different colour scale

The larger number of grid points possible with Kielstream allows for a finer resolution that prevents undersampling in $k$-space and, by Nyquist’s theorem, aliasing of downstream features to upstream of the dust particle. Causally, it is impossible for wakefeatures to appear upstream and aliasing is easily spotted giving rise to pseudo periodicity effects as shown in Fig. 3.6.¹⁰

The original Mathematica code allows for a systematic test of Kielstream’s reliability (specifically for smaller grid sizes).¹¹ Replicating the Mathematica grid and physical parameters with Kielstream, the resulting electric potentials generally show good agreement, to better than $1\,\%$, between the real parts of the Mathematica and the Kielstream output (Fig. 3.8). It is, however, clear from Fig. 3.7 that at high Mach numbers and low damping (i.e., low Landau damping$T_i / T_e \rightarrow 0$ and low frictional damping$\nu _i \rightarrow 0$) the codes diverge, despite the agreement of libcerf with Mathematica (up to 16 significant figures) and the same grids and physical parameters.

Fig. 3.7

Comparison between the resulting (real) potential from Kielstream and Mathematica for the same parameters as in Fig. 3.6, using the same (low) grid resolution and ranges. The left panel shows the results from Kielstream and the right the difference compared with Mathematica. Differences are greater than $1\,\%$ for a high relative temperature. At these small grid sizes, both Kielstream and Mathematica have pseudo-periodicity effects on the $0.1$ mV scale

Fig. 3.8

Comparison between the resulting (real) potential from Kielstream and Mathematica for $M=0.5, T_r=10, \nu _i=0.1$, using the same (low) grid resolution and ranges as in Figs. 3.6 and 3.7. The left panel shows the results from Kielstream and the right the difference compared with Mathematica. This shows agreement between Kielstream and Mathematica to better than $1\,\%$ as Landau damping is higher. The difference must derive from intrinsic differences in the programs, which use different data indexing and DFT routines

Fig. 3.9

Imaginary part of the electric potential along $z=0$ (left) and $r=0$ (right) for a grid size of $512 \times 512 \times 1024$, demonstrating a sharp decay along $r$ and constancy along $z$, with sign alternating along both axes. This marks the error caused by a discontinuity at the $z$ boundary of the odd imaginary part of the function in reciprocal space. The amplitude is negligible compared to the real part

The difference in the underlying implementations can also be seen in a non-zero imaginary part of the result for the Mathematica code (Fig. 3.6), which suggests that the Mathematica implementation has an index shift error, as an imaginary electric potential is unphysical. This is due to the DFT routine expecting the origin at the first array index. The resulting imaginary part is also purely odd in $r$, whereas the physical system is cylindrically symmetric in both reciprocal-space and real-space, indicating an error.¹² Kielstream therefore appears more reliable, as its imaginary part is almost everywhere zero, as discussed below (cf. Fig. 3.9).

3.3 Estimation of Numerical Errors

A rough estimate of the errors induced by the finite grid size is given by the imaginary part of the result of the Fourier transform, which should be zero everywhere for a physical electric potential. As opposed to the Mathematica code, the imaginary part in Kielstream does not follow the real wake profile (as in Fig. 3.6) but is instead sharply peaked around the $z$ axis (up to three or four elements from the origin) and is of constant amplitude in $z$ (Fig. 3.9). The oscillating sign with a period of two points along both $r$ and $z$ indicates by the Fourier shift theorem that the error is an artifact arising from a feature at the boundary, while the constant amplitude in $z$ implies that it originates from a discontinuity in $k$-space. This is due to the inherent numerical limits of a finite integration interval, where the function must be cut off before it reaches zero. When the function is made periodic, this results in a discontinuity in the imaginary part when going from positive to negative $k_z$ values. This effect can be reduced by increasing the physical range in the $k_z$-direction over which the plasma polarisation function is evaluated, or else by increasing the axial resolution, as shown in Table 3.3.

Table 3.3 Effect of varying axial resolution $N_z$ and axial range on the amplitude of errors originating from edge effects

For a $512 \times 512 \times 1024$ grid with a $k_z$ range of 50 $\lambda _{De}^{-1}$ (to be precise, [$-25:25$]), the maximum imaginary part is of order $10^{-6}$ mV, and hence compared to data of order $10$ mV is negligible. Furthermore, it can be effectively reduced to below $10^{-8}$ mV by using a sufficiently large $k_z$ range. Note, as the real part of the function has even symmetry, it has no such discontinuity in reciprocal space and the imaginary part is merely an indication of the amplitude of the error in real space, and not of its precise form.

4 Simulation Results

Wake effects are well known from objects moving in water (birds, ships). Behind the object a periodic modulation of the water surface is observed, connected with a characteristic opening angle. In Cartesian coordinates, the height of the surface gravity wake is approximately given by

$$\begin{aligned} h(r,z)=\int _{-\pi /2}^{\pi /2} \! \cos [(\tilde{z}-\tilde{r} \tan (\vartheta ))/\cos (\vartheta ) ] \, \mathrm {d}\vartheta , \end{aligned}$$

(3.12)

with $\tilde{z} = g\cdot z/u_z^2$ and $\tilde{r} = g\cdot r/u_z^2$, where $u_z$ denotes the ship’s speed and $g=9.81\,\text {m/s}^2$ the gravitational acceleration [28]. This pattern (Kelvin’s wave pattern) is shown in the bottom part of Fig. 3.10. In the following, we will see that dust particles in a streaming plasma show a very similar behavior.

4.1 Wake Structure Around a Single Grain

Fig. 3.10

Top: longitudinal 3D plasma wake $\phi (r,z)$ computed with Kielstream on a $4096\times 16384$ element sized grid for $M=0.7, T_r=100$, and $\nu _{i}=0.0$. The point-sized dust grain is located at the origin. The stationary flow of ions along the z-direction leads to strong deviations from the Yukawa potential by giving rise to an anisotropic, oscillating wake structure behind the grain. The solid blue, black, and orange curves are equipotential lines at $\phi =\{-1,0,1\}$ mV, respectively. The angle of the V-shaped wake depends on the Mach number $M$, cf. Fig. 3.11 Bottom: Kelvin’s wave pattern of a ship located at the origin and moving with constant speed $|u_z|=5$ m/s on deep water (in the reference frame where the ship is at rest). Equipotential lines are shown for the wave heights $h=\{-10,0,10\}$ cm, respectively. The V-shaped pattern has a characteristic angle $\varphi =\arcsin (1/3)\approx {19.5}{^\circ }$ (dashed gray lines) which is generally considered to be independent of the ship’s speed [29]

The presence of the dust grain perturbs the plasma around it. Using Kielstream, we now can evaluate the impact of the directed ion flow on the response of the plasma, (3.4), with very high numerical accuracy, even resolving the long tail of the wakefield in a collisionless plasma, see Fig. 3.10. At finite ion flow velocities, $M>0$, the streaming ions are deflected by attraction to the grain giving rise to an oscillatory wakefield with regions of an enhanced (respectively reduced) ion density. Therefore, the dynamically screened potential around the grain is highly anisotropic and depends on the spatial orientation relative to the plasma flow. In particular, the strong trailing peak in the ion wake pattern can be sufficient to overcome the mutual repulsion of charged grains giving rise to a net attractive grain-grain interaction and the formation of particle strings.

Fig. 3.11

The effect of the Mach number$M$ for two different relative temperatures $T_r=30$ (upper half figures) and $T_r=100$ (lower half figures) at finite damping $\nu _i=0.1$. The Mach number increases from top left to bottom right, showing change from an isotropic Yukawa potential at $M=0$ to formation of increasingly curved wavefronts $\phi =0$ (dark solid lines), tending towards the distinctive Mach angle. Contours at $-1$, $0$ and $1$ mV demonstrate the wavefronts and the shape of the wake pattern. It is clear that the higher temperature ratio supports a stronger response, especially in producing a more elongated wake pattern. Note that even in the absence of collisions with neutrals, the amplitude of the wake oscillations damps out due to Landau damping which naturally limits the range of the wakefield

Figure 3.11 gives an overview of the effect of increasing Mach number on the electric grain potential for representative plasma parameters. The relative temperature $T_r$ is $30$ in the upper half of the figures and $100$ in the lower half. It is immediately clear that the isotropic Yukawa potential fails dramatically at finite flow velocities. Even in the subsonic regime, $M<1$, streaming distorts the potential away from an isotropic Yukawa shape and towards a conical wavepacket. The severity of the distortion depends on the electron/ion temperature ratio $T_r$, and is stronger at the higher temperature ratio (corresponding to weak Landau damping), which supports a much longer wavepacket. Equally spaced peaks reach higher amplitude, as increasing ion flow, with greater ion kinetic energy, leads to a more pronounced wake structure with several maxima and minima. As the stream becomes supersonic, the wavefront $\phi = 0$ shows the information barrier along cones defined by the Mach angle, which in contrast to Kelvin’s wave pattern, Fig. 3.10, does depend on $M$.

It is interesting to note that in the static case, $M=0$, the negative potential of the dust grain is predominantly screened by a positively charged ion cloud, which isotropically forms around the grain. The Debye screening length of the ions, $\lambda _{Di}=(\varepsilon _0 k_B T_i/\bar{n}_i q^2_i)^{1/2}$, is significantly shorter (and contribute more to screening) than the electron Debye length $\lambda _{De}=(\varepsilon _0 k_B T_e/\bar{n}_e q^2_e)^{1/2}$. Note, particularly in the top left panel of Fig. 3.11, that the total Debye length $\lambda _{D} ^{-2} = \lambda _{De} ^{-2} + \lambda _{Di} ^{-2} = \lambda _{De} ^{-2} (1+T_r)$, and thus the range of the Yukawa potential, varies for the different relative temperatures. With increasing $M$, the trajectories of fast moving ions are less affected by the grain and the plasma ions contribute less to the screening. The effective Debye length $\lambda _D=\lambda _D(M)$ decreases. In the supersonic limit, $M \rightarrow \infty$, the spherical symmetry of the Debye screening is restored and entirely determined by the electrons [6].¹³

Fig. 3.12

Plot of electric potential (red) and resulting axial force acting upon a second particle (blue) against position for a nearly collisionless system, with $M=1.0, T_r=100$ and $\nu _i=0.01$. Potential along the $z$-axis (red) changes from the electron only screened Yukawa potential in the upstream direction to the ion dominated wake oscillations downstream. Near the dust particle at the origin the deep potential minimum resembles the isotropic electron and ion screened Yukawa potential of the corresponding static case ($M=0$, dashed black). The electric force in the $z$-direction (blue) attracts a second dust particle to equally spaced points in the wake of the first (around $z=1.2, 7.7$ and $14.2 \lambda _{De}$). At this low damping the potential off-axis (gray, spaced every $0.3 \lambda _{De}$ in radius) does not decay rapidly and instead is shifted downstream compared to the on-axis oscillations

Figure 3.12 demonstrates the electric potential for a typical charge¹⁴ of $-10\,000 e_0$ and the resulting axial force upon a second identical particle for weak damping ($M=1.0$ with low Landau damping$T_r=100$ and friction$\nu _i=0.01$). The force is simply the $z$-gradient of the potential multiplied by a negative charge of $10^4 e_0$ and is calculated in a subroutine of Kielstream. Note the smoothness in the calculated force function, which is crucial for accurate MD simulations. The wake oscillations are strongly pronounced, both on-axis and off-axis (spaced every $0.3 \lambda _{De}$ radially), with the force attracting the second dust particle to regularly spaced points in the wake (the zeros of the force function).

4.1.1 Comparison of Linear Response and PIC Results

At this point, it is instructive to compare these results obtained in the framework of linearized-response kinetic-theory for a point charge with fully nonlinear PIC simulations of the stationary plasma flow past a finite-sized grain charge, see Figs. 3.13 and 3.14. We find that the linearized potential agrees very well with collisionless (non-linear) DiP3D-PIC simulations by W. Miloch [5, 6]. Both complementary approaches yield the same number of potential extrema where the positions of the maxima and minima, the peak heights as well as the topological structure of the wakefield including the characteristic angle of the wave front are correctly reproduced. This qualitative and quantitative agreement is even more impressive when one takes into account that, for computational reasons, the PIC simulations used a grain charge of several times larger than the experimental values, which naturally increases nonlinear effects.

Fig. 3.13

Contour plots of the screened grain potential obtained from full 3D PIC (left) and the corresponding linear response result (right) for a collisionless plasma with $T_r=10$. The grain is marked by the black dot and has a radius $a=0.185\lambda _{De}$ (PIC only). The supersonic ion flow ($M=1.5$) is from left to right. Attractive potential values are shown in yellow and red. The agreement is excellent, see also Fig. 3.14. The PIC simulations are due to Miloch [6]. Reprinted with permission from [35]

Fig. 3.14

Peak positions of the wake potential as function of Mach number M. Red (blue) lines correspond to a positive (negative) space charge. The dashed lines show the linear behaviour over broad ranges. Diamonds: 3D PIC results of Miloch. From Ref. [6]. Reprinted with permission from [6]

Extensive systematic comparisons show that linear response is able to yield reliable results for the effective potential of dust grains in non-equilibrium complex plasmas with streaming ions. Due to its high numerical accuracy, the present dynamical screening approach is well suited for a detailed theoretical analysis of correlated dust systems and for quantitative comparisons with experiments. Moreover, the comparison of both simulation methods is also a valuable test for PIC, since the dynamical screening approach does not suffer the noise and convergence problems of PIC codes for realistic grain charges. On the other hand, PIC helps to estimate an upper bound for the importance of nonlinear effects setting a natural limit of applicability of our present linear response approach. In particular for low Mach-numbers $M<0.5$, deviations are expected to increase, since then the ions are more strongly affected by the dust.

4.2 Many-Particle Langevin Dynamics Simulations

Having obtained high-quality linear response results for the dynamically screened dust potential we are now in the position to investigate many-body properties of these systems as discussed in the beginning, Sect. 3.2.2. In particular, we can evaluate the structural and thermodynamic properties, phase transitions and even time-dependent properties in a system of many strongly correlated dust particles in the presence of streaming ions, plasma wakes and attractive forces.

Using the multiscale concept based on (3.10) we have performed Langevin molecular dynamic simulations for $N=46$ dust grains and plasma parameters that match the typical experimental conditions: grain charge $Q_d=-6000\,e_0$ (radius $R_d=2.43\,\upmu \text {m}$), electron temperature$T_e=2.5$ eV, ion temperature $T_i=0.03$ eV, and argon gas pressure$p=15$ Pa which corresponds to an ion collision frequency (in units of the ion plasma frequency) of $\nu _{i}/\omega _{pi}=0.2$. A dust-neutral collision frequency of $\nu _{dn}=19.1$ Hz drives the dust temperature toward the neutral gas temperature $T_n = T_i$. Assuming singly charged argon ions, the electron density equals the ion density $\bar{n}_e=\bar{n}_i=10^8\,\text {cm}^{-3}$, and we obtain for the total Debye screening length $\lambda _{Di}=128.0\,\upmu \text {m}$, which is mainly due to the ions ($\lambda _{Di}=128.8\,\upmu \text {m}$, $\lambda _{De}= 1175\,\upmu \text {m}$). The external confinement is isotropic and harmonic with the trap frequency being $\omega _0=7.0$ [30]. We want to point out that all input parameters are closely related to the experimental parameters. There are no free “fitting” parameters in the simulations resulting in a predictive power that is comparable to that of PIC simulations.

Fig. 3.15

Simulation snapshots of $N=46$ dust grains in a spherically confined complex plasma in presence of ions streaming from top to bottom. Depending on the ion Mach number $M$ completely different self-organized dust structures are observed: a Yukawa ball with a (1,12,33) shell configuration (cluster size $a=2.2$ mm),b ion flow destabilises the plasma crystal; the grains are spatially delocalized ($a=3.0$ mm), c formation of ’dust molecules’; vertically aligned pairs move through a weakly coupled amorphous state ($a=6.3$ mm), d wake attraction leads to formation of flow-aligned particle chains ($a=7.0$ mm). The color code for $M=0.01, 0.08$ denotes the particle’s radial distance from the trap center. Reprinted with permission from  [30]

Varying the Mach number $M$, our multi-scale simulation approach reproduces the experimentally observed cluster configurations in the two limiting cases of the ion flow velocity see Fig. 3.15a and d:

• 1. Without streaming, $M=0$, we reproduce strongly correlated Yukawa balls [1, 23] consisting of several nested spherical shells. The number of shells and even the exact shell population numbers observed in the experiments are perfectly reproduced by the Yukawa interaction [31].

• 2. At a supersonic streaming velocity, $M=1$, a completely different type of dust structure is observed: under the influence of an attractive wakefield, the grains align behind each other forming particle strings.

In the latter case, the streaming ions couple kinetic energy into the non-Hamiltonian dust system¹⁵ which leads to self-excited vibrations which cause a destabilization of longer strings. As observed in the experiments, lower grains are directly following the motion of the upper ones due to the non-reciprocal wakefield attraction. The amplitude of the particle oscillations grows in the streaming direction. This can be seen in Fig. 3.15d where the upper part of the particle strings are highly ordered while in the lower part grain dislocations appear due to the downward increasing, ion streaming-induced dust temperature [14, 16, 30].

Moreover, our simulations reveal a discontinuous transition between these two limits where the grains are found to from regular structures. In fact, a relatively moderate ion flow, $M \approx 0.1$, destabilizes the highly ordered Yukawa balls and initiates an abrupt order-disorder transition. For the considered plasma conditions, the critical value of $M$ for this abrupt, non-equilibrium melting process is found to be independent of cluster size. Increasing $M$ more and more grains line up behind each other forming flow-aligned particle complexes and finally, at larger $M$ values, elongated chains as shown in Fig. 3.15.

In both mentioned limiting cases (i) and (ii), the grains are strongly coupled, while in an intermediate range of Mach numbers they are in a weakly coupled amorphous state. The reason for this surprising finding is that in the static case, $M=0$, the strong mutual grain repulsion is compensated by an external confining potential. Just this stabilizing interplay allows for the strong interparticle correlations and even crystallization. At low $M$ values, however, the grain potential in downstream direction becomes non-monotonic and relatively flat. Consequently, the repelling force between the grains vanishes and the stabilizing force balance breaks down giving rise to an amorphous many-particle state. Only with further increase of the ion flow, a new order mechanism of local nature takes charge. This mechanism, however, does not stabilize the system as a whole, but rather, individual grains agglomerate to larger complexes due to the wakefield attraction. That is, a global stabilization mechanism is replaced by a local one.

Interestingly, we find that already a relatively moderate ion flow is sufficient for wake attraction and the onset of string formation. This behavior was also observed in recent experiments [32]. Current PIC simulations suggest, however, that wakefield effects disappear for $M$ less than approximately $0.3$ [8]. This discrepancy for low Mach numbers shows that details of the associated processes are still poorly understood and also underlines the demand for conclusive experimental studies.

5 Synopsis

Only a few years ago, it was a widely accepted that plasma wakefields and an effective particle attraction exist only if the speed of the ion flow exceeds the ion-acoustic velocity, e.g., Ref. [12], and until today there are only very few theoretical calculations for the subsonic regime. However, this regime is of broad interest for many current experiments where grains are confined in the pre-sheath region or the plasma bulk [33–35].

In order to correctly describe the non-equilibrium nature of a realistic plasma, including ion flows, we presented a multi-scale dynamical screening approach for partially ionized complex plasmas. This linear-response/molecular dynamics hybrid approach provides the unique opportunity to study the impact of plasma wakes in stationary flowing plasmas on the dynamical, correlated interplay of many dust grains with unrivalled precision [14, 16, 30].

The scheme is based on a linearized kinetic-theory treatment of the ion flow past the grain charge. The quality of the plasma wakefield depends fully on the precise numerical evaluation of rather complex integrals on large three-dimensional grids which even today is not routine. In order to improve the computational efficiency and to allow for higher grid resolutions, Kielstream, a parallelized high-performance linear response code has been developed utilizing the FFTW library [26] for the discrete Fourier transform and a very recent implementation of the plasma dispersion function by Zaghloul et al. (algorithm 916, [20, 25]).

Our multi-scale simulations reveal a remarkable structural transition from spherical Yukawa balls ($M=0$) to flow-aligned strings when the ion Mach number $M$ is increased. Recent experiments on confined systems [35] allow to systematically analyse the competition of spherical order which is induced by the external confinement, on the one hand, and ion-focus induced attraction of like-charged particles and chain formation under subsonic flow conditions, on the other hand. Since subsonic flows occur in a broad range of situations this is one of the central questions that has importance far beyond the dusty plasma community, in particular for warm dense matter [2, 3].