Keywords

12.1 Introduction

In the structural health monitoring research community, damage identification is defined as the process of determining: (1) existence of damage; (2) location of damage; (3) severity of damage; and (4) remaining useful life of structures [1]. Among many methods that have been proposed in the past two decades [2–4], finite element (FE) model updating methods are popular for damage identification [5–9] because they directly provide information about the existence, location, and extent of damage, and because in some cases the updated FE model can also be used for damage prognosis. These methods have been successfully applied for damage identification of civil structures in recent years [10–14]. In the FE model updating methods, a set of structural model parameters, usually stiffness of finite elements, is adjusted so that the model predicted quantities of interest, modal parameters in this study, best match those obtained from the test data. Damage identification through FE model updating is usually performed in two steps: a baseline/reference model is calibrated in the first step to match the data at the undamaged state of the structure, and in the second step, another model is fitted to the data of the damaged structure. The difference between the two models indicates the location and extent of damage.

The baseline model parameters are expected to be close to their corresponding values assigned in the initial FE model, as the initial model and its parameters are created based on the best level of engineer’s knowledge and based on the experimental test data. This expectation is not fulfilled when large modeling errors exist. In this case, the model parameters of the initial model usually need large and in many cases unrealistic modifications to fit to the undamaged state data. These unrealistic modifications often try to compensate for different sources of modeling errors. Moreover, our previous studies [14, 15] indicated that the estimated damage and updated model parameters are highly sensitive to the variability and uncertainty of identified modal parameters used in model updating and to the relative weights between the modal parameters.

This paper proposes a damage identification process through a single set of FE model updating, i.e., there is no need for a reference/baseline model. To this end, a new likelihood function is defined based on data from both the damaged and undamaged states of the structure. The initial FE model is directly used for damage identification in one step.

Performance of the proposed method is studied when applied to numerically simulated responses of a nine-story building. Effects of different factors such as modeling errors, measurement noise, data incompleteness in terms of number of modes and number of mode shape components (number of sensors), and different weight factors are on the accuracy of damage identification results are studied. Moreover, the obtained results are compared to those from two other types of likelihood functions used by other researchers. The considered test bed structure is the nine-story SAC building [16]. The original model is modified to reflect the effects of modeling errors. To evaluate the performance of the proposed likelihood for different severity of structural damage, three levels of damage are considered.

12.2 SAC Nine-Story Building

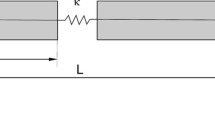
The original SAC nine-story steel moment frame, designed for Los Angeles, California, is shown in Fig. 12.1. The floor masses are reported as 73.10 kips s2/ft for the roof, 67.86 kips s2/ft for floors 9 to 3, and 69.04 for floor 2. For simplicity, the floor masses are all considered as lumped masses and only in horizontal direction in this study. Steel elastic Young’s modulus is considered as 29,000 ksi.

Fig. 12.1
figure 1

Original SAC nine-story steel moment frame [16]

Full size image

To simulate the effects of fabrication and construction errors, the following changes are assumed for the real building. The true/exact structural model is shown in Fig. 12.2 as model M0 and includes the following changes to the original SAC model:

Fig. 12.2
figure 2figure 2

Models M0–M3 (modeling errors circled)

Full size image
  1. (a)

    Second floor is moved 1″ downward.

  2. (b)

    Fourth floor is moved 2″ upward.

  3. (c)

    Sixth floor is moved 2″ downward.

  4. (d)

    Ninth floor is moved 2″ upward.

  5. (e)

    Axe B is moved 2″ to the right, while axes A and C are fixed.

  6. (f)

    Axe E is moved 1″ to the left, while axes D and F are fixed.

  7. (g)

    Elastic Young’s modulus of W14x500 and W36x160 is set as 29,011 ksi.

  8. (h)

    Elastic Young’s modulus of W14x455 and W36x135 is set as 29,021 ksi.

  9. (i)

    Elastic Young’s modulus of W14x283 and W30x99 is set as 29,008 ksi.

  10. (j)

    Elastic Young’s modulus of W14x257, W14x233, W24x68, and W27x84 is set as 29,015 ksi.

  11. (k)

    First floor’s support is horizontally bounded with a spring of stiffness 2.9 × 105 kips/in.

  12. (l)

    The supports on the basement are modeled with rotational springs with the stiffness of 1.16 × 107 kips-in/rad.

  13. (m)

    Mass of the roof is set as 73.25 kips s2/ft; floor 9 to 6 as 67.20 kips s2/ft; floor 6 to 3 as 68.30 kips s2/ft; and floor 2 as 68.54 kips s2/ft. Mass of first floor is also set as 68.54 kips s2/ft.

In order to evaluate the accuracy of damage identifications in the existence of modeling errors, the model updating process will be performed for the true model (labeled as M0) as well as the following three structural models each with different level of modeling errors:

  • M1. Minor modeling errors: all the changes to the original SAC model (points a to m) are considered. The modeling error is in the column sections. Sections between the second floor and third floor are modeled as the section used in the first story (in the true model, upper half and lower half have different sections). Sections between fourth and fifth floors are assigned as the sections used between third to fourth floor; sections between sixth and seventh floors are assigned as sections used between fifth to sixth floor; and finally sections between eighth and ninth floors are assigned as sections used between seventh to eighth floors.

  • M2. Moderate modeling errors: contains modeling errors of M1 and also neglects points g to j and point l. The basement supports are all modeled as pins.

  • M3. Large modeling errors: contains all the errors of M1 plus those induced by neglecting points a to m. The bay lengths and story heights are modeled as shown in Fig. 12.1. The story masses in this model are assumed as: 73.10 for the roof, 67.86 for floors 9 to 3, and 69.04 for floor 2. The first floor’s support is modeled as a pin in the horizontal direction.

The four considered structural models M0–M3 are shown in Fig. 12.2. Modeling errors in the plot of each model are circled. Note that these FE models are not considered as different model classes during the Bayesian FE model updating. The modal assurance criterion (MAC) values between mode shapes of model M1–M3 and those of the true model (M0) are reported in Table 12.1. Since model M3 has nine DOFs with non-zero masses, a maximum of nine modes are considered for damage identification. Modes 8 and 9 of the true model cannot both be formed in the model M3. For the eighth mode of model M3, MAC values are calculated with both eighth and ninth mode of model M0. As it can be seen from Table 12.1, higher modes are more affected by modeling errors. The MAC values of the first five modes are all close to one, but they reduce for higher modes (0.59 for eighth mode of model M2). Natural frequencies of the four models are also reported in Table 12.2.

Table 12.1 MAC values between mode shapes of models M1 to M3 to those of model M0
Full size table
Table 12.2 Natural frequencies of models M0–M3 in undamaged state
Full size table

12.3 Bayesian FE Model Updating

This section presents a summary of the Bayesian FE model updating formulation used in this study. More detailed formulation of the Bayesian model updating process can be found in seminal publications on this topic [17–20]. According to the Bayes theorem, conditional posterior probability distributions of updating parameters θ and σ given the measured data D (identified modal parameters in this study) and the model class M can be obtained by multiplying the likelihood function p(D|θ, σ λ , σ Φ), the conditional prior probability distribution of model parameters p(θ, σ λ , σ Φ|M), and a constant c.

$$ p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda },{\sigma}_{\Phi}\Big|\mathbf{D},M\right)= cp\left(\mathbf{D}\Big|\boldsymbol{\uptheta}, {\sigma}_{\lambda },{\sigma}_{\Phi},M\right)p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda },{\sigma}_{\Phi}\Big|M\right) $$
(12.1)

The likelihood function is the probability of the measured data given the updating model parameters, and the normalization constant c is to ensure that the posterior probability density function (PDF) integrates to one. Three likelihood functions are considered in this study, the first two have been used by many researchers in the past, labeled as likelihoods A and B, and the third likelihood, labeled as likelihood C, is proposed in this paper.

12.3.1 Likelihood A

This likelihood function is based on the assumption of independent zero-mean Gaussian error functions, each defined as the difference between the model-calculated and identified modal parameters [17].

$$ {e}_{\lambda_m}=\frac{{\tilde{\lambda}}_m-{\lambda}_m\left(\boldsymbol{\uptheta} \right)}{{\tilde{\lambda}}_m}\propto N\left(0,{\sigma}_{\lambda_m}\right) $$
(12.2)
$$ {\mathbf{e}}_{\Phi_m}=\frac{{\tilde{\boldsymbol{\Phi}}}_m}{\left\Vert {\tilde{\boldsymbol{\Phi}}}_m\right\Vert }-{a}_m\frac{\boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m\left(\theta \right)}{\left\Vert \boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m\left(\theta \right)\right\Vert}\propto N\left(\mathbf{0},{\sigma}_{\Phi_m}\mathbf{I}\right) $$
(12.3)
$$ p\left(\mathbf{D}\Big|\boldsymbol{\uptheta}, {\sigma}_{\lambda_{1:m}},{\sigma}_{\Phi_{1:m}}\right)=\frac{1}{{\left(\sqrt{2\pi}\right)}^{N_m}{\displaystyle \prod_{m=1}^{N_m}{\sigma}_{\lambda_m}}}{e}^{-\frac{1}{2}{\displaystyle \sum_{m=1}^{N_m}\frac{{\left({e}_{\lambda_m}\right)}^2}{\sigma_{{}_{\lambda_m}}^2}}}\times \frac{1}{{\left(\sqrt{2\pi}\right)}^{N_m{N}_s}{\displaystyle \prod_{m=1}^{N_m{N}_s}{\sigma}_{{\boldsymbol{\Phi}}_m}}}{e}^{-\frac{1}{2}{\displaystyle \sum_{m=1}^{N_m}\frac{e_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}{\sigma_{{}_{{\boldsymbol{\Phi}}_m}}^2}}} $$
(12.4)

where \( {\tilde{\lambda}}_m,{\tilde{\boldsymbol{\Phi}}}_m \) are identified eigen-frequency and mode shape of mode m, and λ m , Φ m are the model-calculated modal parameters. N m is number of identified modes, N s is number of mode shape components, and a m is the mode shape scaling factor. For simplicity, the number of updating model parameters are reduced by assuming a fixed ratio between the standard deviations of eigen-frequency and mode shape errors, \( {N}_s{\sigma}_{\Phi_m}^2={\sigma}_{\lambda_m}^2 \), and also assuming identical standard deviations of the eigen-frequency errors for all the modes. The posterior PDF can then be written as:

$$ p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda}\Big|\mathbf{D},M\right)=\frac{c^{\prime }}{{\left(\sqrt{2\pi}\right)}^{N_m\left({N}_s+1\right)}{N}_s^{\frac{N_m{N}_s}{2}}{\sigma}_{\lambda}^{N_m\left({N}_s+1\right)}}{e}^{-\frac{1}{2{\sigma}_{{}_{\lambda}}^2}{\displaystyle \sum_{m=1}^{N_m}{\left({e}_{\lambda_m}\right)}^2+\frac{1}{N_s}{e}_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}}p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda}\Big|M\right) $$
(12.5)

If the prior PDF is taken as a uniform distribution, the posterior can be further simplified to:

$$ p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda}\Big|\mathbf{D},M\right)=\frac{c}{{\left(\sqrt{2\pi}\right)}^{N_m\left({N}_s+1\right)}{N}_s^{\frac{N_m{N}_s}{2}}{\sigma}_{\lambda}^{N_m\left({N}_s+1\right)}}{e}^{-\frac{1}{2{\sigma}_{{}_{\lambda}}^2}{\displaystyle \sum_{m=1}^{N_m}{\left({e}_{\lambda_m}\right)}^2+\frac{1}{N_s}{e}_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}} $$
(12.6)

The most probable structural model parameters can be obtained as:

$$ \widehat{\boldsymbol{\uptheta}}={\displaystyle \underset{\boldsymbol{\uptheta}}{ \arg }} \min {\displaystyle \sum_{m=1}^{N_m}{\left({e}_{\lambda_m}\right)}^2+\frac{1}{N_s}{e}_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}} $$
(12.7)

In order to estimate structural damage using this likelihood function, the most probable (maximum a-posteriori or MAP) structural model parameters need to be calculated once using the data of the undamaged structure (baseline model parameters) and once using the data of the damaged structure. The difference of the two is regarded as the most probable structural damage.

12.3.2 Likelihood B

This likelihood is based on the assumption of zero-mean Gaussian error functions, each defined as the residuals of eigen-equation using FE model’s stiffness and mass matrixes and identified modal parameters [20]:

$$ {\mathbf{e}}_m=\mathbf{K}\left(\boldsymbol{\uptheta} \right){\tilde{\boldsymbol{\Phi}}}_m-{\tilde{\lambda}}_m\mathbf{M}{\tilde{\boldsymbol{\Phi}}}_m\propto N\left(\mathbf{0},{\boldsymbol{\Sigma}}_m\right) $$
(12.8)

The posterior probability of the model parameters can be written as Eq. 12.9 if the prior is taken as a uniform distribution:

$$ p\left(\boldsymbol{\uptheta}, \boldsymbol{\Sigma} \Big|\mathbf{D}\right)=\frac{c}{\sqrt{{\left(2\pi \right)}^{N_m}{\displaystyle \prod_{m=1}^{N_m} \det \left({\boldsymbol{\Sigma}}_m\right)}}}{e}^{-\frac{1}{2}{\displaystyle \sum_{i=1}^{N_m}{\left({e}_m\right)}^T{\boldsymbol{\Sigma}}_m^{-1}\left({e}_m\right)}} $$
(12.9)

By assuming identical prediction error standard deviations for different modes, the most probable (MAP) estimates of structural model parameters can be obtained as:

$$ \widehat{\boldsymbol{\uptheta}}={\displaystyle \underset{\boldsymbol{\uptheta}}{ \arg }} \min {\displaystyle \sum_{m=1}^{N_m}{\left({e}_m\right)}^2} $$
(12.10)

Same as likelihood A, two sets of model updating are needed to estimate structural damage.

12.3.3 Likelihood C

This proposed likelihood function contains the information of modal parameters both in the damaged and undamaged states of the structure. Therefore, there is no need for updating a reference model using the undamaged data; the initial model can be used for damage identification. The error functions are defined based on the differences between changes from the undamaged to the damaged modal parameters computed from the model and those obtained from measured data. In this likelihood, it is assumed that the ratio of model-predicted eigen-frequencies in the damaged and undamaged states is close to the ratio of identified eigen-frequencies in the damaged and undamaged states. Also the difference of the model-predicted mode shapes in the damage and undamaged states is assumed to be similar to the difference of identified mode shapes in the damaged and undamaged states. The prediction errors are defined as:

$$ {e}_{\lambda_m}=\frac{\lambda_m^d\left(\boldsymbol{\uptheta} \right)}{{\tilde{\lambda}}_m^d}-\frac{\lambda_m^h}{{\tilde{\lambda}}_m^h}\propto N\left(0,{\sigma}_{\lambda_m}\right) $$
(12.11)
$$ {\mathbf{e}}_{\Phi_m}=\left(\frac{{\tilde{\boldsymbol{\Phi}}}_m^d}{\left\Vert {\tilde{\boldsymbol{\Phi}}}_m^d\right\Vert }-{b}_m\frac{{\tilde{\boldsymbol{\Phi}}}_m^h}{\left\Vert {\tilde{\boldsymbol{\Phi}}}_m^h\right\Vert}\right)-\left({a}_m^d\frac{\boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m^d\left(\boldsymbol{\uptheta} \right)}{\left\Vert \boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m^d\left(\boldsymbol{\uptheta} \right)\right\Vert }-{a}_m^h\frac{\boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m^h}{\left\Vert \boldsymbol{\Gamma} {\boldsymbol{\Phi}}_m^h\right\Vert}\right)\propto N\left(\mathbf{0},{\sigma}_{\Phi_m}\mathbf{I}\right) $$
(12.12)

where b m is either 1 or −1 to assure the two mode shapes are in the same direction. The superscript d denotes the modal parameters in the damaged state and the superscript h denotes the undamaged/healthy state modal parameters. The likelihood will be obtained as:

$$ p\left(\mathbf{D}\Big|\boldsymbol{\uptheta}, {\sigma}_{\lambda_{1:m}},{\sigma}_{{\boldsymbol{\Phi}}_{1:m}}\right)=\frac{1}{{\left(\sqrt{2\pi}\right)}^{N_m}{\displaystyle \prod_{m=1}^{N_m}{\sigma}_{\lambda_m}}}{e}^{-\frac{1}{2}{\displaystyle \sum_{m=1}^{N_m}\frac{{\left({e}_{\lambda_m}\right)}^2}{\sigma_{{}_{\lambda_m}}^2}}}\times \frac{1}{{\left(\sqrt{2\pi}\right)}^{N_m{N}_s}{\displaystyle \prod_{m=1}^{N_m{N}_s}{\sigma}_{{\boldsymbol{\Phi}}_m}}}{e}^{-\frac{1}{2}{\displaystyle \sum_{m=1}^{N_m}\frac{e_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}{\sigma_{{}_{{\boldsymbol{\Phi}}_m}}^2}}} $$
(12.13)

\( {\tilde{\lambda}}^h \) is the mean value of identified eigen-frequencies for a certain mode in the undamaged condition and \( {\tilde{\boldsymbol{\Phi}}}^h \) is the mean identified mode shape in the undamaged condition. The estimated model parameters obtained from this likelihood are very close to their initial values if the structure is not damaged. Thus the main sources of error for the damage estimates will be due to the measurement noise or other sources of variations in the measured data, but not due to the modeling errors (when the above-mentioned assumptions are valid). In this case, although modeling errors still exist, their effects do not significantly affect the model updating results.

Considering the same assumptions on the standard deviation terms as in likelihood A, Eq. 12.13 can further be simplified as:

$$ p\left(\mathbf{D}\Big|\boldsymbol{\uptheta}, {\sigma}_{\lambda}\right)=\frac{1}{{\left(\sqrt{2\pi}\right)}^{N_m\left({N}_s+1\right)}{\sigma}_{\lambda}^{N_m\left({N}_s+1\right)}{\sqrt{N_s}}^{N_m{N}_s}}{e}^{-\frac{1}{2{\sigma}_{\lambda}^2}{\displaystyle \sum_{m=1}^{N_m}{\left({e}_{\lambda_m}\right)}^2+\frac{1}{N_s}{e}_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}} $$
(12.14)

The most probable structural damage can be identified as in Eq. 12.7.

FE model updating is performed for the three likelihood functions using the first six eigen-frequencies and full mode shapes of the structure at undamaged state. Note that no noise is added to the data. The estimated MAP values are listed in Table 12.3. As it can be seen, the model M0 does not need any modification in its stiffness regardless of the likelihood type as it has no modeling errors. However, likelihoods A and B imply modifications in the structural stiffness of model M1–M3. These changes in structural stiffness are estimated to compensate the modeling errors and are not due to damage. Larger modeling errors require larger changes in structural stiffness: change in story stiffness is up to 11 % for model M1, 18 % for model M2, and 26 % for model M3. These large modifications for undamaged condition cannot be easily justified and accepted by practicing engineers who use these FE models for design and reliability analysis of structures. These modifications can be much larger for real-world, full-scale structures with larger modeling errors. However, this problem can be avoided by using the proposed likelihood function, as no modification is required in the initial model. This will help the understanding of engineers as the models are created based on the best level of engineer’s knowledge and the model parameter values are set as the expected values derived from experiences or experimental/laboratory tests.

Table 12.3 Model parameters in undamaged state (using six modes)
Full size table

12.4 Damage Identification

Overall ten model parameters are updated: one standard deviation (σ λ ), and nine structural model parameters (θ) each defined as the effective Young’s modulus of all the beams and columns of a story. Four damage scenarios are considered:

  • D0 (no damage)

  • D1 (small damage): θ2 = 0.9, i.e., 10 % loss of stiffness in the beams and columns of the second story.

  • D2 (moderate damage): [θ2 θ3 θ7] = [0.7 0.8 0.8]

  • D3 (severe damage): [θ1 θ2 θ3 θ4 θ7] = [0.7 0.5 0.6 0.8 0.7]

The effective elastic Young’s moduli of the finite elements in damaged structure are defined as E i  = θ i E 0 , where θ i is the model parameter of i th story, E 0 is the undamaged effective Young’s modulus and E i is the damaged effective Young’s modulus of i th story. Natural frequencies of the exact model (M0) in all four damage states are listed in Table 12.4. These natural frequencies and their corresponding mode shapes will be considered as the “identified” modal parameters in the absence of noise and are used for FE model updating. The identified modal parameters of the structure in the undamaged state are those obtained similarly from model M0 in the undamaged state D0.

Table 12.4 Natural frequencies of model M0 for damage scenarios
Full size table

Performance of the three likelihood functions (A-C) for structural damage identification is studied in Sect. 12.4.1 in the presence of modeling errors but absence of measurement noise. Effects of number of identified modes are studied by using 3, 6, and 9 modes during FE model updating process. Effects of measurement noise are studied in Sect. 12.4.2. Section 12.4.3 investigates the effects of using incomplete mode shapes (i.e., number of sensors) for likelihood functions A and C. Finally, effects of weight factor between the eigen-frequency errors and mode shape errors are studied in Sect. 12.4.4 for likelihood C.

12.4.1 Effects of Modeling Errors and Number of Modes

The effects of number of modes used in the model updating process are studied in the absence of measurements noise and assuming the identified mode shapes are complete. The most probable damage values are calculated by Eq. 12.7 for likelihoods A and C and Eq. 12.10 for likelihood B.

The estimated MAP values for the stiffness parameters of damage scenario D2 are listed in Tables 12.5, 12.6 and 12.7 for different number of modes used during FE model updating. The results for damage scenarios D1 and D3 are not listed, but will be explained in the following. If the absolute difference of the identified damage and the true damage is more than 0.05E 0 (i.e., 5 %), the identified damage is shown by bold font and is considered as poor identification. The un-conservative damage (underestimated damage) identification cases are underlined in the tables to provide a better sense of the reliability of the results.

Table 12.5 Model updating results for damage scenario D2 (using all modes except 8)
Full size table
Table 12.6 Model updating results for damage scenario D2 (using the first six modes)
Full size table
Table 12.7 Model updating results for damage scenario D2 (using the first three modes)
Full size table

For the exact model M0, damage is always predicted accurately with no bias since there are no modeling errors. One interesting observation is that the number of poor identifications (bold values), regardless of the likelihood type, is 11 when nine modes are used, 2 when six modes are used, and 4 when only three modes are used. The same trend is observed for damage case D3 as well, and overall, number of poor identification cases for all the damage states and all the models and likelihood types are 38, 19, and 14 for the cases of using 9, 6, and 3 modes, respectively. Number of un-conservative damage identifications are 20, 7, and 7 for the cases of using 9, 6, and 3 modes in the updating. Therefore, the extra information of modes 7–10 did not improve the accuracy of damage identifications in the presence of modeling errors. This might be due to the fact that modeling errors have larger effects on the higher modes as discussed in Sect. 12.2. Based on this observation, it is recommended to avoid using the experimental mode shapes that cannot be perfectly paired (i.e., has low MAC) with one of the initial FE model mode shapes during FE model updating.

The identification results from the damage case D3 have larger errors than the results from less severe damage cases D1 and D2, i.e., the error in damage estimates increases by increasing damage levels for all the three likelihoods. In damage case D1 all the three likelihoods predict the damage with reasonable accuracy. Number of poor identification cases is 30, 11, and 30 and number of un-conservative identifications is 14, 7, and 10 for likelihoods A, B, and C respectively considering all the models and damage states. Likelihood B is much more successful because it can consider the dependency of the natural frequencies and mode shapes. However, it should be mentioned that in a real application when few DOFs are measured, the errors of likelihood B will increase because of the errors in the prediction of missing mode shape components. This likelihood is not easily applicable in practice as mode shapes are usually incomplete. Model reduction techniques and mode shape expansion techniques are not accurate enough and therefore the added errors will undermine benefits of using this likelihood function in practice. In addition, 17 and 16 cases of poor identifications of likelihoods A and C belong to the case of using nine modes, therefore, by excluding the modes that are highly affected by the modeling errors, these two likelihoods become reliable as well.

12.4.2 Effects of Noisy Measurements

To study the effects of measurement noise and modal identification errors, the “identified” modal parameters are polluted by Gaussian white noise. Noise vectors with coefficients-of-variations (COVs) of 0.5 and 2 % are added to the exact modal parameters to simulate the noisy “identified” modal parameters. Twenty realizations of the noisy modal data sets are simulated for each damage case (D0–D3) and FE model updating is performed for each of the data sets separately. The estimated damage is defined as the average of difference between model parameters in the damaged and undamaged states. The results are very similar to the results of previous section and therefore are not presented here. It is concluded that all the three likelihoods are capable of predicting the damage with reasonable accuracies in the presence of measurement noise. Nevertheless, the updating model parameters have large variations in the case of using only three modes, indicating that the amount of information provided by the first three modes may not be enough for estimation of the nine structural model parameters.

Figure 12.3 shows the histograms of the most probable structural model parameters θ 1 to θ 4 in the undamaged state and the damage state of damage scenario D2 for the three likelihoods. The first column corresponds to likelihood A, the second column to likelihood B and the third column shows the results from likelihood C. All the results are obtained using model M2 and consider the first six modes for model updating process. The first and fourth model parameters are not damaged; therefore their updated model parameters are distributed almost in the same area for both damaged and undamaged states for all the three likelihood. However, these regions are not the same. For example, the θ 1 are distributed from 1.0 to 1.3 for likelihood A, 0.7–0.9 for likelihood B, and 0.9–1.1 for likelihood C. This substructure is not damaged and its expected updated value is around 1.0 for both the damaged and undamaged states. This expectation is only satisfied for likelihood C. Same is true for the other three model parameters, as their updated model parameters are distributed around 1.0 in the undamaged state and in the damage state if the substructure is not damaged.

Fig. 12.3
figure 3

Histograms of updating model parameters using model M2 and the first six modes. Undamaged state (gray bars) and damaged state D2 (dark bars)

Full size image

12.4.3 Effects of Number of Sensors

In this section, the effects of having incomplete mode shapes are studied on the performance of FE model updating for damage identification using likelihood functions A and C. Two cases of sensor configurations are considered, the first configuration considers seven sensors at stories 2, 3, 4, 5, 7, 8, and 10, and the second considers five sensors at stories 2, 4, 6, 8, and 10. Overall, damage identification results based on both likelihood functions are acceptable. Tables 12.8, 12.9 and 12.10 report the model updating results when using five sensors and the first six modes for the three damage scenarios D1–D3, respectively. In the case of having seven sensors (three mode shape components missing), overall 10 and 14 cases of poor identifications are observed for likelihoods A and C. Number of un-conservative damage identifications is 4 and 6. In the case of having five sensors, number of poor identification is 13 and 23, and number of un-conservative damage identifications is 5 and 11 for likelihoods A and C respectively. Obviously, using more sensors improve the accuracy of the results. Note that likelihood A provides more accurate results than likelihood C, however, likelihood C has the advantages described in previous sections. Also, the performance of this likelihood can be improved by using proper modes during identification process and using the optimal weight factor.

Table 12.8 Model updating results for damage scenario D1, using six modes and five sensors
Full size table
Table 12.9 Model updating results for damage scenario D2, using six modes and five sensors
Full size table
Table 12.10 Model updating results for damage scenario D3, using six modes and five sensors
Full size table

12.4.4 Effects of Weight Factors

The results of previous sections are all based on specific assumptions (fixed ratios) between the standards deviations of the error terms. Assigning higher standard deviation for an error term (specific modal parameter) corresponds to giving lower weight to that modal parameter. The model updating results are sensitive to the assumed relationship between error variations. This section investigates the effects of different assumptions on the weight factors between eigen-frequency errors and mode shape errors. The study is performed only for likelihood C with the first six modes identified and using five sensors. Similar studies is performed for evaluating the effect of weight factor on likelihood A in [21, 22].

It is still assumed that the COVs of errors for all the modes are all identical. A weight factor is defined for the relation between the COVs of eigen-frequency errors and mode shape errors:

$$ {\sigma}_{\Phi}^2=w{N}_s{\sigma}_{\lambda}^2 $$
(12.15)

Accordingly, the likelihood function can be written as:

$$ p\left(\boldsymbol{\uptheta}, {\sigma}_{\lambda}\Big|\mathbf{D},M\right)=\frac{c}{{\left(\sqrt{2\pi}\right)}^{N_m\left({N}_s+1\right)}{N}_s^{\frac{N_m{N}_s}{2}}{\sigma}_{\lambda}^{N_m\left({N}_s+1\right)}}{e}^{-\frac{1}{2{\sigma}_{{}_{\lambda}}^2}{\displaystyle \sum_{m=1}^{N_m}{\left({e}_{\lambda_m}\right)}^2+\frac{1}{N_s}{e}_{{\boldsymbol{\Phi}}_m}^T{e}_{{\boldsymbol{\Phi}}_m}}} $$
(12.16)

Table 12.11 presents the updating parameters at damage state D3, using model M2, the first six identified modes, and five sensors. These results can be viewed as pareto optimal solutions. The weight factor, w, was set as 1 in previous sections. The maximum change for an updating parameter is 0.14, however, some parameters show less sensitivity to the variations of the weight factor. It can be seen that the accuracy of identification results in this specific application can be improved by using lower weight factors, which increases the relative importance of mode shape residuals.

Table 12.11 Identified damage for damage case of D3, for different weight factors
Full size table

12.5 Conclusions

A new likelihood function is proposed to be used in the FE model updating of civil structures. This likelihood function is expected to provide more accurate model updating results for damage identification in the presence of modeling errors. The identified modal data at both undamaged and damaged state of the structure are used in this likelihood function and therefore, damage identification can be performed through just one FE model updating, i.e., the new likelihood function does not require estimation of reference/baseline model at the undamaged state. This has an important practical advantage because the initial FE model is usually created based on the best level of engineer’s knowledge, and is based on experimental tests and measurements. Large modifications of the initial model may not be physically meaningful. It is shown that the proposed likelihood provides the similarly accurate damage identification results as the other types of likelihoods that are commonly used in the literature.

Three different levels of modeling errors and three damage scenarios are considered to evaluate the performance of the three considered likelihood functions for damage identification. It is observed that all the three likelihoods can successfully identify damage in the absence of modeling error or when modeling errors are small. Moreover, it is observed that regardless of the level of modeling errors and the likelihood function used, the identification results are accurate for small amounts of damage (D1). However, the identification errors increase by increasing the severity of damage and modeling errors. In this application modeling errors affect the higher modes much more significantly than the lower modes. Therefore, the FE model updating results can be improved by avoiding using the identified modes with low MAC values with the FE model counterparts. This study also reveals that assigning optimal relative weights between the eigen-frequency and mode shape error functions can slightly improve the damage identification results. The proper choice of vibration modes and the optimum weight factor in the likelihood function can be determined using Bayesian model class selection or Bayesian model averaging.