Keywords

46.1 Introduction

With increasing progress of design and analysis techniques and the advent of new materials, are being designed and built structures increasingly slender and flexible. But limited available land in big cities is causing these structures to be constructed nearby each other. These structures are thus more vulnerable to excessive vibrations caused by dynamic loads, such as earthquakes, winds and human occupation [1]. These vibrations are undesirable in a structural perspective.

Structural control is an alternative, widely used in recent decades, for protection of civil structures This technology has been used for seismic mitigation and nowadays is a well-established research area in structural dynamics and engineering practice [2, 3]. Structural control devices can be classified as passive, active, semi-active, and hybrid systems.

Hybrid control is a combination of passive and active control. It has been widely studied since it is a control alternative which supplies the main disadvantages of passive and active control isolated. Passive control main disadvantage is to lose performance when the dynamic excitation is out of the frequency range that it was designed. Active control, although not having this deficiency requires large amounts of energy to generate control forces. Hybrid control systems, besides needing low control forces magnitudes and being efficient in a large frequency range is a more robust and reliable control [1].

It is noticeable that due to the few available land still available in large urban centers, structures such as high buildings have been constructed very close to each other. Based on this fact, in last years the so called structural coupling method has been proposed, it is an efficient structural control technique [4]. It consists of connecting two neighboring buildings through a coupling device, with the aim of reducing the undesirable dynamic effects, taking advantage of the mechanical properties of each structure. In this way it is possible to control both structural responses simultaneously, that is specifically attractive for this technique. The idea of connecting two different structures through control devices have been explored since the early 1970 by Klein [5, 6].

Theoretical approaches, numerical and experimental of structures using coupled passive control strategies, active, semi-active and hybrid have been performed since the 1990 [6–9]. The feasibility of these strategies has been demonstrated in several analytical studies [9–16], as well as in experimental investigations [9, 13, 14, 16].

All above mentioned studies showed that good performance of control methods using coupling depends on the adjacent building properties, like natural frequencies and number of floors, besides the connector mechanical properties. Due to the potential of the structural coupling technique, this papers aims to study the behavior of two structures connected by two passive linear dampers, working together with a set of active control systems installed in each structure. It is proposed a passive control system of a damper set that work as the connecting elements between buildings. Besides passive dampers, one or more active devices are combined to the coupled system. As a result, different settings of hybrid (passive + active) control are obtained, that can be proper to different levels of seismic protection. All the results here obtained are compared with the non-coupled case. The control system devices considered in this work are linear devices [17].

46.2 Two-Building Mathematical Models

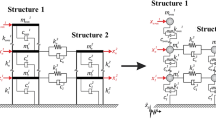
Consider building 1 and building 2, showed in Fig. 46.1, having n + m stories and n stories, respectively. The mass, shear stiffness, and damping coefficients for the ith story are m 1 i , k 1 i and c 1 i for building 1 and m 2 i , k 2 i and c 2 i for building 2. The damping and stiffness coefficient of the damper at the ith floor are \( {\widehat{c}}_i^1 \) and \( {\widehat{k}}_i^1 \), respectively. The equation of motion for the structure of Fig. 46.1 is given by:

$$ \boldsymbol{M}\ddot{\boldsymbol{x}}(t)+\boldsymbol{C}\dot{\boldsymbol{x}}(t)+\boldsymbol{Kx}(t)=\boldsymbol{T}_U\boldsymbol{u}(t)+{\boldsymbol{T}}_w\ddot{\boldsymbol{x}}(t) $$
(46.1)

where M (n + m × n + m), C (n + m × n + m) and K (n + m × n + m) are the mass, stiffness, and damping matrices of the coupled structure, respectively, including the stiffness and damping coefficients of the buildings 1 and 2, well as the stiffness and damping coefficients of the connecting devices; x(t) the vector (n + m × 1) of story displacements with respect to the ground; u(t) (n + m × 1) is the vector of control forces; T u (n + m × n + m) is the control forces location matrix; T w (n + m × n + m) is the external forces location matrix and \( \ddot{\boldsymbol{x}}(t) \) is the ground acceleration.

Fig. 46.1
figure 1

Structural model of adjacent buildings with connecting dampers

Full size image

Mass, stiffness and damping matrices, M, K and C, of the coupled structure are defined as follows:

$$ \begin{array}{lll}[b]{\boldsymbol{M}}_{2n+m,2n+m}&=\left[\begin{array}{c@{\quad}c}{M}_{n+m,n+m}^1 & 0 \\ 0 & {M}_{n,n}^2 \end{array}\right]\\ {\boldsymbol{K}}_{2n+m,2n+m}&=\left[\begin{array}{c@{\quad}c} {K}_{n+m,n+m}^1 & 0 \\ 0 & {K}_{n,n}^2 \end{array}\right]+\left[\begin{array}{c@{\quad}c} {\widehat{K}}_{n+m,n+m}^1 & {0}_{n+m,n} \\ {0}_{n,n+m} & {\widehat{K}}_{n,n}^1 \end{array}\right]\\ {\boldsymbol{C}}_{2n+m,2n+m}&=\left[\begin{array}{c@{\quad}c} {C}_{n+m,n+m}^1 & 0 \\ 0 & {C}_{n,n}^2 \end{array}\right]+\left[\begin{array}{c@{\quad}c} {\widehat{C}}_{n+m,n+m}^1 & {0}_{n+m,n} \\ {0}_{n,n+m} & {\widehat{C}}_{n,n}^1 \end{array}\right]\\ {\widehat{K}}_{n+m,n+m}^1&=\left[\begin{array}{c@{\quad}c@{\quad}c} {k}_1^1 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {k}_{nD}^1 \end{array}\right],{\widehat{C}}_{n+m,n+m}^1=\left[\begin{array}{c@{\quad}c@{\quad}c} {c}_1^1 & 0 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & {c}_{nD}^1 \end{array}\right]\end{array} $$
(46.2)

The matrices \( {\widehat{K}}^1 \) and \( {\widehat{C}}^1 \) corresponds to the linking systems; c 1 nD and k 1 nD denotes the damping and stiffness coefficients of the ith building in the nth story. Usually, the formulation and solution of control problems present system equations of motion (46.1) as state equations:

$$ \dot{\boldsymbol{z}}(t)=\boldsymbol{Az}(t)+\boldsymbol{Bu}(t)+\boldsymbol{E}\ddot{\boldsymbol{x}}(t) $$
(46.3)

were z(t) is the state vector 4n + 2m; A corresponds to the matrix system state 4n + 2m × 4n + 2m; B and E are the control and disturbance input matrices; Finally, the vector \( \dot{\boldsymbol{z}}(t) \) represents the state of the structural system which contains the relative velocity and responses to acceleration of the structure with respect to the ground. The details of each vector and matrix are listed as follows:

$$ \boldsymbol{z}(t)=\left[\begin{array}{c} \boldsymbol{x}(t) \\ \dot{\boldsymbol{x}}(t) \end{array}\right],\boldsymbol{A}=\left[\begin{array}{c@{\quad}c}0 & I \\ -{\boldsymbol{M}}^{-1}\boldsymbol{K} & -{\boldsymbol{M}}^{-1}\boldsymbol{C} \end{array}\right],\boldsymbol{B}=\left[\begin{array}{c} 0 \\ {\boldsymbol{M}}^{-1}{\boldsymbol{T}\!}_U \end{array}\right],\boldsymbol{E}=\left[\begin{array}{c} 0 \\ -{1}_{n+m,1} \end{array}\right]$$
(46.4)

To perform the numerical simulation of the seismic response corresponding to the different passive and active control configurations presented in the next sections, the f building parameters shown in Table 46.1 have been used [3]:

Table 46.1 Parameters of the structures used in numerical modeling
Full size table

The damping matrices are calculated using the Wilson and Penzien method [18], employing a damping coefficient ξ = 3 %. Finally, a record of the North–South ground acceleration corresponding to El Centro 1940 earthquake has been used as seismic excitation to simulate the vibrational response of the buildings.

46.3 Classical Linear Optimal Control

In the development of active control system, one of the key steps is to set an appropriate control law, which is obtained via the control algorithm. In the present study the algorithm of classical linear optimal control is used.

The linear optimal control problem consist in finding the control vector u(t) that minimizes the performance index J subject to the constraint (46.3). In structural control, the performance index is usually chosen as a quadratic function in z(t) and u(t), as follows

$$ J={\displaystyle \underset{t_0}{\overset{t_f}{\int }}\left[{\mathbf{z}}^{\mathbf{T}}(t)\mathbf{Qz}(t)+{\mathbf{u}}^{\mathbf{T}}(t)\mathbf{Ru}(t)\right] dt} $$
(46.5)

where Q is a 2n × 2n positive semi-definite matrix and R is a m × m positive definite matrix. The matrices Q and R are referred to as weighting matrices, whose magnitudes are assigned according to the relative importance attached to the state variables and to the control forces in the minimization procedure. The minimization problem leads to a Riccati differential equation system of the form

$$ \begin{array}{l}\overset{.}{\mathbf{P}}(t)+\mathbf{P}(t)\mathbf{A}-\dfrac{1}{2}\mathbf{P}(t)\mathbf{B}{\mathbf{R}}^{-\mathbf{1}}{\mathbf{B}}^{\mathbf{T}}\mathbf{P}(t)+{\mathbf{A}}^{\mathbf{T}}\mathbf{P}(t)+2\mathbf{Q}=\mathbf{0},\\ {}\mathbf{P}\left({t}_f\right)=\mathbf{0}\end{array} $$
(46.6)

where P(t) is the Riccati matrix. The control vector u(t) is linear in z(t). In this case, the linear optimal control law is

$$ \mathbf{u}(t)=\mathbf{G}(t)\mathbf{z}(t)=-\frac{1}{2}{\mathbf{R}}^{-\mathbf{1}}{\mathbf{B}}^{\mathbf{T}}\mathbf{P}(t)\mathbf{z}(t) $$
(46.7)

where \( \mathbf{G}(t)=-\frac{1}{2}{\mathbf{R}}^{-\mathbf{1}}{\mathbf{B}}^{\mathbf{T}}\mathbf{P}(t) \) is the control gain.

46.4 Coupling Configuration via Passive Dampers

In this section, buildings are connected via a passive device, and the coupled system is subjected to a seismic excitation. In this case, the T u matrix which defines the control force locations has all elements equal to zero. Thus, the state-space model (46.3) takes now the form

$$ \dot{\boldsymbol{z}}(t)=\boldsymbol{Az}(t)+\boldsymbol{E}\ddot{\boldsymbol{x}}(t) $$
(46.8)

The connecting element is a passive linear viscous damper. This damper dissipates energy by converting mechanical energy into heat, reducing stress and displacements in the structure, since the viscous damper varies the damping force according to velocity [19]. The dampers available nowadays have damping coefficient (c d ) in the range 1–50 kNs/mm [20].

A parametric study was performed aiming to find the best damping coefficient c d , varying the number and position of the connection devices. Figure 46.2 presents schematically eight different coupling configurations analyzed. Case (a) corresponds to the uncoupled system; cases (b)–(h) are semi-coupled configurations, in other words, semi-coupled indicate that not all of the floors are connected; the case (e) is considered a full-coupled system.

Fig. 46.2
figure 2

Passive coupling configurations

Full size image

For each case it was calculated maximum relative displacement using different values of c d . The range of c d values considered was 0–30 kNs/mm where c d  = 0 indicates that the buildings were not coupled, while for high values of c d , the connection between the structures would simulate a rigid connection. Figure 46.3a, b show the results obtained for each case of coupling configuration.

Fig. 46.3
figure 3

Maximum relatives displacements. (a) Building 1, (b) Building 2

Full size image

Observing Fig. 46.3a corresponding to building 1, it can be noticed that relative displacements decrease as the c d value increases, reaching excellent results for cases (e), (g) and (h). Only case (d) presented a worse performance, since the relative displacements decreased did not decreased substantially in comparison with the uncoupled case. On the other hand, best results for Structure 2 were those with c d values less than 5 kNs/mm. From this value, the relative displacements increase reaching higher values than those obtained for the structure without coupling (c d  = 0). Case (d) presented an unfavorable behavior, since it is required a high c d value compared with other models to reduce the maximum relative displacement.

Therefore, it can be concluded that the most indicated choice for better performance would be c d equal to 3.5 kNs/mm, since this value, for most cases, presented a considerable decrease in the maximum relative displacement in both buildings. Moreover, considering the better number and position of dampers configuration case (h) would be indicated, installing viscous dampers located in second and third floors.

46.5 Hybrid Control Coupling Configurations

Next it was studied the combined operation of passive damping inter-building control systems and local active control systems installed in the buildings, resulting in a hybrid control system. Suppose that the actively controlled buildings are equipped with ideal active bracing devices installed between every two consecutive stories as shown in Fig. 46.4. Developing an active control system need the appropriate control law choice, which is obtained through the control algorithm adopted. In this work it was considered the classical optimal linear control algorithm [21].

Fig. 46.4
figure 4

Active bracing system

Full size image

Three different configurations for installing active bracing were studied varying their number and position, as it can be seen in Fig. 46.5. The best result obtained on the last section for passive coupling, was to install viscofluid dampers on the second and third floors [case (h)]. This configuration was also considered here to the hybrid system, as it can be also observed in Fig. 46.5.

Fig. 46.5
figure 5

Hybrid control coupling configurations

Full size image

The maximum relative displacements obtained for these analyses are presented in Fig. 46.6a, b for the buildings 1 and 2, respectively. In this figure, it can be observed that in all cases the response decreases in comparison with the uncontrolled structures. It emphasizes that in building 1, cases (a) and (c) presented approximately the same results, with a reduction of about 53 %. In case (b) the reduction was only about 12 %, significantly lower than the other two cases. In Structure 2, in all three cases there was a reduction, case (c) lead to better performance with a reduction of 48 %, and case (a) presented the lower reduction of 27 %.

Fig. 46.6
figure 6

Maximum absolute relative displacements for hybrid control coupled system

Full size image

Analyzing the two cases, it can be concluded that the most efficient configuration would be case (c), but taking in account system cost and maintenance, case (a) would be the most suitable, since considerably reduces the maximum response of building 1 and provides a satisfactory reduction for building 2.

Table 46.2 presents maximum control forces obtained for each case. There was little change in force control maximum values for both structures, varying configurations, and the values found are within the capacity range of actuators available in the market nowadays.

Table 46.2 Control maximum forces obtained for the hybrid system models
Full size table

46.6 Conclusions

The behavior of two near buildings connected by passive dampers, setting up a coupled structure, was studied. A combination of active and passive control elements was studied to design a variety of control schemes to mitigate the seismic response of a two-building system. A parametric study varying the viscous damper coefficient was performed, also the number and positioning of the devices was analyzed. It was observed that high values of damping coefficient can amplify one of the structure response. It was not necessary to install connecting devices in all floors to achieve the better performance.

Also a combination of active and passive control elements was carried out to design a variety of control schemes to mitigate the seismic response of a two-building system. Based on the results obtained, it can be concluded that in the case of hybrid coupling, configuration (a) would be the most suitable for the structural system analyzed. Furthermore, it can be said that the active bracing was more important in reducing Building 1 response and for building 2 most of the response reduction was caused by passive interconnection elements. The passive linking system had no adverse effect on the performance of the local active control systems; moreover, it guarantees a remarkable level of seismic protection in case of failure of any of the local active control systems.