Keywords

3.1 Introduction

Because nonlinearities have an influence on the vibrations of most mechanical structures, it is relevant to study their effects on the evolution of the oscillations with respect to a certain parameter, e.g., the frequency of an external excitation or a system parameter. Continuation algorithms prove to be appropriate tools to carry out such analyzes [1]. Besides, the study of the bifurcations of periodic solutions is also of interest because of the key role played by these bifurcations in structural dynamics. During the continuation of periodic solutions, one can encounter several kinds of bifurcation, namely the limit point (LP), Naimark-Sacker (NS), branch point (BP) and period doubling (PD) bifurcations. While LPs are encountered in the neighborhood of resonance peaks, the presence of NSs indicates the existence of quasiperiodic oscillations in the vicinity of the bifurcation. In that regard, detecting these bifurcations and eventually tracking them in the parameter space gives a more complete understanding of the nonlinear systems.

In the literature, there are several possibilities to approximate a steady-state periodic solution x(t) in order to compute a branch of solutions of the same family. Among others, one can cite methods in the time domain such as the orthogonal collocation and the shooting techniques, and methods in the frequency domain such as the harmonic balance (HB) method. In the time domain, the computation of a periodic solution is achieved through the resolution of a boundary value problem (BVP). The shooting technique [2] consists in optimizing the initial state of the system, which is the unknown of the shooting problem, so that the signal obtained from a time integration of the equations of motion with this initial state is periodic. Although the performance of this technique is interesting in the case of low-dimensional structures, its application to large-scale structures is usually more computationally demanding. Indeed, the numerous time integrations drastically slow down the speed of the algorithm. Moreover, an efficient bifurcation tracking procedure coupled with the shooting technique still has to be investigated. In this sense, the orthogonal collocation could seem as a good alternative. This method, which proposes a discretization of the BVP, is widely utilized in software for bifurcation detection and tracking like auto [3], colsys [4], content [5], matcont [6] or, more recently, coco [7]. It has the advantage of solving problems, including those with difficulties like singularities, with a high accuracy. However, it is rarely used to study large systems, which can for example be explained by the considerable memory space this method requires for the discretization of the problem.

Among all methods in the frequency domain, the HB method, also known as the Fourier–Galerkin method, is certainly the most widely used. Through an approximation of the periodic signals with their Fourier coefficients, which are the new unknowns of the problem, the user can have a direct control on the accuracy of the solutions. First implemented for analyzing linear systems, the HB method was then successfully adapted to nonlinear problems, in electrical (e.g., [8]) and mechanical engineering (e.g., [9, 10]) for example. The main advantage of the HB method is that it involves algebraic equations with less unknowns than the methods in the time domain, for problems for which low orders of approximation are sufficient to obtain an accurate solution, which is the case if the regime of the system is not strongly nonlinear. For this reason, the HB method has received increased attention for the last couple of years, which has led to numerous applications and adaptations of the method (e.g., [11, 12]) and to the development of a continuation package manlab [13, 14]. Nevertheless, in spite of its performance and accuracy, to the authors’ knowledge the HB method has never been extended to track bifurcations. Furthermore, it is rarely exploited for its filtering property in the study of the dynamics of nonlinear systems, for which the spectrum of the responses can be much richer than the spectrum of the excitation. The purpose of this work is to address this extension of the HB method.

The theoretical part of this work is devoted to the presentation of the harmonic balance method and to its implementation for bifurcation tracking. Then the method will be validated using a large-scale model of a spacecraft, which will highlight the filtering feature of the method on the study of normal modes and will show the accuracy of the method in the presence of strong nonlinearities. As a second application, the study of a nonlinear vibration absorber will illustrate the bifurcation tracking as a mechanical design tool.

3.2 Harmonic Balance Method

This section performs a brief review of the theory of the HB method. The method will be applied to general non-autonomous nonlinear dynamical systems with n degrees of freedom (DOFs) whose equations of motion are

$$\displaystyle{ \mathbf{M}\ddot{\mathbf{x}} + \mathbf{C}\dot{\mathbf{x}} + \mathbf{K}\mathbf{x} = \mathbf{f}_{l}(\omega,t) -\mathbf{f}_{nl}(\mathbf{x},\dot{\mathbf{x}}) = \mathbf{f}(\mathbf{x},\dot{\mathbf{x}},\omega,t) }$$
(3.1)

where M, C and K are the mass, damping and stiffness matrices respectively, x represents the displacements, the dots refer to the derivatives with respect to time t, f nl represents the nonlinear forces and f l stands for the periodic external forces (harmonic excitation, for example) with frequency ω. The term f gathers both the linear and nonlinear forces.

As recalled in the introduction, the periodic solutions x(t) and f(t) of eom) are approximated by Fourier series truncated to the N H -th harmonic:

$$\displaystyle{ \begin{array}{l} \mathbf{x}(t) = \mathbf{c}_{0}^{x} +\sum\nolimits_{ k=1}^{N_{H}}\left (\mathbf{s}_{k}^{x}\sin \left (\frac{k\omega t} {\nu } \right ) + \mathbf{c}_{k}^{x}\cos \left (\frac{k\omega t} {\nu } \right )\right )\\ \\ \mathbf{f}(t) = \mathbf{c}_{0}^{f} +\sum\nolimits_{ k=1}^{N_{H}}\left (\mathbf{s}_{k}^{f}\sin \left (\frac{k\omega t} {\nu } \right ) + \mathbf{c}_{k}^{f}\cos \left (\frac{k\omega t} {\nu } \right )\right ) \end{array} }$$
(3.2)

where s k and c k represent the vectors of the Fourier coefficients related to the sine and cosine terms, respectively. Here it is interesting to note that the Fourier coefficients of f t, c k f and s k f, depend on the Fourier coefficients of the displacements x t, c k x and s k x. The integer parameter ν is introduced to account for some possible subharmonics of the external excitation frequency ω.

Substituting expressions (3.2) in Eq. (3.1) and balancing the harmonic terms with a Galerkin projection yields the following nonlinear equations in the frequency domain

$$\displaystyle{ \mathbf{h}(\mathbf{z},\omega ) \equiv \mathbf{A}(\omega )\mathbf{z} -\mathbf{b}(\mathbf{z},\omega ) = \mathbf{0} }$$
(3.3)

where A is the \(\left (2N_{H} + 1\right )n \times \left (2N_{H} + 1\right )n\) matrix describing the linear dynamics of the system, z is the vector containing all the Fourier coefficients of the displacements x(t), and b represents the vector of the Fourier coefficients of the (external) linear and nonlinear forces f(t). They have the following expressions:

$$\displaystyle\begin{array}{rcl} \mathbf{A}& =& \left [\begin{array}{cccc} \mathbf{K}& && \\ &\begin{array}{cc} \mathbf{K} -{\left (\frac{\omega }{\nu }\right )}^{2}\mathbf{M}& -\frac{\omega }{\nu }\mathbf{C} \\ \frac{\omega }{\nu }\mathbf{C} &\mathbf{K} -{\left (\frac{\omega }{\nu }\right )}^{2}\mathbf{M} \end{array} && \\ & &\ddots& \\ & &&\begin{array}{cc} \mathbf{K} -{\left (N_{H}\frac{\omega } {\nu }\right )}^{2}\mathbf{M}& - N_{ H}\frac{\omega } {\nu }\mathbf{C} \\ N_{H}\frac{\omega } {\nu }\mathbf{C} &\mathbf{K} -{\left (N_{H}\frac{\omega } {\nu }\right )}^{2}\mathbf{M} \end{array}\\ \end{array} \right ], \\ \mathbf{z}& =& \left [\begin{array}{c} \mathbf{c}_{0}^{x}\\ \\ \mathbf{s}_{1}^{x}\\ \\ \mathbf{c}_{1}^{x}\\ \vdots\\ \\ \mathbf{s}_{N_{H}}^{x}\\ \\ \mathbf{c}_{N_{H}}^{x} \end{array} \right ],\mathbf{b} = \left [\begin{array}{c} \mathbf{c}_{0}^{f}\\ \\ \mathbf{s}_{1}^{f}\\ \\ \mathbf{c}_{1}^{f}\\ \vdots\\ \\ \mathbf{s}_{N_{H}}^{f}\\ \\ \mathbf{c}_{N_{H}}^{f} \end{array} \right ]{}\end{array}$$
(3.4)

In the time domain, expression (3.1) contains n equations while, in the frequency domain, expression (3.3) have 2N H + 1n unknowns gathered in z. Expression (3.3) can be seen as the equations of amplitude of (3.1): if z ∗ is a root of (3.3), then the time signals x ∗ constructed from z ∗ with (3.2) are solutions of the equations of motion (3.1) and are periodic.

3.2.1 Analytical Expression of the Nonlinear Terms and of the Jacobian Matrix of the System

Equation (3.3) is nonlinear, because b depends on z, and has to be solved iteratively (e.g., with a Newton-Raphson procedure). At each iteration, an evaluation of b and of ∂ h∕∂ z has to be provided. If the nonlinearity is weak, in some cases f can be accurately approximated with a few number of harmonics N H , and analytical relations between the Fourier coefficients of the forces b and of the displacements z can be developed together with the expression of the jacobian of the system [15–17]. When such developments are too intricate, most of the studies in the literature propose to evaluate b through successive transformations from frequency to time domains. For example, the alternating frequency/time-domain (AFT) technique [18] takes advantage of the fast Fourier transform to compute b:

$$\displaystyle{ \mathbf{z}\mathop{\longrightarrow}\limits_{}^{{\mbox{ FFT}}^{-1}}\mathbf{x}(t)\mathop{\longrightarrow}\limits_{}^{}\mathbf{f}\left (\mathbf{x},\dot{\mathbf{x}},\omega,t\right )\mathop{\longrightarrow}\limits_{}^{\mbox{ FFT}}\mathbf{b}(\mathbf{z},\omega ) }$$
(3.5)

The jacobian matrix of the system then has to be computed through finite differences, which can be cumbersome in terms of CPU time, or through linearization of the equations [9].

An efficient alternative consists in rewriting the inverse Fourier transform as a linear operator Γ ω[19–22]. First, denoting N as the number of time samples of a discretized period of oscillation, one defines vectors \(\tilde{\mathbf{x}}\) and \(\tilde{\mathbf{f}}\) containing the concatenated nN time samples of the displacements and the forces, respectively, for all the DOFs:

$$\displaystyle{ \begin{array}{ccc} \tilde{\mathbf{x}} = \left [\begin{array}{c} x_{1}\left (t_{1}\right )\\ \vdots \\ x_{1}\left (t_{N}\right )\\ \vdots \\ x_{n}\left (t_{1}\right )\\ \vdots \\ x_{n}\left (t_{N}\right ) \end{array} \right ],&&\tilde{\mathbf{f}} = \left [\begin{array}{c} f_{1}\left (t_{1}\right )\\ \vdots \\ f_{1}\left (t_{N}\right )\\ \vdots \\ f_{n}\left (t_{1}\right )\\ \vdots \\ f_{n}\left (t_{N}\right ) \end{array} \right ] \end{array} }$$
(3.6)

The inverse Fourier transform can then be written as a linear operation:

$$\displaystyle{ \tilde{\mathbf{x}} =\boldsymbol{ \Gamma }\left (\omega \right )\mathbf{z} }$$
(3.7)

with the nN × 2N H + 1n sparse operator

$$\displaystyle{ \begin{array}{c} \boldsymbol{\Gamma }\left (\omega \right ) = \left [\begin{array}{cccccc} \mathbb{I}_{n} \otimes \left [\begin{array}{c} 1\\ 1\\ \vdots \\ 1 \end{array} \right ]&\mathbb{I}_{n} \otimes \left [\begin{array}{c} \sin \left (\omega t_{1}\right ) \\ \sin \left (\omega t_{2}\right )\\ \vdots \\ \sin \left (\omega t_{N}\right ) \end{array} \right ]&\mathbb{I}_{n} \otimes \left [\begin{array}{c} \cos \left (\omega t_{1}\right ) \\ \cos \left (\omega t_{2}\right )\\ \vdots \\ \cos \left (\omega t_{N}\right ) \end{array} \right ]&\mathop{\ldots }&\mathbb{I}_{n} \otimes \left [\begin{array}{c} \sin \left (N_{H}\omega t_{1}\right ) \\ \sin \left (N_{H}\omega t_{2}\right )\\ \vdots \\ \sin \left (N_{H}\omega t_{N}\right ) \end{array} \right ]&\mathbb{I}_{n} \otimes \left [\begin{array}{c} \cos \left (N_{H}\omega t_{1}\right ) \\ \cos \left (N_{H}\omega t_{2}\right )\\ \vdots \\ \cos \left (N_{H}\omega t_{N}\right ) \end{array} \right ] \end{array} \right ] \end{array} }$$
(3.8)

where ⊗ stands for the Kronecker tensor product. Figure 3.1 represents the inverse transformation matrix for the case n = 2, N = 64, and N H  = 5.

Fig. 3.1
figure 1

Illustration of the inverse Fourier transformation matrix Γ ω for n = 2, N = 64, and N H  = 5

Full size image

The direct Fourier transformation is written

$$\displaystyle{ \mathbf{z} ={ \left (\boldsymbol{\Gamma }\left (\omega \right )\right )}^{+}\tilde{\mathbf{x}} }$$
(3.9)

where+ stands for the Moore-Penrose pseudoinverse:

$$\displaystyle{ \boldsymbol{{\Gamma }}^{+} =\boldsymbol{ {\Gamma }}^{T}{\left (\boldsymbol{\Gamma }\boldsymbol{{\Gamma }}^{T}\right )}^{-1} }$$
(3.10)

According to these notations, the Fourier coefficients of the linear and nonlinear forces are simply obtained by transforming the signals in the time domain back to the frequency domain:

$$\displaystyle{ \mathbf{b}(\mathbf{z},\omega ) ={ \left (\boldsymbol{\Gamma }\left (\omega \right )\right )}^{+}\tilde{\mathbf{f}} }$$
(3.11)

The jacobian matrix of expression (3.3) with respect to the Fourier coefficients z can be computed as

$$\displaystyle{ \mathbf{J}_{z} = \frac{\partial \mathbf{h}} {\partial \mathbf{z}} = \mathbf{A} -\frac{\partial \mathbf{b}} {\partial \mathbf{z}} }$$
(3.12)

In order to compute the derivative of b with respect to the Fourier coefficients of the displacements, z, one can use the following chain rule:

$$\displaystyle{ \frac{\partial \mathbf{b}} {\partial \mathbf{z}} = \frac{\partial \mathbf{b}} {\partial \tilde{\mathbf{f}}} \frac{\partial \tilde{\mathbf{f}}} {\partial \tilde{\mathbf{x}}} \frac{\partial \tilde{\mathbf{x}}} {\partial \mathbf{z}} }$$
(3.13)

which can rewritten with the transformation matrices

$$\displaystyle{ \frac{\partial \mathbf{b}} {\partial \mathbf{z}} =\boldsymbol{ {\Gamma }}^{+} \frac{\partial \tilde{\mathbf{f}}} {\partial \tilde{\mathbf{x}}}\boldsymbol{\Gamma } }$$
(3.14)

In general, the derivatives of the forces with respect to the displacements in the time domain can be expressed analytically, which makes the computation of the jacobian matrix of (3.3) faster than with the finite differences.

3.2.2 Continuation Procedure

It is usually of interest to solve (3.3) for a range of parameter values ω, rather than for a single value of the parameter. One could for example be interested in the behavior of a structure in the neighborhood of a resonance peak. A continuation scheme, coupled to the highlighted HB method, has therefore to be implemented.

Solving (3.3) for different fixed values of ω, as done with a sequential continuation procedure, fails at turning point. To overcome this issue, for this work a procedure based on tangent predictions and Moore-Penrose corrections has been selected, as proposed in the software matcont.

Denoting J ω as the jacobian of h with respect to the parameter ω, the search for a tangent vector t (i) at an iteration point z (i), ω (i) along the branch reads

$$\displaystyle{ \left [\begin{array}{cc} \mathbf{J}_{z}& \mathbf{J}_{\omega } \\ {\mathbf{t}_{(i-1)}^{T}} \end{array} \right ]\mathbf{t}_{(i)}^{T} = \left [\begin{array}{c} \mathbf{0} \\ 1 \end{array} \right ] }$$
(3.15)

The last equation in the system (3.15), imposing a scalar product of 1 between the new tangent and the previous one prevents the continuation procedure from turning back. For the first iteration of the procedure, this last row can be replaced by a condition imposing the sum of the components of the tangent to be equal to 1.

The correction stage is based on Newton’s method. Introducing new optimization variables v (i, j) initialized as v (i, 1) = t (i), and y (i, j) = z (i, j) ω (i, j) T, the different Newton’s iterations i are constructed as following:

$$\displaystyle{ \begin{array}{l} \mathbf{y}_{(i,j+1)} = \mathbf{y}_{(i,j)} -\mathbf{G}_{y}^{-1}\left (\mathbf{y}_{(i,j)},\mathbf{v}_{(i,j)}\right )\mathbf{G}\left (\mathbf{y}_{(i,j)},\mathbf{v}_{(i,j)}\right ) \\ \mathbf{v}_{(i,j+1)} = \mathbf{v}_{(i,j)} -\mathbf{G}_{y}^{-1}\left (\mathbf{y}_{(i,j)},\mathbf{v}_{(i,j)}\right )\mathbf{R}\left (\mathbf{y}_{(i,j)},\mathbf{v}_{(i,j)}\right )\\ \end{array} }$$
(3.16)

with

$$\displaystyle{ \begin{array}{ccccc} \mathbf{G}\left (\mathbf{y},\mathbf{v}\right ) = \left [\begin{array}{c} \mathbf{h}\left (\mathbf{y}\right )\\ \mathbf{0} \end{array} \right ],&&\mathbf{G}_{y}\left (\mathbf{y},\mathbf{v}\right ) = \left [\begin{array}{c} \begin{array}{cc} \mathbf{J}_{z}\left (\mathbf{y}\right )&\mathbf{J}_{\omega }\left (\mathbf{y}\right ) \end{array} \\ {\mathbf{v}}^{T} \end{array} \right ],&&\mathbf{R}\left (\mathbf{y},\mathbf{v}\right ) = \left [\begin{array}{c} \left [\begin{array}{cc} \mathbf{J}_{z}\left (\mathbf{y}\right )&\mathbf{J}_{\omega }\left (\mathbf{y}\right ) \end{array} \right ]\mathbf{v}\\ \mathbf{0} \end{array}\right ] \end{array} }$$
(3.17)

For a more detailed presentation of the continuation procedure, the reader can refer to [6].

3.2.3 Stability Analysis

Bifurcation detection is usually related to the stability analysis of the solutions. The continuation procedure developed above does not indicate if a periodic solution is stable or not; therefore, a stability analysis has to be performed along the branch. In the case of time domain methods, such as the shooting technique, one usually obtains the monodromy matrix as a by-product of the procedure [2], which then provides the Floquet multipliers to study the stability of the solutions. On the other hand, in the case of frequency domain techniques such as the HB method, one preferably uses Hill’s method by solving a quadratic eigenvalue problem whose components are obtained as by-products of the method. The quadratic eigenvalue problem proposed by von Groll et al. [10] for finding the Hill’s coefficients as solutions of

$$\displaystyle{ \boldsymbol{\Delta }{_{2}\boldsymbol{\lambda }}^{2} +\boldsymbol{ \Delta }_{ 1}\boldsymbol{\lambda } + \mathbf{J}_{z} = \mathbf{0} }$$
(3.18)

with

$$\displaystyle{ \begin{array}{ccc} \boldsymbol{\Delta }_{1} = \left [\begin{array}{cccc} \mathbf{C}& && \\ &\begin{array}{cc} \mathbf{C} & - 2\frac{\omega }{\nu }\mathbf{M} \\ 2\frac{\omega }{\nu }\mathbf{M}& \mathbf{C} \end{array} && \\ & &\ddots & \\ & &&\begin{array}{cc} \mathbf{C} & - 2N_{H}\frac{\omega } {\nu }\mathbf{M}\\ 2N_{ H}\frac{\omega } {\nu }\mathbf{M}& \mathbf{C} \end{array} \end{array} \right ],&&\boldsymbol{\Delta }_{2} = \mathbb{I}_{\left (2N_{H}+1\right )} \otimes \mathbf{M} \end{array} }$$
(3.19)

can be rewritten as a linear eigenvalue problem of double size

$$\displaystyle{ \mathbf{B}_{1}-\left [\begin{array}{c} \boldsymbol{\lambda }\\ \\ \boldsymbol{\gamma } \end{array} \right ]\mathbf{B}_{2} = \mathbf{0} }$$
(3.20)

with

$$\displaystyle{ \begin{array}{ccc} \mathbf{B}_{1} = \left [\begin{array}{cc} \boldsymbol{\Delta }_{1} &\mathbf{J}_{z} \\ - \mathbb{I}& \mathbf{0} \end{array} \right ],&&\mathbf{B}_{2} = -\left [\begin{array}{cc} \boldsymbol{\Delta }_{2}&\mathbf{0}\\ \mathbf{0} &\mathbb{I} \end{array} \right ] \end{array} }$$
(3.21)

The eigenvalues λ can thus be found among the eigenvalues of the matrix

$$\displaystyle{ \mathbf{B} = \mathbf{B}_{2}^{-1}\mathbf{B}_{ 1} }$$
(3.22)

As will be explained in Sect. 3.2.4, the matrix B has a key role in the detection and tracking of bifurcations. After sorting the obtained eigenvalues in order to eliminate the numerical ones, as proposed by Lazarus et al. [23], one can directly relates the remaining eigenvalues λ ∗ to the Floquet exponents. The term “Floquet exponents” will be used throughout this paper; it should however be kept in mind that these exponents are computed with the Hill’s method.

3.2.4 Detection and Tracking of Bifurcations

In this work the detection and tracking of LPs and NSs is sought, based on the Floquet exponents. A LP bifurcation is detected when a Floquet exponent cross the imaginary axis along the real axis. It can also be detected when the component of the tangent prediction related to the parameter ω changes sign. As a consequence, the jacobian matrix J z is singular at a LP bifurcation. In order to continue a LP bifurcation with respect to a parameter of the system, one has to append one equation to (3.3). A condition imposing the singularity of the jacobian matrix is often used:

$$\displaystyle{ \left \vert \mathbf{J}_{z}\right \vert = 0 }$$
(3.23)

Nevertheless, under this form the extra equation could lead to scaling problems. To overcome this issue, Doedel et al. [24] proposed the use of the so-called bordering technique. The idea of this technique is to use an extra equation of the form

$$\displaystyle{ g_{LP} = 0 }$$
(3.24)

with g LP a scalar function which vanishes simultaneously with the determinant of J z . Such a function can be obtained by solving

$$\displaystyle{ \left [\begin{array}{cc} \mathbf{J}_{z} &\mathbf{p}_{LP} \\ \mathbf{q}_{LP}^{{\ast}}& 0 \end{array} \right ]\left [\begin{array}{c} \mathbf{w}\\ g_{ LP} \end{array} \right ] = \left [\begin{array}{c} \mathbf{0}\\ 1 \end{array} \right ] }$$
(3.25)

where∗ denotes a conjugate transpose, and where p LP and q LP are chosen to ensure the nonsingularity of the matrix.

The second type of bifurcation studied in this paper, the NS bifurcation, is detected when a pair of Floquet exponents cross the imaginary axis as a pair of complex conjugates. Using the theory of the bialternate matrix product [25] P ⊙ of a m × m matrix P

$$\displaystyle{ \mathbf{P}_{\odot } = \mathbf{P} \odot \mathbb{I}_{m} }$$
(3.26)

which has the property to be singular when P has a pair of complex conjugates crossing the imaginary axis, one can develop the following extra equation to track a NS bifurcation:

$$\displaystyle{ \left \vert \mathbf{B}_{\odot }\right \vert = 0 }$$
(3.27)

or, by using the bordering techniques as in (3.25):

$$\displaystyle{ g_{NS} = 0 }$$
(3.28)

with g NS obtained by solving

$$\displaystyle{ \left [\begin{array}{cc} \mathbf{B}_{\odot } &\mathbf{p}_{NS} \\ \mathbf{q}_{NS}^{{\ast}}& 0 \end{array} \right ]\left [\begin{array}{c} \mathbf{w}\\ g_{ NS} \end{array} \right ] = \left [\begin{array}{c} \mathbf{0}\\ 1 \end{array} \right ] }$$
(3.29)

where p NS and q NS are chosen to ensure the nonsingularity of the matrix.

3.3 Validation of the Method on the Study of an Industrial, Complex Model with Strong Nonlinearities: The Smallsat

In this section, the HB method is used to address the continuation of periodic solutions for a large-scale structure and the detection of their bifurcations. In addition, the study will illustrate how one can take advantage of the filtering features of the method to efficiently compute normal modes of the structure.

3.3.1 Case Study

The example studied is referred to as the SmallSat, a structure represented in Fig. 3.2 and which was conceived by EADS-Astrium as a platform for small satellites. The interface between the spacecraft and launch vehicle is achieved via four aluminum brackets located around cut-outs at the base of the structure. The total mass of the spacecraft including the interface brackets is around 64 kg, it is 1.2 m in height and 1 m in width. It supports a dummy telescope mounted on a baseplate through a tripod, and the telescope plate is connected to the SmallSat top floor by three shock attenuators, termed shock attenuation systems for spacecraft and adaptor (SASSAs), whose dynamic behavior may exhibit nonlinearity.

Fig. 3.2
figure 2

SmallSat spacecraft equipped with an inertia wheel supported by the WEMS device and a dummy telescope connected to the main structure by the SASSA isolators

Full size image

Besides, as depicted in Fig. 3.3a, a support bracket connects to one of the eight walls the so-called wheel elastomer mounting system (WEMS) device which is loaded with an 8-kg dummy inertia wheel. The WEMS device is a mechanical filter which mitigates disturbances coming from the inertia wheel through the presence of a soft elastomeric interface between its mobile part, i.e. the inertia wheel and a supporting metallic cross, and its fixed part, i.e. the bracket and by extension the spacecraft. Moreover, eight mechanical stops limit the axial and lateral motions of the WEMS mobile part during launch, which gives rise to strongly nonlinear dynamical phenomena. A thin layer of elastomer placed onto the stops is used to prevent metal-metal impacts. Figure 3.3b presents a simplified though relevant modelling of the WEMS device where the inertia wheel, owing to its important rigidity, is seen as a point mass. The four nonlinear connections (NCs) between the WEMS mobile and fixed parts are labelled NC 1–4. Each NC possesses a trilinear spring in the axial direction (elastomer in traction/compression plus two stops), a bilinear spring in the radial direction (elastomer in shear plus one stop) and a linear spring in the third direction (elastomer in shear). In Fig. 3.3b, linear and nonlinear springs are denoted by squares and circles, respectively.

Fig. 3.3
figure 3

WEMS device. (a) Detailed description of the WEMS components, (b) simplified modeling of the WEMS mobile part considering the inertia wheel as a point mass. The linear and nonlinear connections between the WEMS mobile and fixed parts are signaled by open square and open circle, respectively

Full size image

A finite element model (FEM) of the SmallSat was developed and used in the present work to conduct numerical experiments. It comprises about 150,000 DOFs and the comparison with experimental data revealed its good predictive capabilities. The model consists of shell elements (octagon structure and top floor, instrument baseplate, bracket and WEMS metallic cross) and point masses (dummy inertia wheel and telescope) and meets boundary conditions with four clamped nodes. Proportional damping is considered and the high dissipation in the elastomer components of the WEMS is described using lumped dashpots, hence resulting in a highly non-proportional damping matrix. Then, to achieve tractable nonlinear calculations, the linear elements of the FEM were condensed using the Craig-Bampton reduction technique. This approach consists in expressing the system dynamics in terms of some retained DOFs and internal modes of vibration. Specifically, the full-scale model of the spacecraft was reduced to 8 nodes (excluding DOFs in rotation), namely both sides of each NC, and 10 internal modes. In total, the reduced-order model thus contains 34 DOFs. Bilinear and trilinear springs were finally introduced within the WEMS module between the NC nodes to model the nonlinearities of the connections between the WEMS and the rest of the SmallSat [26]. To avoid numerical issues, regularization with third-order polynomials was utilized in the close vicinity of the clearances to implement C 1 continuity.

3.3.2 Study of the Normal Modes

Because of the presence of the nonlinearities, this model has a feature typical of nonlinear systems: its oscillations are frequency-energy dependent. In order to assess this dependence, one can use the framework of Nonlinear Normal Modes (NNMs) as proposed by Vakakis et al. [27], and Kerschen et al. [28]. The concept of NNM can be seen as a nonlinear generalization of the concept of Linear Normal Mode (LNM) of classical linear vibration theory. It was originally defined by Lyapunov [29] and Rosenberg [30], its definition being then extended to the following: a NNM is a (nonnecessarily synchronous) periodic motion of the conservative system. In order to describe a NNM, one thus has to provide an initial state for the system (displacements and velocities) whose free response leads to periodic oscillation of the DOFs with a dominant frequency ω. Since the system is conservative, the total (kinetic and potential) energy level E related to its state does not evolve during the simulation.

A convenient tool to depict the NNMs, the Frequency-Energy Plot (FEP), consists in representing the evolution of the frequency ω with respect to the energy level E. This procedure facilitates the identification of families of NNMs sharing the same qualitative properties (a global in-phase motion for example). The FEP depicted in Fig. 3.4a shows the fifth family of NNMs of the underlying undamped model of the SmallSat, computed with the shooting technique. Analyzing that branch for low energy levels, for which the oscillations have small amplitudes and do not activate the nonlinearities since the metallic cross does not interact with the mechanical stops, one notices that the frequency of the NNMs does almost not depend on E; it can be shown to be the same as the frequency of the LNM of the underlying linear system. For larger levels of E, the dynamics of the system changes because of the participation of the nonlinearities. This change is sudden, which is a consequence of the nonsmooth property of the bilinear and trilinear springs. The frequency of the NNMs increases as a function of E; the positive stiffness of the nonlinear springs explains this hardening behavior of the system.

Fig. 3.4
figure 4

Analysis of the fifth NNM of the SmallSat. (a) Shooting, (b) HB method with N H  = 1, (c) N H  = 3, (d) N H  = 5

Full size image

A closer look on frequencies above 22.5 Hz in Fig. 3.4a highlights another feature of nonlinear systems: the internal resonances between the nonlinear modes. Because the fifth NNM branch does not have the same dependence in energy as the other NNM branches, in some regions these branches can have commensurate frequencies. For example, in the case of a 2:1 resonance, the fifth NNM branch has a frequency which is exactly two times smaller than the frequency of another NNM branch. Because a solution 2ω-periodic is also ω-periodic, the two modes interact and the periodic solutions resulting from this interaction appears as a small part, termed tongue, emanating from the main branch, called backbone, in the FEP. Four different internal resonances are depicted in Fig. 3.4a, namely 2:1, 4:1, 15:1 and 120:1. However, it can be demonstrated that there generally exist a countable infinity of such internal resonances for nonlinear systems [28].

Some practical issues emerge from this peculiar property. The computation of the tongues can be slow and intricate because of the complex dynamics involved in such regions. Moreover, one can encounter many tongues during the continuation procedure, while the user is maybe only interested in the global behavior of the branch. Due to the large number of DOFs and internal modes in the model of the SmallSat, giving a large number of mode interactions, the density of internal resonances is high and the resonances are very close to each other in the FEP for this example. If only the global behavior of the backbone of the mode is of interest for the user, this clearly represents an issue in terms of computation time since most of this time is spent to compute the internal resonances.

For these reasons, a continuation algorithm coupled with the HB method is interesting in the sense that, by truncating the Fourier series to a certain number of harmonics, one controls the internal resonances that can be approximated. Figure 3.4b–d depict this low-pass filtering effect on the fifth mode of the SmallSat for three numbers of harmonics retained in the Fourier series: 1, 3 and 5 respectively. Interestingly enough, one first notices that the branch with 1 harmonic, although it ignores all the internal resonances and although the nonlinearities are strong, accurately describes the global trend of the backbone. Adding harmonics to the method up to the 3rd order enables it to approximate the 2:1 resonance tongue, while higher order resonances are not detected. Continuing the branch with 5 harmonics also indicates the presence of the 4:1 resonances. However, increasing the number of harmonics in the Fourier series implies an increase of the size of the system (3.3) and thereby an increase of the computation time. There is thus a tradeoff between the computation speed and the desired accuracy of the solutions, in terms of the number of harmonics represented.

3.3.3 Study of the Forced Response

The second part of the study of the SmallSat is carried out on the forced response of the structure for a vertical harmonic excitation on the DOF of the inertia wheel. For this purpose, an additional node related to the inertia wheel is added to the reduced finite element model; this model now comprises 37 DOFs. A forcing amplitude of 140 N is considered, and the amplitude of the response of the vertical (Z) component of the NC 1 node is studied.

Figure 3.5a depicts the frequency response of the system computed with a shooting technique, with the LP and NS bifurcations detected. This branch is considered as the reference solution. Figure 3.5b represents the same frequency response, computed with the HB method for N H  = 5. In spite of the presence of strong nonlinearities in the system, one observes that the responses with 5 or more harmonics accurately approximate the reference solution; the same conclusions can also be drawn about the detection of LP and NS bifurcations.

Fig. 3.5
figure 5

Frequency response of the NC1-Z node of the SmallSat for a harmonic excitation of 140N applied to the inertia wheel. (a) Shooting, (b) HB method with N H  = 5. The solid line is obtained with the HB method and the dashed line is obtained with the shooting technique. Markers cross and inverted filled triangle depict LP and NS bifurcations, respectively, detected with a study of the monodromy matrix, and markers filled circle and filled triangle depict LP and NS bifurcations, respectively, detected with Hill’s method

Full size image

To understand the influence of bifurcations such as NS points, Fig. 3.6a,b give the time series of the NC1-Z node of the SmallSat obtained from a time integration with a Newmark scheme for a harmonic excitation of 140 N applied to the inertia wheel, with frequencies of 29.5 and 30.3 Hz respectively. While the first excitation regime, located before a NS bifurcation in the frequency response of Fig. 3.5, gives a periodic oscillation of the structure, the second regime, located after that NS bifurcation, leads to an enrichment of the response spectrum and to the emergence of quasiperiodic solutions. Crossing a bifurcation, even for a small frequency variation, can thus drastically alter the dynamics of nonlinear systems. This example illustrates the importance of the detection of these bifurcations when analyzing and designing a mechanical structure.

Fig. 3.6
figure 6

Time series of the NC1-Z node of the SmallSat for a harmonic excitation of 140 N applied to the inertia wheel. (a) ω = 29. 5 Hz, (b) ω = 30. 3 Hz

Full size image

3.4 Bifurcation Tracking Coupled to the Harmonic Balance Method

In addition to the computation of periodic solutions, the HB method can also exploit the important information contained in the bifurcations by tracking them in a parameter space. Here we propose to use the HB method not only to model a nonlinear behavior but also to exploit it constructively as a design tool, with an application to a nonlinear vibration absorber.

3.4.1 Case Study

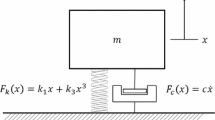
In this section, the performance of a Nonlinear Tuned Vibration Absorber (NLTVA) attached to a harmonically forced 1DOF host structure is studied. The motion of this system represented in Fig. 3.7 is governed by the equations

$$\displaystyle\begin{array}{rcl} & & m\ddot{x}_{1} + c\dot{x}_{1} + c_{abs}\left (\dot{x}_{1} -\dot{ x}_{2}\right ) + k_{l}x_{1} + k_{l,abs}\left (x_{1} - x_{2}\right ) + k_{nl}x_{1}^{3} + k_{ nl,abs}{\left (x_{1} - x_{2}\right )}^{3} = F\cos \left (\omega t\right ) \\ & & \quad \epsilon m\ddot{x}_{2} + c_{abs}\left (\dot{x}_{2} -\dot{ x}_{1}\right ) + k_{l,abs}\left (x_{2} - x_{1}\right ) + k_{nl,abs}{\left (x_{2} - x_{1}\right )}^{3} = 0 {}\end{array}$$
(3.30)

where the parameters of the host structure are m = 1, c = 0. 002, k l  = 1 and k nl  = 1. The parameters of the absorber are determined as follows:

  • In order to account for practical limitations, the mass of the NLTVA is chosen as 5% of the mass of the host structure:

    $$\displaystyle{\epsilon = 0.05}$$

  • The linear stiffness and damping are chosen according to a linear tuning rule, such as the Den Hartog’s equal peak method [31]. This ensures performance of the NLTVA as good as for a linear TVA, for low energy levels. The equal peak method gives

    $$\displaystyle{\begin{array}{cc} c_{abs} = 0.013,&k_{l,abs} = 0.0453\\ \end{array} }$$

  • The nonlinear stiffness coefficient is determined to ensure the equal peak criterion for a large range of forcing amplitudes (see [32] for more details):

    $$\displaystyle{k_{nl,abs} = 0.0042}$$
Fig. 3.7
figure 7

Schematic representation of the 1DOF+NLTVA system

Full size image

3.4.2 Tracking of LP and NS Bifurcations

The main frequency response of the host structure is depicted in Fig. 3.8 for a forcing amplitude of F = 0. 13. Three responses are given: the first one is computed with HB method and N H  = 1, the second one with N H  = 5 and the last one is computed with the orthogonal collocation technique (using matcont package), which is here considered as the reference solution. The approximation with only one harmonic retained gives satisfactory results, while the approximation with five harmonics is almost coincident with the reference solution.

Fig. 3.8
figure 8

Main frequency response of the host structure of the 1DOF+NLTVA system, for F = 0. 13. Comparison between the HB method (N H  = 1 and N H  = 5) and the orthogonal collocation method

Full size image

In addition to the main frequency response, a global analysis of the dynamics of the system reveals the presence of an isolated solution, as shown in Fig. 3.9a, which cannot be directly tracked from the main part. In order to be able to detect such isolas with a continuation procedure based on HB method, one can take advantage of the tracking of the LP bifurcations in the codimension-2 parameter space ω, F, with the amplitude of the oscillations of x 1 as representation of the state of the system. A projection of the LP branch on the ω-amplitude plane is given in Fig. 3.9c for N H  = 5, together with the detection of the LPs in the frequency response of the main structure for F = 0. 13 and F = 0. 19 (Fig. 3.9a,b, respectively). The LP branches computed with the orthogonal collocation technique, represented in Fig. 3.9c with cross markers, confirm the accuracy of the solutions computed with the HB method.

Fig. 3.9
figure 9

LP tracking for the host structure of the 1DOF+NLTVA system. (a) Frequency response and LP detection for F = 0. 13, (b) Frequency response and LP detection for F = 0. 19, (c) Projection of the LP branch on the ω-amplitude plane. The solid lines are obtained with the HB method with N H  = 5 and the cross markers are obtained with the orthogonal collocation method. The markers filled circle highlight LPs at the forcing amplitudes of interest, and the marker open square denotes the turning point indicating the merging of the isola with the main frequency response

Full size image

Fixing the forcing amplitude to F = 0. 13 in Fig. 3.9c, one finds four solutions on the LP branches which indicates the presence of four LP bifurcations as verified in Fig. 3.9a. The same observation can be made with the four LP bifurcations in Fig. 3.9b. By starting the bifurcation tracking from a LP on the main frequency response, one can thus detect the presence of isolas and regions of large oscillation that would be missed by a simple study of the main frequency response. These branches of LP bifurcations are therefore interesting tools for the study of the global dynamics of the system.

As the amplitude of the forcing applied to the host structure rises, the isola grows and finally merges with the main frequency response, causing a steep increase for the maximal amplitude of the main frequency response and thereby the detuning of the NLTVA. Interestingly, this phenomenon can also be detected through the presence of the turning point on the LP branch depicted in Fig. 3.9c with a square marker, indicating the merging and elimination of two LP bifurcations around F = 0. 181, the first one being related to the main frequency response and the second one being related to the isola. In the perspective of a tuning procedure for the NLTVA, the position of this merging point in the parameter space is crucial because it indicates when the detuning of the absorber occurs. By varying other parameters such as the damping coefficient c abs , it is interesting to observe the behavior of this point in order to delay the detuning phenomenon to higher forcing amplitudes; the performance analysis of the NLTVA and its optimization is however beyond the scope of this paper.

The analysis is now carried out for the detection and tracking of NS bifurcations. Figure 3.10a,b depict the frequency response of the host structure for a forcing amplitude of F = 0. 14 and F = 0. 19 respectively, together with the NS bifurcations detected along that branch, for N H  = 1. The tracking of NS bifurcations is represented in Fig. 3.10c for N H  = 1 and a comparison with the branch computed with the orthogonal collocation technique is also provided. Interestingly enough, the merging of the main frequency response with the isola can also be predicted with the NS branch, through the elimination of two NS bifurcations around F = 0. 197. Moreover, because the NS bifurcations could cause the presence of quasiperiodic solutions of high amplitude, one could advantageously control their position by utilizing the NS tracking as a design tool. As far as the accuracy of the approximation is concerned, one observes that, although it is negligible for small amplitudes of the response, the difference between the HB method with N H  = 1 and the orthogonal collocation technique increases when this amplitude gets larger. It would be interesting to perform the same computation with more harmonics; nevertheless, the presence of numerical eigenvalues in B complicates the computation for N H  > 1. This challenge requires further investigation and is left to future work.

Fig. 3.10
figure 10

NS tracking for the host structure of the 1DOF+NLTVA system. (a) Frequency response and NS detection for F = 0. 14, (b) Frequency response and NS detection for F = 0. 19, (c) Projection of the NS branch on the ω-amplitude plane. The solid lines are obtained with the HB method with N H  = 1 and the cross markers are obtained with the orthogonal collocation method. The markers filled triangle highlight NSs at the forcing amplitudes of interest

Full size image

3.5 Conclusions

This paper intended to extend the theory of the harmonic balance method, originally limited to the continuation of periodic solutions, to a practical tool for the analysis and design of mechanical systems. First, it was shown to be appropriate for calculating the frequency responses and the nonlinear normal modes of a large-scale structure involving strong nonlinearities, thanks its inherent filtering feature. Through its extensions to detect and track limit point and Naimark-Sacker bifurcations, the HB method was also proved useful for detecting other types of solution such as isolas and quasiperiodic oscillations. The last part of the paper illustrated the utilization of the method as an optimization tool to develop a robust nonlinear vibration absorber. Both applications revealed the efficiency of these extensions of the HB method even for a low number of harmonics considered.