Keywords

12.1 Introduction

Combinations of vibro-impact nonlinearities and nonlinear springs are found in several technical systems like for example hammer drills. In this paper some methods are discussed for the simulation of these systems. The modeling of the vibro-impact system which is used in the following calculations is described in Sect. 12.2. Subsequently, the work focuses on the calculation of Frequency Response Functions (FRF) which are basic for the characterization of the dynamic behavior of the presented systems. For vibro-impact systems FRFs can be utilized for the estimation of maximum amplitudes at certain frequencies as well as to indicate branches with multiple solutions. The Harmonic Balance Method (HBM) is used under consideration of higher and subharmonic influences to calculate FRFs of vibro-impact systems with and without additional cubic nonlinearity. The fundamentals of the HBM considering higher and subharmonic influence are introduced in Sect. 12.3. However, some typical features of vibro-impact systems can make such calculations troublesome. Especially the solution method has to be adapted due to characteristic of the impact force. Moreover, capturing the occurrence of multiple solutions in certain frequency ranges is a challenging task for the systems regarded in this paper. To solve this problem a continuation method is applied which is described briefly in Sect. 12.3. Although this approach allows the calculation of FRFs of complex nonlinear systems, it is not sufficient to capture their overall dynamics. Particularly in vibro-impact systems aperiodic or chaotic motions are likely to appear. This fact is treated separately in Sect. 12.4 by the calculation of Lyapunov-Exponents and visualized with phase portraits and Poincaré-Sections. Some numerical results for the methods mentioned above are discussed in Sect. 12.5. The paper closes with the conclusion and suggestions for future research.

12.2 Vibro-Impact System Representation

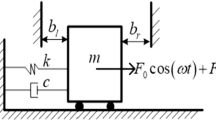
There are numerous methods for the modeling of impacts in mechanical systems [1] and some of the results remarkably depend on the modeling [2]. However, a comparable study of different types of modeling of the impact goes beyond the scope of this work. In this paper the impact is represented by a spring-damper combination in which the stiffness k 0 represents the stiffness of the impact and the damper constant d 0 represents the energy dissipation due to impact. Figure 12.1 displays the setup for a Single-Degree-Of-Freedom (SDOF)-Oscillator under harmonic excitation. Apart from a linear spring with stiffness k and linear damper element with damping constant d a cubic spring is included.

Fig. 12.1
figure 1

SDOF-Oscillator with cubic spring and one-sided impact

Full size image

The cubic spring stiffness β can either represent a progressive behavior for β > 0 or a degressive behavior for β < 0. Generally, the equation of motion can be written as

$$\displaystyle{ m\ddot{x} + d\dot{x} + kx + F_{\mathrm{nl}}(\dot{x},x,t) = F_{\mathrm{exc}} }$$
(12.1)

with the nonlinear force \(F_{\mathrm{nl}}(\dot{x},x,t)\) as a sum of the cubic spring force

$$\displaystyle{ F_{cub} =\beta {x}^{3} }$$
(12.2)

and the impact force which is a non-smooth function depending on the distance between the mass and the location of the impact denoted by z 0

$$\displaystyle{ F_{imp} = \left \{\begin{array}{@{}l@{\quad }l@{}} \quad 0 \quad &x < z_{0} \\ \:-k_{0}(x - z_{0}) - d_{0}\dot{x}\quad &x \geq z_{0}. \end{array} \right. }$$
(12.3)

Within this contribution the presented oscillator is used with different sets of parameters in order to show the occurrence of harmonics depending on the used nonlinearity. Additionally, the influence of combined nonlinearities on the harmonics can be shown.

12.3 Harmonic Balance Method for Sub- and Higher Harmonic Response

The HBM is a method to approximately compute the steady state response of nonlinear systems [3, 4]. The method is based on the assumption that every nonlinear steady state response of a system which is driven by an excitation frequency ω can be expressed by a Fourier series with an infinite number of harmonics of this frequency. In its original version only the fundamental response is considered such that the method represents a rough approximation. For a consideration of a higher and subharmonic response like it is done in this contribution the underlying ansatz must be extended to

$$\displaystyle{ x(t) = a_{0} +\sum _{ \nu =1}^{\infty }\sum _{ \mu =1}^{\infty }a_{\nu /\mu }\cos \bigg(\frac{\nu } {\mu }\omega t\bigg) + b_{\nu /\mu }\sin \bigg(\frac{\nu } {\mu }\omega t\bigg). }$$
(12.4)

This ansatz now takes higher harmonics into account for ν > 1 and subharmonics are represented by μ > 1. The constant part a 0 considers the mean position of the vibration which is necessary for the investigated systems here. Note, that with this ansatz only harmonics in a rational condition are respected. Linear combinations of the harmonics to represent combination resonances [5] are not considered here since the excitation for the presented system is excited with only one frequency. In practice, the choice of the dominant harmonics is an important issue for the efficient calculation of FRFs finding a good trade-off between accuracy and computational cost. In some cases applying a Fast Fourier or Wavelet Transformation to the time signal helps to find dominant harmonics.

By having the ansatz for the response from Eq. (12.4) the nonlinear forces \(F_{\mathrm{nl}}(\dot{x},x,t)\) in Eq. (12.1) can be developed in a Fourier series

$$\displaystyle{ F_{\mathrm{nl}}(\dot{x},x,t) = A_{0} +\sum _{ \nu =1}^{\infty }\sum _{ \mu =1}^{\infty }A_{\nu /\mu }\cos \bigg(\frac{\nu } {\mu }\omega t\bigg) + B_{\nu /\mu }\sin \bigg(\frac{\nu } {\mu }\omega t\bigg), }$$
(12.5)

where the Fourier coefficients are determined by the following integrals

$$\displaystyle\begin{array}{rcl} A_{0}& =& \frac{1} {\mu T}\int _{0}^{\mu T}F_{\mathrm{ nl}}(\dot{x},x,t)\ \mathrm{dt}, \\ A_{\nu /\mu }& =& \frac{2} {\mu T}\int _{0}^{\mu T}F_{\mathrm{ nl}}(\dot{x},x,t)\cos \bigg(\frac{\nu } {\mu }\omega t\bigg)\ \mathrm{dt}, \\ B_{\nu /\mu }& =& \frac{2} {\mu T}\int _{0}^{\mu T}F_{\mathrm{ nl}}(\dot{x},x,t)\sin \bigg(\frac{\nu } {\mu }\omega t\bigg)\ \mathrm{dt}.{}\end{array}$$
(12.6)

For the calculation of these coefficients, the regarded period length T = 2π∕ω has to have at least the length of one full period, also for the subharmonic terms which have μ-times the period length of the excitation. Using an infinite number of these coefficients, the nonlinear force is approximated by

$$\displaystyle{ F_{\mathrm{nl}}(\dot{x},x,t) \approx A_{0} +\sum _{ \nu =1}^{\nu _{h} }\sum _{\mu =1}^{\mu _{h} }A_{\nu /\mu }\cos \bigg(\frac{\nu } {\mu }\omega t\bigg) + B_{\nu /\mu }\sin \bigg(\frac{\nu } {\mu }\omega t\bigg). }$$
(12.7)

Introducing complex values the nonlinear force can be written as complex valued amplitudes denoted by the hat symbol,

$$\displaystyle\begin{array}{rcl} F_{\mathrm{nl}}(\dot{x},x,t)& \approx & Re\Big(\hat{F}_{\mathrm{nl,0}} +\sum _{ \nu =1}^{\nu _{h} }\sum _{\mu =1}^{\mu _{h} }\big(\hat{F}_{\mathrm{nl,}\nu /\mu }\ {e}^{i\frac{\nu _{h}} {\mu _{h}}\omega t}\big)\Big) \\ & =& Re\Big(A_{\mathrm{0}} +\sum _{ \nu =1}^{\nu _{h} }\sum _{\mu =1}^{\mu _{h} }(A_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} - i\ B_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}})\ {e}^{i\frac{\nu _{h}} {\mu _{h}}\omega t}\Big).{}\end{array}$$
(12.8)

Considering steady state behavior, the time dependency can be canceled and the system of equations can be arranged in matrix form in the frequency domain as

$$\displaystyle\begin{array}{rcl} & & \underbrace{\mathop{\left [\begin{array}{*{10}c} k& 0 & 0 &0& 0 &0& 0\\ 0 &H_{ \mathrm{lin,1/1}} & 0 &0& 0 &0& 0 \\ 0 & 0 &H_{\mathrm{lin,1/2}} & 0& 0 &0& 0 \\ 0 & 0 & 0 & \ddots & 0 &0& 0\\ 0 & 0 & 0 &0 &H_{ \mathrm{lin,1/}\mu _{\mathrm{h}}} & 0& 0 \\ 0 & 0 & 0 &0& 0 & \ddots & 0\\ 0 & 0 & 0 &0 & 0 &0 &H_{ \mathrm{lin,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} \end{array} \right ]}}\limits _{\boldsymbol{H}_{\mathrm{lin,}\nu _{ \mathrm{h}}/\mu _{\mathrm{h}}}}\underbrace{\mathop{ \left [\begin{array}{*{10}c} \hat{x}_{0} \\ \hat{x}_{1/1} \\ \hat{x}_{1/2}\\ \vdots \\ \hat{x}_{\mathrm{1/}\mu _{\mathrm{h}}}\\ \vdots \\ \hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} \end{array} \right ]}}\limits _{\boldsymbol{\hat{x}}_{\nu _{\mathrm{ h}}/\mu _{\mathrm{h}}}} +\underbrace{\mathop{ \left [\begin{array}{*{10}c} \hat{F}_{\mathrm{nl,0}}(\hat{x}_{\mathrm{0}},\hat{x}_{\mathrm{1/2}},\mathop{\ldots },\hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}) \\ \hat{F}_{\mathrm{nl,1/1}}(\hat{x}_{\mathrm{0}},\hat{x}_{\mathrm{1/2}},\mathop{\ldots },\hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}) \\ \hat{F}_{\mathrm{nl,1/2}}(\hat{x}_{\mathrm{0}},\hat{x}_{\mathrm{1/2}},\mathop{\ldots },\hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}})\\ \vdots \\ \hat{F}_{\mathrm{nl,1}/\mu _{\mathrm{h}}}(\hat{x}_{\mathrm{0}},\hat{x}_{\mathrm{1/2}},\mathop{\ldots },\hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}})\\ \vdots \\ \hat{F}_{\mathrm{nl,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}(\hat{x}_{\mathrm{0}},\hat{x}_{\mathrm{1/2}},\mathop{\ldots },\hat{x}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}})\\ \end{array} \right ]}}\limits _{\boldsymbol{\hat{f}}_{\mathrm{nl,}\nu _{ \mathrm{h}}/\mu _{\mathrm{h}}}\big(\boldsymbol{\hat{x}}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}\big)} =\underbrace{\mathop{ \left [\begin{array}{*{10}c} & \hat{F}_{\mathrm{exc,0}} \\ & \hat{F}_{\mathrm{exc,1/1}} \\ & \hat{F}_{\mathrm{exc,1/2}}\\ & \vdots \\ & \hat{F}_{\mathrm{exc,1/}\mu _{\mathrm{h}}}\\ & \vdots \\ & \hat{F}_{\mathrm{exc,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} \end{array} \right ]}}\limits _{\boldsymbol{\hat{f}}_{\mathrm{exc},\nu _{ \mathrm{h}}/\mu _{\mathrm{h}}}},{}\end{array}$$
(12.9)
$$\displaystyle{ \text{with}\quad H_{\mathrm{lin},\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} = k + i\ \Big(\frac{\nu _{h}} {\mu _{h}}\omega \Big)d -\Big {(\frac{\nu _{h}} {\mu _{h}}\omega \Big)}^{2}m. }$$
(12.10)

Equation (12.10) represents the dynamic stiffness matrix of the SDOF system presented in Sect. 12.2 in a scalar form.

12.3.1 Solution Method

For the solution of the nonlinear system given in Eq. (12.9) the equations are transformed in an implicit form such that a residual has be iterated to zero,

$$\displaystyle{ \boldsymbol{r}(\boldsymbol{\hat{x}}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}) =\boldsymbol{ H}_{\mathrm{lin,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}\boldsymbol{\hat{x}}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}} +\boldsymbol{\hat{ f}}_{\mathrm{nl,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}(\boldsymbol{\hat{x}}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}) -\boldsymbol{\hat{ f}}_{\mathrm{exc,}\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}\mathop{ =}\limits^{!}\boldsymbol{0}. }$$
(12.11)

For this task a combination of a tangent prediction and a corrector step is used in the present case. The corrector step can be interpreted as a minimization problem of the form [6]

$$\displaystyle{ min\left \{\left \vert \boldsymbol{x} -\boldsymbol{ x}_{p(n+1)}\right \vert;\boldsymbol{r}(\boldsymbol{\hat{x}}_{\nu _{\mathrm{h}}/\mu _{\mathrm{h}}}) =\boldsymbol{ 0}\right \}. }$$
(12.12)

This means that the point on the curve is found which is closest to the predicted value. Figure 12.2 gives an overview on the used algorithm.

Fig. 12.2
figure 2

Predictor-Corrector algorithm overview

Full size image

Generally, a Gauss-Newton method is used for correction until an acceptable residuum ε acc is reached. This method provides super-linear convergence properties [7] and is quite robust as the predicted values are already near the solution. However, the solution of vibro-impact problems requires a more sophisticated algorithm as numerical problems appear due to the non-smoothness of the nonlinear force. Therefore, a Levenberg-Marquardt like procedure is used whenever the residuum is increasing at correction step k + 1 compared to the previous one k [8].

Furthermore, the control of the step size for the prediction step is a key factor to achieve both, robustness and reasonable computational cost. In this case the step size is controlled by a desired number of iterations k opt along with a multi-level trial and error method. This approach is advantageous in case of strong and sudden changes in the FRF [9] such as sharp bends caused by an impact.

Figure 12.2 (right) gives an example of a FRF computed with the proposed algorithm. It is obtained from a system with a negative cubic stiffness combined with a two-sided impact and the solution has up to five solutions at a certain frequency range. This result shows that even complex solution curves with sharp bends can be calculated with the algorithm.

12.4 Chaotic Motion

For the systems regarded in this contribution, it is not sufficient to limit simulations to periodic solutions to capture the overall dynamics. For these systems also aperiodic or chaotic motions can occur depending on the parameters. Therefore, the system is regarded in the time domain and it is transferred to the phase space leading to a system of differential equations of the form [4]

$$\displaystyle\begin{array}{rcl} \dot{x}_{1}& =& x_{2}, \\ \dot{x}_{2}& =& -f(x_{1},x_{2}) +\hat{ f}cos(x_{3}), \\ \dot{x}_{3}& =& \varOmega. {}\end{array}$$
(12.13)

Based on this system of first order differential equations the behavior of the system can be visualized in phase portraits and Poincaré-Maps. Phase portraits illustrate the relation of velocity, represented by x 2, and displacement, represented by x 1. This plot for instance provides information about the shape of limit cycles. It also gives a hint about the occurrence of chaotic motions. However, it is difficult to estimate the periodicity of a vibration based on phase portraits as the time is a parameter in these plots. To circumvent this drawback Poincaré-Maps are an useful addition. These plots are generated by regarding the trajectory in phase space stroboscopically at fixed intervals \(\Delta x_{3} = 1/\varOmega\). Hence, it is possible to directly conclude the periodicity based on the number of points in the Poincaré plot. In this context there are three relevant cases:

  • periodic solution with T = T exc : one point in Poincaré-Map

  • subharmonic solution with T = μ T Anr : μ points for the μ-th subharmonic

  • chaotic solution with T = ∞: infinite number of points, cumulated in certain areas

Poincaré-Maps as well as phase portraits are only valid for a specific parameter set with specific initial conditions. In order to make parameter studies, bifurcation diagrams are introduced to illustrate the behavior of a system over varying parameters or initial conditions. Therefore, the Poincaré-Maps are projected on one of their axes and plotted over one parameter.

To surely decide whether a system shows chaotic or periodic behavior the calculation of Lyapunov-Exponents is a popular method. The calculation of the Lyapunov-Exponents in this paper is based on the method of Wolf [10] where the Lyapunov-Exponents are defined as

$$\displaystyle{ \lambda _{n} =\lim \limits _{t\rightarrow \infty }\frac{1} {t}ln\frac{\left \vert \epsilon _{n}(t)\right \vert } {\left \vert \epsilon _{0n}\right \vert }. }$$
(12.14)

Geometrically, this means that the evolution of an infinitesimal n-sphere of initial conditions along a trajectory in phase space is regarded over time. Here, n is the dimension of the phase space and the Lyapunov-Exponents correspond to the evolution of the principal axes of the initial sphere. If the principal axes of the sphere shrink over time, all Lyapunov-Exponents are negative and all initial conditions within the sphere converge toward a limit cycle yielding a periodic motion. In contrast, if one of the axes grows over time the corresponding Lyapunov-Exponent is positive, which means that nearby initial conditions diverge. That implies that it is sufficient to regard the sign of the largest Lyapunov-Exponent to decide whether a system shows chaotic behavior or not. Thus, in the numeric examples only the result for the largest Lyapunov-Exponent is displayed even though the implemented method provides the whole Lyapunov spectrum.

12.5 Results

The first numeric example regarded in this paper is a SDOF-Oscillator with one-sided impact i.e. the cubic stiffness of the oscillator in Fig. 12.1 is set to β = 0. The remaining parameters of this example are listed in Table 12.1. Firstly, the FRF is calculated using the HBM with continuation. Therefore, the first four harmonics with \(\nu = \left \{1,2,3,4\right \}\) are taken into account as well as the subharmonic with ν = 1 and μ = 2. Due to the one-sided impact additionally the mean position of the vibration has to be regarded. Figure 12.3 displays the result obtained for the first four harmonics (left) as well as the mean position (right). It is obvious that there is a resonance frequency at about 0.3 Hz and several smaller peaks at lower frequencies appear which are caused by the higher harmonics. The mean position strongly depends on the amplitude as the high stiffness of the impact limits the penetration. In Fig. 12.4 the result for the second subharmonic is displayed, which smaller influence in the region of the resonance.

Table 12.1 Parameters for SDOF-Oscillator with one-sided impact
Full size table
Fig. 12.3
figure 3

Harmonics 1–4 (left) and mean position (right) for the SDOF-Oscillator with one-sided impact

Full size image
Fig. 12.4
figure 4

Subharmonic response for the SDOF-Oscillator with one-sided impact

Full size image

To examine the validity of the results, Fig. 12.5 (left) shows the displacement calculated with a time integration of the same system with sweep excitation. The results obtained with this method are alike regarding amplitude and resonance frequency. However, the result of the time integration additionally indicates the occurrence of chaotic behavior as the displacement varies strongly. This assumption can be confirmed by the calculation of Lyapunov-Exponents, of which the results are depicted in Fig. 12.5 (right) as well. These results also show that for the regarded system aperiodic motions appear, once the oscillator hits the impact. Exemplarily, Fig. 12.6 displays phase portraits and Poincaré-Sections for the vibrations at 0.15 Hz respectively 0.3 Hz. These visualizations show aperiodic motions which are dominated by the second harmonic at 0.15 Hz and the first harmonic at 0.3 Hz. As for the Poincaré-Sections the points are accumulated even though there is theoretically an infinite number of points.

Fig. 12.5
figure 5

Time integration results (left) and largest Lyapunov-Exponent (right) for the SDOF-Oscillator with one-sided impact

Full size image
Fig. 12.6
figure 6

Phase portrait and Poincaré-Map for the SDOF-Oscillator with one-sided impact at 0.15 Hz (left) and 0.3 Hz (right)

Full size image

In the following examples the focus is on combined nonlinearities, meaning that the cubic stiffness is now \(\beta \neq 0\). Nevertheless, the FRF can be calculated analogously to the ones in the previous example. First, a SDOF-Oscillator with positive cubic stiffness and the parameters listed in Table 12.2 is regarded.

Table 12.2 Parameters for SDOF-Oscillator with one-sided impact and positive cubic stiffness
Full size table

The corresponding FRFs calculated with the HBM under consideration of the harmonics \(\nu = \left \{1,2,3,4\right \}\) and the subharmonic with ν = 1 and μ = 2 is displayed in Fig. 12.7. The results show that multiple solutions occur in a frequency range of about 0.3–0.6 Hz. It is also interesting to observe that for the oscillator with cubic stiffness the harmonics with uneven numbers are dominant, but at the moment the impact is reached also harmonics with \(\nu = \left \{2,4\right \}\) start playing a role. The mean position is zero before the impact is reached due to the symmetry of the nonlinear force. When the oscillator impacts the mean position is shifted to negative values. The influence of the subharmonic response is according to Fig. 12.7 negligible. In comparison, the time integration in Fig. 12.8 (left) provides similar amplitudes but instead of the multiple solutions a jump in amplitude occurs.

Fig. 12.7
figure 7

Harmonics (left) and mean position (right) for the SDOF-Oscillator with one-sided impact and positive cubic stiffness

Full size image
Fig. 12.8
figure 8

Time integration results for the SDOF-Oscillator with one-sided impact and positive cubic stiffness (left) and negative cubic stiffness (right)

Full size image

The time integration also shows that for this example the solution is periodic in the regarded frequency range. Hence, the calculation of the Lyapunov-Exponents is dispensable. This also applies to the subsequently considered example for combined nonlinearities, which is a SDOF-Oscillator with negative cubic stiffness and the parameters listed in Table 12.3.

Table 12.3 Parameters for SDOF-Oscillator with one-sided impact and negative cubic stiffness
Full size table

In this example there are also multiple solutions at a certain frequency range, as the FRF for an oscillator with negative cubic stiffness is bent to the left. This effect is even stronger when the cubic nonlinearity is combined with an impact which can be observed in Fig. 12.9 for the harmonics with \(\nu = \left \{1,2,3,4\right \}\) (left). For the mean position of the vibration, shown in Fig. 12.9 (right), the same holds as for the previous example. However, an additional sharp bend occurs at the position where the oscillator detaches from the impact. This bend can be explained by looking at the subharmonic response for ν = 1 and μ = 2 which is displayed in Fig. 12.10. So, for this example the subharmonic response suddenly becomes dominant at the moment when the oscillator detaches from the impact, which causes additional solutions. In contrast, this cannot be observed in the time signals for the displacement with sweep excitation which is displayed in Fig. 12.8.

Fig. 12.9
figure 9

Harmonics (left) and mean position (right) for the SDOF-Oscillator with one-sided impact and negative cubic stiffness

Full size image
Fig. 12.10
figure 10

Subharmonic response for the SDOF-Oscillator with one-sided impact and negative cubic stiffness

Full size image

12.6 Conclusion and Future Work

This paper presented a method for the calculation of FRFs under consideration of sub- and higher harmonics. For the solution a Continuation Method based on tangent prediction and Gauss-Newton/Levenberg-Marquardt correction is adopted. With these methods it was possible to calculate FRFs with remarkable influence of sub- and higher harmonics as well as sharp bends in solution curves leading to multiple solutions in certain frequency ranges. The comparison of the FRFs with results obtained by time integration shows that the amplitude and mean position are approximated accurately. Even when the vibrations are actually aperiodic, which was shown by the Lyapunov-Exponents, it is possible to find a decent approximation of the resonance frequency, the amplitude and mean position of the vibration. For some systems it is also interesting that the presented method can also find unstable solutions which are difficult to obtain e.g. with time integration. Nevertheless, in some applications it is of interest to determine whether the vibration is periodic or aperiodic, which obviously is not possible by harmonic approximation. Therefore, calculations in the time domain and Lyapunov-Exponents can be beneficial. Consequently, it is often necessary to use a combination of different methods to capture the overall dynamics of a nonlinear system correctly.

For future research the concept for calculation of FRFs can be extended to systems with multiple degrees of freedom. In this context also the calculation of backbone curves to capture frequency-energy dependency of nonlinear systems is interesting. Additionally, the influence of the modeling of the impact has to be examined and validated experimentally.