Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

5.1 Introduction

Geophysical methods are applied to investigate the Earth’s interior. We obtain models of the Earth by imaging physical parameters such as density, electrical conductivity, or elastic properties using a variety of techniques. Here, we consider geophysical methods exploiting electric currents generated by electromagnetic (EM) induction or galvanic coupling to sense the electrical conductivity structure at depth. During the last years, these techniques have experienced rapid development for exploration purposes of the drillable subsurface. For instance, active controlled-source electromagnetic (CSEM) techniques are now frequently used together with seismic techniques to characterize resistive hydrocarbon reservoirs in offshore petroleum exploration. Deep saline aquifers exhibit high electrical conductivities and constitute one of the prime targets for electrical imaging methods, making these techniques one of the most important geophysical tools to characterize target horizons for \(\mathrm{{CO}}_{2}\) storage or geothermal reservoirs.

We attempt to enhance the reconstruction capabilities of geoelectric potential field and electromagnetic diffusion methods covering a wide range of scales from boreholes to regional and lithospheric dimensions. To reach these goals, we have developed an interdisciplinary concept integrating working groups from applied and numerical geophysics, information technology and numerical mathematics.

At first, we describe a joint inversion approach that uses data misfit and regularization in one objective function with different weights for each method. The implementation is based on the existing inversion framework ModEM by Egbert and Kelbert (2012) and Meqbel (2009) and incorporates CSEM, magnetotellurics (MT), and direct current (DC) (Spitzer 1995) finite difference (FD) forward operators. The parametrization is based on rectangular blocks. The second approach uses unstructured tetrahedral meshes for both the finite element forward (FE) operator and the parametrization. Rectangular grids are easy to construct and handle, but they are incapable of discretizing more complicated geometries such as steep surface topography or known subsurface structures like mining galleries. Keeping this in mind, we restrict ourselves here, however, to very simple geometries to make our results comparable.

A final section deals with a new method to parameterize the model in a more efficient way using wavelets. The idea behind is to compress the information describing coarse model structures by using a limited subset of wavelet coefficients. Inverting for these coefficients yields a less underdetermined problem and, thus, a potentially less biased solution.

5.2 Finite Difference Approach

In this section, we describe a joint inversion of the MT, CSEM and DC data using FD operators. The EM methods under consideration differ in their sensitivities towards resistive and conductive structures as well as in their exploration depths. While the MT method generally resolves conductive structures up to depths of the Earth’s upper mantle, CSEM and DC resistivity methods are sensitive to resistive layers in the uppermost crust. Thus, a proper weighting between different EM data sets is essential for a joint inversion. Here we present recently developed weighting schemes used for joint inversion of MT, CSEM and DC resistivity data. In addition, inverting multi-EM methods jointly requires the different forward modeling codes to be implemented in a common framework. For this purpose, we made use of the EM modular system ModEM of Egbert and Kelbert (2012) which uses the parallelization schemes described by Meqbel (2009). This package was initially developed to invert only MT data. For our joint inversion approach, we extended ModEM to include the forward modeling operators of CSEM using a secondary field formulation with a 1D analytic solution of Key (2009) and a DC resistivity solver by Spitzer (1995). All three solvers are capable of handling a three-dimensional distribution of electrical conductivity in the subsurface. Our proposed joint inversion scheme is based mainly on weighting the individual components of the total data gradient after each model update. Norms of each data residual are used to assess how much weight the individual components of the total data gradient must be given to result in a homogeneous contribution of all data sets to the inverse solution.

To demonstrate the efficiency of the proposed weighting schemes and to explore the contribution of each method we used synthetic data sets computed from a 3D synthetic model consisting of a shallow resistive thin block and a conductive and resistive larger block further below (Fig. 5.1a). These structures are embedded in a homogeneous background resistivity of \(10\,\Omega \mathrm{{m}}\). To demonstrate the resolution power of the MT and CSEM methods, we first inverted these two data sets separately. When fitting only the MT data, the inversion result in Fig. 5.1b shows that the conductive block is well resolved while the shallow and the deeper resistivity blocks are barely seen. In contrary, fitting the CSEM data separately results in a model in which the shallow thin resistive block is better resolved while only the tops of the deeper conductive and resistive blocks are imaged. As a next step, we inverted the MT and CSEM data jointly to test the new weighting scheme.

Fig. 5.1
figure 1

a Cross section (y-axis) through a 3D model used to compute the synthetic data. b and c show inversion results when fitting MT and CSEM data separately. d–e show joint 3D inversion results using the new weighting scheme d MT and CSEM, e CSEM and DC resistivity and f MT, CSEM and DC resistivity data. The inversion model in f resembles most closely the structures of the original model shown in a

Full size image

Figure 5.1d shows that combining MT and CSEM data and using an appropriate weighting results in a better image of the shallow thin resistive block as well as the deeper resistive and conductive blocks. The DC resistivity data are collected along three (synthetic) boreholes penetrating to a depth of about 700 m. Joint inversion of CSEM and DC resistivity data results in a more accurate reconstruction of the resistivity of the shallow thin block and a better definition of its lower and upper edges (Fig. 5.1e). In the last inversion experiment, we inverted all three data sets (MT, CSEM and DC resistivity) jointly. The model in Fig. 5.1f clearly demonstrates that joint 3D inversion is feasible. More importantly it shows, that a combination of these three methods results in a much better image of the subsurface than what can be achieved with any of the individual methods.

Fig. 5.2
figure 2

Vertical section extracted from the 3D inversion model along the receiver line. Lines and triangles indicate transmitters and receivers, respectively. The star shows the position of the \(\mathrm{{CO}}_{2}\) injection well

Full size image

An additional thread of our developments on the basis of FD involves a fully distributed parallel three-dimensional CSEM inversion algorithm (Grayver et al. 2013). Ideas presented in Streich (2009) were further elaborated and incorporated into this new code. The inversion algorithm is based on Gauss-Newton minimization and uses a parallel distributed direct-solver for FD forward modeling. The forward modeling implements efficient routines to handle realistic source geometries accurately (Streich and Becken 2011). This inversion scheme has been used to invert real CSEM data collected across the Ketzin \(\mathrm{{CO}}_{2}\) storage formation, 15 km west of Berlin (Grayver 2013). Figure 5.2 shows resistivities obtained from the 3D inversion along the receiver line. The image contains several prominent conductive and resistive horizontally continuous structures that also appeared nearly identically for different inversion setups. The regional geology is well constrained, with an anticline structure of sediments overlying a salt pillow ( Förster et al. 2009). The top of the anticline is at a depth of approximately 2 km near the center of our survey line. The electrical conductivity structures recovered by 3D CSEM inversion correlate well with the main geological units (Klapperer et al. 2011).

5.3 Finite Element Approach

The joint inversion schemes introduced above are based on classical FD forward operators using structured grids, which are limited with respect to discretizing complex structures such as topography, bathymetry or generally curved objects. As a part of Multi-EM we have therefore developed 3D forward modeling and inversion schemes based on FE on unstructured tetrahedral grids. These approaches allow for an easy incorporation of complicated, more realistic model geometries, which are encountered in the geosciences. A further major difference to the inversion concept described above is the sequential mode of cycling through the individual inversion of each EM method using the output of the previous scheme as the reference model for the following one. In this way, we do not have to determine the full set of regularization parameters all at once which is a major difficulty due to their inherent uncertainty. In order to achieve a solid and unified software base for our FE methods, we have implemented all new forward and inverse operators in MATLAB. The resulting code is modularized and the interfaces between model geometry, grid generator and inverse operator are being standardized so that the individual EM method may conveniently access the model and pass the inversion output over to the subsequent program. The EM methods we are reporting on are DC and TEM. However, FE solutions for CSEM and MT (Franke-Börner et al. 2012) are near completion ultimately providing the capability of joint inversion of all four EM methods.

The DC resistivity code by Weißflog et al. (2012) enables us to model complex topography and to extract the derivatives, which are crucial for the inversion while retaining full control over the assembly process of the system matrix. For simplicity, we apply a regularized Gauss-Newton method. To stabilize the inversion procedure and provide additional information to avoid ambiguities, a suitable regularization strategy is necessary. As our inversion approach is based on a FE discretization of the equation of continuity using a piecewise constant representation of the conductivity model, a regularization operator is required that is applicable to piecewise constant model parameters on unstructured grids. We have therefore implemented a smoothness regularization by (Schwarzbach and Haber 2013) in which the penalty function measures the norm of a weak gradient of the conductivity field. The latter is evaluated using duality techniques with H(div)-conforming Raviart-Thomas vector elements of lowest order.

For solving the 3D transient electromagnetic (TEM) problem we have developed two different approaches. Both use Nédélec finite elements to discretize the spatial part of the curl-curl equation for the electric field. In the first method, the time evolution of electromagnetic fields is propagated forward in time, whereas in the latter the Fourier components of these fields are computed for a suitable set of frequencies, which are then transformed numerically into the time domain. Each of these methods is numerically challenging if not, as in the case of explicit time stepping, prohibitively expensive. We have therefore employed rational Krylov subspace techniques (RKST) to reduce the numerical costs both in the time and the frequency domain. In the time domain, RKST are used in conjunction with a geometric multigrid method to solve the resulting linear system of ordinary differential equations. In this way, the initial electric field is advanced to only a small set of selected times of interest (Afanasjew et al. 2013). In the frequency domain, RKST are applied as a model reduction technique where the resulting system matrix is projected onto a low-dimensional subspace retaining the information of the main eigenvalues (Börner et al. 2013).

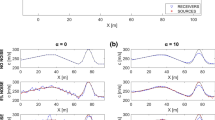
In the following experiments we limit ourselves to two dimensions. However, the methodology applies to 3D scenarios in the same manner. To demonstrate the advantage of a joint TEM/DC approach and showcase the respective properties of the different methods, the model (Fig. 5.3a) consists of two smaller bodies of high conductivity close to the surface and a larger structure of high resistivity buried at greater depth within a \(100\,\Omega \mathrm{{m}}\) background. First, the synthetic data for TEM and DC were independently calculated on different grids. Then the inversion process was started for TEM and DC using a homogeneous reference model on a common inversion mesh (i.e., parametrization) resulting in inverse models displayed in Fig. 5.3b, c, respectively. It is easy to see that the TEM configuration (with receivers located between \(-200\) m and \(+200\) m and two sources on the surface) is not able to resolve the deeper structure while being able to distinguish the two shallow bodies quite clearly. Our DC setup is a pole-pole configuration with four sources on the Earth’s surface and one borehole source at a depth of 350 m. The receivers are located along the surface between \(\pm 600\,\mathrm{{m}}\). The DC inversion reconstructs the large structure at depth while failing to separate the smaller objects to our satisfaction. Figure 5.3d shows the DC inversion result using the same configuration as described above and the TEM solution (Fig. 5.3b) as the reference model. Combining the individual resolution properties of these two methods yields a better image of the two conductive blocks as well as of the resistive body at greater depth.

Fig. 5.3
figure 3

a The true model used to compute the synthetic data. b and c are the inversion results for only TEM and DC data, respectively. d Using the TEM solution as the reference model, we then inverted the DC resistivity data to obtain a joint inversion result, which recovers the three anomalous bodies well

Full size image

5.4 Sparse Inversion in Wavelet Domain

The preceding inversion examples relied on a parametrization of the subsurface into disjoint blocks of piecewise constant resistivity. In such bases, complex structures are most conveniently represented by using a large number of small model blocks to allow for the needed degree of detail and flexibility to describe the resistivity distribution. This approach introduces a large solution null-space, and the commonly applied smoothing regularization techniques result in heavily biased model estimates.

Here, we investigate alternative bases to represent resistivity that allow for a sparse representation of the resistivity distribution. The term sparse is used here to indicate that the model is described with as little as possible non-zero coefficients. Sparse image recovery has in the last years become a rapidly developing field in compressed sensing, and has proven particularly successful in medical imaging. Here, we apply these concepts for the first time to electromagnetic geophysical imaging problems by transforming the resistivity image into wavelet domain and estimating the significant wavelet coefficients.

A wavelet multi-resolution basis admits the approximation of a function with different levels of details on various scales. Because many of the details contained in images are unimportant, the corresponding coefficients can be threshold from the decomposition in order to obtain a compressed version of the original image. We attempt to exploit these compression capabilities of wavelets in the framework of the inverse magnetotelluric problem. We formulate the following objective: determine the few non-zero wavelet coefficients which are required to represent a model that can explain the observed data. Accordingly, the approach falls into the class of sparsity-constrained inversion schemes. These schemes minimize the combination of the data misfit in a least squares (L2) sense and of a model coefficient norm in a L1 sense (L1-L2 minimization). The minimal L1 coefficient norm renders the solution sparse, in contrast to an L2 norm minimization that renders the solution smooth (cf. Fig. 5.4a).

Fig. 5.4
figure 4

Sparse Inversion. a Solution simplicity, expressed in the L2 and L1 norms of model parameters for a simple two-parameter problem. Among all possible solutions (solid line), the objective of minimal L1 norm yields a sparse solution (open dot, with \(\mathrm{{m}}_{1} = 0\)), whereas the minimal L2 norm is found for a smooth solution with \(\mathrm{{m}}_{1} \approx \mathrm{{m}}_{2}\). Figure modified after Loris et al. (2007). b Inversion examples for a two-blob model. True model (upper panel) used to generate synthetic data and db4 (middle panel) and bior2.2 (lower panel) inversion models that fit the data to within their randomly generated errors. Both inversion models require only a fraction of non-zero coefficients when compared to standard block parametrizations

Full size image

The minimization of a L1-L2 objective is problematic, because the function is non-convex and non-differentiable. We applied a primal-dual-interior point method which has shown to be efficient for L1-L2-norm minimization (Borsic and Adler 2012). The algorithm inverts for a differentiable approximation of the L1-norm. The formulation seeks to minimize the gap between a primal and a dual objective function and is iteratively solved for with a Newton method.

The appearance of sparse wavelet models is dependent on the particular choice of wavelets. We have focused on smooth wavelets that result in smooth resistivity models, similar to those generated with the notably different smoothing regularized inversion scheme. However, only a fraction of coefficients is required to represent the model. Figure 5.4b depicts, as an example, inversion models estimated from synthetically generated, noise-contaminated data using a five-level db4 (middle panel) and bior2.2 wavelet representation (lower panel). The true model used to generate the data is depicted in the upper panel. We find that about 60 wavelet coefficients are sufficient to describe a model that fits the data.

For the example in the Fig. 5.4, the forward solutions were obtained with a FE approach (Lee et al. 2009) that solves the induction problem for the uncompressed resistivity distribution reconstructed from the wavelet representation. Rectangular elements were employed. The wavelet sensitivities were evaluated by projecting the space domain sensitivities into wavelet domain.

Our results demonstrate that over-parametrization of the model region can be eliminated by projecting the model domain into a sparsifying basis. This proposed approach results in an alternative class of models by invoking sparsity based regularization; it may furthermore yield computational benefits provided that sparsity could be exploited in the evaluation of the Jacobian. Our approach could also be beneficial for model appraisal when evaluating resolution and covariances for a limited set of coefficients.

5.5 Conclusions

This project has given us the possibility to explore various strategies of joining different EM methods in common inversion schemes. The outcome is clear: combining two or more EM techniques in a complementary way may enhance the ability to reconstruct subsurface conductivity structures. However, the way to achieve this aim is multifaceted. The existing inversion framework ModEM offers a practical environment to rapidly incorporate existing forward modeling software. With respect to the inversion strategy the main problem is the determination of a set of regularization parameters all at the same time. We have therefore begun to investigate a sequential mode where the inversion result of one method serves as a reference model for the next. Using synthetic models, both approaches have demonstrated that the combination of EM methods may produce enhanced images of the subsurface compared to individual inversions.

Moreover, we have learned in the course of the project that mixing FD and FE approaches is unrewarding because the strengths of each approach are diminished. Whereas the FD method takes advantage of its simplicity, the sparsity of the resulting system matrix and the relatively small efforts of administering rectangular Cartesian grids, the FE method stands out due to its enormous flexibility with respect to adapting any given geometry using unstructured meshes. At first glance, FD might be the method of choice if it comes to inversion because the structures to be reconstructed are initially not known and, thus, grid adaptivity does not play an important role. However, given topography, subsurface structures as caves or voids, and a-priori information from, e.g., seismics may put high requirements on the future inversion software. The price to pay is the increased administrational effort for FE.

We have also acquired first experiences with alternative model parametrization techniques in the wavelet domain. We apply for the first time compressed sensing concepts to the inversion of magnetotelluric data and recover a sparse solution by minimizing a mixed L1-L2 norm objective function.

Finally, we have extensively used massively distributed computations for 3D inversions. In fact, working with real-world problems and in general with large model domains and comprehensive data sets requires adequate computer hardware that continuously offers an increasing number of computing cores, at least for the foreseeable, middle-term future. High-performance computing on a moderate or large number of nodes goes therefore hand in hand with innovative mathematical and numerical concepts. Thus, this project marks a starting point for a wide variety of further research efforts in EM inversion based on the research results at hand.