Keywords

1 Introduction

Image interpretation and processing is a fundamental analysis in most of medical applications [5]. The main objective is to help the analyst in the interpretation of the results while introducing quantitative data. In some cases, the attention is focused on surface detection, while in other contexts, the observation is dedicated to morphological changes or surface extension (strain or deformations).

Considering rigid body detection and surface out of plane measurements, this item has been extensively studied by many researchers [11]. In many cases the objective is directed towards the recognition of objects, whatever is their spatial positioning and minimal surface deformation. This is often accomplished by methods that make use of patterns of key points [9].

For the reconstruction of surface deformations many efforts have been done by researchers, in both 2D and 3D approach, some of these methods have been compared in [14]. The general achievements show that many benefits are gained if the entire acquired image is simultaneously considered; this is to say non-considering each subset individually. In this optics, some smoothing can be achieved by B-spline regularization [3] or by finite element formulation for the acquisition of the deformation field [7] by DIC.

In the present chapter the attention is firstly devoted on the capability to extract the geometric shapes of a surface, originally flat. This means that the interest is not only directed towards object recognition, but to new surface characteristics for the identification of its off-plane displacements. In the present case the tests consider the displacement of a sheet of paper, easily deformed in the out of plane orientation but experiencing minor surface strains. Within the paper, it is demonstrated that using an effective image, sufficiently variegated (such as a speckle image or any other non-uniform and non-periodical picture) is equivalent to a regularly meshed grid [1]. This equivalence is achieved by mapping the picture through a regular or non-regular mesh of quadrilateral sub-images (elements). These non-superimposed sub-images are managed as four node bilinear membrane elements, well known in finite element analysis. Each element of the grid maintains its peculiarity because it is characterized by a different color content and distribution (sub-image).

Another aspect, that makes use of the same image recognition methods, regards the capability to extrapolate the strains experienced by mating surfaces using non-invasive methods. The most promising methods involve photographic techniques, such as digital image correlation [4, 12–14]. Usually the strain and motion analysis procedures make use of a sequence of pictures that follows the whole strain progress [2]. In this chapter a method that requires only two images is proposed; the first is taken when no loads are applied, the second one when all loads and resulting deformations are settled. This method can thus be applied in principle when a limited number of images are available, as the initial and the final image only.

There exist 2-D digital Correlation techniques as well as 3-D ones [10]. Here we deal with 2-D technique which is based on the use of a single camera. Most of the techniques are based on sub-image correlations. This means that the local correlation imposed on a sub-image does not have an influence on all other correlations performed on sub-images far away from the previous one. In this chapter, according to former approaches [1, 3], we discuss a technique that solves the displacement fields as a whole, so that the continuity conditions is fulfilled in the whole processed image.

When consistent displacements are faced, the correlation techniques meet considerable difficulties to keep precision, as discussed in [12].

The displacement field solution generally needs the handling of a very high number of equations; this can even attain the order of the number of pixels recorded into the image. Therefore, a technique directed to reduce the number of equations while increasing the efficiency is discussed.

2 Out of Plane Surface Deformation

The geometric model adopted is the simple equivalent pinhole camera. According to this assumption, being f the distance between the pinhole and the image sensor, the following ratios can be written:

$$\begin{aligned} {X}' = -\frac{f}{Z}X; \qquad {Y}' = --\frac{f}{Z}Y; \qquad {Z}'=-f \end{aligned}$$
(1)

The negative sign is generally changed by considering the image projected between the viewing point and the object (Fig. 1).

In the pinhole assumption, the complex dioptric lens system is substituted by an ideal single lens, infinitesimally thin, thus the optical system agrees with the following assumptions [15]:

  • all parallel light rays are concentrated on the focus;

  • no refraction is induced to all rays passing through the lens center;

  • all non-centered rays are deviated in correspondence of the middle plane.

Other assumed hypotheses, adopted when dealing with digital images are:

  • the optical axis is perfectly orthogonal to the sensor plane and centered on it;

  • the sensor gauge is organized by a two perfectly orthogonal cell disposition.

Fig. 1
figure 1

Scheme of pinhole camera view

Full size image

2.1 Identification of Grid Images

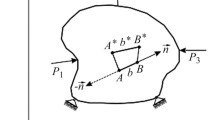
In this section we assume that the image is simply constituted by a regular square grid. In the next section the association of a grid to a general image is discussed. Figure 2 shows the projection of a simple square on the CCD plane that is reversed, as usually. The geometry projected on the plane is given by the four vectors connecting the observation point to the square corners.

Once the image is digitally acquired, each vector v associated to a point is known in its direction, while its magnitude remains unknown. All unknowns are represented by the moduli associated to the respective vectors. According to this logic, all vectors U are computed as differences of vectors V (Fig. 2). In the following, the vectors V will be addressed making use of respective unit vectors: \(\mathbf{V} = \mathrm{m} \cdot \mathbf{v}\).

Fig. 2
figure 2

Vectors identifying the positioning of element nodes

Full size image
Fig. 3
figure 3

Nomenclature of a \(3\times 3\) grid

Full size image

Making reference to the \(3\times 3\) grid represented in Fig. 3, the first element gives the following equations:

$$\begin{aligned} \begin{array}{l} \mathbf{U}_\mathbf{1} =\mathbf{V}_\mathbf{5} \mathbf{-V}_\mathbf{1} =m_5 \mathbf{v}_5 -m_1 \mathbf{v}_1 \\ \mathbf{U}_2 =\mathbf{V}_6 \mathbf{-V}_5 =m_6 \mathbf{v}_6 -m_5 \mathbf{v}_5 \\ \mathbf{U}_3 =\mathbf{V}_2 \mathbf{-V}_\mathbf{1} =m_2 \mathbf{v}_2 -m_1 \mathbf{v}_1 \\ \mathbf{U}_4 =\mathbf{V}_6 \mathbf{-V}_2 =m_6 \mathbf{v}_6 -m_2 \mathbf{v}_2 \\ \end{array} \end{aligned}$$
(2)

Being the grid formed by equal squares, several conditions can be imposed to each of them - note that not all of them are independent - represented in Table 1.

Table 1 Vector and scalar conditions for a square grid
Full size table

The equations given in the previous Table 1 generates, using the modules as the unknowns, the following 14 equations (first two are vector equations):

$$\begin{aligned} \begin{array}{l} m_1 m_5 \left( {\mathbf{v}_5 \times \mathbf{v}_1 } \right) -m_1 m_6 \left( {\mathbf{v}_6 \times \mathbf{v}_1 } \right) -m_2 m_5 \left( {\mathbf{v}_5 \times \mathbf{v}_2 } \right) -m_2 m_6 \left( {\mathbf{v}_6 \times \mathbf{v}_2 } \right) =\mathbf{0} \\ m_1 m_2 \left( {\mathbf{v}_1 \times \mathbf{v}_2 } \right) -m_1 m_6 \left( {\mathbf{v}_1 \times \mathbf{v}_6 } \right) -m_2 m_5 \left( {\mathbf{v}_5 \times \mathbf{v}_2 } \right) +m_5 m_6 \left( {\mathbf{v}_5 \times \mathbf{v}_6 } \right) =\mathbf{0} \\ \end{array} \end{aligned}$$
(3)
$$\begin{aligned} \begin{array}{l} m_1 m_5 \left( {\mathbf{v}_1 \cdot \mathbf{v}_2 } \right) -m_1 m_6 \left( {\mathbf{v}_1 \cdot \mathbf{v}_6 } \right) -m_5 m_5 \left( {\mathbf{v}_5 \cdot \mathbf{v}_5 } \right) +m_5 m_6 \left( {\mathbf{v}_5 \cdot \mathbf{v}_6 } \right) =0 \\ -m_2 m_6 \left( {\mathbf{v}_2 \cdot \mathbf{v}_6 } \right) +m_2 m_5 \left( {\mathbf{v}_2 \cdot \mathbf{v}_5 } \right) -m_5 m_6 \left( {\mathbf{v}_5 \cdot \mathbf{v}_6 } \right) +m_6 m_6 \left( {\mathbf{v}_6 \cdot \mathbf{v}_6 } \right) =0 \\ m_1 m_2 \left( {\mathbf{v}_1 \cdot \mathbf{v}_2 } \right) -m_1 m_6 \left( {\mathbf{v}_1 \cdot \mathbf{v}_6 } \right) -m_2 m_2 \left( {\mathbf{v}_2 \cdot \mathbf{v}_2 } \right) +m_2 m_6 \left( {\mathbf{v}_2 \cdot \mathbf{v}_6 } \right) =0 \\ m_1 m_1 \left( {\mathbf{v}_1 \cdot \mathbf{v}_1 } \right) -m_1 m_2 \left( {\mathbf{v}_1 \cdot \mathbf{v}_2 } \right) -m_1 m_5 \left( {\mathbf{v}_1 \cdot \mathbf{v}_5 } \right) +m_2 m_5 \left( {\mathbf{v}_2 \cdot \mathbf{v}_5 } \right) =0 \\ \end{array} \end{aligned}$$
(4)
$$\begin{aligned} \begin{array}{l} m_1^2 \sum \limits _{i=1}^3 {\nu _{1\left( i \right) }^2 } -2m_1 m_3 \sum \limits _{i=1}^3 {\left( {\nu _{1(i)} \nu _{5(i)} } \right) ^{2}+m_5^2 \sum \limits _{i=1}^3 {\nu _{5\left( i \right) }^2 } } =L^{2} \\ m_5^2 \sum \limits _{i=1}^3 {\nu _{5\left( i \right) }^2 } -2m_5 m_6 \sum \limits _{i=1}^3 {\left( {\nu _{5(i)} \nu _{6(i)} } \right) ^{2}+m_6^2 \sum \limits _{i=1}^3 {\nu _{6\left( i \right) }^2 } } =L^{2} \\ m_2^2 \sum \limits _{i=1}^3 {\nu _{2\left( i \right) }^2 } -2m_2 m_1 \sum \limits _{i=1}^3 {\left( {\nu _{2(i)} \nu _{1(i)} } \right) ^{2}+m_1^2 \sum \limits _{i=1}^3 {\nu _{1\left( i \right) }^2 } } =L^{2} \\ m_6^2 \sum \limits _{i=1}^3 {\nu _{6\left( i \right) }^2 } -2m_6 m_2 \sum \limits _{i=1}^3 {\left( {\nu _{6(i)} \nu _{2(i)} } \right) ^{2}+m_2^2 \sum \limits _{i=1}^3 {\nu _{2\left( i \right) }^2 } } =L^{2} \\ \end{array} \end{aligned}$$
(5)

All above equations give a non-linear (quadratic) system of equations where the unknowns are vector magnitudes. If one considers all possible combinations of products of unknowns as unknowns themselves, they turn to be 10 for a single element, with 14 equations each. As an example, for the element n. 1 of Fig. 3, the 10 unknowns are listed in Table 2.

Table 2 List of unknowns produced by a single element
Full size table

The full system of equations is therefore over-determined and the solution can be found solving all the quadratic unknowns involved. After the full solution, each vector magnitude is computed by the root square of the quadratic unknowns. Furthermore, the mixed product of the unknowns can be used to check the accuracy of the solution gained.

2.2 Virtual Image Embedded on a Picture

If an image is present on a surface, this can be associated to a virtual grid. The point is to guarantee that the grid follows the changes of the image, due to movements of the surface that can be considered as a combination of rigid and deformable displacements.

This can be accomplished by considering the grid as a mesh of bilinear finite elements, whose movements guarantee the continuity of the surface. Each element contains a part of the initially flat image; this information is maintained in a natural coordinate system as shown in Fig. 4.

Fig. 4
figure 4

Physical/Natural coordinate systems

Full size image

Such reference approach is particularly suitable to compare elements that are initially irregular or become irregular due to large displacements on the image. Therefore, each sub-image is interpolated though a cubic spline approach. By this procedure, each element is always square-represented and keeps the same image content. In Fig. 5 is shown an example of how interpolation deforms the image.

Fig. 5
figure 5

Change from physical to natural coordinates

Full size image

2.3 Results on Out of Plane Deformation

The data here presented, apart the very next subsection, refers to all effective pictures taken with a focal distance equal to 29 mm, corresponding to a printed paper positioned at 1500 mm from the ideal lens center. All images have been obtained with an aperture equal to 1/8 to increase overall focus depth.

2.3.1 Test of the Procedure on Exact Grids

The theoretical correctness of the procedure presented has first of all been investigated through the application on a simulated grid (no pictures does effectively exist) that has been deformed applying one or two finite curvatures. We can see that the reconstruction is perfectly accurate (no digital error on pixel definitions is present since pixel positions are recorded with 12 digit precision) only if the local orientation of the grid causes a single curvature change \((R_{c} = 1430\,\mathrm {mm})\). It is interesting to highlight that the application of a small noise (1 % of the diagonal length of a single element) reduces considerably the precision if the results are very accurate, but does not appreciably changes the behavior if discrepancies are already encountered when data are not affected by noise.

From the above reasons, it is clear that the assumption of square grid to maintain its shape is very strong, difficult to obtain when double curvature are present. This means that the size of the elements of the grid should be taken as small as the curvature increases. As a matter of fact, the last row in Table 3 shows much better results in this case, as expected (double curvature keeping the same equivalent value than single curvature case).

Table 3 Noise effect on accuracy for various curvatures
Full size table

2.3.2 Tests on Pictures of Printed Grids

The grid is printed on a sheet of paper that is first photographed in a plane orthogonal to the focal axis, and the second picture considers the sheet deformed in various ways, such as the one shown in Fig. 6.

Four cases are here presented; (i) it concerns a \(5-10-15^{\circ }\) rigid rotation of the paper on a vertical axis as to generate a prospective view; (ii) it regards a simple half-fold oriented as the vertical axis in the center, and folded at a corner; (iii) the paper leaned on a cylinder (diameter = 450 mm) with a vertical axis; (iv) the paper applied on the same cylinder with the sheet base inclined of \(30^{\circ }\).

Fig. 6
figure 6

Digital pictures of the printed grid, a before and b after off-plane deformation

Full size image

In Fig. 7 two operating ways are compared: the black lines show the results when the over-determined solution is performed on all squares at the same time, the blue lines consider the solution performed at each square, individually. The whole solution is much better than the second, since pixel errors compensate.

Fig. 7
figure 7

Comparison of overall result and square dispersion for; a printed grid, b virtual grid on speckle image

Full size image

Table 4 shows the errors introduced when varying sheet inclination.

The results show that a rigid displacement on one of the grid axes can be managed by the method in the average by both images (grid or speckle above discussed) (Fig. 8).

The two cases of folds considered (ii) reveal a particular behavior of the algorithm. As a matter of fact, the mean square method tends to compensate the errors so that there is the tendency to keep flat in one direction. Referring to Fig. 9a and b the dispersion is illustrated when the fold is located in the center or in the corner, respectively. The maximum determined fold displacement respects the values imposed in the test within a 2 % error. Figure 10b results seem to be erroneously similar to the previous case, as the top views show. It is clear that the identification algorithm is affected by eventual curvatures non-aligned with the grid. In practice, since the algorithm tends to maintain the overall length at each element, it encounters some difficulties while managing elements that change all side-length due to curvatures imposed.

Table 4 Angle identified when varying the point of view
Full size table
Fig. 8
figure 8

Top view of the profiles for case (ii): a vertical fold b corner fold, c vertical fold for speckle image

Full size image
Fig. 9
figure 9

Dispersion of individually identified elements for: a vertical cylinder, b inclined cylinder

Full size image

The results performed on cylindrical surfaces confirm the deficiencies previously indicated on double curvature grids. As a matter of fact the comparison between cases (a) and (b) in Fig. 9 shows a much more evident dispersion of single computed squares (blue) when the sheet base is inclined toward horizon—relative full picture is visible in Fig. 7b. The global results (black lines) of case (a) are quite accurate (error in radius lower than 1 %) while case (b) provides erroneous results.

2.3.3 Tests on a Printed Speckle Picture

Indeed, the application of a virtual grid introduces some additional errors by respect to the printed grid. These errors amplify the deficiencies already evidenced before. The algorithm used to detect the displacement of the virtual grid by means of speckle deformed image is presented in the next session. The convergence is achieved by means of minimum square error search. For example, one can compare the results given in Figs. 10 and 11a and b, respectively. Case (a) identifies the virtual grid imposed on the image to be taken as reference; case (b) in Fig. 10 shows good identification that can also be seen in Fig. 7b through square dispersion. On the contrary, one can see that the corner correspondence on Fig. 11a, b is very poor, particularly at the left top corner where the deformations are the highest, according to results presented in Fig. 9b.

Fig. 10
figure 10

Virtual node locations before and after \(5^{\circ }\) inclination

Full size image
Fig. 11
figure 11

Virtual node locations before and after application on inclined cylinder

Full size image

2.3.4 Discussion on Out of Plane Deformations

It is evident that algorithm proposed here shows some difficulties when applied to structures that deforms with effective double curvatures. As a matter of fact, when double curvatures are present, the side lengths cannot be computed accurately by simple node distances. A better computation should accounts of effective surface distance through an iterative procedure that takes into account of geometry on curved surfaces. From another point of view, the advantage of the method is that no regularization conditions are required to the identifying surface, so that no simplified shape is accounted for the surface out of plane deformation. An idea of the solution accuracy can be reached from the dispersion of the results when computation regards each square element individually. When the dispersion is high the global results is correspondently worse. Use of speckle image instead of a printed grid is possible and a theoretical increment of information is available. However, the differential method, discussed hereinafter, requires a limitation of the displacements introduced in the image to keep consistency. When the strain are less than 50 % of the virtual grid nodes moves correctly, for higher values accuracy problems become evident.

3 Differential Method

The deformation field is calculated by comparing the original image and the deformed one. In this work a global approach is followed [2]. The problem consists in the minimization of the error functional defined by the following formula:

$$\begin{aligned} \hbox {E }= \sqrt{\sum _{\text {i}} {\left[ {I_d (x_i ,y_i )-I_u (x_i ,y_i )} \right] ^{2}} } \end{aligned}$$
(6)

where \(I_{u} I_{d }\) represent the images before and after deformation. \(x_{i}, y_{i}\) are the i-th pixel coordinates into the images. The summation comprehends all pixels. To each element a sub-image is associated. At each sub-image (corresponding to a single finite element) the internal spatial distribution is based on the displacements of the four nodes bordering the element. The solution allows finding the node locations that make it possible to overlap the undeformed image onto the deformed one. Once the image is divided into sub-images, it is possible to write the formula (6):

$$\begin{aligned} \mathbf{E} = \sqrt{\sum _{\text {j}} {\left\| {\mathbf{S}_j (\mathbf{x})-\mathbf{S}_{j0} (\mathbf{x}_0 )} \right\| ^{2}} } \end{aligned}$$
(7)

where \(\mathbf{S}_{j}, \mathbf{S}_{j0}\) are the j-th sub-image, while x and \(\mathbf{x}_{0}\) represent the final and initial nodal coordinates, respectively. The rate of change between x and \(\mathbf{x}_{0}\) is non-linear; for this reason it is not possible to directly find the solution, but an iterative procedure is needed. The algorithm consists in the linearization of the non-linear least squares problem. It is based on Taylor series expansion, truncated to its first order, of the sub-image when varying the generic nodal coordinate:

$$\begin{aligned} \mathbf{S}_j (X^{\prime }) = \mathbf{S}_0 (X_0 )+\sum _{\text {k}} {\frac{\partial \mathbf{S}_{\text {0}} }{\partial \text {x}_{\text {k}} }(x_k -x_{k0} )} \end{aligned}$$
(8)

For the sake of clarity, the same is written in matrix formulation, evidencing the Jacobian matrix:

$$\begin{aligned} \left[ {{\begin{array}{cccc} {\frac{{\partial \mathbf{S}}_{1,0}}{\partial \hbox {x}_{1}} }&{} {\frac{\partial \mathbf{S}_{1,0} }{\partial \hbox {x}_{2} }}&{} \cdots &{} {\frac{\partial \mathbf{S}_{1,0} }{\partial \hbox {x}_{M} }} \\ {\frac{\partial \mathbf{S}_{2,0}}{\partial \hbox {x}_{1} }}&{} {\frac{\partial \mathbf{S}_{2,0} }{\partial \hbox {x}_{2} }}&{} \cdots &{} {\frac{\partial \mathbf{S}_{2,0} }{\partial \hbox {x}_{M} }} \\ \vdots &{} \vdots &{} \cdots &{} \vdots \\ {\frac{\partial \mathbf{S}_{\text {N,0}} }{\partial \hbox {x}_{1} }}&{} {\frac{\partial \mathbf{S}_{\text {N,0}} }{\partial \hbox {x}_{2} }}&{} \cdots &{} {\frac{\partial \mathbf{S}_{\text {N,0}} }{\partial \hbox {x}_{\text {M}} }} \\ \end{array}}} \right] \cdot \left\{ {{\begin{array}{c} {x_1 -x_1 ^{\prime }} \\ {x_2 -x_2 ^{\prime }} \\ \vdots \\ {x_M -x_M ^{\prime }} \\ \end{array}}} \right\} = \left\{ {{\begin{array}{c} {\mathbf{S}_{1,0} -{\mathbf{S}_{1,j}}^{\prime }} \\ {\mathbf{S}_{2,0} -{\mathbf{S}_{2,j} }^{\prime }} \\ \vdots \\ {\mathbf{S}_{N,0} -{\mathbf{S}_{N,j}}^{\prime }} \\ \end{array} }} \right\} \end{aligned}$$
(9)

or the equivalent \(\mathbf{J}\cdot \Delta \mathbf{x}=\Delta \mathbf{s}\). Each term of the Jacobian matrix is composed by a number of elements that coincides with the number of pixels contained in the sub-image. Therefore, the matrix shows considerable dimensions. The computation is based on centered first derivate, evaluated by considering the pixels around each node. For this reason, the Jacobian matrix of the reference image is computed by respect to all possible node displacements. As mentioned before, the Jacobian matrix is composed of partial derivatives. Each matrix derivative is calculated by the four central point derivatives by respect to the unknowns as:

$$\begin{aligned} \frac{\partial \mathbf{F}(x)}{\partial x}=\frac{1}{12h}\left[ {\mathbf{F}(x-2h)-8\mathbf{F}(x-h)+8\mathbf{F}(x+h)-\mathbf{F}(x+8h)} \right] \end{aligned}$$
(10)

where h denotes the discretization step. For example, the term F (x-2h) represents the sub-image when a node is moved back 2h. The choice of the parameter h is crucial. The solution requires the minimization of the error (7) through an iterative procedure. As a matter of fact the inversion of the Jacobian matrix is required (9):

$$\begin{aligned} \Delta \mathbf{x}=\mathbf{J}^{-1}\cdot \Delta \mathbf{s} \end{aligned}$$
(11)

The Jacobian matrix is a sensitivity matrix; however, its costly inversion must be performed just once. When the displacements of all nodes have been computed, it is easy to gain the internal strains, known by means of the nodal displacements of each element. This is made possible through the pre-multiplication of the vector of element nodal displacements by the matrix B (obtain by appropriate derivative of Q4 shape functions) [16] if first order approximation is accepted, or more sophisticated expressions if first order simplification is not applicable.

3.1 Convergence Enhancement

In this section, the optimal choice of the number of internal points, to achieve a quick convergence of the results, is discussed. A criterion to reduce the equations and to speed-up the solution process is introduced. As an example, for a high-definition \(3000\times 4000\) pixel image, meshed through almost 10000 elements having eight degrees of freedom each, a 240 billion of equations results. In this chapter two possible techniques have been developed; the first considers possible grouping of pixels belonging to confined areas, the second one makes use of Hu’s invariants to discriminate each sub-image.

3.1.1 Method I: Grouping Technique

The technique of grouping is helpful to reduce the number of equations to solve. As cited before, the Jacobian presents a considerable dimension; in fact each term of the matrix is a partial derivative of the sub-image. The grouping method introduced in this chapter, handles the single partial derivative of the sub-image. These are divided into sub-areas, and a sum of the values inside them is considered, as shown in Fig. 12.

Fig. 12
figure 12

Grouping technique representation

Full size image

By this way, the number of equations is reduced, and the iterative calculation speeds up. The size of the grouping is important, and must be wisely chosen. A considerable grouping amount is required for saving computational time, the data information, is reduced making it difficult to gain convergence in the iteration process.

3.1.2 Method II: Hu’s Invariants

Here we refer to moments as scalar quantities able to characterize a scalar field and possibly to point out some significant features. In statistics moments are widely used to describe the shape of a probability density function; in classic rigid-body mechanics to account of the mass distribution of a body, forming the inertia tensor. In mathematical terms, the moments are projections of a function onto a polynomial basis [6, 8]. General moments \(M_{pq}\) of an image I(x,y), where p, q are non-negative integers and \( r = p + q\) is called the order of the moment, are defined as:

$$\begin{aligned} M_{pq} = \int \int {p _{pq} \left( {x,y} \right) \cdot I\left( {x,y} \right) \cdot dx\,\,dy} \end{aligned}$$
(12)

Where \(p_{00} (x, y), p_{10} (x, y), . . . , p_{pq} (x, y)\), are polynomial basis functions defined in the domain. In this chapter moments of the the image are used, consequently the function I(x,y) is an image characterized by two coordinates x,y and a color value (e.g. RGB uses three values between 0 and 255 each).

A geometric moment of a discretized image is defined as a moment having the standard power basis \(p_{pq} (x, y) = x^{p} y^{q}\) . Therefore, it results:

$$\begin{aligned} m_{pq} =\sum _x {\sum _y {x^{p}\cdot y^{q}} } \cdot I\left( {x,y} \right) \end{aligned}$$
(13)

Moreover Hu’s invariants are built up through a combination of geometrical moments that show the characteristics of non-changing their values when some geometrical transformations are applied. Hu’s invariants are originally seven, but other invariants could be computed. However, higher image invariants would increase considerably their magnitude, so that they cannot be managed together with the first seven.

Only the first invariant moment has an intuitive meaning: polar moment of inertia.

In this section Hu’s invariants are used to characterize each sub-image. Even using this technique, the solution requires the inversion of the Jacobian matrix; in this case the Jacobian is not calculated through image differences, but differences on Hu’s invariants. The image is meshed into sub-images by a grid; each sub-image is represented be its set of Hu’s invariant moments. Hu’s invariants are seven, but here, to increase the discriminant power, the computed invariants are doubled: they are computed on the sub-image itself and on its negative.

The invariant moments are insensitive to translations, rotations and scaling transforms. In an index compact notation they are:

$$\begin{aligned} \begin{array}{ll} {\upvarphi }_1 &{}\!\!\!\!= m_{20} +m_{02} \\ {\upvarphi }_2 &{}\!\!\!\!= (m_{20} -m_{02} )^{2}+4 m_{11}^2 \\ {\upvarphi }_3 &{}\!\!\!\!= (m_{30} -3 m_{12} )^{2}+(3 m_{21} -m_{03} )^{2} \\ {\upvarphi }_4 &{}\!\!\!\!= (m_{30} +m_{12} )^{2}+(m_{21} -m_{03} )^{2} \\ {\upvarphi }_5 &{}\!\!\!\!= (m_{30} -3 m_{12} )(m_{30} +m_{12} )\left[ {\left( {m_{30} +m_{12} } \right) ^{2}-3 \left( {m_{21} +m_{03} } \right) ^{2}} \right] + \\ &{}\quad + (3 m_{21} -m_{03} )(m_{21} +m_{03} )\left[ {3 (m_{30} +m_{12} )^{2}-(m_{21} +m_{03} )^{2}} \right] \\ {\upvarphi }_6 &{}\!\!\!\!= (m_{20} -m_{02} )\left[ {\left( {m_{30} +m_{12} } \right) ^{2}-\left( {m_{21} +m_{03} } \right) ^{2}} \right] + \\ &{}\quad + 4 m_{11} (m_{30} +m_{12} )(m_{21} +m_{03} ) \\ {\upvarphi }_7 &{}\!\!\!\!= (3 m_{21} -m_{03} )(m_{30} +m_{12} )\left[ {\left( {m_{30} +m_{12} } \right) ^{2}-3 \left( {m_{21} +m_{03} } \right) ^{2}} \right] + \\ &{}\quad - (m_{30} +3 m_{12} )(m_{21} +m_{03} )\left[ {3 (m_{30} +m_{12} )^{2}-(m_{21} +m_{03} )^{2}} \right] \\ \end{array} \end{aligned}$$
(14)

3.2 Natural Coordinate System Applied on Elements

Both methods require the image comparison to minimize the error. To this goal it is useful referring to the natural coordinate system used in the isoparametric element formulation [16].

Their characteristics are particularly suitable because, in the natural coordinate system, all the elements, as well as in the reference picture as in the deformed one, have the same shape and dimensions (a simple square as shown in Fig. 4).

For the isoparametric four-node element, all internal points are mapped through natural coordinates r,s in the following manner:

$$\begin{aligned} \left\{ {\begin{array}{ll} x(r,s) &{}= \frac{1}{4}(1-r)(1-s) x_1 +\frac{1}{4}(1-r)(1+s) x_2 + \\ &{}\quad +\frac{1}{4}(1+r)(1-s) x_3 +\frac{1}{4}(1+r)(1+s) x_4 \\ y(r,s) &{}= \frac{1}{4}(1-r)(1-s) y_1 +\frac{1}{4}(1-r)(1+s) y_2 + \\ &{}\quad +\frac{1}{4}(1+r)(1-s) y_3 +\frac{1}{4}(1+r)(1+s) y_4 \\ \end{array}} \right. \end{aligned}$$
(15)

As a matter of fact, one of the difficulties encountered in both methods regards the change of the edges during displacement, now overtaken by using elements having a fixed domain shape, whatever is the image content. By this change of reference, an interpolation is required between the pixels in each element (only on sub-images of whole picture) and the values assumed in the r-s coordinate system. According to the isoparametric formulation, the same interpolation used to locate any internal point is adopted to evaluate internal displacements. The use of r-s coordinate system allows also to manage non-regular shaped elements. And to modify the number of unknowns considered.

3.3 Comparison Between Grouping Technique and Hu’s Invariant

In this section a comparison is proposed: (i) full pixel computation; (ii) grouping technique by varying packaging dimension; (iii) Hu’s invariant moments. All techniques have been applied on the same reference image. This image shows the surface of a granite (Fig. 13). The use of this image is due to his particular distribution of color that is a natural sort of speckle. The image is divided in \(3\times 3\) elements and 16 nodes; the dimension of a single element is \(100\times 100\) pixels. The original image is digitally deformed by \(\varepsilon _{x} = 0.02\) and \(\varepsilon _{y} = 0.01\). The (i) results (no enhancement) are obtained when the number of packets (a packet contains adjacent pixel grouped together) id equal to 10000 (number of pixels in each sub-image).

Fig. 13
figure 13

Reference undeformed image \(500\times 500\) pixel

Full size image

Several tests are performed progressively decreasing the number of packets. The lowest number of packets considered is 9, while the maximum numbers is 10000, representing the solution without any enhancement technique. Both convergence time and final error of the displacements are compared. All computations are performed on an internal processor Intel\({\circledR }\) Core i7-2600 K having 3.4 GHz.

The error is calculated through a ratio: the numerator is the sum of the displacement differences between the identified final nodal position and the theoretical one (known due to strain imposed); the denominator is the sum of the differences between the theoretical position and the initial one.

In Fig. 14 errors and convergence times are normalized by respect to the highest values encountered. Note that this relative definition of error penalizes the lower displacements and this must be kept in mind when comparing different deformation magnitudes.

Fig. 14
figure 14

Cpu Time versus error for the grouping technique for the grouping technique

Full size image
Table 5 Grouping technique performace
Full size table

As expected, the maximum errors are obtained with the minimum number of packets; the worst convergence time is obtained when no enhanced technique is used. Increasing the number of packets decreases the error convergence, but increases the calculation time and vice versa. It is possible to detect a crossing point of minimum error-time curves (Fig. 14, Table 5). It is interesting to highlight that the red curve (squares) identifies a well-defined knee, demonstrating that a strong grouping is possible while shortly affecting accuracy.

The results obtained with the method of Hu’s invariant moments are s hown in Table 6. This method does not show at the present time particularly good outcomes. The invariants allow to greatly reducing the number of equations of the system, but they do not ensure acceptable results both in terms of computing time and precision of the solution. Even the use of non-speckle images helped to gain accurate results.

However, at strain values of the order of some percent, the Hu’s invariant method works acceptably. The increase of the convergence time is mainly due to the increment in the number of iterations required to converge (Table 7).

Table 6 Hu’s invariant moments technique performance
Full size table

Further tests have been performed using the grouping technique. In particular, some tests considered large strains applied, (over 30 %). It is interesting to observe that the grouping technique is able to manage also this amount of image differences, even when the non-enhanced technique is unable to reach convergence. Thus, the use of packets helps to speed up the solution time, but it is also skillful to organize information so that the convergence capability is stronger than before. As an example, in the case analyzed and proposed in Fig. 13, presenting a strong deformation reaching 0.35 in both principal directions, calculated with 25 packages, the method returns a solution with an error close to 0.56 % and 9.84 s of convergence time, whereas when non-using packages the solution does not converge at all (Fig. 15).

Table 7 Grouping technique performance
Full size table

To validate the grouping technique, another example is performed: the image used is not a speckle, but a generic image (canvas paint in Fig. 16). In this case the deformations are not of the same magnitude of the preceding ones, but they are set to \(\varepsilon _{x} = 0.03\) and \(\varepsilon _{y} = 0.01\); much more elements are used to mesh the image. In particular a grid of \(10 \times 10\) elements, having \(50 \times 50\) pixels each is used. The study was performed both with a number of packets equal to 25, and without any convergence enhancement technique.

This latter example shows once again the convenience of the use of packets, both in terms of accuracy and computational time. This convenience is stronger and stronger when increasing the number of sub-images managed. Incidentally, it is shown that the use of packets is profitable on non-speckled images.

Fig. 15
figure 15

Example large deformed image and grid solution obtained by grouping technique

Full size image
Fig. 16
figure 16

Example deformed image and grid \(10\times 10\) solution obtained by grouping technique

Full size image

4 Conclusions

In this work it has been discussed a discretization technique that is able to account of off-plane displacements of a surface as well as in-plane deformations. For both circumstances a differential method to determine the displacement field is presented. In the chapter two different procedures to reduce the number of equations are discussed. The first method consists on the grouping of the Jacobian matrix. Despite the reduction of the number of equations, the system is always over-determined, the solution converges with an error decreasing while increasing the number of packets. This method is robust and reliable and allows convergence even when very high deformations occur.

A possible use is to apply this procedure as a preliminary calculation in order to approach the exact solution, then refining the results by omitting packets grouping. The second method uses Hu’s invariants for the assembly of the Jacobian matrix. The number of the equations is reduces to the number of Hu’s invariant moments. This second method designed to enhance the convergence is not as reliable as the previous one; as a matter of fact, even though the number of equations is lower than in the grouping method, the iterations required increase significantly. Furthermore, the increase in the total time is not accompanied by accuracy growth.