Quantum-Behaved Particle Swarm Optimization with Diversity-Maintained

Abstract

Quantum-behaved particle swarm optimization (QPSO) algorithm is a global-convergence-guaranteed algorithm, which outperforms original PSO in search ability but has fewer parameters to control. But QPSO algorithm is to be easily trapped into local optima as a result of the rapid decline in diversity. So this paper describes diversity-maintained into QPSO (QPSO-DM) to enhance the diversity of particle swarm and then improve the search ability of QPSO. The experiment results on benchmark functions show that QPSO-DM has stronger global search ability than QPSO and standard PSO.

1 Introduction

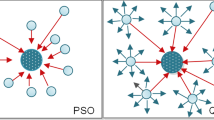
Particle swarm optimization (PSO) is a kind of stochastic optimization algorithms proposed by Kennedy and Eberhart [1] that can be easily implemented and is computationally inexpensive. The core of PSO is based on an analogy of the social behavior of flocks of birds when they search for food. PSO has been proved to be an efficient approach for many continuous global optimization problems. However, as demonstrated by Van Den Bergh [2], PSO is not a global-convergence-guaranteed algorithm because the particle is restricted to a finite sampling space for each of the iterations. This restriction weakens the global search ability of the algorithm and may lead to premature convergence in many cases.

Several authors developed strategies to improve on PSO. Clerc [3] suggested a PSO variant in which the velocity to the best point found by the swarm is replaced by the velocity to the current best point of the swarm, although he does not test this variant. Clerc [4] and Zhang et al. [5] dynamically change the size of the swarm according to the performance of the algorithm. Eberhart and Shi [6], He et al. [7] adopted strategies based on dynamically modifying the value of the PSO parameter called inertia weight. Various other solutions have been proposed for preventing premature convergence: objective functions that change over time [8]; noisy evaluation of the function objective [9]; repulsion to keep particles away from the optimum [10]; dispersion between particles that are too close to one another [11]; reduction in the attraction of the swarm center to prevent the particles clustering too tightly in one region of the search space [12]; hybrids with other metaheuristic such as genetic algorithms [13]; ant colony optimization [14], etc. An up-to-date overview of the PSO is introduced in [15].

Recently, a new variant of PSO, called quantum-behaved particle swarm optimization (QPSO) [16, 17], which is inspired by quantum mechanics and particle swarm optimization model. QPSO has only the position vector without velocity, so it is simpler than standard particle swarm optimization algorithm. Furthermore, several benchmark test functions show that QPSO performs better than standard particle swarm optimization algorithm. Although the QPSO algorithm is a promising algorithm for the optimization problems, like other evolutionary algorithm, QPSO also confronts the problem of premature convergence and decreases the diversity in the latter period of the search. Therefore, a lot of revised QPSO algorithms have been proposed since the QPSO had emerged. In Sun et al. [18], the mechanism of probability distribution was proposed to make the swarm more efficient in global search. Simulated annealing is further adopted to effectively employ both the ability to jump out of the local minima in simulated annealing and the capability of searching the global optimum in QPSO algorithm [19]. Mutation operator with Gaussian probability distribution was introduced to enhance the performance of QPSO in Coelho [20]. Immune operator based on the immune memory and vaccination was introduced into QPSO to increase the convergent speed using the characteristic of the problem to guide the search process [21].

In this chapter, QPSO with diversity-maintained (QPSO-DM) is introduced. This strategy is to prevent the diversity of particle swarm declining in the search of later stage.

The rest of the chapter is organized as follows. In Sect. 2, the principle of the PSO is introduced. The concept of QPSO is presented in Sect. 3, and the QPSO with diversity-maintained is proposed in Sect. 4. Section 5 gives the numerical results on some benchmark functions and discussion. Some concluding remarks and future work are presented in the last section.

2 PSO Algorithm

In the original PSO with M individuals, each individual is treated as an infinitesimal particle in the D-dimensional space, with the position vector and velocity vector of particle i, $X_{i} (t) = (X_{i1} (t),\;X_{i2} (t),\; \ldots ,\;X_{iD} (t))$, and $V_{i} (t) = (V_{i1} (t),V_{i2} (t), \ldots ,V_{iD} (t))$. The particle moves according to the following equations:

$$ V_{ij} (t + 1) = V_{ij} (t) + c_{1} \cdot r_{1} \cdot (P_{ij} (t) - X_{ij} (t)) + c_{2} \cdot r_{2} \cdot (P_{gj} (t) - X_{ij} (t)) $$

(1)

$$ X_{ij} (t + 1) = X_{ij} (t) + V_{ij} (t + 1) $$

(2)

for $i = 1,2, \ldots \;M;j = 1,2\; \ldots ,D$. The parameters $c_{1}$ and $c_{2}$ are called the acceleration coefficients. Vector $P_{i} = (P_{i1} ,\;P_{i2},\; \ldots ,\;P_{iD} )$ known as the personal best position is the best previous position (the position giving the best fitness value so far) of particle i; vector $P_{g} = (P_{g1} \;,P_{g2}\; , \ldots ,\;P_{gD} )$ is the position of the best particle among all the particles and is known as the global best position. The parameters $r_{1}$ and $r_{2}$ are two random numbers distributed uniformly in (0, 1), that is, $r_{1} ,\;r_{2} \sim U(0,\;1)$. Generally, the value of V _ij is restricted in the interval $[ - V_{\hbox{max} } ,\;V_{\hbox{max} } ]$.

Many revised versions of PSO algorithm are proposed to improve the performance since its origin in 1995. Two most important improvements are the version with an Inertia Weight [22] and a Constriction Factor [23]. In the inertia-weighted PSO, the velocity is updated by using

$$ V_{ij} (t + 1) = w \cdot V_{ij} (t) + c_{1} \cdot r_{1} (P_{ij} (t) - X_{ij} (t)) + c_{2} \cdot r_{2} \cdot (P_{gj} - X_{ij} (t)) $$

(3)

while in the Constriction Factor model, the velocity is calculated by using

$$ V_{ij} (t + 1) = K \cdot [V_{ij} (t) + c_{1} \cdot r_{2} \cdot (P_{ij} (t) - X_{ij} (t)) + c_{2} \cdot r_{2} \cdot (P_{gj} - X_{ij} (t))] $$

(4)

where

$$ k = \frac{2}{{\left| {2 - \varphi - \sqrt {\varphi^{2} - 4\phi } } \right|}}\quad \varphi = c_{1} + c_{2}, \quad \varphi > 4 $$

(5)

The inertia-weighted PSO was introduced by Shi and Eberhart [6] and is known as the standard PSO.

3 QPSO Algorithm

Trajectory analyses in Clerc and Kennedy [24] demonstrated the fact that convergence of PSO algorithm may be achieved if each particle converges to its local attractor $p_{i} = (p_{i1} ,p_{i2} , \ldots \;p_{iD} )$ with coordinates

$$ p_{ij} (t) = (c_{1} r_{1} P_{ij} (t) + c_{2} r_{2} P_{gj} (t))/(c_{1} r_{1} + c_{2} r_{2} ),\,{\text{or}}\,p_{ij} (t) = \varphi \cdot P_{ij} (t) + (1 - \varphi ) \cdot P_{gj} (t) $$

(6)

where $\varphi = c_{1} r_{1} /(c_{1} r_{1} + c_{2} r_{2} ).$ It can be seen that the local attractor is a stochastic attractor of particle i that lies in a hyper-rectangle with $P_{i}$ and $P_{g}$ being two ends of its diagonal. We introduce the concepts of QPSO as follows.

Assume that each individual particle moves in the search space with a $\delta$potential on each dimension, of which the center is the point $p_{ij}$. For simplicity, we consider a particle in one-dimensional space, with point p the center of potential. Solving Schrödinger equation of one-dimensional $\delta$ potential well, we can get the probability distribution function $D(x) = e^{{ - 2\left| {p - x} \right|/L}} .$ Using Monte Carlo method, we obtain

$$ x = p \pm \frac{L}{2}\ln ({1 \mathord{\left/ {\vphantom {1 u}} \right. \kern-0pt} u}),\;\;u\sim U(0,\;1) $$

(7)

The above is the fundamental iterative equation of QPSO.

In Sun et al. [17], a global point called Mainstream Thought or Mean Best Position of the population is introduced into PSO. The mean best position, denoted as C, is defined as the mean of the personal best positions among all particles. That is

$$ C(t) = (C_{1} (t),\;C_{2} (t),\; \ldots ,\;C_{D} (t)) = \left( {\begin{array}{*{20}c} {\frac{1}{M}\sum\limits_{i = 1}^{M} {P_{i1} (t)} ,} & {\begin{array}{*{20}c} {\frac{1}{M}\sum\limits_{i = 1}^{M} {P_{i2} (t)} ,} & { \ldots ,} \\ \end{array} } & {\frac{1}{M}\sum\limits_{i = 1}^{M} {P_{iD} (t)} } \\ \end{array} } \right) $$

(8)

where M is the population size and $P_{i}$ is the personal best position of particle i. Then, the value of L is evaluated by $L = 2\alpha \cdot \left| {C_{j} (t) - X_{ij} (t)} \right|$, and the position is updated by

$$ X_{ij} (t + 1) = p_{ij} (t) \pm \alpha \cdot \left| {C_{j} (t) - X_{ij} (t)} \right| \cdot \ln (1/u) $$

(9)

where parameter $\alpha$ is called Contraction–Expansion (CE) Coefficient, which can be tuned to control the convergence speed of the algorithms. Generally, we always call the PSO with Eq. (9) quantum-behaved particle swarm optimization (QPSO). In most cases, $\alpha$ decrease linearly from can be controlled to $\alpha_{0} \;{\text{to}}\;\alpha_{1} (\alpha_{0} < \alpha_{1} )$.We outline the procedure of the QPSO algorithm as follows:

Procedure of the QPSO algorithm:

• Step 1: Initialize the population;

• Step 2: Computer the personal position and global best position;

• Step 3: Computer the mean best position C;

• Step 4: Properly select the value of $\alpha$;

• Step 5: Update the particle position according to Eq. (9);

• Step 6: While the termination condition is not met, return to Step 2;

• Step 7: Output the results.

4 QPSO-DM Algorithm

QPSO is a promising optimization problem solver that outperforms PSO in many real application areas. First of all, the introduced exponential distribution of positions makes QPSO global convergent. In the QPSO algorithm in the initial stage of search, as the particle swarm initialization, its diversity is relatively high. In the subsequent search process, due to the gradual convergence of the particle, the diversity of the population continues to decline. As the result, the ability of local search ability is continuously enhanced, and the global convergence ability is continuously weakened. In early and middle search, reducing the diversity of particle swarm optimization for contraction efficiency improvement is necessary; however, in late stage of search, because the particles are gathered in a relatively small range, particle swarm diversity is very low, the global search ability becomes very weak, the ability for a large range of search has been very small, and the phenomenon of premature will occur in this algorithm.

To overcome this shortcoming, we introduce diversity-maintained into QPSO.

The population diversity of the QPSO-DM is denoted as ${\text{diversity}}(p{\text{best}})$ and is measured by average Euclidean distance from the particle’s personal best position to the mean best position, namely

$$ {\text{diversisty}}(p{\text{best}}) = \frac{1}{M \cdot \left| A \right|}\sum\limits_{i = 1}^{M} {\sqrt {\sum\limits_{j = 1}^{D} {(p{\text{best}}_{i,j} -\mathop {p{\text{best}}_{j} }\limits^{\_} )} } } $$

(10)

where M is the population of the particle, $\left| A \right|$ is the length of longest the diagonal in the search pace, and D is the dimension of the problem. Hence, we may guide the search of the particles with the diversity measures when the algorithm is running.

In the QPSO-DC algorithm, only low-bound $d_{\text{low}}$ is set for ${\text{diversity}}(p{\text{best}})$ to prevent the diversity from constantly decreasing. The procedure of the algorithm is as follows. After initialization, the algorithm is running in convergence mode. In process of convergence, the convergence mode is realized by Contraction–Expansion (CE) Coefficient α. On the course of evolution, if the diversity measure ${\text{diversity}}(p{\text{best}})$ of the swarm drops to below the low-bound $d_{\text{low}}$, the particle swarm turns to be in explosion mode in which the particles are controlled to explode to increase the diversity until it is larger than $d_{\text{low}}$.

5 Experiment Results and Discussion

To test the performance of the QPSO with diversity-maintained (QPSO-DM), six widely known benchmark functions listed in Table 1 are tested for comparison with standard PSO (SPSO), QPSO. These functions are all minimization problems with minimum objective function values as zeros. The initial range of the population listed in Table 2 is asymmetry as used in Shi and Eberhart [25]. Table 2 also lists $V_{\hbox{max} }$ for SPSO. The fitness value is set as function value, and the neighborhood of a particle is the whole population.

Table 1 Expression of the five tested benchmark functions

Table 2 The initial range of population for all the tested algorithms and V_max for spso

As in Angeline [22], for each function, three different dimension sizes are tested. They are dimension sizes 10, 20, and 30. The max number of generations is set as 1,000, 1,500, and 2,000 corresponding to the dimensions 10, 20, and 30 for first six functions, respectively. The maximum generation for the last function is 2,000. In order to investigate whether the QPSO-DM algorithm is good or not, different population sizes are used for each function with different dimension. They are population sizes 20, 40, and 80. For SPSO, the acceleration coefficients are set to be $c_{1} = c_{2} = 2$, and the inertia weight is decreasing linearly from 0.9 to 0.4 as in Shi and Eberhart [25]. In experiments for QPSO, the value of CE Coefficient varies from 1.0 to 0.5 linearly over the running of the algorithm as in [18], while in QPSO-DM, the value of CE Coefficient is listed in Table 3. From the Table 3, we also obtain the CE cofficient of QPSO-DM decreases from 0.8–0.5 linearly. We had 50 trial runs for every instance and recorded mean best fitness and standard deviation.

Table 3 Parameter value of QPSO-dM

The mean values and standard deviations of best fitness values for 50 runs of each function are recorded in Tables 4, 5, 6, 7, and 8.

Table 4 Numerical results on sphere function

Table 5 Numerical results on Rosenbrock function

Table 6 Numerical results on rastrigrin function

Table 7 Numerical results on ackley function

Table 8 Numerical results on schwefel function

The results show that both QPSO and QPSO-DM are superior to SPSO except on Schwefel and Shaffer’s f6 function. On Sphere Function, the QPSO works better than QPSO-DM when the warm size is 40 and dimension is 10, and when the warm size is 80 and dimension is 20. Except for the above two instances, the best result is QPSO-DM. The Rosenbrock function is a monomodal function, but its optimal solution lies in a narrow area that the particles are always apt to escape. The experiment results on Rosenbrock function show that the QPSO-DM outperforms the QPSO. Rastrigrin function and Griewank function are both multimodal and usually tested for comparing the global search ability of the algorithm. On Rastrigrin function, it is also shown that the QPSO-DM generated best results than QPSO. On Griewank function, QPSO-DM has better performance than QPSO and PSO algorithms. On Ackley function, QPSO-DM has best performance when the dimension is 10; except for these, the QPSO-DM has minimal value. On the Schwefel function, SPSO has the best performance in any situation. QPSO-DM is better than QPSO. Generally speaking, the QPSO-DM has better global search ability than SPSO and QPSO.

Figure 1 shows the convergence process of the three algorithms on the first four benchmark functions with dimension 30 and swarm size 40 averaged on 50 trail runs. It is shown that, although QPSO-DM converges more slowly than the QPSO during the early stage of search, it may catch up with QPSO at later stage and could generate better solutions at the end of search.

Fig. 1

Convergence process of the three algorithms on the first four benchmark functions with dimension 30 and swarm size 40 averaged on 50 trail runs

From the results above in the tables and figures, it can be concluded that the QPSO-DM has better global search ability than SPSO and QPSO.