Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Neutron star crust is a possible site where neutron rich heavy nuclei might reside. Extreme physical conditions exist at the crust of a neutron star. The temperature is \(\sim 10^{10}\) K and the density varies from \(10^4\)–\(10^{14}\) g/cm\(^3\) there. Recently, it was observed that certain neutron stars called magnetars had surface magnetic fields \(\sim 10^{15}\) G. The internal fields could be several times higher than the surface fields of magnetars. Soft gamma repeaters (SGRs) are suitable candidates for magnetars [1–3]. Giant flares were observed from SGRs in several cases. Those giant flare events are thought to be the results of star quakes in magnetars. This might be attributed to the tremendous magnetic stress due to the evolving magnetic field leading to cracks in the crust. Quasi-periodic oscillations discovered in three giant flares are the evidences of torsional shear mode oscillations in magnetar crusts.

Such strong magnetic fields in magnetars are expected to influence charged particles such as electrons in the crust through Landau quantization. The effects of strong magnetic fields on dense matter in neutron star interior were studied earlier [4, 5]. It was also noted that atoms, molecules became more bound in a magnetic field [6]. In this article, we discuss the effects of strongly quantising magnetic fields on compositions and equation of state of the ground state matter in neutron star crusts and its connection to torsional shear mode oscillations.

We organise the article in the following way. Neutron star crusts in strong magnetic fields are described in Sects. 2, 3 and 4. Torsional shear mode oscillations of magnetars are discussed in Sect. 5. Finally, we summarise in Sect. 6.

2 Crusts in Strong Magnetic Fields

We investigate compositions and equations of state (EoS) of outer and inner crusts in strong magnetic fields. Nucleons are bound in nuclei in the outer crust. Nuclei are immersed in a uniform background of electron gas which becomes relativistic beyond \(10^7\) g/cm\(^3\). Neutrons start to drip out of nuclei at higher densities. This is the beginning of the inner crust. In this case, nuclei are embedded both in electron and neutron gases. Magnetic fields may influence the ground state properties of crusts either through magnetic field and nuclear magnetic moment interaction or through Landau quantisation of electrons. In a magnetic field \(\sim 10^{17}\) G, magnetic field and nuclear magnetic moment interaction would not produce any significant change. However such a strong magnetic field is expected to influence charged particles such as electrons in the crust through Landau quantization. Our main focus is to study the effects of Landau quantisation on the ground state properties of neutron star crusts. Later we discuss shear mode frequencies using our results of magnetised neutron star crusts.

2.1 Landau Quantisation of Electrons

We consider electrons are noninteracting and placed under strongly quantising magnetic fields. In the presence of a magnetic field, the motion of electrons is quantized in the plane perpendicular to the field. We do not consider Landau quantisation of protons because magnetic fields in question in this calculation are below the critical field for protons. However, protons in nuclei would be influenced by a magnetic field through the charge neutrality condition. We take the magnetic field (\(\varvec{B}\)) along Z-direction and assume that it is uniform throughout the inner crust. If the field strength exceeds a critical value \(B_c\,=\,m_e^2/e\simeq 4.414\times 10^{13}\) G, then electrons become relativistic [6]. The energy eigenvalue of relativistic electrons in a quantizing magnetic field is given by

$$\begin{aligned} E_e(\nu ,p_z)=\left[ p_z^2+m_e^2 + 2 e B \nu \right] ^{1/2} ~, \end{aligned}$$
(1)

where \(p_z\) is the Z-component of momentum, \(\nu \) is the Landau quantum number. The Fermi momentum of electrons, \(p_{F_{e,\,\nu }}\), is obtained from the electron chemical potential in a magnetic field

$$\begin{aligned} p_{F_{e,\,\nu }}= \left[ {\mu _e}^2-m_e^2 - 2 e B \nu \right] ^{1/2}~. \end{aligned}$$
(2)

The number density of electrons in a magnetic field is calculated as

$$\begin{aligned} n_e=\frac{eB}{2\pi ^2}\sum _{\nu \,=\,0}^{\nu _{max}}g_{\nu }p_{F_{e,\,\nu }}~, \end{aligned}$$
(3)

where the spin degeneracy is \(g_\nu = 1\) for the lowest Landau level (\(\nu =0\)) and \(g_\nu = 2\) for all other levels.

The maximum Landau quantum number (\(\nu _{max}\)) is obtained from

$$\begin{aligned} \nu _{max}=\frac{{\mu _e}^2-m_e^2}{2eB}~. \end{aligned}$$
(4)

The energy density of electrons is,

$$\begin{aligned} \varepsilon _e= \frac{eB}{4\pi ^2} \sum _{\nu \,=\,0}^{\nu _{max}}g_{\nu } \left( p_{F_{e,\,\nu }}\mu _e + (m_e^2 + 2 e B \nu ) \ln \frac{p_{F_{e,\,\nu }}+\mu _e}{\sqrt{(m_e^2 + 2 e B \nu )}}\right) ~. \end{aligned}$$
(5)

Similarly the pressure of the electron gas is determined by

$$\begin{aligned} P_e= \frac{eB}{4\pi ^2} \sum _{\nu \,=\,0}^{\nu _{max}}g_{\nu } \left( p_{F_{e,\,\nu }}\mu _e - (m_e^2 + 2 e B \nu ) \ln \frac{p_{F_{e,\,\nu }}+\mu _e}{\sqrt{(m_e^2 + 2 e B \nu )}}\right) ~. \end{aligned}$$
(6)

3 Magnetic BPS Model of Outer Crust Revisited

We describe the BPS model in the presence of strong magnetic fields \(B\sim 10^{16}\)G to determine the sequence of equilibrium nuclei and the equation state of the outer crust [7, 8]. Nuclei are arranged in a bcc lattice in the outer crust. Here we adopt the Wigner-Seitz (WS) approximation and replace each lattice volume by a spherical cell which contains one nucleus at the center. Further each cell is to be charge neutral such that equal numbers of protons and electrons are present there. The Coulomb interaction among cells is neglected. An equilibrium nucleus (A, Z) at a given pressure P is obtained by minimising the Gibbs free energy per nucleon with respect to A and Z. In this calculation, we modify the magnetic BPS model including the finite size effect in the lattice energy and adopting recent experimental and theoretical mass tables. The total energy density of the system is given by

$$\begin{aligned} E_{tot} = n_N (W_N+ W_L)+ \varepsilon _e~. \end{aligned}$$
(7)

The energy of the nucleus (including rest mass energy of nucleons) is

$$\begin{aligned} W_N = m_n (A - Z) + m_p Z - bA~, \end{aligned}$$
(8)

where \(n_N\) is the number density of nuclei, \(b\) is the binding energy per nucleon. Experimental nuclear masses are obtained from the atomic mass table compiled by Audi, Wapstra and Thibault [9]. For the rest of nuclei we use the theoretical extrapolation of Möller et al. [10]. \(W_L\) is the lattice energy of the cell and is given by

$$\begin{aligned} W_L= -\frac{9}{10}\frac{Z^2e^2}{r_C}\left( 1-\frac{5}{9} \left( \frac{r_N}{r_C}\right) ^2\right) ~. \end{aligned}$$
(9)

Here \(r_C\) is the cell radius and \(r_N\simeq r_0A^{1/3}\) (\(r_0\simeq 1.16\) fm) is the nuclear radius. The first term in \(W_L\) is the lattice energy for point nuclei and the second term is the correction due to the finite size of the nucleus (assuming a uniform proton charge distribution in the nucleus). Further \(\varepsilon _e\) is the electron energy density as given by Eq. (5) and P is the total pressure of the system given by

$$\begin{aligned} P=P_e+\frac{1}{3}W_Ln_N~, \end{aligned}$$
(10)

where \(P_e\) is the pressure of electron gas in a magnetic field as given by Eq. (6).

Fig. 1
figure 1

Gibbs free energy per nucleon is plotted with mass density for zero magnetic field (left panel) and \(B_{*}=10^3\) (right panel). Equilibrium nuclei are shown with solid symbols in both panels

Full size image

The Gibbs free energy per nucleon is

$$\begin{aligned} g = \frac{E_{tot} + P}{n} = \frac{W_N + 4/3 W_L + Z \mu _e}{A}~, \end{aligned}$$
(11)

where \(n\) is the total baryon number density.

At a fixed pressure \(P\), we minimise \(g\) varying \(A\) and \(Z\) of a nucleus. The sequence of equilibrium nuclei and their corresponding free energies are shown in Fig. 1. Here we define \(B_{*} = B/B_c\). The left panel shows results for \(B=0\) and the right panel corresponds to \(B_{*}=10^3\). It is evident from the figure that some nuclei disappear and new nuclei appear under the influence of strong magnetic fields. It is attributed to the phase space modification of electrons due to Landau quantisation which enhances the electron number density [8].

4 Inner Crust in Quantizing Magnetic Fields

Now we describe the ground properties of matter of inner crusts in presence of strong magnetic fields using the Thomas-Fermi (TF) model at zero temperature. Inner crust nuclei are immersed in a nucleonic gas as well as a uniform background of electrons. Furthermore, nuclei are arranged in a bcc lattice. As in the case of outer crust, we again adopt the Wigner-Seitz (WS) approximation in this calculation. Here each cell is taken to be charge neutral and the Coulomb interaction between cells is neglected. Electrons are uniformly distributed within a cell. The system is in \(\beta \)-equilibrium. We assume that the system is placed in a uniform magnetic field. Though electrons are directly affected by strongly quantizing magnetic fields, protons in the cell are influenced through the charge neutrality condition [11]. The interaction of nuclear magnetic moment with the field is not considered because it is negligible in a magnetic field below \(10^{18}\) G [12].

The spherical cell in the WS approximation does not define a nucleus. We exploit the prescription of Bonche, Levit and Vautherin [13, 14] to subtract the gas part from the cell and obtain the nucleus. It was shown that the TF formalism at finite temperature generated two solutions [15]—one for the nucleus plus neutron gas and the other representing the neutron gas. The nucleus is obtained as the difference of two solutions. This formalism is adopted in our calculation at zero temperature as described below.

The thermodynamic potentials for nucleus plus gas (NG) and only gas (G) phases are defined as [13, 14]

$$\begin{aligned} \Omega = {\fancyscript{F}} - \sum _{q\,=\,n,\,p} \mu _q n_q~, \end{aligned}$$
(12)

where \(\fancyscript{F}\), \(\mu _q\) and \(n_q\) are the free energy density, baryon chemical potential and number density, respectively. The nucleus plus gas solution coincides with the gas solution at large distance i.e. \(\Omega _{NG} = \Omega _{G}\). The free energy which is a function of baryon number density and proton fraction (\(Y_p\)), is defined as [11]

$$\begin{aligned} {\fancyscript{F}}(n_q,Y_p) = \int [{\fancyscript{H}} + \varepsilon _c + \varepsilon _e] d\mathbf{r}~. \end{aligned}$$
(13)

The nuclear energy density is calculated using the Skyrme nucleon-nucleon interaction and it is given by [16–18]

$$\begin{aligned} {\fancyscript{H}}(r)&=\frac{\hbar ^2}{2m_n^*}\tau _n +\frac{\hbar ^2}{2m_p^*}\tau _p+ \frac{1}{2}t_0\left[ \left( 1+\frac{x_0}{2}\right) n^2-\left( x_0+ \frac{1}{2}\right) \left( n^2_n+n^2_p\right) \right] \nonumber \\&\quad -\frac{1}{16}\left[ t_2\left( 1+\frac{x_2}{2}\right) -3t_1\left( 1+\frac{x_1}{2}\right) \right] (\nabla n)^2\nonumber \\&\quad -\frac{1}{16}\left[ 3t_1\left( x_1+\frac{1}{2}\right) +t_2\left( x_2+\frac{1}{2} \right) \right] \left[ (\nabla n_n)^2+(\nabla n_p)^2\right] \nonumber \\&\quad +\frac{1}{12}t_3 n^\alpha \left[ \left( 1+\frac{x_3}{2}\right) n^2 -\left( x_3+\frac{1}{2}\right) \left( n_n^2+ n_p^2\right) \right] ~, \end{aligned}$$
(14)

and the effective nucleon mass

$$\begin{aligned} \frac{m}{m_q^*(r)}&=1+\frac{m}{2\hbar ^2}\left\{ \left[ t_1\left( 1+ \frac{x_1}{2}\right) +t_2\left( 1+\frac{x_2}{2}\right) \right] \right. n \nonumber \\&\quad +\left. \left[ t_2\left( x_2+\frac{1}{2}\right) -t_1\left( x_1+\frac{1}{2} \right) \right] n_q\right\} ~, \end{aligned}$$
(15)

where total baryon density is \(n = n_n + n_p\).

The direct parts of Coulomb energy densities for the nucleus plus gas and gas phases follow from [11, 19]

$$\begin{aligned} \varepsilon ^{NG}_c (r)&=\frac{1}{2} (n^{NG}_p(r)-n_e) \int \frac{e^2}{\mid \mathbf{r}-\mathbf{r^{\prime }}\mid } (n^{NG}_p(r^{\prime })-n_e)d\mathbf{r^{\prime }}\nonumber \\ \varepsilon ^{G}_c (r)&=\frac{1}{2} (n^{G}_p(r)-n_e) \int \frac{e^2}{\mid \mathbf{r}-\mathbf{r^{\prime }}\mid } (n^{G}_p(r^{\prime })-n_e)d\mathbf{r^{\prime }}\nonumber \\&\quad +n^{N}_p(r) \int \frac{e^2}{\mid \mathbf{r}-\mathbf{r^{\prime }}\mid } (n^{G}_p(r^{\prime })-n_e)d\mathbf{r^{\prime }}~, \end{aligned}$$
(16)

where \(n_p^{NG}\) and \(n_p^G\) are proton densities in two respective phases. The exchange parts of coulomb energy densities are small and neglected in this calculation.

The average electron chemical potential in a magnetic field given by Eq. (2) is modified to [11]

$$\begin{aligned} \mu _e = \left[ p_{F_{e,\,\nu }}(\nu )^2+ m_e^2 + 2 eB \nu \right] ^{1/2} - \langle V^c(r)\rangle ~, \end{aligned}$$
(17)

where \(\langle V^{c}(r)\rangle \) denotes the average single particle Coulomb potential and for both phases it is given by

$$\begin{aligned} V^c(r) = \int \left[ n^{NG}_p(r^{\prime })-n_e\right] \frac{e^2}{\mid {\mathbf{r} -\mathbf{r^{\prime }}}\mid } d\mathbf{r^{\prime }}~. \end{aligned}$$
(18)

The density profiles of neutrons and protons with or without magnetic fields are obtained by minimising the thermodynamic potential in the TF approximation

$$\begin{aligned} \frac{\delta \Omega _{NG}}{\delta n^{NG}_q}&= 0~,\nonumber \\ \frac{\delta \Omega _{G}}{\delta n^{G}_q}&= 0~, \end{aligned}$$
(19)

with the condition of number conservation of each species from

$$\begin{aligned} Z_{cell}&= \int n_p^{NG}(r)d\mathbf{r}~,\nonumber \\ N_{cell}&= \int n_n^{NG}(r)d\mathbf{r}~, \end{aligned}$$
(20)

where \(N_{cell}\) and \(Z_{cell}\) are neutron and proton numbers in the cell, respectively.

We obtain the mass number \(A = N +Z\) and atomic number using the subtraction procedure as

$$\begin{aligned} Z&= \int \left[ n_p^{NG}(r)- n_p^G(r)\right] d\mathbf{r}~,\nonumber \\ N&= \int \left[ n_n^{NG}(r)- n_n^G(r)\right] d\mathbf{r}~. \end{aligned}$$
(21)
Fig. 2
figure 2

Proton fraction (left panel) and mass and atomic numbers of equilibrium nuclei (right panel) are plotted with average baryon density for different magnetic field strengths and Skyrme interaction parameter sets

Full size image

Here we again obtain the equilibrium nucleus at each density by minimising the free energy of the nuclear cluster in the cell along with charge neutrality and \(\beta \)-equilibrium conditions [11]. In the left panel of Fig. 2, proton fraction is shown for \(B=0\) and \(B_{*} = 10^4\). Protons are influenced by the Landau quantisation of electrons through charge neutrality condition. At lower densities, only the zeroth Landau level is populated by electrons whereas a few Landau levels are populated above density 0.005 fm\(^{-3}\) for \(B_{*} = 10^4\) i.e. 4.414\(\times 10^{17}\) G. This is reflected in the proton fraction which rises hugely at lower densities and approaches to the zero field case at higher densities. Further we estimate the effects of different parameter sets of Skyrme interaction on the proton fraction. It is noted that the SLy4 set [20] results in higher proton fraction due to the stiffer density dependence of the symmetry energy at sub-saturation densities than that of the SkM set.

We exhibit mass and atomic numbers of equilibrium nuclei after subtraction of free neutrons as a function of average baryon density in the right panel of Fig. 2. Results are obtained for \(B=0\) and \(B_{*}=10^4\). Besides SkM and SLy4 parameter sets, we also exploit Sk272 [21] parameter set for this calculation. In all three cases, mass and atomic numbers are higher than zero field cases as long as only the zeroth Landau level is populated. However, the situation is changed at higher densities when electrons jump from the zeroth Landau level to the first level. This leads to jumps in mass and atomic numbers in nuclei as noted for the SLy4 set. Further, the variation of parameters for nucleon-nucleon interaction affects mass and atomic numbers of nuclei as it is evident from the figure. We also note that the free energy of the ground state matter in strong magnetic fields is reduced and becomes more bound compared with the field free case.

5 Shear Mode Oscillations in Magnetars

Giant x-ray flares caused by the tremendous magnetic stress on the crust of magnetars were observed in several cases. Star quakes associated with these giant flares excite seismic oscillations. Quasi-periodic oscillations (QPOs) were found in the decaying tail of giant flares from SGR 1900+14 and SGR 1806-20. Those QPOs were identified as shear mode oscillations of magnetar crusts [3, 22]. Frequencies of the observed QPOs ranged from 18 to 1800 Hz.

Shear mode frequencies are sensitive to the shear modulus of neutron star crust. The shear modulus is again strongly dependent on the composition of neutron star crust. It might be possible to constrain the properties of neutron star crusts by studying the observed frequencies of QPOs. Torsional shear mode oscillations were investigated both in Newtonian gravity [23, 24] and general relativity [25–27]. In both cases, it was assumed that the magnetised crust was decoupled from the fluid core.

Here we describe the calculation of shear mode frequencies adopting the model of Sotani et al. [26]. In this case, we study torsional shear oscillations of spherical and non-rotating relativistic stellar models. The metric used here has the form,

$$\begin{aligned} ds^2 = - e^{2\Phi } dt^2 + e^{2\Lambda } dr^2 + r^2 \left( d{\theta }^2 + \sin ^2{\theta } d{\phi }^2 \right) ~. \end{aligned}$$
(22)

The equilibrium models are obtained by solving Tolman-Oppenheimer-Volkoff equation. Next the equilibrium star is assumed to be endowed with a strong dipole magnetic field [26]. The deformation in the equilibrium star for magnetic fields \(\sim 10^{16}\) G is neglected. Torsional shear modes are the results of material velocity oscillations. These modes are incompressible and do not result in density perturbation in equilibrium stars. Consequently, this leads to negligible metric perturbations and justifies the use of the relativistic Cowling approximation [26]. The relevant perturbed matter quantity for shear modes is the \(\phi \)-component of the perturbed four velocity \(\partial {u^{\phi }}\) [26]

$$\begin{aligned} \partial {u^{\phi }} = e^{-\phi } \partial _t {\fancyscript{Y}}(t,r) {\frac{1}{\sin {\theta }}}{\partial _{\theta }} P_l(\cos {\theta })~, \end{aligned}$$
(23)

where \(\partial _t\) and \(\partial _{\theta }\) correspond to partial derivatives with respect to time and \(\theta \), respectively, \(P_l(\cos {\theta })\) is the Legendre polynomial of order \(\ell \) and \({\fancyscript{Y}}(t,r)\) is the angular displacement of the matter. The perturbation equation is obtained from the linearised equation of motion. Finally, we estimate eigenfrequencies by solving two first order differential equations Eqs. (69) and (70) of Sotani et al. [26].

Now we study the dependence of shear mode frequencies on the compositions of magnetised crusts which are already described in Sects. 3 and 4. Earlier calculations were performed with non-magnetised crusts [3, 26–28]. One important input for the shear mode calculation is the knowledge of shear modulus of the magnetised crust. Here we adopt the expression of shear modulus as given by [29, 30]

$$\begin{aligned} \mu = 0.1194 \frac{n_i (Ze)^2}{a}~, \end{aligned}$$
(24)

where \(a = 3/(4 \pi n_i)\), \(Z\) is the atomic number of a nucleus and \(n_i\) is the ion density. This zero temperature form of the shear modulus was obtained by assuming a bcc lattice and performing directional averages [31]. Later the dependence of the shear modulus on temperature was investigated with Monte Carlo sampling technique by Strohmayer et al. [30]. However we use the zero temperature shear modulus of Eq. (24) in this calculation.

Fig. 3
figure 3

Shear modulus is plotted as a function of normalised distance for different magnetic field strengths (left panel) and shear mode frequencies are plotted with different \(\ell \) values for a neutron star mass of 1.4 \(M_{\odot }\) and \(B= 4 \times 10^{14}\) G (right panel)

Full size image

We calculate the shear modulus using Eq. (24) and the compositions and equations of state of magnetised crusts obtained in Sects. 3 and 4. This is shown as a function of normalised distance with respect to radius (\(R\)) of the star for different field strengths \(B=0\), \(B_{*}=10^3\) and \(B_{*}=10^4\) and a neutron star mass of 1.4 \(M_{\odot }\) in the left panel of Fig. 3. Shear modulus increases initially with decreasing distance and drops to zero at the crust-core boundary. For \(B_{*}=10^4\) i.e. 4.414\(\times 10^{17}\) G or more, the shear modulus is enhanced appreciably compared with the zero field case.

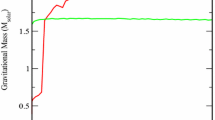
It was argued that shear mode frequencies are sensitive to shear modulus [3, 28]. We perform our calculation for shear mode frequencies using the model of Sotani et al. [26] and the shear modulus of magnetised crusts as described above. We calculate fundamental shear mode frequencies for a neutron star mass of 1.4 M\(_{\odot }\) as well as magnetic fields as high as \(4.414 \times 10^{17}\) G. When we compare those frequencies involving magnetised crust with those of the non-magnetised crust, we do not find any noticeable change between two cases. For SGR 1900+14 having \(B=4\times 10^{14}\) G and a neutron star mass of 1.4 M\(_{\odot }\), we show in the right panel of Fig. 3 that the observed QPO frequencies match nicely with frequencies estimated using our magnetised crust model. Further we observe that the first radial overtones calculated with our magnetised crust model have higher frequencies than those calculated with the non-magnetised crust model. This is in agreement with the prediction that the radial overtones are susceptible to magnetic effects [23].

6 Summary

We have constructed the model of magnetised neutron star crusts and applied it to shear mode oscillations of magnetars. In particular, we highlighted the effects of strongly quantising magnetic fields on the properties of ground state matter of outer and inner crusts in this article. It is noted that compositions and equations of state of neutron star crusts are significantly altered in strong magnetic fields. Consequently, shear modulus of the crust which is sensitive to the compositions of crusts, is enhanced. We have observed that our model of the magnetised crust might explain the observed shear mode frequencies quite well.