Analytical Solutions of Axial Annular Newtonian Flows with Dynamic Wall Slip

Abstract

We consider the cessation of annular Poiseuille and annular Couette flows of a Newtonian fluid, under the assumption that wall slip occurs following a dynamic slip law, i.e., a law involving a slip-relaxation parameter. The relaxation time-dependent term forces the eigenvalue parameter to appear in the boundary conditions and, thus, the resulting spatial problems correspond to Sturm-Liouville problems different from their static-Navier slip counterparts. The orthogonality conditions of the associated eigenfunctions for both flows of interest are derived and analytical closed-form solutions are then obtained. For comparison purposes, the analytical solutions corresponding to the static Navier slip condition, are derived. Comparisons are also made with the plane Poiseuille and Couette flows when the annular gap becomes small. As expected, flow dynamics becomes slower in the presence of wall slip and this effect is accentuated by increasing the slip-relaxation parameter.

1 Introduction

Τhe classical no-slip boundary condition, dictating that fluid particles adjacent to a (fixed or moving) wall stick to it, is violated in many important macroscopic flows of complex and also simple fluids [1, 2] . Let us denote by $u_{w}^{*}$ the slip velocity, defined as the relative velocity of the fluid particles with respect to that of the wall. Wall slip reduces the required pressure drop and finds application in microfluidics [3]. However, it also has undesired effects, causing, for example, instabilities in certain flows of industrial importance [4, 5]. It also affects measurements in viscometric experiments and needs to be taken into account, in order to determine the true rheology of the fluid under study [6]. The mismatch of viscosity data obtained from different rheometers or from the same rheometer using different radii or gaps is often attributed to wall slip. Different techniques are used in order to get correct estimates of the rheological parameters, such as the Mooney method for capillary rheometers [7] and those suggested by Yoshimura and Prud’homme [8] for circular Couette and parallel disk rheometers.

In general, the slip velocity depends not only on the fluid properties and the flow conditions, such as the shear and normal stresses (which include pressure) and the temperature, but also on the physical properties of the wall/fluid interface [1]. Navier’s law [9] assumes that the slip velocity varies linearly the wall shear stress, $\tau_{w}^{*}$, and introduces a single material parameter $\beta^{*}$ that incorporates all other effects:

$$ u_{w}^{*} = \frac{{\tau_{w}^{*} }}{{\beta^{*} }} $$

(1)

The no-slip boundary condition corresponds to the limiting case where $\beta^{*} \to \infty$. The above equation is static, i.e., the slip velocity is independent of the history of the fluid particles. More involved static slip equations have been proposed in the literature, such as the power-law generalization of the Navier law, non-monotonic slip equations, and equations predicting slip above a stress threshold [1].

Of special interest to the present work are dynamic slip equations that apply to time-dependent flows and include a relaxation time $\lambda^{*}$. The dynamic extension of Eq. (1) takes the form

$$ u_{w}^{*} + \lambda^{*} \frac{{\partial u_{w}^{*} }}{{\partial t^{*} }} = \frac{{\tau_{w}^{*} }}{{\beta^{*} }} $$

(2)

where $t^{*}$ is the time. It should be pointed out that in steady-state flows, Eq. (2) is equivalent to the Navier-slip Eq. (1).

Kaoullas and Georgiou [10] used separation of variables to derive analytical solutions for the start-up and cessation of Newtonian plane and axisymmetric Poiseuille and plane a circular Couette flows with dynamic wall slip following Eq. (2). They pointed out that since the eigenvalue parameter also appears in the boundary conditions, the resulting spatial problem corresponds to a Sturm–Liouville problem different from that found using the static Navier law (1). The main observation is that dynamic wall slip damps the flow development even more than static wall slip. The same conclusion was also made by Abou-Dina et al. [11], who obtained equivalent analytical solutions of the start-up Newtonian Couette flow with dynamic wall slip along the fixed wall using separation of variables and also the one-sided Fourier transform methods.

The objective of the present work is to derive analytical solutions of two Newtonian flows in an annular tube with dynamic wall slip: (a) the start-up of annular Poiseuille flow, i.e., the flow caused by imposing a constant pressure-gradient; and (b) the start-up annular Couette flow, i.e., the flow resulting by suddenly moving the inner cylinder in the axial direction. Both flows find industrial applications, e.g., in the oil industry. To the best of our knowledge, the effects of dynamic wall slip on these two flows have not been investigated in the literature.

Fig. 1.

Geometry of annular Poiseuille flow; the flow is driven by a pressure gradient $G^{*} = ( - \partial p^{*} /\partial z^{*} )$.

The analytical solutions of the two flows of interest are derived in Sects. 2 and 3. In Sect. 2, the cessation of annular Poiseuille flow is analysed. The cessation of annular Couette flow is studied in Sect. 3. Results for both flows are presented and discussed in Sect. 4. Concluding remarks are provided in Sect. 5.

2 Annular Poiseuille Flow

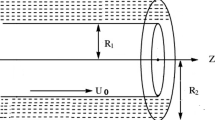
We consider the annular Poiseuille flow, i.e., the pressure-driven flow of a Newtonian fluid in an infinitely long annular tube. Let the radii of the inner and outer cylinders be $\kappa R^{*}$ and $R^{*}$, where $0 < \kappa < 1$, as illustrated in Fig. 1. Using cylindrical coordinates $(r^{*} ,\theta ,z^{*} )$ and assuming that the flow is incompressible and axisymmetric and gravity is negligible, the velocity $u_{z}^{*} = u_{z}^{*} (r^{*} ,t^{*} )$ and the z-component of the momentum equation becomes [12]:

$$ \rho^{*} \frac{{\partial u_{z}^{*} }}{{\partial t^{*} }} = G^{*} + \eta^{*} \frac{1}{{r^{*} }}\frac{\partial \;}{{\partial r^{*} }}\left( {r^{*} \frac{{\partial u_{z}^{*} }}{{\partial r^{*} }}} \right) $$

(3)

where $G^{*} = ( - \partial p^{*} /\partial z^{*} )$ is the pressure gradient, and $\rho^{*}$ and $\eta^{*}$ are respectively the fluid density and viscosity, both of which are constant.

In the present work, we assume that dynamic wall slip occurs along the two cylinders, i.e., at $r^{*} = \kappa R^{*}$ and $r^{*} = R^{*}$, and denote the corresponding slip velocities by $u_{w1}^{*}$ and $u_{w2}^{*}$:

$$ \left. {\begin{array}{*{20}c} {u_{z}^{*} (\kappa R^{*} ,t^{*} ) = u_{w1}^{*} (t^{*} )} \\ {u_{z}^{*} (R^{*} ,t^{*} ) = u_{w2}^{*} (t^{*} )} \\ \end{array} } \right\} $$

(4)

Slip obeys the dynamic-slip law in Eq. (2), where

$$ \tau_{w}^{*} = \left| {\tau_{rz}^{*} } \right|_{w} = \left| {\eta \frac{{\partial u_{z}^{*} }}{{\partial r^{*} }}} \right|_{w} $$

(5)

Given that the velocity near the two cylinders is smaller than in the core of the annulus, the velocity derivative is positive near the inner cylinder and negative near the outer cylinder. Therefore, applying the dynamic-slip law we obtain the following boundary conditions:

$$ \left. {\begin{array}{*{20}c} {u_{z}^{*} (\kappa R^{*} ,t^{*} ) + \lambda^{*} \frac{{\partial u_{z}^{*} (\kappa R^{*} ,t^{*} )}}{{\partial t^{*} }} = \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{\partial u_{z}^{*} (\kappa R^{*} ,t^{*} )}}{{\partial r^{*} }}} \\ {u_{z}^{*} (R^{*} ,t^{*} ) + \lambda^{*} \frac{{\partial u_{z}^{*} (R^{*} ,t^{*} )}}{{\partial t^{*} }} = - \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{\partial u_{z}^{*} (R^{*} ,t^{*} )}}{{\partial r^{*} }}} \\ \end{array} } \right\} $$

(6)

2.1 Steady-State Solution

Let us denote by $\overline{u}_{z}^{*} = \overline{u}_{z}^{*} (r^{*} )$ the steady-state velocity. Combining the simplified Eqs. (3) and (6), one obtains the following boundary value problem:

$$ \left. {\begin{array}{*{20}c} \begin{gathered} \frac{d\;}{{dr^{*} }}\left( {r^{*} \frac{{d\overline{u}_{z}^{*} }}{{dr^{*} }}} \right) = - \frac{{G^{*} r^{*} }}{{\eta^{*} }} \hfill \\ \overline{u}_{z}^{*} (\kappa R^{*} ,t^{*} ) = \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{d\overline{u}_{z}^{*} (\kappa R^{*} ,t^{*} )}}{{dr^{*} }} \hfill \\ \end{gathered} \\ {\overline{u}_{z}^{*} (R^{*} ,t^{*} ) = - \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{d\overline{u}_{z}^{*} (R^{*} ,t^{*} )}}{{dr^{*} }}} \\ \end{array} } \right\} $$

(7)

It is straightforward to integrate and apply the boundary conditions [13]. One then obtains the following solution:

$$ \overline{u}_{z}^{*} (r^{*} ) = \frac{{G^{*} R^{*2} }}{{4\eta^{*} }}\left[ {1 + 2\left( {1 - \sigma^{2} } \right)B - \frac{{r^{*2} }}{{R^{*2} }} - 2\sigma^{2} \ln \frac{{R^{*} }}{{r^{*} }}} \right] $$

(8)

where

$$ B \equiv \frac{{\eta^{*} }}{{\beta^{*} R^{*} }} $$

(9)

is the dimensionless slip number and

$$ \sigma^{2} = \frac{{1 - \kappa^{2} + 2(1 + \kappa )B}}{{2\left[ {\ln (1/\kappa ) + (1 + 1/\kappa )B} \right]}} $$

(10)

It should be noted that $r_{M}^{*} = \sigma R^{*}$ is the radius at which the steady-state velocity is maximum. The two slip velocities are also easily calculated:

$$ \overline{u}_{w1}^{*} = \frac{{G^{*} R^{*2} B}}{{2\kappa \eta^{*} }}\left( {\sigma^{2} - \kappa^{2} } \right) $$

(11)

and

$$ \overline{u}_{w2}^{*} = \frac{{G^{*} R^{*2} B}}{{2\eta^{*} }}\left( {1 - \sigma^{2} } \right) $$

(12)

For the steady-state volumetric flow rate $\overline{Q}^{*} = 2\pi \int_{0}^{{R^{*} }} {\overline{u}_{z}^{*} } (r^{*} )r^{*} dr^{*}$, one gets

$$ \overline{Q}^{*} = \frac{{\pi G^{*} R^{*4} }}{{8\eta^{*} }}\left\{ {1 - \kappa^{4} + 4\left( {1 + \kappa^{3} } \right)B - \frac{{\left[ {1 - \kappa^{2} + 2(1 + \kappa )B} \right]^{2} }}{\ln (1/\kappa ) + (1 + 1/\kappa )B}} \right\} $$

(13)

Scaling the velocity $\overline{u}_{z}^{*} (r^{*} )$ by the mean velocity in the annular tube,

$$ \overline{V}^{*} = \frac{{G^{*} R^{*2} }}{{8\eta^{*} \left( {1 - \kappa^{2} } \right)}}\left\{ {1 - \kappa^{4} + 4\left( {1 + \kappa^{3} } \right)B - \frac{{\left[ {1 - \kappa^{2} + 2(1 + \kappa )B} \right]^{2} }}{\ln (1/\kappa ) + (1 + 1/\kappa )B}} \right\} $$

(14)

we obtain the following expression for the dimensionless velocity:

$$ \overline{u}_{z}^{{}} (r) \equiv \frac{{\overline{u}_{z}^{*} (r^{*} )}}{{\overline{V}^{*} }} = \frac{{2\left( {1 - \kappa^{2} } \right)\left[ {1 + 2\left( {1 - \sigma^{2} } \right)B - r^{2} - 2\sigma^{2} \ln \frac{1}{r}} \right]}}{{1 - \kappa^{4} + 4\left( {1 + \kappa^{3} } \right)B - \frac{{\left[ {1 - \kappa^{2} + 2(1 + \kappa )B} \right]^{2} }}{\ln (1/\kappa ) + (1 + 1/\kappa )B}}} $$

(15)

where $r = r^{*} /R^{*}$. The no-slip solution is recovered by setting $B = 0$. The dimensionless slip velocities are given by

$$ \overline{u}_{w1}^{{}} = \frac{{4\left( {1 - \kappa^{2} } \right)\left( {\sigma^{2} - \kappa^{2} } \right)B}}{{\kappa \left\{ {1 - \kappa^{4} + 4\left( {1 + \kappa^{3} } \right)B - \frac{{\left[ {1 - \kappa^{2} + 2(1 + \kappa )B} \right]^{2} }}{\ln (1/\kappa ) + (1 + 1/\kappa )B}} \right\}}},\quad \overline{u}_{w2}^{{}} = \kappa \overline{u}_{w1}^{{}} $$

(16)

2.2 Cessation Flow

We consider now the cessation flow, assuming that initially ($t^{*} = 0$) the velocity is the steady-state solution in Eq. (15) and that the pressure gradient suddenly ($t^{*} > 0$) vanishes. We work with dimensionless equations scaling $r^{*}$ by $R^{*}$, $u_{z}^{*}$ by the mean steady-state velocity $\overline{V}^{*}$, and the time $t^{*}$ by $\rho^{*} R^{*2} /\eta^{*}$. The resulting initial boundary value problem can be written as follows:

$$ \left. {\begin{array}{*{20}c} \begin{gathered} \frac{{\partial u_{z} }}{\partial t} = \frac{1}{r}\frac{\partial \;}{{\partial r}}\left( {r\frac{{\partial u_{z} }}{\partial r}} \right),\quad \kappa \le r \le 1,\quad t \ge 0 \hfill \\ u_{z} (\kappa ,t) + \Lambda \frac{{\partial u_{z} (\kappa ,t)}}{\partial t} = B\frac{{\partial u_{z} (\kappa ,t)}}{\partial r},\quad t \ge 0 \hfill \\ \end{gathered} \\ \begin{gathered} u_{z} (1,t) + \Lambda \frac{{\partial u_{z} (1,t)}}{\partial t} = - B\frac{{\partial u_{z} (1,t)}}{\partial r},\quad t \ge 0 \hfill \\ u_{z} (r,0) = \overline{u}_{z} (r),\quad \kappa \le r \le 1 \hfill \\ \end{gathered} \\ \end{array} } \right\} $$

(17)

where

$$ \Lambda \equiv \frac{{\lambda^{*} \eta^{*} }}{{\rho^{*} R^{*2} }} $$

(18)

is the dimensionless slip relaxation number. To solve problem (17) we use the method of separation of variables. The following expression is obtained for the velocity:

$$ u_{z} (r,t) = \sum\limits_{n = 1}^{\infty } {A_{n} } Z_{0}^{(n)} (\alpha_{n} r)e^{{ - \alpha_{n}^{2} t}} $$

(19)

where $Z_{i}^{(n)} (x) \equiv J_{i} (x) + \beta_{n} Y_{i} (x),\quad i = 0,1$, and $J_{i} (x)$ and $Y_{i} (x)$ are the ith-otder Bessel functions of the first and second kind, respectively, and $(\alpha_{n} ,\beta_{n} )$ are the nth solution of the system:

$$ \left. {\begin{array}{*{20}c} {Z_{0}^{(n)} (\kappa \alpha_{n} )\left( {1 - \Lambda \alpha_{n}^{2} } \right) = - B\alpha_{n} Z_{1}^{(n)} (\kappa \alpha_{n} )} \\ {Z_{0}^{(n)} (\alpha_{n} )\left( {1 - \Lambda \alpha_{n}^{2} } \right) = B\alpha_{n} Z_{1}^{(n)} (\alpha_{n} ) \, } \\ \end{array} } \right\} $$

(20)

The constants $A_{n}$ are determined upon application of the initial condition in Eq. (17) and the proper orthogonality condition:

$$ \begin{aligned} A_{n} &= \frac{{4\left( {1 - \kappa^{2} } \right)\left( {1 - \Lambda \alpha_{n}^{2} } \right)}}{{B\alpha_{n}^{2} \left[ {(B + 2\Lambda )Z_{1}^{(n)2} (\alpha_{n} ) + \kappa (2\Lambda - \kappa B)Z_{1}^{(n)2} (\kappa \alpha_{n} )} \right] + \left( {1 - \Lambda \alpha_{n}^{2} } \right)^{2} \left[ {Z_{1}^{(n)2} (\alpha_{n} ) - \kappa^{2} Z_{1}^{(n)2} (\kappa \alpha_{n} )} \right]}} \hfill \\& \times \frac{{\left\{ \begin{gathered} \Lambda \alpha_{n}^{4} \left[ {2B(1 - \sigma^{2} )Z_{1}^{(n)} (\alpha_{n} ) - \kappa \left( {2B(1 - \sigma^{2} ) + 1 - \kappa^{2} - 2\sigma^{2} \ln (1/\kappa )} \right)Z_{1}^{(n)} (\kappa \alpha_{n} )} \right] \hfill \\ \, + 2\left( {1 - \Lambda \alpha_{n}^{2} } \right)\left[ {2 + B(1 - \sigma^{2} )\alpha_{n}^{2} } \right]\left[ {Z_{1}^{(n)} (\alpha_{n} ) - \kappa Z_{1}^{(n)} (\kappa \alpha_{n} )} \right] \hfill \\ \, - 2B\alpha_{n}^{2} \left[ {(1 - \sigma^{2} )Z_{1}^{(n)} (\alpha_{n} ) - (\sigma^{2} - \kappa^{2} )Z_{1}^{(n)} (\kappa \alpha_{n} )} \right] \hfill \\ \end{gathered} \right\}}}{{\alpha_{n}^{3} \left\{ {1 - \kappa^{4} + 4\left( {1 + \kappa^{3} } \right)B - \frac{{\left[ {1 - \kappa^{2} + (1 + \kappa )B} \right]^{2} }}{\ln (1/\kappa ) + (1 + 1/\kappa )B}} \right\}}} \hfill \\ \end{aligned} $$

(21)

The two slip velocities are simply given by:

$$ u_{w1} (t) = u_{z} (\kappa ,t) = \sum\limits_{n = 1}^{\infty } {A_{n} } Z_{0}^{(n)} (\kappa \alpha_{n} )e^{{ - \alpha_{n}^{2} t}} $$

(22)

and

$$ u_{w2} (t) = u_{z} (1,t) = \sum\limits_{n = 1}^{\infty } {A_{n} } Z_{0}^{(n)} (\alpha_{n} )e^{{ - \alpha_{n}^{2} t}} $$

(23)

Also, the volumetric flow rate is

$$ Q(t) = \sum\limits_{n = 1}^{\infty } {\frac{{A_{n} }}{{\alpha_{n} }}} \left[ {Z_{1}^{(n)} (\alpha_{n} ) - \kappa Z_{1}^{(n)} (\kappa \alpha_{n} )} \right]e^{{ - \alpha_{n}^{2} t}} $$

(24)

Fig. 2.

Geometry of annular Couette flow; the flow is driven by the motion of the inner cylinder.

3 Annular Couette Flow

In this section, the annular Couette flow is considered, i.e., the flow between two coaxial cylinders of infinite length and radii $\kappa R^{*}$ and $R^{*}$, which is driven by the axial motion of the inner cylinder.

3.1 Steady-State Solution

We first consider the steady-state flow in which the inner cylinder moves at a constant speed $V^{*}$, as illustrated in Fig. 2. Given that the pressure gradient is zero, integrating the steady-state version of Eq. (3) gives $\overline{u}_{z}^{ * } \left( {r^{*} } \right) = c_{1}^{*} \ln r^{*} + c_{2}^{*}$, where the constants $c_{1}^{*}$ and $c_{2}^{*}$ are determined from the boundary conditions:

$$ \left. {\begin{array}{*{20}c} {u_{z}^{ * } (\kappa R^{*} ) = V^{*} - u_{w1}^{*} } \\ {u_{z}^{ * } (R^{*} ) = u_{w2}^{*} } \\ \end{array} } \right\} $$

(25)

Since the velocity is a decreasing function of the radial distance, the shear stress $\tau_{rz}^{ * } = \eta^{*} du_{z}^{*} /dr^{*}$ is negative everywhere in the flow domain, and thus Eq. (25) takes the form:

$$ \left. {\begin{array}{*{20}c} {u_{z}^{ * } (\kappa R^{*} ) = V^{*} + \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{du_{z}^{ * } (\kappa R^{*} )}}{{dr^{*} }}} \\ {u_{z}^{ * } (R^{*} ) = - \frac{{\eta^{*} }}{{\beta^{*} }}\frac{{du_{z}^{ * } (R^{*} )}}{{dr^{*} }}} \\ \end{array} } \right\} $$

(26)

where the static version of Eq. (2), i.e., Navier slip, has been employed. It is straightforward to show that the steady-state velocity is given by

$$ \overline{u}_{z}^{*} (r^{*} ) = \frac{{B + \ln (R^{*} /r^{*} )}}{(1 + 1/k)B + \ln (1/\kappa )}V^{*} $$

(27)

The volumetric flow rate is found to be

$$ Q^{*} = \frac{{\pi \left( {1 - \kappa^{2} } \right)R^{*2} V^{*} \left[ {1 + 2B - 2\ln (1/\kappa )/(1/\kappa^{2} - 1)} \right]}}{{2\left[ {(1 + 1/k)B + \ln (1/\kappa )} \right]}} $$

(28)

3.2 Cessation Flow

We consider the cessation flow, i.e., we assume that at $t^{*} = 0$ the velocity is given by Eq. (27), i.e., the steady-state solution, and suddenly the inner cylinder stops moving. We work with dimensionless equations scaling lengths and time as in Sect. 2 and the velocity $u_{z}^{*}$ by the initial speed $V^{*}$ of the inner cylinder. The resulting initial boundary value problem is identical to that in Eq. (17). Therefore, the velocity is given by Eq. (25), where $(\alpha_{n} ,\beta_{n} )$ are the nth positive solution of Eq. (20) and the constants $A_{n}$ are found by applying the initial condition

$$ u_{z} (r,0) = \overline{u}_{z} (r) = \frac{B + \ln (1/r)}{{(1 + 1/k)B + \ln (1/\kappa )}} $$

(29)

Using the proper orthogonality condition, one finds that

$$ A_{n} = - \frac{{2\kappa \left( {1 - \Lambda \alpha_{n}^{2} } \right)Z_{1}^{\left( n \right)} \left( {\kappa \alpha_{n} } \right)/\alpha_{n} }}{{\left\{ \begin{array}{r} B\alpha_{n}^{2} \left[ {(B + 2\Lambda )Z_{1}^{(n)2} (\alpha_{n} ) + \kappa (2\Lambda - \kappa B)Z_{1}^{(n)2} (\kappa \alpha_{n} )} \right] \hfill \\ + \left( {1 - \Lambda \alpha_{n}^{2} } \right)^{2} \left[ {Z_{1}^{(n)2} (\alpha_{n} ) - \kappa^{2} Z_{1}^{(n)2} (\kappa \alpha_{n} )} \right] \hfill \\ \end{array} \right\}}} $$

(30)

It should be noted that the two slip velocities and the volumetric flow rate are given by Eqs. (22)–(24).

Fig. 3.

Evolution of the dimensionless velocity in cessation of annular Poiseuille flow with dynamic wall slip when $B = 0.1$ (moderate slip) and $\kappa = 0.5$: (a) $\Lambda = 0$ (Navier slip; $t = 0$, 0.01, 0.02, 0.05, 0.1, 0.2); (b) $\Lambda = 0.02$ ($t = 0$, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2); (c) $\Lambda = 0.05$ ($t = 0$, 0.01, 0.02, 0.05, 0.1, 0.2, 0.4). The red profile is the initial steady-state solution.

Fig. 4.

Evolution of the dimensionless velocity in cessation of annular Poiseuille flow with dynamic wall slip when $B = 1$ (strong slip) and $\kappa = 0.5$: (a) $\Lambda = 0$ (Navier slip; $t = 0$, 0.05, 0.1, 0.2, 0.4, 0.8); (b) $\Lambda = 0.02$ ($t = 0$, 0.05, 0.1, 0.2, 0.4, 0.8); (c) $\Lambda = 0.05$ ($t = 0$, 0.05, 0.1, 0.2, 0.4, 0.8). The red profile is the initial steady-state solution.

Fig. 5.

Evolution of the dimensionless volumetric flow rate in cessation of annular Poiseuille flow with dynamic wall slip when $\kappa = 0.5$ and $\Lambda = 0$ (Navier slip), 0.01 and 0.02: (a) $B = 0.01$ (weak slip); (b) $B = 0.1$ (moderate slip); (c) $B = 1$ (strong slip). The red dashed line corresponds to the no-slip case.

4 Results and Discussion

Results have been obtained for various values of the radii ratio $\kappa$ and wide ranges of the slip parameters $B$ and $\Lambda$. The Fourier modes, i.e., the solutions of the system in Eq. (20) are easily determined using standard methods, marching along the positive x-axis calculating all the roots till the desired number $N$ is reached. Our numerical experiments revealed that considering $N = 1000$ terms of the solution in Eq. (19) was sufficient to ensure series convergence. It should be noted that the series was not convergent at very small times (of the order of $10^{ - 6}$) resulting in oscillations, that persist even when much more terms (up to $N = 10^{6}$) are employed. However, at such small times the time-dependent solution does not differ much from the initial steady-state solutions in Eqs. (15) and (27) for the Poiseuille and Couette flows, respectively. Next, results for $\kappa = 0.5$ are presented and discussed.

4.1 Annular Poiseuille Flow

The effect of the relaxation parameter $\Lambda$ on the evolution of the velocity is illustrated in Figs. 3 and 4, where results for $B = 0.1$ (moderate slip) and 1 (strong slip) are shown. Note that the top plots correspond to $\Lambda = 0$, i.e., to (static) Navier slip. In agreement with the literature [10, 11], the evolution of the velocity becomes slower as the value of $\Lambda$ is increased. When slip is strong, which is the case in Fig. 4, the velocity profiles become rather flat and cessation is much slower and the effect of $\Lambda$ is not so pronounced. In other words, dynamic wall slip is not important when slip is very strong.

The combined effects of the slip and relaxation numbers on the evolution of the flow are also illustrated in Fig. 5, where the calculated volumetric flow rates for different values of the two parameters are plotted. One observes that the evolution of $Q(t)$ becomes slower when $B$ or $\Lambda$ are increased and that the effect of $\Lambda$ is more pronounced when slip is weak (Fig. 5a) or moderate (Fig. 5b).

4.2 Annular Couette Flow

The evolution of the velocity in the case of no or static wall slip is illustrated in Fig. 6, where results for $\Lambda = 0$ and $B = 0$, 0.1 and 1 are shown. As expected, the initial steady-state velocity profile tends to become flat and cessation is damped as wall slip becomes stronger. It is also clear that initially only the flow adjacent the inner cylinder of the annulus is affected. The inner slip velocity $u_{w1}$ is initially much bigger than $u_{w2} .$ As the phenomenon is developed the difference between the two slip velocities diminishes, as they both tend to zero, and the velocity distribution tends to become flatter and symmetric.

Fig. 6.

Evolution of the dimensionless velocity in cessation of annular Couette flow with Navier slip when $\kappa = 0.5$: (a) $B = 0$ (no slip; $t = 0$, 0.0005, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1); (b) $B = 0.1$ (moderate slip; same times as in (a)); (c) $B = 1$ (strong slip; $t = 0$, 0.001, 0.01, 0.1, 0.2, 0.4, 0.8). The red profile is the initial steady-state solution.

Fig. 7.

Evolution of the dimensionless velocity in cessation of annular Couette flow with dynamic wall slip when $\kappa = 0.5$ and $B = 0.1$: (a) $\Lambda = 0$ (Navier slip; $t = 0$, 0.0005, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1); (b) $\Lambda = 0.02$ ($t = 0$, 0.0001, 0.0005, 0.001, 0.002, 0.005, 0.01, 0.02, 0.05, 0.1); (c) $B = 1$ (same times as in (b)). The red profile is the initial steady-state solution.

Fig. 8.

Evolution of the two slip velocities $u_{w1}$ (solid blue) $u_{w2}$ (dashed red) in cessation of annular Couette flow when $\kappa = 0.5$ and $B = 0.1$: (a) $\Lambda = 0$ (Navier slip); (b) $\Lambda = 0.02$; (c) $\Lambda = 0.05$.

Fig. 9.

Evolution of the dimensionless volumetric flow rate in cessation of annular Poiseuille flow with dynamic wall slip when $\kappa = 0.5$ and $\Lambda = 0$ (Navier slip), 0.005 and 0.01: (a) $B = 0.01$ (weak slip); (b) $B = 0.1$ (moderate slip); (c) $B = 1$ (strong slip). The red dashed line corresponds to the no-slip case.

The effect of the relaxation parameter is illustrated in Fig. 7, where results for $B = 0.1$ (moderate slip) and different values of $\Lambda$ are shown. Again, cessation is slowed down and the velocity distribution tends to become flat near the inner cylinder. The evolution of the two slip velocities in the three cases of Fig. 7 is shown in Fig. 8. The combined effects of $B$ and $\Lambda$ on the volumetric flow rate are shown in Fig. 9. The role of the relaxation parameter is important only when slip is weak or moderate.

5 Conclusions

We used separation of variables to derive analytical solutions for the cessation of annular Poiseuille and Couette flows of a Newtonian fluid exhibiting dynamic wall slip. It has been demonstrated that, under the assumption that the same slip law applies along both cylinders of the annulus, the two solutions share the same Fourier modes, the only difference being in the initial condition. Representative results for a radii ratio $\kappa = 0.5$ have been presented showing that cessation is damped by the slip and relaxation parameters, in agreement with previous studies in the literature for other flows [10, 11]. It has also been demonstrated that the effect of the slip relaxation parameter is not significant when slip is strong.