A Cooperative Game Approach for Solving Water Resources Allocation Problem

Abstract

In water resources allocation problem, different stakeholders are faced with conflicting objectives and an optimal allocation of shared water resources in water transfer projects became an important task, taking into account the utilities of the different stakeholders. In Iran, there is unevenly distribution of water resources as well as increasing water demands, which have brought a need to transfer water from the Karoon river basin to the Rafsanjan basin in central Iran. Therefore, cooperative game theory can be used to analyze these problems, taking the advantage of cooperative games in maximizing the total net benefit of the shared stakeholders as well as increasing the individual shares of the allocated water to each stakeholder. In this paper, two cooperative game models are developed for modeling efficient water allocation among water stakeholders in water allocation problems in southern Iran. The main objective is to reallocate the water resources to achieve an equitable way of distributing these benefits among the water stakeholders to let them have the economic incentives for cooperation. Depending on the type of cooperation and the nature of the payoffs values, a fuzzy and a stochastic cooperative models are presented. The results showed that the models are appropriate in modeling real-world uncertain problems and efficient in allocating benefits specifically when considering the stochastic nature for payoffs.

1 Introduction

In water allocation problems, there are usually several stakeholders with different and conflicting objectives. These conflicts arise when several water users compete for a limited amount of water supply. To achieve equitable and efficient water allocation, this requires the cooperation of all stakeholders in sharing water resources. Thus, water allocation methodologies need to be established to maintain equitable and efficient water allocations at river basins level. Cooperative game theory was used to model this scenario of water resource allocation, taking the advantage of cooperative games in maximizing the total net benefit of the shared stakeholders as well as increasing the individual shares of the allocated water to each stakeholder.

The aim of this paper is developing two cooperative game models for water resources reallocation to achieve an equitable way of distributing these benefits among the water stakeholders to let them have the economic incentives for cooperation. Depending on the type of cooperation and the nature of the payoffs values, a fuzzy and a stochastic cooperative models are presented. These models are used to solve a case study of water allocation problem in Southern Iran, showing the higher benefits achieved from the cooperation of the water stakeholders.

The organization of this paper is as follows: Sect. 2 presents the related work for solving water resources allocation problems. Section 3 presents the fuzzy and stochastic cooperative models, respectively and the framework for these models. Implementation for these models on a real case study in Iran is carried out in Sect. 4. Sections 5 gives the main concluding remarks.

2 Related Work

“Several attempts in the literature have been done for studying water resources allocation problem. Kucukmehmetoglu (2009) established a methodology to measure the rational economic and political impacts of extensive reservoir projects throughout a basin, using both linear programming for calculating benefits of coalitions, and game theory concepts (core and Shapley value) for evaluating the impacts of reservoirs. Sadegh et al. (2010) and Sadegh and Kerachian (2011) developed a methodology based on crisp and fuzzy Shapley games for optimal allocation of interbasin water resources. In their methodology, some fuzzy coalitions were constituted, and the total net benefit of the system was reallocated to water users using fuzzy Shapley value game with crisp payoffs.

Mahjouri and Ardestani (2010) developed a new game theoretic methodology for interbasin water transfer management to supply the competing users in a fair way, while the efficiency and environmental sustainability criteria were satisfied and the utilities of water users were incorporated. Mahjouri and Ardestani (2011) developed two cooperative and non-cooperative methodologies for a large-scale water allocation problem in Southern Iran. The water shares of the water users and their net benefits were determined using optimization models having economic objectives with respect to the physical and environmental constraints of the system.

Sadegh and Kerachian (2011) developed two new solution concepts for fuzzy cooperative games with crisp characteristic functions, namely Fuzzy Least Core and Fuzzy Weak Least Core. They aimed for optimal allocation of available water resources and associated benefits to water users in a river basin. Review of the previous works shows that the applicability and efficiency of cooperative games with fuzzy characteristic functions and fuzzy coalitions in modeling water resource allocation problems have not been yet investigated. Nikoo et al. (2012) developed a new methodology based on interval optimization and game theory for optimal operation of an interbasin water transfer system considering efficiency, equity and sustainability criteria. They proposed a linear version of the agricultural water production function and used it for incorporating deficit irrigation.”

3 Proposed Models

In this section, two game models are proposed. Depending on the type of cooperation between water stakeholders whether partial or full cooperation, and the type of payoffs values whether fuzzy or stochastic random variables, a fuzzy or stochastic cooperative game models is determined. In the following, the details of developing both models are explained.

3.1 A Fuzzy Cooperative Game Model

In the fuzzy game model, water users could participate in forming the fuzzy grand coalition with a different participation rates, and therefore, they need not to use all of their initial water shares in the grand coalition. Also, handling the nature of the payoffs values as fuzzy numbers with known membership functions. A closed form formula in this model is developed that optimally allocates the payoffs among the cooperating players.

Taking imprecision of information in decision-making problems into account, a fuzzy characteristic function (i.e., fuzzy coalition value) can be incorporated into a cooperative game, represented by fuzzy numbers ω. Therefore, the characteristic function of such a game associates a crisp coalition with a fuzzy number ω(S). Assessing such fuzzy numbers for any crisp coalition S, a cooperative game with crisp coalitions and fuzzy characteristic function is defined by a pair (N, ω), where the fuzzy characteristic function ω: P(N) → ${\mathfrak{R}}^{+}=\{\tilde{r }\in \mathfrak{R}|\tilde{r }\ge 0\}$ is such that ω(φ) = 0, (where $\mathfrak{R}$ is the fuzzy real line).

A fuzzy cooperative game (FCGame), i.e., with fuzzy coalitions and fuzzy characteristic function, is a pair (N, $\stackrel{\sim }{\omega }$) where N is the set of players with i ϵ N = {1, …, n} and the fuzzy characteristic function $\stackrel{\sim }{\omega }$: $U$ → $\mathfrak{R}$ for all $U$ $\subseteq$ N, such that ω(φ) = 0. A fuzzy coalition $U$ is a fuzzy subset of N, which is a vector $U$ = {$U$ (1),…, $U$ (n)} with coordinates $U$ (i) contained in the interval [0,1]. The number $U$ (i) indicates the membership grade of i in $U$. The class of all fuzzy subsets of $U$ is denoted by F(N). For a fuzzy subset $U$, , the α–level set is defined as: [$U$]_α = {i ϵ N | $U$ (i) ≥ α}, and the support set is denoted by supp($U$) = {i ϵ N | $U$ (i) > 0} (Borkotokey 2008).

Let x($U$) = (x₁($U$), …, x_n($U$)) be the payoff vector, such that x_i($U$) is the payoff of player i of the fuzzy coalition $U$ ϵ F(N). Since all players of coalition U cooperate together to maximize their profit, a linear multi-objective programming model can be formulated for any fuzzy coalition $U$ ϵ F(N) as follows (Tharwat et al. 2011):

Max (${w}_{1}{x}_{1}(U)$, ${w}_{2}{x}_{2}(U)$, …, ${w}_{n}{x}_{n}(U)$)

Subject to

$$ \begin{array}{*{20}l} { \sum \limits_{i \in {\text{Supp}}(U)} x_i ({\text{U}}) = \tilde{\omega }(U),} \hfill & {i{ } = { }1,{ } \ldots ,{ }n} \hfill \\ {x_i (U) \ge [U(i) \cdot \tilde{\omega }(\{ {\text{i}}\} )],} \hfill & {\forall i \in {\text{supp}}(U)} \hfill \\ {x_i (U) = 0,} \hfill & {\forall i \notin {\text{supp}}(U)} \hfill \\ \end{array} $$

(1)

where ${w}_{i}=\left[\stackrel{\sim }{\omega }\left({\text{U}}\right)-\stackrel{\sim }{\omega }\left({\text{U}}-\left\{i\right\}\right)\right]/\stackrel{\sim }{\omega }(U)$.

From the above formulated model, a closed form formula is derived which directly solves fuzzy cooperative games as follows (Sabry et al. 2017):

$$ \begin{aligned} x_i & = U\left( i \right)EV_i + \frac{{EV^{\prime}_U [EV^{\prime}_U - EV^{\prime}_{U - i} ]}}{{\sum_{i = 1}^N [EV^{\prime}_U - EV^{\prime}_{U - i} ]}} \\ & = U\left( i \right)EV_i + \frac{{ [EV^{\prime}_U - EV^{\prime}_{U - i} ]}}{{2EV^{\prime}_U \sum_{i = 1}^N EV^{\prime}_{U - i} }} \\ \end{aligned} $$

(2)

where ${EV}_{U}=\frac{{E}_{1}^{U}+ {E}_{2}^{U}}{2}$ is the expected value for the fuzzy worth $\stackrel{\sim }{\omega }$(U).

The developed closed form formula efficiently calculates the payoff distribution among the coalition players through transforming the payoff value of player i and the expected value of the fuzzy worth.

Proposition 1

The payoffs of players obtained by solving the derived formula satisfy both the individual and the group rationality.

Proposition 2

Zero player (Null player) receives zero gain.

3.2 A Stochastic Cooperative Game Model

In stochastic cooperative games, the payoff values are often estimations or approximations of reality. Under a stochastic environment, the value of the grand coalition, i.e., the total profit (or cost) is not given explicitly; rather it is represented as random variable knowing only its probability distribution.

This section presents a stochastic multi-objective optimization model that is developed to deal with stochastic cooperative games. Our research work handled the uncertainties through stochastic payoff functions through the presence of some random variables $\stackrel{\sim }{\nu }(s)$ with known distribution functions, ${F}_{\tilde{v }\left(s\right)}\left(x\right)=P\left\{\stackrel{\sim }{\nu }\left(s\right)\le x\right\}$. Under stochastic cooperative game (SCG), a pair of sets SCG = (I, $\stackrel{\sim }{\nu }$) is used, where I = {1…n}: the set of players; $\stackrel{\sim }{\nu }$(S): incomes (worth) of coalitions S ⊂ I, that are random variables with determined density functions ${P}_{\tilde{v }\left(s\right)}\left(x\right)$ (Suijs et al. 1999; Ma et al. 2008). Thus, a multi-objective chance constrained programming model can be formulated for any coalition with stochastic worth as follows (Tharwat et al. 2019):

$$ \begin{aligned} & {\text{Max}}\quad x_1 \left( \alpha \right),x_2 \left( \alpha \right), \ldots ,x_n \left( \alpha \right) \\ & {\text{Subject to}} \\ & \quad \quad \frac{3B_i }{{3 - B_i^2 }}{\text{e}}^{ - B_{{\text{i}}/2}^2 } \ge \sqrt {{\frac{\pi }{2}}} \left( {2y_i + 1} \right),\quad i = 1, \ldots ,I \\ & \quad \quad \frac{3\delta }{{3 - \delta^2 }}{\text{e}}^{ - \frac{\delta^2 }{2}} \ge \sqrt {{\frac{\pi }{2}}} \left( {2z + 1} \right) \\ & \quad \quad x_i \left( \alpha \right) - B_i \sigma \left[ {\tilde{v}\left( {\text{i}} \right)} \right] \ge E\left[ {\tilde{v}\left( {\text{i}} \right)} \right],\quad i = 1, \ldots ,I \\ & \quad \quad \mathop \sum \limits_{i = 1}^I x_i \left( \alpha \right) - \delta \sigma \left[ {\tilde{v}\left( I \right)} \right] \le E\left[ {\tilde{v}\left( I \right)} \right] \\ & \quad \quad y_i \ge 1 - \alpha , \quad i = 1, \ldots ,I \\ & \quad \quad z \le \alpha \\ & \quad \quad x_i \left( \alpha \right) \ge 0, \quad i = 1, \ldots ,I \\ & \quad \quad B_i ,\delta \quad {\text{are unrestricted in sign}} \\ & \quad \quad 0 \le y_i ,\;z \le 1 \\ \end{aligned} $$

(3)

where $E\left[\tilde{v }\left(i\right)\right]$, $\sigma \left[\tilde{v }\left(i\right)\right]$ and $E\left[\tilde{v }\left(I\right)\right]$, $\sigma \left[\tilde{v }\left(I\right)\right]$ are the mean and standard deviation of the normal random variables $\tilde{v }\left(i\right)$ and $\tilde{v }\left(I\right)$, respectively. ${B}_{i}$ and $\delta$ are the inverse cumulative distribution function of the standard normal random variable $\tilde{v }\left(i\right)$ at ${y}_{i}$ and $\tilde{v }\left(I\right)$ at $z$, respectively.

Proposition 1

Efficiency: The payoff vector of the model provides efficiency as the total payoff of the grand coalition is distributed to all cooperating players.

Proposition 2

Fairness: The payoff vector provides fairness among all cooperating players as it allocates higher share to the player whose individual contribution is higher than another.

Proposition 3

Existence and Uniqueness: The solution of the developed stochastic multi-objective optimization model always exists as the model is converged to the optimal solution based on the derived convergence constraints and provide unique allocation vector.

Proposition 4

Complexity: The number of constraints increases linearly with the number of cooperating players and not exponentially like Shapley value.

3.3 Framework of the Model

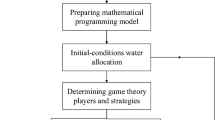
In this section, a general flowchart of the proposed models is illustrated in Fig. 1.

Fig. 1

Framework of the proposed models

4 Case Study

In Iran, there is unevenly distribution of water resources due to precipitation. In central Iran, there is low rate of precipitation and increasing water demands, which have led to high usage on the groundwater resources, which are the only dependable water resources in this region. As such, recently, there is a need to transfer water from the Karoon river basin in southwestern Iran to the Rafsanjan basin in central Iran. Two important rivers are the main branches to the Karoon river basin, the Karoon and Dez. These two rivers connect together and form the huge Karoon river that ends in the Persian Gulf. The Karoon and Dez rivers represent the main sources of water for supplying the agricultural and agro-industrial users.

According to Mahab-Ghods Consulting Engineers (2004), the total water demand and need of the Karoon river basin is 24.9 billion cubic meters while the total discharge (supply) of the great Karoon river is 20.4 billion cubic meters. This statement showed that Karoon river basin had major problems in supplying its own water demands in some months of the year particularly in dry years. One of the most important streams of the great Karoon river is the Solegan river. Its average flow is 26 m³/s. The Iran Water Resources Management Company (IWRMC) had planned to construct Solegan reservoir (dam) on this river to make the opportunity to allocate water to the Rafsanjan plain area in central Iran. The Rafsanjan basin has an annual average precipitation rate of 170 mm, where groundwater resources are the only dependable water resources in this basin, as its rivers are seasonal and their annual discharge are insignificant (shortage is about one million cubic meters) (Fig. 2).

Fig. 2

Solegan reservoir and water demand sectors (Nikoo et al. 2012)

Therefore, IWRMC had decided to supply the water demands of this basin by transferring 250 million cubic meters of water from the Solegan river annually. This transferred amount was used to supply the shortage demands and at the same time protected the groundwater resources in Rafsanjan basins.”

A secondary data was given over a 5-year plan horizon, and the average monthly water demands for the water users were estimated. Table 1 shows the main water demands (players) which are Rafsanjan agricultural sector in the Rafsanjan basin, Khuzestan local agricultural sector in the Karoon basin, Khuzestan modern agro-industrial sector and finally Khuzestan old agro-industrial sector.

Table 1 Main water demands for all users (million m³)

As an initial step, an optimization model was used to determine the initial water allocation shares for all users (players). These allocations are proportional to the shares allocated by the government, which are based on an equity criterion. These are the monthly shares with respect to the legal water supply rights and the reservoir physical and environmental constraints. Because the benefits were calculated yearly, the monthly water allocated shares were converted to the annual ones to be applicable in the calculations of the characteristic functions (Abed Elmdoust and Kerachian 2012). The results of this step were used as inputs to the second step.

4.1 Implementing the Developed Models

The closed form formula for fuzzy cooperative games and the stochastic model developed earlier in Sect. 3 are implemented in this section on the water allocation problem of Southern Iran. A comparison between these implementations are discussed at the end of this section.

4.1.1 A Fuzzy Scenario for Water Allocation

The fuzzy game model allows water users to participate in forming the fuzzy grand coalition with a different participation rates and therefore; they need not to use all of their initial water shares in the grand coalition. In addition, the worth for the formed coalitions is uncertain fuzzy values. The net benefit coefficients and the capacity of each water user, presented in Table 2, are used to calculate the fuzzy worth of each possible crisp coalition. These fuzzy worth of each of the formed crisp coalitions are shown in Table 3.

Table 2 Net benefit coefficient bc(i) and the annual capacity c(i) of users

Table 3 Fuzzy worth of each of the formed crisp coalition

Thus, from the calculated fuzzy worth of coalitions and the participation rates of each user given in Table 4, the total fuzzy worth of the fuzzy grand coalition was determined using the Choquet integral form function for fuzzy games, (Tsurumi et al, 2001) as follows:

$$ \begin{aligned} t\tilde{\omega }\left( {\left\{ {1,2,3,4} \right\}} \right) &= \sum\limits_{m = 1}^{q\left( K \right)} \tilde{\omega }([K]_{r_m } ) \cdot (r_m - r_{m - 1} )\\ & = (102.44,102.53,103.23) \times 10^5 \$ \end{aligned} $$

(4)

Table 4 Participation rate of each water user in the formed fuzzy grand coalition

Solving this fuzzy model with our developed formula for fuzzy games:

Step 1: Defuzzifying the total coalitional worth.

${EV}_{N}$ = 102.68 × ${10}^{5}$$

Step 2: Calculating (${EV}_{N-i}{\prime}$) for all sub-coalitions and ${EV}_{N}{\prime}$

$N-i$	$\left\{\mathrm{2,3},4\right\}$	$\left\{\mathrm{1,3},4\right\}$	$\left\{\mathrm{1,2},4\right\}$	$\left\{\mathrm{1,2},3\right\}$	$\left\{\mathrm{1,2},\mathrm{3,4}\right\}$
$EV$(×${10}^{5}$$)	91.7	95.54	23.75	27.6	102.68
${EV}{\prime}$(×${10}^{5}$$)	59.59	62.9	12.37	0.08	68.13

Step 3: Finding the individual’s profit shares by applying the formula.

Players (i)	1	2	3	4
	Khuzestan modern	Khuzestan old	Khuzestan local	Rafsanjan
(×${10}^{5}$$)	6.2	4.5	50.79	42.39

4.1.2 A Stochastic Scenario for Water Allocation

In the stochastic cooperative game model, water users fully cooperate in the grand coalition with all of their resources, but the coalitional worth in this case is considered normal random variable determined by the net benefit coefficients, ${\varvec{B}}{\varvec{C}}({\varvec{N}})$, and the capacity of each water user, ${\varvec{c}}\left({\varvec{i}},{\varvec{m}}\right)$, shown in Table 5.

Table 5 Stochastic worth for all sub-coalitions of water players

The stochastic worth of each of the formed crisp sub-coalitions were as follows (× ${10}^{5}$$):

Given the four water users will cooperate together sharing all their resources with the stochastic coalitional worth. They want be sure that the total worth is enough to allocate the profit allocation by at least 95%.

Formulating this scenario as stochastic cooperative game, and following our developed model, the obtained deterministic programming problem for the multi-objective stochastic problem will be:

$$ \begin{aligned} & {\text{Max}}\quad 0.4x_1 \left( \alpha \right),{ }0.5x_2 \left( \alpha \right),3.6x_3 \left( \alpha \right),3.1x_4 \left( \alpha \right) \\ & {\text{Subject to}} \\ & \quad \quad x_1 - 0.7\beta_1 \ge 5.2 \\ & \quad \quad x_2 - 0.7\beta_2 \ge 5.6 \\ & \quad \quad x_4 - 0.4\beta_4 \ge 13.5 \\ & \quad \quad \mathop \sum \limits_{i = 1}^4 x_i \left( \alpha \right) - 8.7\delta \le 211 \\ & \quad \quad \frac{3\beta_i }{{3 - \beta_i^2 }} {\text{e}}^{ - \beta_{{\text{i}}/2}^2 } \ge \sqrt {{\frac{\pi }{2}}} \left( {2y_i + 1} \right),\quad i = 1, \ldots ,4 \\ & \quad \quad \frac{3\delta }{{3 - \delta^2 }} {\text{e}}^{ - \frac{\delta^2 }{2}} \ge \sqrt {{\frac{\pi }{2}}} \left( {2z + 1} \right) \\ & \quad \quad y_i \ge 0.95,\quad i = 1, \ldots ,4 \\ & \quad \quad z \le 0.05 \\ & \quad \quad 0 \le y_i ,z \le 1,\;x_i \left( \alpha \right) \ge 0,\quad i = 1, \ldots ,4 \\ & \quad \quad \beta_i ,\delta \quad {\text{are unrestricted in sign}} \\ \end{aligned} $$

4.2 Discussion and Comparison of Results

In the developed closed form fuzzy formula, the profit shares for the water stakeholders are distributed in accordance with the product of the participation rates and the individual worth for each stakeholder. Figure 3 shows the allocation of profit shares for each water user that resulted from applying the developed fuzzy formula.

Fig. 3

Percentages of profit shares distribution with the participation rates using the developed formula

Comparing these obtained values with those obtained using the Hukuhara–Shapley value (Abed Elmdoust and Kerachian 2012):

Players (i)	1	2	3	4
	Khuzestan modern	Khuzestan old	Khuzestan local	Rafsanjan
(×${10}^{5}$$)	6.67	4.52	49.57	40.73

Revealed that the developed formula increased the percentages of the profit shares for stakeholders whose participation rates are higher, which is not the case when solving using the Hukuhara–Shapley Value. Figure 4 shows that the percentages of profit for Khuzestan Local and Rafsanjan were increased to 48.5% and 42.3% respectively using the developed formula against Shapley value that yielded 48.4% and 41.4%, respectively. For Khuzestan Modern and Khuzestan Old, the formula resulted in 5.4% and 3.7% respectively while Shapley value resulted in 6.3 and 3.9%. Thus, the allocation vector resulted from the developed formula reallocated the coalitional worth more efficiently than Hukuhara–Shapley value with less computational effort (no need to calculate crisp Shapley values at the very beginning) and overcoming the Hukuhara conditions.

Fig. 4

Profit shares using the developed formula versus Hukuhara–Shapley value

On the other hand, when solving the water allocation problem using the developed stochastic model, the individual profit shares for the water users will be:

	1 Khuzestan modern	2 Khuzestan old	3 Khuzestan local	4 Rafsanjan
(×${10}^{5}$$)	26.47	35.93	96.93	47.36

1. With total coalitional worth = 206.69 (× ${10}^{5}$$)

When solving the same stochastic model using Shapley value, the allocated payoffs were:

	1 Khuzestan modern	2 Khuzestan old	3 Khuzestan local	4 Rafsanjan
(×${10}^{5}$$)	24.68	31.46	93.68	45.38

1. With total coalitional worth = 195.2 (× ${10}^{5}$$)

Thus, the developed stochastic model allocated 97% of the total coalitional worth, which is more acceptable when compared with Shapley that allocated 92.5% (Fig. 5). Hence, increasing the profit shares for the water users.

Fig. 5

Percentages of profit shares using the developed stochastic model versus Shapley value

Comparisons of results obtained from applying the fuzzy and stochastic game models revealed that applying the stochastic environment and considering the water demands of the water users as stochastic random variables rather than the fuzzy nature for them (as previously considered by other researchers; Abed Elmdoust and Kerachian 2012), achieved efficient and higher profit shares allocations for stakeholders which increased the overall benefit and the individual ones. The major economic benefit achieved when transferring highest water share to Khuzestan local agricultural sector, which resulted in stabilizing and preserving the underground water condition in this area.

5 Conclusions

In this paper, two cooperative game models are developed for modeling efficient water allocation among water stakeholders in water allocation problem. In Southern Iran, there is unevenly distribution of water resources that requires transfer of water resources from basins to another. A fuzzy cooperative game model was developed in which a closed form formula was used to reallocate benefits between water stakeholders. A second scenario of stochastic cooperative game modeling in which the benefits are considered stochastic random variables was used to achieve higher allocations between water stakeholders. The main objective is to reach higher overall net benefit and to achieve an equitable way of distributing these benefits among the water stakeholders that is fair enough to let them have the economic incentives to cooperate forming the grand coalition. The approach for these models consists of two steps. In the first step, an optimization model was used to determine the initial water allocation shares for all users based on an equity criterion. In the second step, water users form coalitions to benefit from cooperation and depending on the nature of payoff values, either the fuzzy or the stochastic model was used to reallocate the benefits in an efficient way. The results showed that the developed fuzzy model is more effective than Hukuhara–Shapley function overcoming its limitation with less computational effort. In addition, applying the developed stochastic model achieved more benefits between water stakeholders than the fuzzy scenario to reach an early assumption that the stochastic nature for the benefits is more realistic than assuming the fuzzy ones. The proposed approach allows applying both fuzzy and stochastic scenarios for solving water allocation problems, though real implementations revealed that considering the stochastic nature for stakeholder payoffs are more beneficial than the fuzzy ones.