Presumably Correct Undersampling

Abstract

This paper presents a data pre-processing algorithm to tackle class imbalance in classification problems by undersampling the majority class. It relies on a formalism termed Presumably Correct Decision Sets aimed at isolating easy (presumably correct) and difficult (presumably incorrect) instances in a classification problem. The former are instances with neighbors that largely share their class label, while the latter have neighbors that mostly belong to a different decision class. The proposed algorithm replaces the presumably correct instances belonging to the majority decision class with prototypes, and it operates under the assumption that removing these instances does not change the boundaries of the decision space. Note that this strategy opposes other methods that remove pairs of instances from different classes that are each other’s closest neighbors. We argue that the training and test data should have similar distribution and complexity and that making the decision classes more separable in the training data would only increase the risks of overfitting. The experiments show that our method improves the generalization capabilities of a baseline classifier, while outperforming other undersampling algorithms reported in the literature.

1 Introduction

Class imbalance is a prevailing challenge in pattern classification, where the distribution of classes is heavily skewed, leading to a scarcity of instances in the minority class relative to the majority class. The class imbalance poses significant difficulties for machine learning algorithms, as they tend to be biased towards the majority class, resulting in suboptimal performance. In real-world scenarios, such as fraud detection or disease diagnosis, where the minority class represents critical instances of interest, accurate prediction becomes crucial. Several techniques have been proposed to address the issue of class imbalance in classification problems by amending the dataset. These techniques can be broadly categorized into undersampling, oversampling, and hybrid approaches.

Undersampling methods aim to reduce the number of instances in the majority class. For example, this can be achieved through random undersampling (RU) [12], where randomly selected instances from the majority class are removed. Alternatively, informed variants of undersampling select instances based on specific criteria or clustering algorithms. For example, Cluster Centroid Undersampling (CCU) [12] utilizes k-means clustering to discover clusters of instances from the majority class and replaces the clusters of majority samples with the cluster centroids. Meanwhile, Edited Nearest Neighbors (ENN) [19] undersamples the majority class by removing samples that are not similar enough to their neighbors. Tomek Links Undersampling (TLU) method [18] identifies pairs of instances from different classes that are close to each other and removes the majority class instances. The Condensed Nearest Neighbor (CoNN) rule [8] is also used in the context of undersampling by iterating over the examples in the majority class and keeping them only if they cannot be classified correctly by the already selected instances. Due to the initial random selection, CoNN method is sensitive to noise. As a solution, One-Sided Selection (OSS) [10] uses Tomek Links to remove noisy instances after applying the CoNN rule. Other undersampling techniques include the NearMiss method [14], which selects majority class instances based on their proximity to minority class instances.

On the other hand, oversampling methods focus on increasing the number of instances in the minority class by replicating or generating synthetic samples [6]. Similar to random undersampling, random oversampling duplicates instances from the minority class randomly. In contrast, synthetic oversampling methods generate synthetic samples with different rules. The most prominent example of synthetic oversampling is the Synthetic Minority Over-sampling Technique (SMOTE) [4]. This method creates new instances by interpolating between the minority class instances and their neighbors. One drawback of SMOTE is that it can generate instances between the inliers and outliers of a class, effectively creating a suboptimal decision space. Several variants of SMOTE try to correct this problem by focusing on samples near the border of the optimal decision function or harder instances from the minority class [7, 9, 11, 16].

Hybrid methods combine both undersampling and oversampling techniques to achieve a balanced dataset. For example, using SMOTE method for oversampling the minority class and then applying an undersampling technique to clean the data is the most common approach. In [2] the authors used Tomek Links, whereas in [1] they propose ENN for the undersampling step. Overall, oversampling methods do not cause data loss, but they are prone to lead to overfitting for the majority of machine learning approaches [3]. Undersampling methods, on the other side, use different heuristics to counteract the data loss from random undersampling. The main advantage of these methods is their ability to reduce the computational complexity of training machine learning models, leading to faster training times and improved efficiency, even when such reduction might not lead to improved algorithms’ performance on the fresh data. For example, the increasingly popular SHAP (SHapley Additive exPlanations) method [13] for generating explanations for machine learning algorithms is one of the methods that benefits from operating with smaller datasets.

In this paper, we tackle the class imbalance problem in machine learning by undersampling the majority class. The proposed method is based on the introduced presumably correct decision sets [15], a set formalism to analyze uncertainty in pattern classification problems. In particular, it focuses on determining which instances are easy (presumably correct) or difficult (presumably incorrect). The former category consists of instances whose neighbors mostly share the same class label, whereas the latter includes instances whose neighbors predominantly belong to a different decision class. The proposed algorithm comprises two main steps. Firstly, we modify the definitions of presumably correct and incorrect instances by using a complete inclusion operator to ensure that all neighbors of presumably correct and incorrect instances are contained in the decision classes being analyzed. Secondly, we cluster the presumably correct instances associated with the majority class into groups and replace them with prototypes. Both steps ensure that the majority class is reduced while preserving the decision boundaries that define the classification problem, translating into reporting the same or improved prediction rates on unseen data.

This paper is organized as follows. Section 2 describes the fundamentals of the presumably correct decision sets, while Sect. 3 presents our method to undersample the majority class in classification problems. Section 4 conducts numerical simulations and performs a comparative analysis between our algorithmic proposal and state-of-the-art undersampling methods. Section 5 provides concluding remarks and some future research avenues.

2 Presumably Correct Decision Sets

Let $P = (X, F \cup {y})$ be a structured classification problem where X is a non-empty finite set of instances, while F is a non-empty finite set of features describing these instances. The decision feature, denoted by $y \notin F$, gives the class label for each instance. For example, if $x \in X$ is associated with the i-th decision class, then we can denote the whole instances as a tuple $(x,y_i)$ where $y_i \in Y$, with Y being the set of possible decision classes. The decision feature induces a partition $X = \{ X_1, \dots , X_i, \dots , X_m \}$ of the universe where $X_i$ contains instances labeled with the i-th decision class, with m being the number of decision classes. Note that this partition satisfies the conditions $\cup _i X_i = X$ and $\cap _i X_i = \emptyset$. Moreover, let us assume that $g: X \rightarrow Y$ is the ground-truth function such that $g(x)=y_i$ if and only if $x \in X_i$. This function returns the decision class of the instance as observed in the dataset. Similarly, the neighborhood function $f: X \rightarrow Y$ determines the decision class of an instance given its neighborhood, and several implementations of this function lead to different algorithms. The certainty degree of such assignment is given by a membership function $\mu : X \times Y \rightarrow [0,1]$ where $\mu (x,i)$ denotes the extent to which x belongs to the i-th decision class as determined by the neighborhood function. In the remainder of this paper, we will refer to $\mu (x,i)$ as $\mu _i(x)$ for convenience.

The rationale of this method is as follows. Let us suppose an instance $x \in X_i$ belongs to the i-th decision class. If most of its neighbors also belong to the i-th decision class, then x is categorized as presumably correct. In contrast, if the majority of its neighbors are labeled with the l-th decision class (where $l \ne i$), then x is considered to be presumably incorrect, even when the ground truth indicates that it is labeled with the i-th decision class in the dataset. In this approach, the membership function quantifies the extent to which the instance resembles the instances in its neighborhood.

Equations (1) and (2) portray the presumably correct and incorrect sets, respectively, associated with the i-th decision class,

$$\begin{aligned} \beta \text {-}C_i = \{ x \in X_i : x \in \beta \text {-}S_i \wedge g(x)=f(x) \} \end{aligned}$$

(1)

$$\begin{aligned} \beta \text {-}I_i = \{ x \in X_i : \exists l \in \{1,\ldots ,m\}, x \in \beta \text {-}S_{l \ne i} \wedge g(x) \ne f(x) \} \end{aligned}$$

(2)

where $\beta \text {-}S_i$ is referred to as the $\beta -$strong region and contains instances with a high membership degree to the i-th decision class according to the neighborhood function. These instances are likely members of the target decision class since they are strong members of a neighborhood dominated by instances labeled with that class. Equation (3) mathematically formalizes this region,

$$\begin{aligned} \beta \text {-}S_i = \{ x \in X : \mu _i(x) \ge \beta \} \end{aligned}$$

(3)

such that $\alpha ,\beta \in [0,1]$ is a parameter to be specified by the user. Setting $\beta$ close to one will cause most instances to be excluded from the presumably correct/incorrect analysis, while setting $\beta$ close to zero will cause most instances to be considered as strong members of their neighborhood.

The $\beta$-presumably correct region $\beta \text {-}C_i$ contains instances that must satisfy two primary properties. Firstly, these instances have membership degrees in the i-th strong region that meet the constraints imposed by the $\beta$ parameter. Secondly, the decision classes determined by the function f(x) for these instances align with those computed by the function g(x) ($x \in X_i$ implies $g(x)=y_i$). Instances belonging to the strong region $\beta \text {-}S_{l \ne i}$ but having $f(x) \ne g(x)$ are considered presumably incorrect (assuming $f(x)=y_l$). Finally, instances that do not possess membership values fulfilling the membership constraint are neither labeled as presumably correct nor incorrect.

3 Presumably Correct Undersampling

In this section, we present the contributions of our paper, named the Presumably Correct Undersampling (PCU) method. This procedure starts with the assumption that there is a highly imbalanced classification problem with a clearly distinguished majority class. The intuition behind the PCU formalism is that we can safely replace instances that are considered presumably correct members of the majority decision class by prototypes. These instances do not define the decision boundaries of the classification problem, and their removal should not affect the discriminatory power of the data. Note that this assumption opposes the strategy used by the TLU method (Tomek, 1976), which removes pairs of instances from different classes that are each other’s closest neighbors. By removing such instances, the TLU method improves class separability and addresses challenges arising from overlapping or misclassified instances. However, while this brings evident benefits during the classifier’s training process, it may increase the difficulty of accurately classifying challenging instances when applying the classifier to unseen data. Similarly to the approach used by the TLU method, our algorithm could also remove the presumably incorrect instances belonging to the majority class. These instances are strong members of some other region, according to the neighborhood function, yet are labeled with the majority decision class. Therefore, they can be considered noisy instances rather than borderline instances, as they strongly belong to their respective neighborhoods. However, this paper focuses on the presumably correct instances only. Let us break the proposed algorithm into two main steps related to isolating the presumably correct instances and replacing them with prototypes.

Step 1. Determining the presumably correct and incorrect instances, as defined in Eqs. (1) and (2), requires defining a neighborhood function. In the original paper, Nápoles et al. [15] defined this function as the k-nearest neighbor classifier. Hence, an instance $x \in X$ will be included in $\beta \text {-}C_i$ if $g(x)=i$, $x \in \beta \text {-}S_i$ and $|\mathcal {N}_k(x) \cap X_i| / |X_i|$ is maximal for the i-th decision class, with $\mathcal {N}_k(x)$ being the k closest neighbors of x. The last condition might bring some issues for our algorithm since it is not required for the $\mathcal {N}_k(x)$ to be entirely included in $X_i$. In other words, x has some neighbors that do not belong to the i-th decision class. Let us redefine the concepts of presumably correct and incorrect sets based on a neighborhood function ensuring the full inclusion degree of $\mathcal {N}_k(x)$ in $X_i$. Hence, Eqs. (1) and (2) can be rewritten as follows:

$$\begin{aligned} \beta \text {-}C_i = \{ x \in X_i : x \in \beta \text {-}S_i \wedge \mathcal {N}_k(x) \subseteq X_i \}, \end{aligned}$$

(4)

$$\begin{aligned} \beta \text {-}I_i = \{ x \in X_i : \exists l \in \{1,\ldots ,m\}, x \in \beta \text {-}S_{l \ne i} \wedge \mathcal {N}_k(x) \subseteq X_l \}. \end{aligned}$$

(5)

Moreover, the membership function needed to define $\beta \text {-}S_i$ can be formalized in terms of the k-nearest neighbors as follows:

$$\begin{aligned} \mu _i(x) = \frac{{ \sum _{z \in \mathcal {N}_k(x)} \frac{1}{{d(x,z)}} \cdot \phi (g(x) = g(z)) }}{{ \sum _{z \in \mathcal {N}_k(x)} \phi (g(x) = g(z)) }} \end{aligned}$$

(6)

such that

$$\begin{aligned} \phi (g(x) = g(z)) = {\left\{ \begin{array}{ll} 1, &{} \text {if } g(x) = g(z) \\ 0, &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

(7)

Notice that simultaneously fulfilling that $\mathcal {N}_k(x) \subseteq X_i$ and $x \in \beta \text {-}S_i$ is key in the proposed method. The former ensures that all neighbors of the instance being analyzed belong to the majority class, while the latter ensures that the instance itself is a strong member of its neighborhood. Both constraints lead to pure and cohesive presumably correct decision sets.

Step 2. Once we have isolated the presumably correct instances associated with the class to be undersampled, we can gather them into p clusters using any clustering method. This procedure requires specifying the number of clusters in advance, although it can be automatically estimated using a clustering validation measure such as the Davies-Bouldin Index or the Silhouette Coefficient. As a rule of thumb, the number of clusters can be estimated as $p=\lfloor (1-r) \cdot |\beta \text {-}C_i| \rfloor$, where $r \in [0,1]$ is the imbalance ratio computed as the number of minority instances divided by the number of majority instances. Finally, the presumably correct instances are removed from the dataset and replaced p prototypes obtained from the discovered clusters, meaning that there will be a prototype per cluster. The prototypes will be either the cluster centers themselves or the instances reporting the closest distances to their cluster centers.

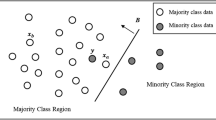
Figure 1 depicts the intuition of our algorithm for a three-class classification problem where the first decision class is represented by 100 instances, and the other two classes are represented by 50 instances each. Therefore, the purpose is to undersample the majority class as much as possible without damaging the decision space characterizing the problem. The algorithm first finds the presumably correct instances and then clusters them into p groups according to their similarity. Note that we only analyze instances belonging to the presumably correct region associated with the majority class.

Fig. 1.

Visual depiction of the proposed PCU algorithm for a toy example. Presumably correct instances belonging to the majority class are enclosed in colored circles. Note that these similarity classes or neighborhoods only contain instances that belong to the decision class to be undersampled.

Overall, the proposed PCU algorithm requires three parameters. The first parameter is the number of neighbors k used to build the neighborhood function $\mathcal {N}_k(x)$. The larger the number of neighbors, the fewer the number of presumably correct instances since finding pure neighborhoods will become more difficult. The second parameter, denoted as $\beta \in [0,1]$, specifies the minimum membership degree of an instance to be considered a strong member of its neighborhood. The last parameter concerns the reduction ratio $r \in [0,1]$, which indicates how many prototypes will be built from the isolated presumably correct instances. In short, larger values of this parameter translate into fewer prototypes. If $r=1.0$ then all presumably correct instances will be deleted without building any prototypes. If $r=0.0$ then each presumably correct instance will be deemed a prototype, thus inducing no modification to the dataset.

4 Experimental Simulations

In this section, we will conduct numerical simulations to validate the correctness of the proposed PCU method and contrast its performance against state-of-the-art algorithms devoted to undersampling the majority class.

First, let us illustrate the inner workings of our method in a two-dimensional dataset with three decision classes. In this problem, the majority class consists of 500 samples, the second largest decision class comprises 100 samples, and the third class contains 50 instances. Following the application of our undersampling method, the majority decision class is reduced to 130 instances, while the sizes of the other classes remain unchanged. Figures 2 and 3 show the instance distribution and the decision spaces for several classifiers, respectively.

Fig. 2.

Imbalanced three-class classification problem described by two numerical features. In the original problem, the first decision class is represented by 500 instances, the second by 100, and the third by 50. After applying our algorithm, the majority decision class narrows down to 130 instances.

Fig. 3.

Decision space of different classifiers for a three-class imbalanced problem before and after applying our algorithm. The number on the top of each sub-figure denotes Cohen’s kappa score on the test set.

Figure 3 shows the decision of several classifiers before and after undersampling. This toy dataset is split into training (80%) and test (20%) such that the former part is used to plot the decision spaces while the latter is used to test the classifiers’ generalization capabilities. It goes without saying that only the training data is undersampled and that the test data is kept untouched. The classifiers used in this simulation are Gaussian Naive Bayes, Random Forests with 100 estimators, Support Vector Machine classifier with a radial kernel and regularization parameter $c=1.0$, and Logistic Regression with $\ell _2$ regularization. As for the hyperparameter values of our algorithm, we arbitrarily set the number of neighbors as $k=10$, the confidence threshold as $\beta =0.8$, and the reduction ratio as $r=0.8$. In this experiment, we evaluate performance using Cohen’s kappa score [5], which is deemed a robust metric for imbalanced classification tasks. The results show that the modifications on the decision spaces of Support Vector Machine and Logistic Regression led to increased performance on the test set. Equally important is the fact that none of these classifiers reported any loss in performance after applying our undersampling method. Note that simplifying the dataset while keeping its properties is also valuable when it comes to improving the efficiency of machine learning methods.

Next, we will expand this experiment to a benchmarking set of imbalanced data. The initial step in our experimental methodology consists of generating 50 synthetic datasets with varying complexity levels. To generate these datasets, we resort to the make_classification function provided in the scikit-learn library [17]. This function creates datasets with clusters of normally distributed data points positioned around the vertices of a hypercube.

The general characteristics of the synthetic dataset are selected randomly from predefined intervals of possible values. The number of decision classes m is uniformly selected from the range [2, 5], while the number of samples s is selected from [5000, 10000]. The total number of features n is obtained from the multiplication of the number of decision classes m with a random factor uniformly selected from [5, 10]. From the total number of features, the number of informative features (n_1) is calculated as the floor of $p_i \times \texttt {n}$, where $p_i$ is uniformly sampled from [0.4, 0.8]. Similarly, the number of redundant features (n_2) is determined as the floor of $p_r \times (\texttt {n}-\texttt {n\_1})$, with $p_r$ uniformly sampled from [0.2, 0.4]. The number of repeated features (n_3) is set to zero since these are covered by the redundant ones in our experiment.

Moreover, the number of clusters per class c is uniformly selected from the interval [1, 5]. To introduce class imbalance in the dataset, the proportion of samples assigned to the majority class is set to 80%, while the remaining decision classes are equally represented. This function also provides the flexibility to add noise to the decision class through the flip_y parameter, which is assigned a value from the interval [0.0, 0.1]. The hypercube parameter takes random boolean values indicating whether the clusters are at the vertices of the hypercube or a random polytope. The dimension of the hypercube is determined by the number of informative features n_1. The length of the hypercube’s sides is twice the value of the parameter class_sep, which is randomly selected from [1, 2] and controls the spread of the decision classes.

The second step in our experimental methodology is to contrast the performance of a baseline classifier before and after the undersampling process. The selected baseline classifier is a Random Forest using the default hyperparameter values as reported in the scikit-learn library [17]. This setting allows us to compare the proposed PCU method against well-established undersampling techniques, such as Random Undersampling (RU), Cluster Centroids Undersampling (CCU), Edited Nearest Neighbors (ENN), Tomek Links Undersampling (TLU), and One-Sided Selection (OSS). For RU and CCU the method removes the 80% of the majority class, while for ENN, TLU, and OSS, we specify that the undersampling is only performed on the majority class. In the case of our algorithm, we use the same hyperparameter values as described above.

Figure 4 shows Cohen’s kappa scores (after performing 5-fold cross-validation) for all datasets before and after applying the undersampling methods. Besides coloring the scores to represent performance decrease (in red) or otherwise (in blue), we show the average score across all datasets reported for each method on the top of each violin plot. Our method reports the best performance overall, with the second smallest standard deviation after ENN. However, ENN is on par with TLU and OSS in terms of performance, while RU and CCU are more prone to lose performance after undersampling. It is worth mentioning that the average Cohen’s kappa score associated with the original datasets is 0.68, thus confirming the added value of using the PCU method.

Fig. 4.

Cohen’s kappa scores (denoted as colored dots) computed by each algorithm for the synthetic datasets used for simulation. Red dots mean that the performance decreased compared to the baseline, while blue dots mean that the performance improved or remained unchanged. (Color figure online)

In order to test whether there are statistically significant differences in performance among the undersampling algorithms, we apply the non-parametric Friedman test. The null hypothesis $H_0$ for this test is that the algorithms result in negligible performance differences. The resulting p-value = 0.0 after rounding, meaning that there are statistically significant differences in the group of algorithms being compared. Subsequently, we use a Wilcoxon signed-rank test to determine whether the significant differences come from our undersampling method compared to each of the other methods. The null hypothesis $H_0$ asserts that there are no notable variances in the algorithm’s performance among datasets, whereas the alternative hypothesis $H_1$ suggests the presence of significant differences. In addition, we use the Bonferroni-Holm post-hoc procedure to adjust the p-values produced by the Wilcoxon signed-rank test. This correction aims to control the family-wise error rate when performing a pairwise analysis by adjusting the p-values obtained in each comparison.

Table 1 portrays the results concerning the Wilcoxon test coupled with Bonferroni-Holm correction using the proposed PCU algorithm as the control method. In the table, $R^-$ indicates the number of datasets for which PCU reports less performance than the compared algorithm, while $R^+$ gives the number of datasets for which the opposite behavior is observed. The corrected p-values computed by Bonferroni-Holm advocate for rejecting the null hypotheses in all cases for a significance level of 0.05 (corresponding to a 95% confidence interval). The fact that the proposed PCU method reports the largest $R^+$ values and that the null hypotheses are rejected in all pairwise comparisons allows us to conclude the superiority of our proposal for the generated datasets.

Table 1. Results concerning the Wilcoxon pairwise test with Bonferroni-Holm correction using PCU as the control algorithm.

As the last experiment, we show the reduction ratio for all datasets in Fig. 5 after applying undersampling. The area denotes the reduction percentage across all datasets (the larger the area, the smaller the undersampled dataset). Firstly, it is clear that the PCU method reduces a larger number of instances than the ENN algorithm without affecting the classifier’s performance, as we concluded before. Secondly, although RU and CCU lead to the largest areas, they computed the worst prediction rates. Finally, TL and OSS barely modified the datasets, which explains their steady prediction rates.

Fig. 5.

Reduction ratio of instances that belong to the majority class reported by selected undersampling algorithms for each dataset. The numbers on the outer axis denote the indexes of synthetic datasets.

5 Concluding Remarks

This paper addressed the class imbalance problem in pattern classification using a data pre-processing algorithm that focuses on undersampling the majority class. The foundation of the proposed algorithm relies on the Presumably Correct Decision Sets, which differentiate between presumably correct instances (those with neighbors sharing the same class label), and presumably incorrect instances (those with neighbors belonging to a different decision class). By replacing the presumably correct instances from the majority class with prototypes, the algorithm aims to better balance the classes without significantly altering the decision boundaries. Reducing the majority class and retaining the decision boundaries would allow a classifier to increase its generalization capabilities. This approach contrasts with methods that remove pairs of instances from different classes that are closest neighbors. Overall, the algorithm provides a tool for mitigating class imbalance and offers potential improvements for the generalization capabilities of pattern classification models.

The simulations using 50 imbalanced problems confirmed that the PCU algorithm can effectively reduce the number of instances associated with the majority class. More importantly, we observed that the performance on unseen data remained unchanged or improved after undersampling. The observed reduction in the number of instances belonging to the majority class ranged from 8% to 60%, with certain cases exhibiting performance improvements of up to 28%. It is worth noting that achieving a substantial reduction in the dataset without sacrificing performance still holds great value, as it directly translates into improved efficiency when training classifiers or implementing post-hoc explanation methods. Furthermore, the findings indicate that the proposed algorithm outperforms existing state-of-the-art undersampling methods since these methods tend to either remove too many instances, leading to performance degradation or have minimal impact on the training data.

The primary limitation of our study concerns the lack of hyperparameter tuning since it will help improve the performance of all undersampling methods (ours included). In addition, conducting a sensitivity analysis to determine the impact of changing the number of neighbors, the confidence threshold, and the reduction ratio on the algorithm’s performance is paramount. We conjecture that tuning the reduction ratio and the confidence threshold can effectively be done with binary search instead of grid search. For instance, if the performance decreases for a given reduction ratio, it will continue to do so for values greater than such a cutting point. Finally, it will be interesting to study how different classifiers benefit from the proposed PCU method.