Abstract
Two fundamental properties of quantum states that quantum information theory explores are pseudorandomness and provability of destruction. We introduce the notion of quantum pseudorandom states with proofs of destruction (PRSPD) that combines both these properties. Like standard pseudorandom states (PRS), these are efficiently generated quantum states that are indistinguishable from random, but they can also be measured to create a classical string. This string is verifiable (given the secret key) and certifies that the state has been destructed. We show that, similarly to PRS, PRSPD can be constructed from any post-quantum one-way function. As far as the authors are aware, this is the first construction of a family of states that satisfies both pseudorandomness and provability of destruction.
We show that many cryptographic applications that were shown based on PRS variants using quantum communication can be based on (variants of) PRSPD using only classical communication. This includes symmetric encryption, message authentication, one-time signatures, commitments, and classically verifiable private quantum coins.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A Pesudorandom States family (PRS), introduced in [16]) is an efficiently samplable family of pure states such that for any polynomial t, t-copies of a (pure) quantum state \(\vert \phi \rangle \) sampled uniformly at random from the family is computationally indistinguishable from t-copies of a truly random state sampled from the Haar measure. On the other hand, a provably destructible family of quantum states is accompanied by two efficient quantum algorithms,  , and
, and  , such that running
, such that running  on a state \(\vert \phi \rangle \) sampled from the family, produces a classical proof
on a state \(\vert \phi \rangle \) sampled from the family, produces a classical proof  that can be verified using
that can be verified using  , such that given a copy of a sampled state \(\vert \phi \rangle \) one cannot output both, the state \(\vert \phi \rangle \) and a valid proof of destruction \(s_{\phi }\). Proofs of destructions as defined above (or variants of it) have served as a crucial property for many unclonable primitives, such as tokenized digital signatures [7, 12, 23], classically verifiable quantum money [18, 24], quantum lightning and its applications [13, 21, 27], one-shot signatures [1], etc.
, such that given a copy of a sampled state \(\vert \phi \rangle \) one cannot output both, the state \(\vert \phi \rangle \) and a valid proof of destruction \(s_{\phi }\). Proofs of destructions as defined above (or variants of it) have served as a crucial property for many unclonable primitives, such as tokenized digital signatures [7, 12, 23], classically verifiable quantum money [18, 24], quantum lightning and its applications [13, 21, 27], one-shot signatures [1], etc.
As far as the authors are aware, there is no construction of a family of states that satisfies both pseudorandomness and provability of destruction. Previous constructions of provably destructible distributions were provably not pseudorandom. This stems from the fact that such techniques involved sampling a state that maintains its security only when a single copy is given. In fact, in most of these constructions (such as in [7, 12]), given O(n) copies of the sampled state, it is possible to not only tell the state from a Haar-random state but to completely characterize and efficiently generate the sampled state. On the side of pseudorandomness, previous techniques focused on sampled states that are uniform (or close to uniform) superpositions, with randomly sampled phases of the amplitudes. Since all known proof generation mechanisms  in the literature are essentially, measurements in the computational basis, these constructions with uniform superposition can not be provably destructible. In this work, we study how to combine both these notions in a single primitive.
in the literature are essentially, measurements in the computational basis, these constructions with uniform superposition can not be provably destructible. In this work, we study how to combine both these notions in a single primitive.

In classical cryptography, one-way functions (OWF) are considered a minimal assumption for computational-cryptography, and they are also sufficient for many applications. In the quantum setting, in contrast, (post-quantum) one-way functions are sufficient but do not appear to be necessary for a variety of cryptographic tasks such as symmetric encryption, digital signatures, message authentication codes, and commitments. Specifically, Ref. [16] showed that one-way functions are sufficient to build \(\textsf {PRS}\), but Kretschmer [17] showed a black-box separation in the other direction, thus implying that OWFs are not necessary for \(\textsf {PRS}\). Several recent works showed that \(\textsf {PRS}\) suffices to imply the aforementioned cryptographic applications (or variants thereof), without using OWF. For example, statistically-binding bit-commitment protocols have been shown based on \(\textsf {PRS}\) [4, 19] (see Sect. 1.4 for other related works). However, these constructions used a different syntax than their classical counterparts—in particular in requiring quantum communication.
One of the aims of this work is to investigate whether this change is necessary:

Indeed, this question has also been recently addressed by Ananth, Gulati, Qian and Yuen [2], who have shown statistically binding bit commitment and pseudo-encryption with classical communication. Their constructions were based on variants of \(\textsf {PRS}\) (namely, short output \(\textsf {PRS}\) and short output \(\textsf {PRFS}\)).
1.1 Our Results
Our first contribution, in Sect. 3, is defining the notion of proofs of destruction in the context of pseudorandom states, which addresses the first question raised above, see Page 2. In a \(\textsf {PRS}\) with proof of destruction (PRSPD), we augment a  algorithm, which takes the pseudorandom state, and generates a classical proof; and a
algorithm, which takes the pseudorandom state, and generates a classical proof; and a  algorithm, which takes a proposed proof and a key, and either accepts or rejects. We require that valid proofs should be accepted with certainty. In terms of security, we add the \(\mathsf {Unforgeability\text {-}of\text {-}proofs}\) requirement, which guarantees that given t copies of the pseudorandom state, it should be hard to produce \(t+1\) distinct proofs of destruction. We extend the notion of proofs of destruction to a variant of \(\textsf {PRS}\), called pseudorandom function-like states (PRFS), that was introduced in [4] (see Sect. 1.4 for further discussion). In a \(\textsf {PRFS}\), the seed k should allow to efficiently generate a state for any input x, such that the states generated for different x’s should jointly be indistinguishable from a random state. Namely, an adversary can choose \(x_1,\ldots ,x_m\), and should not be able to distinguish between \(\bigotimes _{i\in [m]} \vert \psi _{k,x_i} \rangle \), where \(\vert \psi _{k,x_i} \rangle \) are generated from the \(\textsf {PRFS}\) family, and \(\bigotimes _{i\in [m]} \vert \varphi _{x_i} \rangle \) where \(\vert \varphi _{x_i} \rangle \) is sampled from the Haar measure. We import the notion of \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) to \(\textsf {PRFS}\) and define the notion of \(\textsf {PRFSPD}\). We then proceed, in Sect. 4, to show how to construct \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\) from any post-quantum one-way function, which requires extending existing proof techniques for the construction of these primitives. Currently, we do not have a candidate construction of \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\) that does not use one-way functions directly.
algorithm, which takes a proposed proof and a key, and either accepts or rejects. We require that valid proofs should be accepted with certainty. In terms of security, we add the \(\mathsf {Unforgeability\text {-}of\text {-}proofs}\) requirement, which guarantees that given t copies of the pseudorandom state, it should be hard to produce \(t+1\) distinct proofs of destruction. We extend the notion of proofs of destruction to a variant of \(\textsf {PRS}\), called pseudorandom function-like states (PRFS), that was introduced in [4] (see Sect. 1.4 for further discussion). In a \(\textsf {PRFS}\), the seed k should allow to efficiently generate a state for any input x, such that the states generated for different x’s should jointly be indistinguishable from a random state. Namely, an adversary can choose \(x_1,\ldots ,x_m\), and should not be able to distinguish between \(\bigotimes _{i\in [m]} \vert \psi _{k,x_i} \rangle \), where \(\vert \psi _{k,x_i} \rangle \) are generated from the \(\textsf {PRFS}\) family, and \(\bigotimes _{i\in [m]} \vert \varphi _{x_i} \rangle \) where \(\vert \varphi _{x_i} \rangle \) is sampled from the Haar measure. We import the notion of \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) to \(\textsf {PRFS}\) and define the notion of \(\textsf {PRFSPD}\). We then proceed, in Sect. 4, to show how to construct \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\) from any post-quantum one-way function, which requires extending existing proof techniques for the construction of these primitives. Currently, we do not have a candidate construction of \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\) that does not use one-way functions directly.
Finally, in Sect. 5, we show how pseudorandom states (and function-like states) with proof of destruction can be used to achieve almost all of the existing known applications of pseudorandom states (and function-like states, respectively), without the need for quantum communication, thereby addressing the second question mentioned above, see Page 2. Specifically, we construct:
-
1.
Length-restricted one-time secure digital signatures, and classically-verifiable private quantum coinsFootnote 1 from any \(\textsf {PRSPD}\).
-
2.
A \(\textsf{computational}\text {-}\textsf{hiding}\) and \(\textsf{statistically}\text {-}\textsf{binding}\) bit commitment from \(\textsf {PRSPD}\) in which the proofs satisfy some nice properties, which we denote by \(\textsf {PRSNPD}\)—see the full version for details. While we do not know how to construct such \(\textsf {PRSNPD}\) from \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\), our construction satisfies this niceness property.
-
3.
\(\textsf{CPA}\) symmetric encryption (Sect. 5.2) and strong-\(\textsf{CMA}\) \(\textsf{MAC} \) (Sect. 5.1) from any \(\textsf {PRFSPD}\). Note that this form of encryption is known to imply garbled circuits (see the full version for more details).
1.2 Our Techniques
Our construction of \(\textsf {PRSPD}\) is based on the following observation. Prior constructions starting with [16] showed that a uniform superposition over all computational basis elements, with a random phase, constitutes a \(\textsf {PRS}\). Formally, the family \(\vert \psi _k \rangle =\frac{1}{\sqrt{N}}\sum _{y\in \{0,1\}^n } \omega _N^{\textsf {PRF}_k(y)}\vert y \rangle \) is a \(\textsf {PRS}\) family whenever \(\textsf {PRF}_k\) is a post-quantum PRF from n bits to n bits, where \(N=2^n\) and \(\omega _N\) is the N-th root of unity. We show that a state which is supported on a pseudorandom subset of computational basis elements is still a \(\textsf {PRS}\). More precisely, for a pseudorandom permutation \(\textsf {PRP}\) on 4n bits, let \(A_{k'}=\{\textsf {PRP}_{k'}(z||0^{3n}) :z\in \{0,1\}^n\}\). We prove that the following states form a pseudorandom family:
This modification allows us to generate a proof of destruction as follows. The state \(\vert \psi _{k,k'} \rangle \) is measured in the computational basis, resulting in a (uniformly random) element of \(A_{k'}\), which we denote by p. The verification procedure for p is to apply \(\textsf {PRP}_{k'}^{-1}(p)\) and checking that the result is of the form \(z|| 0^{3n}\) for some string z. We show that this construction satisfies the \(\mathsf {Unforgeability\text {-}of\text {-}proofs}\) property.
We observe a property of our construction from which it is easy to deduce both—the pseudorandomness property and the unforgeability of proofs property. We recall a property of the Haar-random distribution over quantum states. The following distributions (over quantum states) are equivalent: (i) Sample an n-qubit Haar-random state and output t copies of this state. (ii) Sample t elements from \(\{ 0, 1 \}^n\), according to some distribution, and output a superposition over all t! permutations of this t-tuple. In fact, the distribution can be i.i.d uniform over the domain, with only a negligible effect on the outcome.
Now, if we sample the t elements not from the entire domain, but rather from a large enough random sub-domain, the distribution over tuples will remain statistically indistinguishable. We can apply this logic twice: First, to derive pseudorandomness, since a random state over a random subdomain is indistinguishable from a random state over the entire domain. Second, to derive the unforgeability of proofs, since providing t samples of the \(\textsf {PRSPD}\) state is statistically indistinguishable from a process that only uses t classical values from the sub-domain. Thus, coming up with an additional element in this random sub-domain can be done with at most negligible probability for classical information-theoretic reasons. We further show that experiment (ii) above is statistically close to experiment (iii): Sampling an exponential size subdomain A and a random function f and preparing t copies of the state \(\vert \psi _{A,f} \rangle \propto \sum _{x \in A}\omega _N^{f(x)}\vert x \rangle \). Experiment (iii) and experiment (iv) in which t copies of the \(\textsf {PRSPD}\) states in Eq. (1) can now be seen to be computationally indistinguishable, by the pseudorandomness properties of the \(\textsf {PRF}\) and \(\textsf {PRP}\) functions. Transitions (ii)-(iv) are formalized in our main technical lemma, Lemma 6.
Extending this idea to \(\textsf {PRFSPD}\) is done in a straightforward manner, starting from the \(\textsf {PRFS}\) construction of [2]. Our \(\textsf {PRFSPD}\) family can be thought of as \(\vert \psi _{(k,k'),x} \rangle =\frac{1}{\sqrt{N}}\sum _{y\in A_{k',x}} \omega _N^{\textsf {PRF}_k(x,y)}\vert y \rangle \), where \(A_{k',x}=\{\textsf {PRP}_{k'}(y|| x || 0^{3n}) :y\in \{0,1\}^n \}\) for \(x \in \{0,1\}^n\). The destruction is done as before, and verification checks that p has the form \(y|| x || 0^{3n}\).
How to Use Pseudorandom States with Proof of Destruction. In many cases, a template can be used to remove the quantum communication from a protocol involving pseudorandom states. Several protocols use \(\textsf {PRS}\) in the following manner. In the first part of the protocol, a pseudorandom state \(\vert \psi _{k} \rangle \) is generated and sent via quantum communication. In a later step of the protocol, a testing procedure is applied to check if the state is indeed \(\vert \psi _k \rangle \). In order to remove the quantum communication, we send the (classical) proof of destruction of it (instead of the state itself). Furthermore, we replace the testing whether the state is the “correct” state, with verifying that the proof of destruction is valid. This approach can also be applied with \(\textsf {PRFS}\), where the state is \(\vert \psi _{k,x} \rangle \) used.
Next, we demonstrate the use of the template above with a concrete example. Ref. [4] constructs a MAC scheme using \(\textsf {PRFS}\), in which the secret key is a random k,  generate a quantum signature \(\vert \psi _{k,m} \rangle \), and
generate a quantum signature \(\vert \psi _{k,m} \rangle \), and  is done by testing procedure discussed above, which tests whether \(\vert \varphi \rangle \) is the expected state \(\vert \psi _{k,m} \rangle \). In our scheme (see Sect. 5.1),
is done by testing procedure discussed above, which tests whether \(\vert \varphi \rangle \) is the expected state \(\vert \psi _{k,m} \rangle \). In our scheme (see Sect. 5.1),  is done by preparing \(\vert \psi _{k,m} \rangle \), and the classical signature is the proof of destruction, denoted p, of this state. Clearly, the signature can now be sent via a classical channel. The testing procedure above is replaced with checking that p is a valid proof of destruction for (k, m).
is done by preparing \(\vert \psi _{k,m} \rangle \), and the classical signature is the proof of destruction, denoted p, of this state. Clearly, the signature can now be sent via a classical channel. The testing procedure above is replaced with checking that p is a valid proof of destruction for (k, m).
The template above is indeed useful as a conceptual framework, but applying it sometimes requires consideration of the specifics of the primitives. Some specific challenges that need to be addressed are as follows.
-
1.
Pseudorandom states are pseudorandom as quantum states, but the proofs of destruction are not required to be pseudorandom strings. For example, one can easily transform a \(\textsf {PRSPD}\) scheme to one in which the first bit of the proof of destruction is always 0.
This issue comes up in the context of bit-commitment. Reference [19] shows a construction that can be viewed as a quantum analog of Naor’s commitments from PRG. There, we need to make the additional assumptions that the proofs are pseudorandom in order to prove the hiding property—see the full version for details.
Recall that Naor’s construction also requires a length-tripling PRG to prove the statistical binding. For analogous reasons, in our setting, we need a \(\textsf {PRFSPD}\) in which every key k accepts only a small fraction of the potential proofs.
We define a \(\textsf {PRSPD}\) in which the proofs of destruction satisfy these nice properties as \(\textsf {PRSNPD}\).
-
2.
Pseudorandom states are known to be uncloneable [16, Theorem 2], but the proofs of destruction are classical and, therefore, can trivially be copied. We are only guaranteed that generating new proofs of destruction is hard. This difference means that for our quantum coins scheme to be secure, the bank needs to keep a copy of the proofs that were already accepted, so these would be rejected in further attempts. In other words, unlike the quantum coin scheme proposed by [16], our quantum coin protocol is stateful—see the full version for details.
-
3.
It can be shown that \(\textsf {PRS}\) are non-invertible in the following sense: Given \(\vert \psi _k \rangle \), one cannot find \(k'\) such that \(\vert \psi _{k'} \rangle \) has a non-negligible overlap with \(\vert \psi _k \rangle \) [19, Lemma 4.1]. An analogous property does not necessarily hold for proofs of destruction: Given a proof p for \(\vert \psi _k \rangle \), one might be able to find \(k'\) such that p is a valid proof of this destruction for \(k'\). For example, given a \(\textsf {PRSPD}\) scheme, one can modify it so \(k'=00\ldots 0\) accepts all proofs of destruction. Since that particular \(k'\) has a negligible probability of getting sampled as the key, it has no effect on the security of the scheme. But now, given a proof of destruction p, it is trivial to find a \(k'\) such that the proof of destruction is accepted. This issue arises in the context of one-time digital signatures, which we expand upon next.
To illustrate an example of such a challenge, let us describe our construction of one-time signatures from \(\textsf {PRSPD}\). We recall Lamport’s one-time signature scheme and assume that we only wish to sign one-bit messages (the extension to multiple bits is by repetition, as in the classical case). The idea in Lamport’s OWF-based scheme is to sample uniformly random \(x_0, x_1\) as the signing key, set \(y_0=f(x_0), y_1=f(x_1)\) as a verification key, and set the signature on message \(m\in \{0,1\}\) to be \(x_m\). This was adapted to \(\textsf {PRS}\) by [19], by replacing f with the \(\textsf {PRS}\) generator algorithm.
We wish to convert our quantum verification key to being classical using \(\textsf {PRSPD}\). We achieve this by replacing the \(\textsf {PRS}\) states with their respective proofs of destruction \(p_0, p_1\). The signature will be the key associated with the proof of destruction. However, contrary to the classical and \(\textsf {PRS}\) settings, we must take a different approach here. A forgery here consists of a \(\textsf {PRSPD}\) key \(k'_m\) which verifies \(p_m\); indeed, if we were guaranteed that \(k'_m=k_m\) then we would have been done since unforgeability of proofs would have been used in order to complete the security proof. However, this is not the case, and the unforgeability of proofs alone is insufficient: see Item 3 above.
To rule out “junk keys”—keys which accept too many proofs of destruction—we apply two modifications: the public key consists of a large number of proofs \(\boldsymbol{p}_m\) for every value of m (where all proofs of destruction are generated using the same key), instead of just one. We know that all of these proofs of destruction will get accepted by the \(\textsf {PRSPD}\) verification by the key that generated these states. We also modify the signature verification algorithm so that given a signature \(k'_m\), it first samples a large polynomial number of proofs of destruction with freshly random keys, and makes sure that \(k'_m\) is not verifying garbage (honestly generated keys will pass this test with overwhelming probability). Only after passing this test will the forgery be tested against \(\boldsymbol{p}_m\). One can easily see that this method rules out simple “junk keys” that accept all proofs, as in the example described above. The full security proof uses a hybrid argument where the public key is not generated using a key \(k_m\) of the \(\textsf {PRSPD}\), but instead, it is generated by applying the destruction algorithm to a Haar random quantum state.Footnote 2 This can only have a negligible change on the forgery probability by the pseudorandomness of the \(\textsf {PRSPD}\). Interestingly, the construction by [19] did not use the pseudorandomness property and relied on a weaker notion called one-way state generators. We then show that an adversary which receives such “garbage” proofs \(p_m\) (i.e. proofs which are generated by the proof of destruction procedure on Haar random states) cannot provide forgery.
1.3 Open Problems
-
A primary motivation to study pseudorandom states is that it seems as a weaker assumption than one-way functions, on which quantum cryptography could be based upon. Unfortunately, this separation result only holds for some of the \(\textsf {PRS}\)-variants. No such separation result is known for short-output \(\textsf {PRS}\) and short-output \(\textsf {PRFS}\). Note that some of the applications prior to ours rely upon those. Similarly, we did not prove a similar separation for \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\), and these challenges are left as an open problem.
-
Does \(\textsf {PRSPD}\) imply short-input \(\textsf {PRFSPD}\), i.e., \(\textsf {PRFSPD}\) with logarithmic input length? Ref. [4] constructs short-input \(\textsf {PRFS}\) from \(\textsf {PRS}\) generically by measuring the first \(\log (\lambda )\) qubits and post-selecting the outcome being the input. The same approach may not work in the case of \(\textsf {PRFSPD}\) and \(\textsf {PRSPD}\) because the post-selection procedure as proposed in [4] may not commute with the
 algorithm for general \(\textsf {PRSPD}\). An alternate yet related approach would be to run the
algorithm for general \(\textsf {PRSPD}\). An alternate yet related approach would be to run the  algorithm on the input state without measurement, then measure only the first \(\log (\lambda )\) qubits, post-select on the outcome being the input, and output the state on the unmeasured registers as the \(\textsf {PRFSPD}\) state.
algorithm on the input state without measurement, then measure only the first \(\log (\lambda )\) qubits, post-select on the outcome being the input, and output the state on the unmeasured registers as the \(\textsf {PRFSPD}\) state.The hope is that if the starting state was
 random, then the state on the unmeasured bits will be Haar random. However, the destruct algorithms may use ancillae qubits, and therefore the overall process becomes non-unitary, even before the measurement. Since non-unitary processes do not preserve
random, then the state on the unmeasured bits will be Haar random. However, the destruct algorithms may use ancillae qubits, and therefore the overall process becomes non-unitary, even before the measurement. Since non-unitary processes do not preserve  -random property, if we measure the first \(\log (\lambda )\) registers, the state on the rest of the registers might not be statistically close to
-random property, if we measure the first \(\log (\lambda )\) registers, the state on the rest of the registers might not be statistically close to  random.
random.
1.4 Related Works
Quantum forms of pseudorandomness have seen rapid development, which we summarize in this section. All the results mentioned (except the concurrent result of [3]), along with our main results are depicted in Fig. 1.
The study of pseudorandom state generators (\(\textsf {PRS}\)) was initiated by Ji, Liu, and Song [16]. They proved a construction based on the existence of post-quantum one-way functions. Ji, Liu, and Song’s \(\textsf {PRS}\) construction were simplified in Ref. [10].
Kretschmer [17] proved a separation between one-way functions and \(\textsf {PRS}\)s: there exists a quantum oracle relative to which \(\textsf {PRS}\)s exist, but one-way functions do not exist. In other words, there is no black-box reduction from \(\textsf {PRS}\) to one-way functions (while a black-box reduction in the other direction is implied by [16]).
Several variants of \(\textsf {PRS}\) have been introduced, all of which are implied by post-quantum one-way functions. These different variants will play an important role when we discuss the applications. In Ref. [11], the authors show how to construct a scalable \(\textsf {PRS}\) based on OWFs; in this context, scalability means that for any function \(n(\lambda )\le \lambda \), one can construct a \(\textsf {PRS}\) with \(n(\lambda )\) qubits. Perhaps counter-intuitively, and unlike pseudorandom generators, constructing pseudorandom states with a smaller number of qubits n seems harder (and definitely does not follow from the definition).
In [4], Ananth, Qian, and Yuen define pseudorandom function-like states (PRFS). An (d, n)-\(\textsf {PRFS}\) generator receives a key \(k\in \{0,1\}^\lambda \) and an input \( x\in \{0,1\}^d\) and outputs an n-qubit stateFootnote 3. In the security game, the adversary can choose (in advance) a set of inputs \(x_1,\ldots ,x_m\); the challenger either picks a random k and returns the \(\textsf {PRFS}\) states associated with \((k,x_1),(k,x_2),\ldots ,(k,x_m)\), or samples a Haar random state for each distinct \(x_i\), and send the states to the adversary. The adversary needs to distinguish between these two cases. They show how to construct a (n, d)-\(\textsf {PRFS}\) for \(d=O(\log \lambda )\) from any \((n+d \lambda )\)-\(\textsf {PRS}\). We refer to \(\textsf {PRFS}\) in that regime (namely, \(d=O(\log \lambda )\)) as short input \(\textsf {PRFS}\). They show how to construct a \(\textsf {PRFS}\) with \(\omega (\log (\lambda ))\) input length, which we refer to as long input \(\textsf {PRFS}\), from any OWF. They also show that long input \(\textsf {PRFS}\) is separated from OWFs. It is not known how to construct long input \(\textsf {PRFS}\) from a short input \(\textsf {PRFS}\). It is known that, similarly to vanilla \(\textsf {PRS}\), short and long input \(\textsf {PRFS}\) are separated from post-quantum one-way functions [4].
Several applications of \(\textsf {PRS}\)s have been shown. In [16], it was shown that \(\textsf {PRS}\) implies a private quantum coin scheme—i.e., a private quantum money scheme in which all the quantum money states are exact copies. In [6], an almost public quantum coin scheme was shown based on the existence of any private coin scheme. In this context, public means that users can verify a quantum coin without the bank. The scheme was almost public because it has several limitations. For example, it only achieves rational unforgeability; and the users must have coins in order to verify other coins. Note that there are no other public quantum money schemes based on one-way functions. Morimae and Yamakawa [19] construct a length-restricted one-time signature (also known as Lamport signature) with a quantum public key.
\(\textsf {PRFS}\) has several applications, which depend on the parameters of the \(\textsf {PRFS}\). We start with those which are implied by the weakest form, namely, short input \(\textsf {PRFS}\). Reference [4] construct a symmetric pseudo-encryption with quantum ciphers, which achieves one-time security. Pseudo-encryption means that the key is shorter than the length of the encrypted message—which is impossible to achieve unconditionally. This result requires a \(\omega (\log \lambda )\)-\(\textsf {PRS}\) or alternatively, an (n, d)-\(\textsf {PRFS}\) with \(d>\log \lambda \) and \(n=\omega (\log \lambda )\). As observed by [4], garbled circuits can be constructed from the symmetric pseudo-encryption mentioned above. Note that in this construction, the original circuit is classical, and the resulting garbled circuit is quantum. They also construct a statistically binding quantum bit-commitment from a \((2\log \lambda )+\omega (\log \log \lambda ))\)-\(\textsf {PRS}\) (or, alternatively, an (n, d)-\(\textsf {PRFS}\) satisfying \(2^d\cdot n\ge 7 \lambda \)); and by adapting the result in [5], they construct multi-party computation in the dishonest majority setting based on the same assumption.
Reference [4] also shows three other constructions based on long input \(\textsf {PRFS}\): Symmetric encryption scheme secure against selective CPA with quantum ciphers based on \((\omega (\lambda ),\omega (\lambda ))\)-\(\textsf {PRFS}\); a reusable MAC with quantum tags, which is length restricted to \(\ell (\lambda )\) bits, based on a (d, n)-\(\textsf {PRFS}\) with \(d(\lambda )\ge \ell (\lambda )\) and \(d=\omega (\log \lambda )\);
Recently, in [2], the authors report on statistically binding commitments and pseudo-encryption with classical communication. Their construction is based on short output \(\textsf {PRFS}\), namely, \(\log (\lambda )\) output and input sizes. In a concurrent and independent work [3], the authors showed a construction of non-adaptive CPA-secure symmetric encryption with classical ciphertexts from short output \(\textsf {PRFS}\) (this result is yet to be added in Fig. 1).
The notion of a \(\textsf {PRS}\) was used outside the context of cryptography in the study of the wormhole growth paradox [8] and quantum machine learning.
From the results mentioned so far, there is no indication that \(\textsf {PRS}\) (or any of its variants) are minimal assumptions for the cryptographic task that they can be used to achieve. Two recent works address this aspect: (a) Ref. [9] shows that EFI pairs—efficiently samplable, statistically far but computationally indistinguishable pairs of mixed quantum states—are equivalent to statistically binding quantum commitments, oblivious transfer, and several other functionalities. (b) Ref. [19, 20] proved that a one-way state generator (OWSG) is equivalent to one-time signatures with quantum public keys.
We mention that OWSGs are known to be implied from private quantum coins and that a variant called secretly-verifiable and statistically invertible one-way state generator (SV-SI-OWSG) is equivalent to EFI [20].
2 Notations, Standard Cryptographic Definitions and Facts
For any finite set S, we use \(s\xleftarrow {u} S\) to denote uniformly random sampling from the set S. Next, we recall the following result for quantum-secure Pseudorandom functions (PRF) and pseudorandom permutations (PRP), i.e., Pseudorandom functions and permutations that are secure against efficient quantum adversaries making quantum queries to the oracles, see the full version for the rigorous definitions.
Theorem 1
([25, 26]). \(\textsf {PRF}\)s and \(\textsf {PRP}\)s exist if quantum-secure one-way functions exist.
Quantum Information: For any \(n\in \mathbb {N}\), we use \(\mathcal {H}_n\) to denote the Hilbert space on n-qubit registers, i.e., \(\mathcal {H}_n={\mathbb {C}^2}^{\otimes n}\), and N to denote N, the dimension of \({\mathbb {C}^2}^{\otimes n}\). Note that the optimal distinguishing probability between two n-qubit quantum (possibly mixed) states \(\rho _0\) and \(\rho _1\) is given by their trace distance \({\text {D}}(\rho _0, \rho _1)\), defined as
We now turn to discuss standard properties of symmetric subspaces; for an in-depth discussion, see [15]. For Hilbert space \(\mathcal {H}_n\) of dimension N, i.e., it represents an n-qubit system, and integer t, we use \(\vee ^t \mathcal {H}_n\) to denote the symmetric subspace of \(\mathcal {H}_n^{\otimes t}\), the subspace of states that are invariant under permutations of the subsystems. Let \(\mathcal {X}\) be the set \(\{0,1,\ldots ,N-1\}\) such that \({\mathcal {H}_n}\) is the span of \(\{ \vert x \rangle \}_{x\in \mathcal {X}}\).
For any subset \(A\subset \mathcal {X}\), we use \(\mathcal {H}_A\) to denote the subspace \(\textsf{Span} (A)\), and \(\vee ^t \mathcal {H}_A\) to denote the symmetric subspace of \(\mathcal {H}_A^{\otimes t}\).
For any \(t\in \mathbb {N}\), let \(\mathbb {N}^{A }_{t}\) be the set of all vectors \(\boldsymbol{z}\) in \(\mathbb {N}^A\) such that \(\sum _{j\in A}z_j=t\). We will abbreviate \(\mathbb {N}^{A}_{t}\) as \(\mathbb {N}_t\) for the special case \(A=\mathcal {X}\). For any \(\textbf{x}=(x_1,x_2,\ldots ,x_t)\in A^t\), denote \(k(\textbf{x})\) to be the associated vector in \(\mathbb {N}^{A}_{t}\), i.e., the \(y^{th}\) coordinate of \(\boldsymbol{z}\) is the number of \(\textbf{x}_j\) that are y. For any \(\boldsymbol{z}\in \mathbb {N}_t \), define the state
For \(\boldsymbol{z}\in \mathbb {N}^{A}_{t}\), \(\vert \text {Sym}_t^{\boldsymbol{z}} \rangle \) can be written as \(\sqrt{\frac{1}{\left( {\begin{array}{c}t\\ \boldsymbol{z}\end{array}}\right) }} \sum _{x\in A^t:k(x)=\boldsymbol{z}} \vert x \rangle .\)
The set of states
forms an orthonormal basis of the symmetric subspace \(\vee ^t \mathcal {H}_A\) and \(\vee ^t {\mathcal {H}_n}\), respectively. This implies that the dimension of the symmetric subspace \(\vee ^t \mathcal {H}_A\) is \(|\mathbb {N}^{A}_{t}|=\left( {\begin{array}{c}|A|+t-1\\ t\end{array}}\right) \). In particular,
Let \(\varPi ^\text {Sym}_t\) be the projection onto the symmetric subspace \(\vee ^t {\mathcal {H}_n}\), and for any \(A\subset \mathcal {X}\), let \(\varPi ^{\text {Sym},A}_t\) be the orthogonal projection onto \(\vee ^t \mathcal {H}_A\).
Let \(\mu _{\mathcal {H}_n}\) be the Haar measure on \({\mathcal {H}_n}\), and \(\mu _{\mathcal {H}_A}\) be the induced measure on \(\mathcal {H}_A\), we have
3 Pseudorandom States and Function-Like States with Proofs of Destruction
In this section, we define pseudorandom states and function-like states with proofs of destruction and study some important properties and distributions related to them.
3.1 Core Definitions
Definition 1
(Pseudorandom state generator with proofs of destruction). A \(\textsf {PRSPD}\) scheme with key-length \(w(\lambda )\), output length \(n(\lambda )\) and proof length \(c(\lambda )\) is a tuple of \(\textsf {QPT}\) algorithms  with the following syntax:
with the following syntax:
-
1.
 : takes a key \(k\in \{0,1\}^{w(\lambda )}\), and outputs an \(n(\lambda )\)-qubit pure stateFootnote 4 \(\vert \psi _k \rangle \).
: takes a key \(k\in \{0,1\}^{w(\lambda )}\), and outputs an \(n(\lambda )\)-qubit pure stateFootnote 4 \(\vert \psi _k \rangle \). -
2.
 : takes an \(n(\lambda )\)-qubit quantum state \(\vert \phi \rangle \), and outputs a \(c(\lambda )\)-bit classical string, p.
: takes an \(n(\lambda )\)-qubit quantum state \(\vert \phi \rangle \), and outputs a \(c(\lambda )\)-bit classical string, p. -
3.
 : takes a key \(k\in \{0,1\}^{w(\lambda )}\), a \(c(\lambda )\)-bit classical string p and outputs a boolean output b.
: takes a key \(k\in \{0,1\}^{w(\lambda )}\), a \(c(\lambda )\)-bit classical string p and outputs a boolean output b.
Correctness. A \(\textsf {PRSPD}\) scheme is said to be correct if

Security.
-
1.
\(\textsf {Pseudorandomness:}\) A \(\textsf {PRSPD}\) scheme is said to be pseudorandom if for any \(\textsf {QPT}\) adversary \(\mathcal {A}\), and any polynomial \(m(\lambda )\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\), such that

-
2.
\(\mathsf {Unforgeability\text {-}of\text {-}proofs} \): A \(\textsf {PRSPD}\) scheme satisfies \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) if for any \(\textsf {QPT}\) adversary \(\mathcal {A}\) in forging game (Game 1), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that
$$\begin{aligned} \Pr [\textsf{Forging}\text {-}\textsf{Exp}^{\mathcal {A},\textsf {PRSPD}}_{\lambda } =1]=\textsf{negl}{\left( {\lambda }\right) }. \end{aligned}$$

Definition 2
(Pseudorandom function-like state generator with proofs of destruction). A \(\textsf {PRFSPD}\) scheme with key-length \(w(\lambda )\), input-length \(d(\lambda )\), output length \(n(\lambda )\) and proof length \(c(\lambda )\) is a tuple of \(\textsf {QPT}\) algorithms  with the following syntax:
with the following syntax:
-
1.
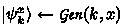 : takes a key \(k\in \{0,1\}^w\), an input string \(x\in \{0,1\}^{d(\lambda )}\), and outputs an n-qubit pure state \(\vert \psi ^x_k \rangle \).
: takes a key \(k\in \{0,1\}^w\), an input string \(x\in \{0,1\}^{d(\lambda )}\), and outputs an n-qubit pure state \(\vert \psi ^x_k \rangle \). -
2.
 : takes an n-qubit quantum state \(\vert \phi \rangle \) as input, and outputs a c-bit classical string, p.
: takes an n-qubit quantum state \(\vert \phi \rangle \) as input, and outputs a c-bit classical string, p. -
3.
 : takes a key \(k\in \{ 0,1 \}^w\), a d-bit input string x, a c-bit classical string p and outputs a Boolean output b.
: takes a key \(k\in \{ 0,1 \}^w\), a d-bit input string x, a c-bit classical string p and outputs a Boolean output b.
Correctness. A \(\textsf {PRFSPD}\) scheme is said to be correct if for every \(x\in \{0,1\}^{d}\),

Security.
-
1.
\(\textsf {Pseudorandomness:}\) A \(\textsf {PRFSPD}\) scheme is said to be quantum adaptively pseudorandom if for any \(\textsf {QPT}\) adversary \(\mathcal {A}\) there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\), such that the following absolute value is bounded by \(\textsf{negl}{\left( {\lambda }\right) }\),
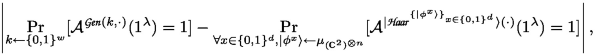 (8)
(8)where \(\forall x\in \{0,1\}^d\),
 outputs \(\vert \phi ^x \rangle \). Here
outputs \(\vert \phi ^x \rangle \). Here  represents that \(\mathcal {A}\) gets classical oracle access to
represents that \(\mathcal {A}\) gets classical oracle access to  .
. -
2.
\(\mathsf {Unforgeability\text {-}of\text {-}proofs} \): A \(\textsf {PRFSPD}\) scheme satisfies \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) if for any \(\textsf {QPT}\) adversary \(\mathcal {A}\) in forging game (Game 2), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that
$$ \Pr [\textsf{Forging}\text {-}\textsf{Exp}^{\mathcal {A},\textsf {PRFSPD}}_{\lambda } =1] = \textsf{negl}{\left( {\lambda }\right) }. $$
Remark 1
A pseudorandom state generator or PRS(respectively, pseudorandom function-like state generator or PRFS) is the same as \(\textsf {PRSPD}\) (respectively, PRFSPD), but without the  and
and  algorithms, and the correctness and \(\mathsf {Unforgeability\text {-}of\text {-}proofs}\) requirements.
algorithms, and the correctness and \(\mathsf {Unforgeability\text {-}of\text {-}proofs}\) requirements.
Remark 2
(\({{\textsf {\textit{PRFSPD}}}}\) Input Shortening and \({{\textsf {\textit{PRSPD}}}}\)). \(\textsf {PRFSPD}\) with input length d immediately implies \(\textsf {PRFSPD}\) with input length \(d' \in \{ 0, 1, \cdots , d \}\) and in particular \(\textsf {PRSPD}\). To see this, if  is a \(\textsf {PRFSPD}\) with input length d, then for any \(d' \in \{ 0, 1, \cdots , d \}\), consider the \(d'\)-input-length scheme
is a \(\textsf {PRFSPD}\) with input length d, then for any \(d' \in \{ 0, 1, \cdots , d \}\), consider the \(d'\)-input-length scheme  where for \(x' \in \{ 0, 1 \}^{d'}\):
where for \(x' \in \{ 0, 1 \}^{d'}\):
-
 .
. -
 .
.
This is similar to how pseudorandom function-like states imply pseudorandom states: A reduction that takes an adversary against the new scheme and attaches \(d - d'\) zeros to its queries shows that we can use it in order to break the original scheme. Finally, \(\textsf {PRFSPD}\) with input length 0 exactly implies the definition of a \(\textsf {PRSPD}\).
Remark 3
(Computational assumptions are necessary for \({{\textsf {\textit{PRSPD}}}}\) and \({{\textsf {\textit{PRFSPD}}}}\)). Clearly, \(\textsf {PRSPD}\) with \(\omega (\log (1^\lambda ))\) output-length implies \(\textsf {PRS}\) with \(\omega (\log (1^\lambda ))\) output-length which cannot exist unconditionally [2, 17], hence \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\) with \(\omega (\log (1^\lambda ))\) output-length cannot exist unconditionally. It should be noted that \(\textsf {PRSPD}\) (and therefore \(\textsf {PRFSPD}\)) with \(O(\log (1^\lambda ))\) cannot exist since an adversary can learn an approximate description of the \(\textsf {PRSPD}\) state efficiently using tomography and use this description to win the forging game, see Game 1.
3.2 Distributions Related to the  Algorithm of \(\textsf {PRSPD}\), \(\textsf {PRFSPD}\), and Haar Random States
Algorithm of \(\textsf {PRSPD}\), \(\textsf {PRFSPD}\), and Haar Random States
Definition 3
(Correlated and independent destructions for Haar random states). For any algorithm  , that take a n-qubit state as input and outputs a c-bit classical string as output, and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\),
, that take a n-qubit state as input and outputs a c-bit classical string as output, and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\),  is the distribution on \(\{0,1\}^{ct}\) given by,
is the distribution on \(\{0,1\}^{ct}\) given by,  where
where

For every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), let  be the t-fold product of
be the t-fold product of  which is given by
which is given by

Definition 4
(Correlated and independent destructions of \(\boldsymbol{\textsf{PRSPD}}\) and \(\boldsymbol{\textsf{PRFSPD}}\)). For any \(\textsf {PRSPD}\) family  and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), \(\textsf{Correlated}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) is the distribution on \(\{0,1\}^{ct}\) given by, \((f_1,\ldots ,f_t)\sim \textsf{Correlated}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) where
and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), \(\textsf{Correlated}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) is the distribution on \(\{0,1\}^{ct}\) given by, \((f_1,\ldots ,f_t)\sim \textsf{Correlated}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) where

For every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), let \(\textsf{Product}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) be the t-fold product of \(\textsf{Product}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} \) which is given by

For any \(\textsf {PRFSPD}\) family  , for any \(x\in \{0,1\}^d\) and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), let \(\textsf{Correlated}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD},x}_t=\textsf{Correlated}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD} _x}_t\) and \(\textsf{Product}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD},x}=\textsf{Product}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD} _x}\), where \(\mathcal {PRFSPD} _x\) is the \(\textsf {PRSPD}\) scheme obtained out of \(\mathcal {PRFSPD} \) by fixing the input to x, see Definition 2 and Remark 2.
, for any \(x\in \{0,1\}^d\) and for every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), let \(\textsf{Correlated}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD},x}_t=\textsf{Correlated}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD} _x}_t\) and \(\textsf{Product}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD},x}=\textsf{Product}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD} _x}\), where \(\mathcal {PRFSPD} _x\) is the \(\textsf {PRSPD}\) scheme obtained out of \(\mathcal {PRFSPD} \) by fixing the input to x, see Definition 2 and Remark 2.
3.3 Properties of Pseudorandom States and Function-Like States with Proofs of Destruction
In this section, we state a few properties of \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\), that would be important for the applications in Sect. 5. These properties (Lemmas 1–5) are true for arbitrary \(\textsf {PRSPD}\) and \(\textsf {PRFSPD}\), but due to space constraints, we only sketch the proofs in this version. For simplicity, some of the proofs are sketched only for a special case, where the  algorithm of the respective \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\) family measures the state in the computational basis, and outputs the measurement outcome. Note that the
algorithm of the respective \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\) family measures the state in the computational basis, and outputs the measurement outcome. Note that the  algorithm, in general, could be more complicated and involve ancillae registers. The proof for the general case is given in full version.
algorithm, in general, could be more complicated and involve ancillae registers. The proof for the general case is given in full version.
Lemma 1
(\(\boldsymbol{\textsf{PRSPD}}\) have well-distributed proofs). For every \(\textsf {PRSPD}\) scheme  with key length \(w(\lambda )\) proof length \(c(\lambda )\), for every \(a\in \{0,1\}^c\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }_a\),
with key length \(w(\lambda )\) proof length \(c(\lambda )\), for every \(a\in \{0,1\}^c\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }_a\),

Furthermore, there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}_a\), such that

Proof sketch for the special case
The proof follows by combining pseudorandomness of the \(\textsf {PRSPD}\) with the observation that the  algorithm on a
algorithm on a  random state produces a uniformly random outcome. \(\Box \)
random state produces a uniformly random outcome. \(\Box \)
The proof for the general case is given in the full version.
Lemma 2
(\(\boldsymbol{\textsf{PRSPD}}\) proofs are distributed close to product distribution). Let  be a \(\textsf {PRSPD}\) scheme with key length \(w(\lambda )\) proof length \(c(\lambda )\). For every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), and \( a_1,\ldots ,a_t\in \{0,1\}^c\),Footnote 5
be a \(\textsf {PRSPD}\) scheme with key length \(w(\lambda )\) proof length \(c(\lambda )\). For every \(t\in \textsf{poly}{\left( {\lambda }\right) }\), and \( a_1,\ldots ,a_t\in \{0,1\}^c\),Footnote 5

where the subscript in the probability denotes the distribution of \((f_1,\ldots ,f_t)\), and the distributions are as defined in Definition 3.
Proof sketch for the special case
Observe that for any \(a_1,\ldots ,a_t\in \{0,1\}^{c(\lambda )}\), there exists a unique \(\boldsymbol{z}\) such that \(\langle a_1,\ldots ,a_t \vert \text {Sym}^{\boldsymbol{z}}_t \rangle \) is non-zero, see Sect. 2 for the definition of \(\text {Sym}^{\boldsymbol{z}}_t\). Combining this observation with Eq. (6) and the fact that  is just a measurement in the computational basis, we conclude that
is just a measurement in the computational basis, we conclude that  , i.e.,
, i.e.,

where equality holds when \(a_1=\cdots =a_t\). Moreover,  for every \(a_1,\ldots ,a_t\in \{0,1\}^{c(\lambda )}\). Hence,
for every \(a_1,\ldots ,a_t\in \{0,1\}^{c(\lambda )}\). Hence,

\(\Box \)
The proof for the general case is given in the full version.
Remark 4
For every \(t\in \textsf{poly}{\left( {\lambda }\right) }\),  and
and  are efficiently samplable using a state t-design and a state 1-design for n-qubit quantum states, respectively.
are efficiently samplable using a state t-design and a state 1-design for n-qubit quantum states, respectively.
Lemma 3
(\(\boldsymbol{\textsf{PRSPD}}\) proofs are collision-free). For every \(\textsf {PRSPD}\) scheme  with key length \(w(\lambda )\), proof length \(c(\lambda )\), and \(t\in \textsf{poly}{\left( {\lambda }\right) }\), there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}\),
with key length \(w(\lambda )\), proof length \(c(\lambda )\), and \(t\in \textsf{poly}{\left( {\lambda }\right) }\), there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}\),
where the subscript under the probability is the distribution on \(f_1,\ldots ,f_t\) and \(\textsf{Correlated}\text {-}\textsf{Destruction} ^\mathcal {PRSPD} _t\) is as defined in Definition 4.
Moreover, by the pseudorandomness of \(\textsf {PRSPD}\) (see Definition 1) there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}\) such that

where  is as defined in Definition 3.
is as defined in Definition 3.
Proof sketch for the special case
The moreover part follows by observing that for any \(t\in \textrm{poly}\left( {n}\right) \), measuring t-copies of a n-qubit  random state, is statistically close up to negligible distance (in n) to the t-fold product of the uniform distribution on \(\{0,1\}^n\). Hence, the probability of observing indistinct t-outcomes is negligible. The rest of the proof follows due to the pseudorandomness of the \(\textsf {PRSPD}\). \(\Box \)
random state, is statistically close up to negligible distance (in n) to the t-fold product of the uniform distribution on \(\{0,1\}^n\). Hence, the probability of observing indistinct t-outcomes is negligible. The rest of the proof follows due to the pseudorandomness of the \(\textsf {PRSPD}\). \(\Box \)
The proof for the general case is given in the full version.
Lemma 4
(\(\boldsymbol{\textsf{PRFSPD}}\) proofs are collision-free). For every \(\textsf {PRFSPD}\) scheme  with key length \(w(\lambda )\), input length \(d(\lambda )\), proof length \(c(\lambda )\), and \(t\in \textsf{poly}{\left( {\lambda }\right) }\), and \(x\in \{0,1\}^d\) there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}\),
with key length \(w(\lambda )\), input length \(d(\lambda )\), proof length \(c(\lambda )\), and \(t\in \textsf{poly}{\left( {\lambda }\right) }\), and \(x\in \{0,1\}^d\) there exists a negligible function \(\widetilde{\textsf{negl}{\left( {\lambda }\right) }}\),
where \(\textsf{Correlated}\text {-}\textsf{Destruction} ^{\mathcal {PRFSPD},x}_t\) is as defined in Definition 4.
Proof
Given a \(\textsf {PRFSPD}\) scheme \(\mathcal {PRFSPD} \) with input length \(d(\lambda )\), and any fixed input \(x\in \{0,1\}^d\), we can construct a \(\textsf {PRSPD}\) scheme \(\mathcal {PRSPD} _x\) as per Remark 2. Applying Lemma 3 on \(\mathcal {PRSPD} _x\), we get the desired result.
Lemma 5
(Classical unforgeability of \(\boldsymbol{\textsf{PRFSPD}}\)). Let  be a Pseudorandom function-like state generator with proofs of destruction family. Then, for every \(\textsf {QPT}\) adversary \(\mathcal {A}\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that
be a Pseudorandom function-like state generator with proofs of destruction family. Then, for every \(\textsf {QPT}\) adversary \(\mathcal {A}\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that
where \(\textsf{Classical}\text {-}\textsf{Forging}\text {-}\textsf{Exp}^{\mathcal {A},\textsf {PRFSPD}}_{\lambda } \) is defined in Game 3.

Proof sketch
The proof follows by combining Lemma 4 with the \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) property of \(\textsf {PRFSPD}\). \(\Box \)
The proof for the general case is given in the full version.
4 Construction of \(\textsf {PRFSPD}\) from any Post-quantum One-Way Function
In this section, we construct \(\textsf {PRFSPD}\) (Definition 2) from post-quantum one-way functions. To be more precise, we build a \(\textsf {PRFSPD}\) from post-quantum pseudorandom permutations (\(\textsf {PRP}\)), and since post-quantum OWFs imply post-quantum PRPs [26], our statement follows. Finally, recall Remark 2 which explains why a PRFSPD with input length \(d(\lambda ) = \lambda \) implies a PRFSPD with input length \(0 \le d'(\lambda ) \le d(\lambda )\), which also means that it implies a PRSPD.
Theorem 2
(Main Theorem). Assume there exist post-quantum one-way functions. Then, a \(\textsf {PRFSPD}\) scheme (Definition 2) with key length \(w(\lambda ) = \lambda \), input length \(d(\lambda ) = \lambda \), output length \(n(\lambda ) = 5\cdot \lambda \) and proof length \(c(\lambda ) = 5\cdot \lambda \), exists.
The construction is given in Fig. 2 and Fig. 3. In the construction, as in the main theorem, we define the following lengths as a function of the security parameter: key length \(w(\lambda ) = \lambda \), input length \(d(\lambda ) = \lambda \), output length \(n(\lambda ) = 5\cdot \lambda \) and proof length \(c(\lambda ) = 5\cdot \lambda \). Our only cryptographic ingredient is a post-quantum pseudorandom permutation \(\textsf{PRP}\) on \(5\lambda \) bits.
We next prove the security of the \(\textsf {PRFSPD}\) construction. This means two things: That the generated states are pseudorandom and that the classical proofs generated are unforgeable. To this end, we prove our main technical lemma that will easily imply both security aspects. Roughly, the lemma below implies that (1) classical access to the  oracle, is computationally indistinguishable from an oracle that outputs truly random quantum states, and (2) for every input \(x \in \{ 0, 1 \}^{d}\), generating more proofs of destruction than the number of queries that were made to the
oracle, is computationally indistinguishable from an oracle that outputs truly random quantum states, and (2) for every input \(x \in \{ 0, 1 \}^{d}\), generating more proofs of destruction than the number of queries that were made to the  oracle for x is information theoretically impossible.
oracle for x is information theoretically impossible.
Lemma 6
(Main Technical Lemma). Let T a polynomial and let \(\mathcal {A}\) a quantum polynomial-time algorithm that outputs a bit \(b \in \{ 0, 1 \}\) and has classical oracle access to some arbitrary oracle with inputs in \(\{0,1\}^{d}\), such that for every possible input \(x \in \{ 0, 1 \}^{d}\), \(\mathcal {A}\) makes either 0 or exactly T queries to the oracle on that input x. Then the following two distributions on b are computationally indistinguishable:
-
\(D_0:\) Sample \(k \leftarrow \{ 0, 1 \}^{\lambda }\) uniformly at random. \(\mathcal {A}\) has classical access to
 ,
,  (from Fig. 2 and Fig. 3, respectively), and makes either 0 or exactly T queries to each of the possible inputs \(x \in \{0,1\}^{d}\) to
(from Fig. 2 and Fig. 3, respectively), and makes either 0 or exactly T queries to each of the possible inputs \(x \in \{0,1\}^{d}\) to  , and outputs a bit b.
, and outputs a bit b. -
\(D_1:\) For every \(x \in \{ 0, 1 \}^{d}\), sample a T-sized multi-set of \(\{ 0, 1 \}^{5\lambda }\): \(\left( a_{x, 1}, \cdots , a_{x, T} \right) \), and generate the \(T \cdot 5\lambda \)-qubit state,
$$ \vert \pi _x \rangle := \sum _{\sigma \in S_{T}}\vert a_{x, \sigma (1)}, \cdots , a_{x, \sigma (T)} \rangle , $$and for each \(x \in \{ 0, 1 \}^{d}\), partition the \(T \cdot 5\lambda \)-qubit state \(\vert \pi _x \rangle \) into T sub-registers, each of size \(5\lambda \). The oracles are defined as follows: The generation oracle
 , given \(x \in \{ 0, 1 \}^{d}\) for the c-th query (for \(c \in [T]\)), outputs the c-th sub-register of the state \(\vert \pi _x \rangle \). The proof verification oracle
, given \(x \in \{ 0, 1 \}^{d}\) for the c-th query (for \(c \in [T]\)), outputs the c-th sub-register of the state \(\vert \pi _x \rangle \). The proof verification oracle  , given query \((x, q) \in \left( \{ 0, 1 \}^{d} \times \{ 0, 1 \}^{5\lambda } \right) \), outputs 1 iff \(q \in \{ a_{x, 1}, \cdots , a_{x, T} \}\). \(\mathcal {A}\) has classical access to
, given query \((x, q) \in \left( \{ 0, 1 \}^{d} \times \{ 0, 1 \}^{5\lambda } \right) \), outputs 1 iff \(q \in \{ a_{x, 1}, \cdots , a_{x, T} \}\). \(\mathcal {A}\) has classical access to 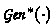 ,
,  , makes either 0 or exactly T queries to
, makes either 0 or exactly T queries to  for every \(x \in \{ 0, 1 \}^{d}\), and outputs a bit b.
for every \(x \in \{ 0, 1 \}^{d}\), and outputs a bit b.
The proof of the lemma is deferred to the full version.
Proposition 1
(Security - Pseudorandomness). The \(\textsf {PRFSPD}\) scheme in Fig. 2, Fig. 3 maintains the pseudorandomness property (as in Definition 2).
Proof
Let \(\mathcal {A}\) be a quantum polynomial-time adversary and let T be a polynomial bound on the running time of \(\mathcal {A}\). We claim that one can assume without the loss of generality that for every possible input \(x \in \{ 0, 1 \}^{d}\), \(\mathcal {A}\) makes either 0 or exactly T queries to the generation oracle  oracle. The reason is as follows: We can think of a new adversary \(\mathcal {A}'\) that, at the end of the execution of \(\mathcal {A}\), takes the inputs in \(\{ 0, 1 \}^{d}\) that \(\mathcal {A}\) queried during its execution \(x_1, \cdots , x_t \in \{ 0, 1 \}^{d}\) (for \(t \in [T]\)) without considering multiplicity (i.e., some of the inputs were possibly queried more than others) and for each of these inputs, complementing the number of times that it was queried (which, as we know is bounded by T by the fact that T is an upper bound on the total running time of \(\mathcal {A}\)) to be T - such adversary still breaks the pseudorandomness security guarantee and also satisfies the property that for every possible input in \(\{ 0,1 \}^{d}\), the input was queried either 0 or T times. Now, Lemma 6 in particular says that the output of \(\mathcal {A}\) on the classical access to the generation function
oracle. The reason is as follows: We can think of a new adversary \(\mathcal {A}'\) that, at the end of the execution of \(\mathcal {A}\), takes the inputs in \(\{ 0, 1 \}^{d}\) that \(\mathcal {A}\) queried during its execution \(x_1, \cdots , x_t \in \{ 0, 1 \}^{d}\) (for \(t \in [T]\)) without considering multiplicity (i.e., some of the inputs were possibly queried more than others) and for each of these inputs, complementing the number of times that it was queried (which, as we know is bounded by T by the fact that T is an upper bound on the total running time of \(\mathcal {A}\)) to be T - such adversary still breaks the pseudorandomness security guarantee and also satisfies the property that for every possible input in \(\{ 0,1 \}^{d}\), the input was queried either 0 or T times. Now, Lemma 6 in particular says that the output of \(\mathcal {A}\) on the classical access to the generation function  (which is part of \(D_0\) in the lemma’s statement) is computationally indistinguishable from the output of \(\mathcal {A}\) when the access is to the generation function
(which is part of \(D_0\) in the lemma’s statement) is computationally indistinguishable from the output of \(\mathcal {A}\) when the access is to the generation function  defined in the distribution \(D_1\), in the statement of the Lemma 6.
defined in the distribution \(D_1\), in the statement of the Lemma 6.
One of the standard facts in quantum information theory is that the distribution generated by T copies of a truly random, \(5\lambda \)-qubit Haar state is statistically equivalent (i.e. has trace distance 0) to the projection onto the \((5\lambda , T)\)-symmetric subspace ([15, Prop. 6]). In turn, an orthonormal basis for the \((5\lambda , T)\)-symmetric subspace is given by the set of states defined by all T-sized multi-sets of \(\{ 0, 1 \}^{5\lambda }\): For each T-sized multi-set M of \(\{ 0, 1 \}^{5\lambda }\), the corresponding state \(\vert \psi _M \rangle \) is a \(5\lambda \cdot T\)-qubit state which is the uniform superposition over all of the possible permutations of the T elements of M (e.g. in case M is not only a multi-set but an actual T-sized set, and all of its elements are distinct, the number of such permutations is T!, and if M is T times the same element, the number of such permutations is 1).
It follows that the projection onto the \((5\lambda , T)\)-symmetric subspace is exactly the mixed state that corresponds to the distribution induced by sampling a T-sized multi-set M of \(\{ 0, 1 \}^{5\lambda }\) and outputting the quantum state \(\vert \psi _M \rangle \). To conclude, for T queries, the oracle access  is equivalent to the oracle that outputs T copies of a \(5\lambda \)-qubit Haar random state, and since the output bit of \(\mathcal {A}\) is indistinguishable between
is equivalent to the oracle that outputs T copies of a \(5\lambda \)-qubit Haar random state, and since the output bit of \(\mathcal {A}\) is indistinguishable between  and
and  , then the output bit of \(\mathcal {A}\) is also indistinguishable between
, then the output bit of \(\mathcal {A}\) is also indistinguishable between  and an oracle that outputs Haar random states, in contradiction to the assumption that \(\mathcal {A}\) breaks the pseudorandomness guarantee. \(\Box \)
and an oracle that outputs Haar random states, in contradiction to the assumption that \(\mathcal {A}\) breaks the pseudorandomness guarantee. \(\Box \)
Proposition 2
(Security - Unforgeability of Proofs). The \(\textsf {PRFSPD}\) scheme in Fig. 2 and Fig. 3 maintains the Unforgeability-of-proofs property (as in Definition 2).
Proof
Assume toward contradiction there exists a quantum polynomial-time adversary \(\mathcal {A}\) that breaks the proof-unforgeability property of the scheme, let \(\varepsilon \) the probability that the adversary obtains in winning the forging game (i.e. \(\varepsilon \) is non-negligible). If T is a polynomial bound on the running time of \(\mathcal {A}\), note that we can assume without the loss of generality that for every possible input \(x \in \{ 0, 1 \}^{d}\), \(\mathcal {A}\) makes either 0 or exactly T queries to the generation oracle  and arbitrarily many queries to the verification oracle
and arbitrarily many queries to the verification oracle  (in the boundaries of its running time). The reason this can be assumed w.l.o.g. is because we can consider a new adversary \(\mathcal {A}'\) that uses \(\mathcal {A}\) and (similarly to how we defined \(\mathcal {A}'\) as a function of \(\mathcal {A}\) in the proof of Proposition 1) complements the number of queries for each of its \(t \in [T]\) previously-queried x’s to being queried T times. However, this argument is a bit more delicate when it comes to showing how the new adversary \(\mathcal {A}'\) breaks the proof-unforgeability property: At the end of the execution of the inner adversary \(\mathcal {A}\), it outputs \(x, p_1, \cdots , p_{t_x + 1}\) (where \(t_x\) is the number of times that the input \(x \in \{ 0, 1 \}^{d}\) was queried to
(in the boundaries of its running time). The reason this can be assumed w.l.o.g. is because we can consider a new adversary \(\mathcal {A}'\) that uses \(\mathcal {A}\) and (similarly to how we defined \(\mathcal {A}'\) as a function of \(\mathcal {A}\) in the proof of Proposition 1) complements the number of queries for each of its \(t \in [T]\) previously-queried x’s to being queried T times. However, this argument is a bit more delicate when it comes to showing how the new adversary \(\mathcal {A}'\) breaks the proof-unforgeability property: At the end of the execution of the inner adversary \(\mathcal {A}\), it outputs \(x, p_1, \cdots , p_{t_x + 1}\) (where \(t_x\) is the number of times that the input \(x \in \{ 0, 1 \}^{d}\) was queried to  by the inner adversary \(\mathcal {A}\)) such that
by the inner adversary \(\mathcal {A}\)) such that  . The outer adversary \(\mathcal {A}'\) then takes the extra \(\ell := T - t_x\) queries that it made (these are the queries it made in order to complement the number of queries for x from \(t_x\) to T, as part of the transformation of the inner adversary \(\mathcal {A}\) to the outer adversary \(\mathcal {A}'\)) for the input string x and measures the \(\ell \) copies it got in the computational basis, to obtain \(\ell \) valid classical proofs of destruction for x.
. The outer adversary \(\mathcal {A}'\) then takes the extra \(\ell := T - t_x\) queries that it made (these are the queries it made in order to complement the number of queries for x from \(t_x\) to T, as part of the transformation of the inner adversary \(\mathcal {A}\) to the outer adversary \(\mathcal {A}'\)) for the input string x and measures the \(\ell \) copies it got in the computational basis, to obtain \(\ell \) valid classical proofs of destruction for x.
Note that each of the \(\ell \) copies is a uniform superposition over a set of size \(2^\lambda \), which means that the probability that any of the \(\ell \) (which is a polynomial because T is a polynomial) proofs collides with the \(t_x + 1\) proofs generated by the cheating inner adversary \(\mathcal {A}\), is negligible. Thus, the new outer adversary \(\mathcal {A}'\) makes a total of T queries on the input \(x \in \{ 0, 1 \}^{d}\) but manages to generate \(T + 1\) distinct classical proofs of destruction, which means it breaks the security with a non-negligible probability \(\varepsilon '\). Finally, one can think of an even outer process \(\mathcal {A}^*\), that uses \(\mathcal {A}'\) to generate the \(T + 1\) proofs, then checks by itself their validity using the verification algorithm  , and outputs a bit whether or not the adversary \(\mathcal {A}'\) won the forging game. Note that because \(\mathcal {A}'\) wins the forging game with the non-negligible probability \(\varepsilon '\), then with the same probability, the output bit of \(\mathcal {A}^{*}\) is 1.
, and outputs a bit whether or not the adversary \(\mathcal {A}'\) won the forging game. Note that because \(\mathcal {A}'\) wins the forging game with the non-negligible probability \(\varepsilon '\), then with the same probability, the output bit of \(\mathcal {A}^{*}\) is 1.
Finally, by Lemma 6, it follows that the output bit of \(\mathcal {A}^*\) in the above process is computationally indistinguishable from its output bit in the setting \(D_1\) defined in Lemma 6, where \(\mathcal {A}^*\) gets access only to  and
and  (rather than
(rather than  and
and  ). Now, given the access to the two oracles
). Now, given the access to the two oracles  and
and  (i.e., in the setting of \(D_1\)), for any algorithm, even unbounded, the probability to output \(T + 1\) distinct strings that are all verified by the algorithm
(i.e., in the setting of \(D_1\)), for any algorithm, even unbounded, the probability to output \(T + 1\) distinct strings that are all verified by the algorithm  for some \(x \in \{ 0, 1 \}^{d}\) is zero, as by its definition, accepts at most T different elements. Our contradiction follows from the fact that \(\varepsilon '\) (the probability for \(\mathcal {A}^{*}\) to output 1 in the setting \(D_0\)) is non-negligible, but has to be negligibly close to 0 (the probability for \(\mathcal {A}^{*}\) to output 1 in the setting \(D_1\), where it has access only to the oracles
for some \(x \in \{ 0, 1 \}^{d}\) is zero, as by its definition, accepts at most T different elements. Our contradiction follows from the fact that \(\varepsilon '\) (the probability for \(\mathcal {A}^{*}\) to output 1 in the setting \(D_0\)) is non-negligible, but has to be negligibly close to 0 (the probability for \(\mathcal {A}^{*}\) to output 1 in the setting \(D_1\), where it has access only to the oracles  and
and  ). \(\Box \)
). \(\Box \)
5 Applications: Cryptography with Classical Communication
In this section, all the constructions of the cryptographic primitives are fully black-box constructions with uniform security reductions [22] from either \(\textsf {PRSPD}\) or \(\textsf {PRFSPD}\), except for the construction of the statistically binding and computationally hiding bit-commitment scheme given in the full version, which is a fully black-box (with uniform reduction) construction from the particular class of \(\textsf {PRSPD}\) that satisfies some special properties, see the full version for more details. Therefore, the security guarantees of all these primitives hold even against non-uniform adversaries with quantum advice, assuming the same notion of security for the underlying \(\textsf {PRSPD}\) (or a special form of it) and \(\textsf {PRFSPD}\). For simplicity, we only consider uniform adversaries from here onwards. Moreover, the outputs of all the algorithms in these constructions should be considered classical unless explicitly specified otherwise. Due to space constraints, some of the results and proofs have been moved to the full version.
None of the cryptographic primitives considered in the applications can exist unconditionally; see the full version for more details.
5.1 CMA-Secure MAC
Definition 5
(Length-restricted strong \(\textsf{CMA}\)-secure \(\textsf{MAC}\) (Adapted from [14, Definition 6.2.1])). A \(\text {length-restricted }\textsf{CMA}\text { secure }\textsf{MAC} \) scheme (\(\mathcal {M} \)) with message length \(d(\lambda )\)Footnote 6, key-length \(w(\lambda )\), and tag-length \(c(\lambda )\) is a tuple of \(\textsf {QPT}\) algorithms  with the following syntax:
with the following syntax:
-
 : takes a key \(k\in \{0,1\}^{w(\lambda )}\), a message \(m\in \{0,1\}^{d(\lambda )}\), and outputs a tag \(\textsf{sig} \in \{0,1\}^c\).
: takes a key \(k\in \{0,1\}^{w(\lambda )}\), a message \(m\in \{0,1\}^{d(\lambda )}\), and outputs a tag \(\textsf{sig} \in \{0,1\}^c\). -
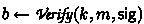 : takes a key k, a message m, a tag \(\textsf{sig} \), and outputs a boolean value, either accept (\(b=1\)) or reject (\(b=0\)).
: takes a key k, a message m, a tag \(\textsf{sig} \), and outputs a boolean value, either accept (\(b=1\)) or reject (\(b=0\)).
Correctness. For every message \(m\in \{0,1\}^{d(\lambda )}\),

Strong \(\textsf{CMA}\) Unforgeability. For every \(\textsf {QPT}\) adversary \(\mathcal {A}\) in the forging game (see Game 4), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that

Remark 5
(Strong vs. vanilla \(\textsf{CMA} \) security). Vanilla \(\textsf{CMA} \) security considers a similar forging game in which the adversary wins if she produces \((m,\sigma )\) that passes verification and that m was never queried to the  oracle. In comparison, Definition 5 is a stronger notion because the adversary wins the forging game even if she produces a valid \((m,\sigma )\) such that m was queried to the
oracle. In comparison, Definition 5 is a stronger notion because the adversary wins the forging game even if she produces a valid \((m,\sigma )\) such that m was queried to the  oracle as long as \(\sigma \) was not received as a response in any of the m-queries she did to the
oracle as long as \(\sigma \) was not received as a response in any of the m-queries she did to the  oracle. Hence, we call this notion the strong \(\textsf{CMA} \) security, also referred to as super-secure \(\textsf{MAC} \)sFootnote 7 in [14, Sect. 6.5.2]. These notions are not known to be equivalent in general. However, the prominent classical \(\textsf{MAC} \) constructions have deterministic signing procedures, i.e., every message has a unique signature string that passes verification, and all other strings are rejected. For such \(\textsf{MAC} \) schemes, strong and vanilla \(\textsf{CMA} \) security are equivalent. This is not the case for our construction. Hence we consider the strongest possible definition.
oracle. Hence, we call this notion the strong \(\textsf{CMA} \) security, also referred to as super-secure \(\textsf{MAC} \)sFootnote 7 in [14, Sect. 6.5.2]. These notions are not known to be equivalent in general. However, the prominent classical \(\textsf{MAC} \) constructions have deterministic signing procedures, i.e., every message has a unique signature string that passes verification, and all other strings are rejected. For such \(\textsf{MAC} \) schemes, strong and vanilla \(\textsf{CMA} \) security are equivalent. This is not the case for our construction. Hence we consider the strongest possible definition.
Remark 6
(Access to the verification oracle). In the classical \(\textsf{CMA} \) security definitions, the adversary is not given access to the verification because the classical \(\textsf{MAC} \) schemes usually have deterministic signing procedures; hence the verification oracle can be simulated using the signing oracle, see [14, Proposition 6.1.3]. However, \(\textsf{MAC} \) schemes with quantum algorithms do not have a deterministic signing in general; hence, we provide the adversary in \(\mathsf {Strong\text {-}CMA\text {-}Forging}\text {-}\textsf{Exp}^{\mathcal {A},\mathcal {M}}_{\lambda } \) explicit access to the verification oracle.
Construction from PRFSPD. Next we construct a \(\text {length-restricted }\textsf{CMA}\text { secure }\textsf{MAC}\) scheme with input-length \(d(\lambda )\), key-length \(w(\lambda )\) and tag-length \(c(\lambda )\) from a \(\textsf {PRFSPD}\) scheme  with key-length \(w(\lambda )\), input-length \(d(\lambda )\) and proof-length \(c(\lambda )\). The construction given in Fig. 4, combines the quantum \(\textsf{MAC} \) construction in [4] with the proof of destruction property of \(\textsf {PRFSPD}\), to get an improved construction in the following two aspects. Firstly, the tags in our construction are classical, whereas [4] requires quantum tags. Additionally, our construction satisfies strong-\(\textsf{CMA} \) security while [4] considers vanilla \(\textsf{CMA} \) security. We also briefly mention that our construction supports any poly-size message, whereas the one in [4] is length-restricted. We note that we remove this length restriction using a standard technique, which is applicable to their construction as well.
with key-length \(w(\lambda )\), input-length \(d(\lambda )\) and proof-length \(c(\lambda )\). The construction given in Fig. 4, combines the quantum \(\textsf{MAC} \) construction in [4] with the proof of destruction property of \(\textsf {PRFSPD}\), to get an improved construction in the following two aspects. Firstly, the tags in our construction are classical, whereas [4] requires quantum tags. Additionally, our construction satisfies strong-\(\textsf{CMA} \) security while [4] considers vanilla \(\textsf{CMA} \) security. We also briefly mention that our construction supports any poly-size message, whereas the one in [4] is length-restricted. We note that we remove this length restriction using a standard technique, which is applicable to their construction as well.
Theorem 3
(Correctness of \(\mathcal {M}\) ). The length-restricted \(\textsf{MAC} \) scheme \(\mathcal {M} \) is correct (see Definition 5) if  satisfies correctness (see Definition 2).
satisfies correctness (see Definition 2).
The proof is immediate from the correctness of the proof of destruction of the underlying \(\textsf {PRFSPD}\), and hence we omit the proof.
Theorem 4
(CMA Security of \(\mathcal {M}\) ). The length-restricted \(\textsf{MAC} \) scheme \(\mathcal {M} \) is \(\textsf{CMA} \)-secure if  is a \(\textsf {PRFSPD}\) (see Definition 1).
is a \(\textsf {PRFSPD}\) (see Definition 1).
Proof
The proof directly follows from the classical-unforgeability of proofs for \(\textsf {PRFSPD}\) given in Lemma 5. \(\Box \)
Remark 7
(Unrestricted \(\textsf{MAC} \)). Note that the input-length of the \(\textsf{MAC} \), \(d(\lambda )\in \omega (\log (\lambda ))\). Hence, we can extend the \(\textsf{MAC} \) scheme to sign messages of arbitrary polynomial length by dividing the message into blocks and signing them individually; see [14, Theorem 6.2.2] for more details. Therefore, we conclude that \(\textsf {PRFSPD}\) implies \(\textsf{CMA} \) \(\textsf{MAC} \), in a black-box manner.
5.2 CPA-Secure Symmetric Encryption
In this section, we will construct \(\textsf{CPA} \)-secure symmetric bit-encryption from \(\textsf {PRFSPD}\), which can be easily extended to a \(\textsf{CPA} \)-secure and even \(\textsf{CCA}\)-2 encryption for arbitrary message-length, see Remarks 8 and 9.
Definition 6
(\(\textsf{CPA} \)-secure symmetric bit-encryption(Adapted from [14, Definition 5.4.9])). A \(\textsf{CPA}\text { secure symmetric bit-encryption} \) \(\mathcal {E} \) with key space \(\{0,1\}^{w(\lambda )}\), and cipher space \(\{0,1\}^{c(\lambda )}\) is a tuple of \(\textsf {QPT}\) algorithms  with the following syntax:
with the following syntax:
-
 : takes a key k and a message bit m, and outputs a classical cipher text \(\textsf{ct} \).
: takes a key k and a message bit m, and outputs a classical cipher text \(\textsf{ct} \). -
 : takes a key k, a cipher text \(\textsf{ct} \), and outputs a message bit m.
: takes a key k, a cipher text \(\textsf{ct} \), and outputs a message bit m.
Correctness: For every message \(m\in \{0,1\}\), there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\), such that

\(\textsf{CPA} \) security For every \(\textsf {QPT}\) adversary \(\mathcal {A}\) in the distinguishability game (see Game 5, there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that

Construction from PRFSPD. Let  be a \(\textsf {PRFSPD}\) with input length \(d(\lambda )\in \omega (\log (\lambda ))\), and key-length \(w(\lambda )\). We will give a construction of \(\textsf{CPA}\text { secure symmetric bit-encryption} \) from such a \(\textsf {PRFSPD}\) with key-length \(w(\lambda )\).
be a \(\textsf {PRFSPD}\) with input length \(d(\lambda )\in \omega (\log (\lambda ))\), and key-length \(w(\lambda )\). We will give a construction of \(\textsf{CPA}\text { secure symmetric bit-encryption} \) from such a \(\textsf {PRFSPD}\) with key-length \(w(\lambda )\).
In a nutshell, our construction combines the ideas in [4], with the proof of destruction property of \(\textsf {PRFSPD}\) state, to make the ciphers classical. The construction is given in Fig. 5.
Proposition 3
(Correctness of \(\mathcal {E}\) ). The symmetric bit-encryption scheme \(\mathcal {E} \) is correct (see Definition 6) if  satisfies correctness (see Definition 2).
satisfies correctness (see Definition 2).
Proof
By the correctness of the underlying \(\textsf {PRFSPD}\), the correctness holds for encryptions of 1, i.e.,

Next for encryptions of 0, it suffices to show that there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that,

The last equation can be proven using the \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) property of the underlying \(\textsf {PRFSPD}\) as follows. We construct an adversary \(\mathcal {A}\) in the cloning game \(\textsf{Forging}\text {-}\textsf{Exp}^{\mathcal {A},\textsf {PRFSPD}}_{\lambda } \) (see Game 2) that samples \(r_0\xleftarrow {u}\{0,1\}^{d-1} \) and queries the  oracle at \(r_0\Vert 1\) and gets a state \(\vert \psi ^{r_0\Vert 0} \rangle \). \(\mathcal {A}\) runs
oracle at \(r_0\Vert 1\) and gets a state \(\vert \psi ^{r_0\Vert 0} \rangle \). \(\mathcal {A}\) runs  on \(\vert \psi ^{r_0\Vert 0} \rangle \) to get a proof
on \(\vert \psi ^{r_0\Vert 0} \rangle \) to get a proof  , and finally submits \(r\Vert 0,p\). Note that \(\mathcal {A}\) never queried \(r\Vert 0\) to
, and finally submits \(r\Vert 0,p\). Note that \(\mathcal {A}\) never queried \(r\Vert 0\) to  before, so she wins the cloning game if \(r\Vert 0,p\) passes the \(\textsf {PRFSPD}\) verification which by design, happens with probability exactly \(\textsf{prob} _0\). Hence by the \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) property of \(\textsf {PRFSPD}\), \(\textsf{prob} _0\) must be negligible. \(\Box \)
before, so she wins the cloning game if \(r\Vert 0,p\) passes the \(\textsf {PRFSPD}\) verification which by design, happens with probability exactly \(\textsf{prob} _0\). Hence by the \(\mathsf {Unforgeability\text {-}of\text {-}proofs} \) property of \(\textsf {PRFSPD}\), \(\textsf{prob} _0\) must be negligible. \(\Box \)
Theorem 5
(CPA Security of \(\mathcal {E}\) ). The symmetric bit-encryption scheme \(\mathcal {E} \) is \(\textsf{CPA} \)-secure (see Definition 6) if  is a \(\textsf {PRFSPD}\) (see Definition 1).
is a \(\textsf {PRFSPD}\) (see Definition 1).
Proof
The proof follows essentially from the pseudorandomness of  (see Definition 2). We will consider the following sequence of hybrids:
(see Definition 2). We will consider the following sequence of hybrids:
\(\mathcal {H} _0\) This is the real security game \(\textsf{Distinguish}\text {-}\textsf{Exp}^{\mathcal {A},\mathcal {E}}_{\lambda } \). Since we are considering bit encryption, the challenger simply samples a bit b and feeds \(\mathcal {A}\) the encryption of b, i.e.,  at the challenge phase. The adversary \(\mathcal {A}\) is given classical access to the \(\textsf{CPA} \) oracle
at the challenge phase. The adversary \(\mathcal {A}\) is given classical access to the \(\textsf{CPA} \) oracle  which she can query both before and after the challenge phase. Let \(b_1,\ldots ,b_q\) be the queries \(\mathcal {A}\) makes to the \(\textsf{CPA} \) oracle where \(q\in \textsf{poly}{\left( {\lambda }\right) }\) (since \(\mathcal {A}\) is polynomially bounded), and
which she can query both before and after the challenge phase. Let \(b_1,\ldots ,b_q\) be the queries \(\mathcal {A}\) makes to the \(\textsf{CPA} \) oracle where \(q\in \textsf{poly}{\left( {\lambda }\right) }\) (since \(\mathcal {A}\) is polynomially bounded), and

be the respective responses from the oracle, where \(r_1,\ldots ,r_q\) are chosen uniformly. \(\mathcal {A}\) succeeds if she submits a bit \(b'\) at the end, such that \(b=b'\).
\(\mathcal {H} _1\) In this hybrid, we only change the distribution on \(r,r_1,\ldots ,r_q\). The challenger samples r independently, and then for every \(i\in [q]\), \(r_i\) is chosen uniformly from \(\{0,1\}^{d(\lambda )-1}\setminus \{r,r_1,\ldots ,r_{i-1}\}\), where \(\{r,r_1,\ldots ,r_{i-1}\}\) should be interpreted as \(\{r\}\) for \(i=1\). Note that the distributions on \((r,r_1,\ldots ,r_q)\) in the hybrid have negligible statistical distance from the uniformly random distribution that we had in \(\mathcal {H} _0\) because \(q\in \textsf{poly}{\left( {\lambda }\right) }\) and the length of r is \(d(\lambda )-1\in \omega (\log \lambda )\). Hence, the success probability of \(\mathcal {A}\) in \(\mathcal {H} _0\) and \(\mathcal {H} _1\) are negligibly close.
\(\mathcal {H} _2\) In this hybrid, we replace
 with
with
 where \(\vert \phi \rangle \sim \mu _{\mathcal {H}_n}\) and for each \(i\in [q]\), \(\vert \phi _i \rangle \sim \mu _{\mathcal {H}_n}\) independently.
where \(\vert \phi \rangle \sim \mu _{\mathcal {H}_n}\) and for each \(i\in [q]\), \(\vert \phi _i \rangle \sim \mu _{\mathcal {H}_n}\) independently.
Let the difference in the success probabilities of the \(\mathcal {A}\) in \(\mathcal {H} _1\) and \(\mathcal {H} _2\) be p. We can construct an adversary \(\mathcal {B}\) who can violate the pseudorandomness (see Definition 2) of  with distinguishing advantage p. \(\mathcal {B}\) simulates \(\mathcal {A}\) and when she queries \(b_i\) in the \(i^{th}\) query, \(\mathcal {B}\) generates \(r_i\) uniformly from \(\{0,1\}^{d(\lambda )-1}\setminus {r_1,\ldots ,r_{i-1}}\), and queries the oracle (which she needs to distinguish) on \(r_i\Vert b_i\) and performs
with distinguishing advantage p. \(\mathcal {B}\) simulates \(\mathcal {A}\) and when she queries \(b_i\) in the \(i^{th}\) query, \(\mathcal {B}\) generates \(r_i\) uniformly from \(\{0,1\}^{d(\lambda )-1}\setminus {r_1,\ldots ,r_{i-1}}\), and queries the oracle (which she needs to distinguish) on \(r_i\Vert b_i\) and performs  on the output she receives and feeds the obtained string to \(\mathcal {A}\). Moreover, \(\mathcal {B}\) plays the role of the challenger and samples a uniformly random bit b, and feeds the encryption of b using the challenge oracle that she has access to. \(\mathcal {B}\) outputs 1 if the output of the \(\mathcal {A}\) is the same as b. Clearly, the distinguishing probability is p. Hence, p must be negligible.
on the output she receives and feeds the obtained string to \(\mathcal {A}\). Moreover, \(\mathcal {B}\) plays the role of the challenger and samples a uniformly random bit b, and feeds the encryption of b using the challenge oracle that she has access to. \(\mathcal {B}\) outputs 1 if the output of the \(\mathcal {A}\) is the same as b. Clearly, the distinguishing probability is p. Hence, p must be negligible.
Now note that in \(\mathcal {H} _2\), the challenge bit b is information-theoretically hidden from \(\mathcal {A}\). Therefore, her success probability in \(\mathcal {H} _2\) must be at most \(\frac{1}{2}\).
Hence, there exists a negligible function \(\textsf{negl}{\left( {\lambda }\right) }\) such that
\(\Box \)
Remark 8
(Encryption of arbitrarily long messages). Any \(\textsf{CPA} \)-secure bit encryption scheme can be extended to a \(\textsf{CPA} \)-secure encryption to arbitrarily long messages via bit-by-bit encryption, see [14, Sect. 5.3.2.2]. Hence, we conclude that there is a black-box construction of \(\textsf{CPA} \)-secure encryption for arbitrary message lengths, from \(\textsf {PRFSPD}\).
Remark 9
(CCA-2 security of \(\mathcal {E}\) ). By combining the strong \(\textsf{MAC} \) scheme from \(\textsf {PRFSPD}\) (see Theorems 3 and 4) with the \(\textsf{CPA} \)-secure encryption scheme mentioned in the previous remark using the Encrypt-then-\(\textsf{MAC}\), we conclude that there is a black-box construction of CCA-2 secure encryption for arbitrarily long messages from PRFSPD.
Notes
- 1.
In this primitive, the verification is quantum, but sending the proof of possession to the verifier only requires classical communication.
- 2.
One may be concerned that true random states are infeasible to generate, however for our purposes here we can use so-called “state-designs” instead of true random states.
- 3.
For technical reasons which are outside the scope of this work, the algorithm can output abort.
- 4.
The pseudorandom security guarantee implies that with overwhelming probability over the chosen key, the state should be negligibly close to a pure state in trace distance; otherwise, pseudorandomness of the state can be violated via Swap-test.
- 5.
We believe that the distributions are in fact, statistically close due to the strong concentration of the Haar measure, but we have not been able to prove it. The lemma is a weaker version of this statement, but it suffices for our purposes.
- 6.
This is referred to as d-restricted \(\textsf{MAC} \) in [14].
- 7.
We use the term strong in place of super because strong is the more colloquially accepted term.
References
Amos, R., Georgiou, M., Kiayias, A., Zhandry, M.: One-shot signatures and applications to hybrid quantum/classical authentication. In: Makarychev, K., Makarychev, Y., Tulsiani, M., Kamath, G., Chuzhoy, J. (eds.) Proceedings of the Annual ACM SIGACT Symposium on Theory of Computing, pp. 255–268. ACM (2020). https://doi.org/10.1145/3357713.3384304
Ananth, P., Gulati, A., Qian, L., Yuen, H.: Pseudorandom (function-like) quantum state generators: new definitions and applications. In: Kiltz, E., Vaikuntanathan, V. (eds.) Theory of Cryptography, TCC 2022. LNCS, vol. 13747, pp. 237–265. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-22318-1_9
Ananth, P., Lin, Y., Yuen, H.: Pseudorandom strings from pseudorandom quantum states (2023)
Ananth, P., Qian, L., Yuen, H.: Cryptography from pseudorandom quantum states (2021)
Bartusek, J., Coladangelo, A., Khurana, D., Ma, F.: One-way functions imply secure computation in a quantum world. In: Malkin, T., Peikert, C. (eds.) Advances in Cryptology - CRYPTO 2021–41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, 16–20 August 2021, Proceedings, Part I. LNCS, vol. 12825, pp. 467–496. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84242-0_17
Behera, A., Sattath, O.: Almost public coins. In: QIP 2021 (2020)
Ben-David, S., Sattath, O.: Quantum tokens for digital signatures. QCrypt 2017 (2016). https://doi.org/10.48550/ARXIV.1609.09047
Bouland, A., Fefferman, B., Vazirani, U.V.: Computational pseudorandomness, the wormhole growth paradox, and constraints on the ADS/CFT duality (abstract). In: Vidick, T. (ed.) 11th Innovations in Theoretical Computer Science Conference, ITCS 2020, 12–14 January 2020, Seattle, Washington, USA. LIPIcs, vol. 151, pp. 63:1–63:2. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2020). https://doi.org/10.4230/LIPIcs.ITCS.2020.63
Brakerski, Z., Canetti, R., Qian, L.: On the computational hardness needed for quantum cryptography (2022)
Brakerski, Z., Shmueli, O.: (Pseudo) random quantum states with binary phase. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 229–250. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_10
Brakerski, Z., Shmueli, O.: Scalable pseudorandom quantum states. In: Micciancio, D., Ristenpart, T. (eds.) Advances in Cryptology - CRYPTO 2020–40th Annual International Cryptology Conference, CRYPTO 2020, Santa Barbara, CA, USA, 17–21 August 2020, Proceedings, Part II. LNCS, vol. 12171, pp. 417–440. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56880-1_15
Coladangelo, A., Liu, J., Liu, Q., Zhandry, M.: Hidden cosets and applications to unclonable cryptography. In: Malkin, T., Peikert, C. (eds.) Advances in Cryptology - CRYPTO 2021–41st Annual International Cryptology Conference, CRYPTO 2021, Virtual Event, 16–20 August 2021, Proceedings, Part I. LNCS, vol. 12825, pp. 556–584. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84242-0_20
Coladangelo, A., Sattath, O.: A quantum money solution to the blockchain scalability problem. Quantum 4, 297 (2020). https://doi.org/10.22331/q-2020-07-16-297
Goldreich, O.: The Foundations of Cryptography - Volume 2: Basic Applications. Cambridge University Press, Cambridge (2004). https://doi.org/10.1017/CBO9780511721656, http://www.wisdom.weizmann.ac.il/%7Eoded/foc-vol2.html
Harrow, A.W.: The church of the symmetric subspace (2013)
Ji, Z., Liu, Y., Song, F.: Pseudorandom quantum states. In: Shacham, H., Boldyreva, A. (eds.) Advances in Cryptology - CRYPTO 2018–38th Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2018, Proceedings, Part III. LNCS, vol. 10993, pp. 126–152. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_5
Kretschmer, W.: Quantum pseudorandomness and classical complexity. In: Hsieh, M. (ed.) 16th Conference on the Theory of Quantum Computation, Communication and Cryptography, TQC 2021, 5–8 July 2021, Virtual Conference. LIPIcs, vol. 197, pp. 2:1–2:20. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.TQC.2021.2
Molina, A., Vidick, T., Watrous, J.: Optimal counterfeiting attacks and generalizations for Wiesner’s quantum money. In: Iwama, K., Kawano, Y., Murao, M. (eds.) Theory of Quantum Computation, Communication, and Cryptography, TQC. LNCS, vol. 7582, pp. 45–64. Springer, Cham (2012). https://doi.org/10.1007/978-3-642-35656-8_4
Morimae, T., Yamakawa, T.: Quantum commitments and signatures without one-way functions. In: Dodis, Y., Shrimpton, T. (eds.) Advances in Cryptology - CRYPTO 2022–42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, 15–18 August 2022, Proceedings, Part I. LNCS, vol. 13507, pp. 269–295. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-15802-5_10
Morimae, T., Yamakawa, Y.: One-wayness in quantum cryptography, October 2022
Radian, R., Sattath, O.: Semi-quantum money. In: Proceedings of the 1st ACM Conference on Advances in Financial Technologies, AFT 2019, Zurich, Switzerland, 21–23 October 2019, pp. 132–146. ACM (2019). https://doi.org/10.1145/3318041.3355462
Reingold, O., Trevisan, L., Vadhan, S.P.: Notions of reducibility between cryptographic primitives. In: Naor, M. (ed.) TCC 2004, Cambridge, MA, USA Proceedings. LNCS, vol. 2951, pp. 1–20. Springer, Cham (2004). https://doi.org/10.1007/978-3-540-24638-1_1
Shmueli, O.: Public-key quantum money with a classical bank. In: Leonardi, S., Gupta, A. (eds.) STOC 2022: 54th Annual ACM SIGACT Symposium on Theory of Computing, Rome, Italy, 20–24 June 2022, pp. 790–803. ACM (2022). https://doi.org/10.1145/3519935.3519952
Shmueli, O.: Semi-quantum tokenized signatures. Cryptology ePrint Archive, Report 2022/228 (2022). https://ia.cr/2022/228
Zhandry, M.: How to construct quantum random functions. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS 2012, New Brunswick, NJ, USA, 20–23 October 2012, pp. 679–687. IEEE Computer Society (2012). https://doi.org/10.1109/FOCS.2012.37
Zhandry, M.: A note on quantum-secure PRPs (2016)
Zhandry, M.: Quantum lightning never strikes the same state twice. Or: quantum money from cryptographic assumptions. J. Cryptol. 34(1), 6 (2021)
Acknowledgments
Amit Behera and Or Sattath were supported by the Israeli Science Foundation (ISF) grant No. 682/18 and 2137/19, and by the Cyber Security Research Center at Ben-Gurion University. Zvika Brakerski is supported by the Israel Science Foundation (Grant No. 3426/21), and by the European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482). Omri Shmueli is supported by the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation programme (grant agreements No. 101042417, acronym SPP, and No. 756482, acronym REACT), by Israeli Science Foundation (ISF) grants 18/484 and 19/2137, by Len Blavatnik and the Blavatnik Family Foundation, and by the Clore Israel Foundation. The authors would like to thank the anonymous reviewers for their valuable and insightful comments.
 This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 756482).
This work has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 756482).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Behera, A., Brakerski, Z., Sattath, O., Shmueli, O. (2023). Pseudorandomness with Proof of Destruction and Applications. In: Rothblum, G., Wee, H. (eds) Theory of Cryptography. TCC 2023. Lecture Notes in Computer Science, vol 14372. Springer, Cham. https://doi.org/10.1007/978-3-031-48624-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-48624-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-48623-4
Online ISBN: 978-3-031-48624-1
eBook Packages: Computer ScienceComputer Science (R0)





 algorithm for general
algorithm for general  algorithm on the input state without measurement, then measure only the first
algorithm on the input state without measurement, then measure only the first  random, then the state on the unmeasured bits will be Haar random. However, the destruct algorithms may use ancillae qubits, and therefore the overall process becomes non-unitary, even before the measurement. Since non-unitary processes do not preserve
random, then the state on the unmeasured bits will be Haar random. However, the destruct algorithms may use ancillae qubits, and therefore the overall process becomes non-unitary, even before the measurement. Since non-unitary processes do not preserve  -random property, if we measure the first
-random property, if we measure the first  random.
random.
 : takes a key
: takes a key  : takes an
: takes an  : takes a key
: takes a key 
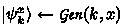 : takes a key
: takes a key  : takes an n-qubit quantum state
: takes an n-qubit quantum state  : takes a key
: takes a key 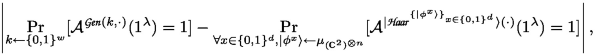
 outputs
outputs  represents that
represents that  .
.
 .
. .
. Algorithm of
Algorithm of 
 ,
,  (from Fig.
(from Fig.  , and outputs a bit b.
, and outputs a bit b. , given
, given  , given query
, given query  ,
,  , makes either 0 or exactly T queries to
, makes either 0 or exactly T queries to  for every
for every 
 : takes a key
: takes a key 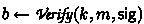 : takes a key k, a message m, a tag
: takes a key k, a message m, a tag 
 : takes a key k and a message bit m, and outputs a classical cipher text
: takes a key k and a message bit m, and outputs a classical cipher text  : takes a key k, a cipher text
: takes a key k, a cipher text 
