Keywords

1 Introduction

Due to the social and political movement towards sustainability, additive manufacturing of lightweight components is steadily moving closer to the industry’s focus. Currently, lightweight components, e.g. for aviation, are milled out of plate-material, converting up to 95% of the material into chips [1]. These are contaminated with cooling lubricants and show surface oxide layers, which makes recycling difficult and thus preventing a circular economy. Additive manufacturing offers the potential to reduce this waste by directly producing a near-net-shape semi-finished product. Only small allowances have to be removed from the component by machining operations.

However, the final machining of the near-net-shape semi-finished products poses new challenges for the manufacturing technology. The slender, thin-walled structures are prone to elastic deformation during machining, which remains as a dimensional surface error on the component. For manufacturing out of plate-material, methods, like the waterline-path approach have been developed, that utilize the residual stiffness of the solid-block to reinforce the surfaces to be machined. The surface error therefor results exclusively from the tool bending and has been extensively studied [10, 11]. For the finishing of additive, slender parts new solutions must be found. Various approaches have been tested in the past:

One way to reduce the elastic deformation and thus the surface error is to use less tool engagement [2], but since this limits the productivity, alternative approaches are preferable. Another approach is to reinforce the thin structures with fixtures [3]. However, these have the disadvantage of requiring assembly time, induce additional risk of collision and add extra cost. A different way to compensate the surface error is to adjust the tool path, e.g. by increasing the width of cut [4], or adjust the tool angle [5] to compensate for the bending line of the slender part. However, it has been noted [5, 6], that not every surface error can be compensated by adjusting the tool path. The characteristic of the surface error depends on the engagement conditions and the tool geometry. In addition, for additive parts, the slenderness of the component is expected to further influence the shape of the surface error. In order to find the ideal compensation strategy, an estimation of the resulting surface error is necessary so that a choice can be made between the different strategies. Typical approaches to predict the surface error use a combination of analytical force and numerical deformation calculation [6, 7, 9]. This method requires a time-consuming set up of the simulation, unknown cutting coefficients and are computation heavy, but offer the most accurate results. However, if the exact quantitative surface error is not needed, [5] provides an analytical prediction, that accelerates the calculation process significantly and needs less input parameters. The result can be used to pre-select tools and process parameters that lead to surface errors that are compensable by tool path adjustment. The quantitative amount of needed adjustment has to be gained another way, e.g. by online monitoring [8].

The aim of this paper is to provide a similar analytical qualitative surface error prediction that needs a minimal number of input parameters and provides fast calculation. The current model gets expanded to calculate not only the maximal, but the full shape of the qualitative surface error. The field of application gets enlarged for thin walls without a fixed clamping at the depth of cut and can thus be used for machining of near-net-shaped parts in multiple axial feeds, as required for additive parts. The results can get used to decide, whether an angular adjustment or increase in width of cut is suitable for surface error compensation.

2 Analytical Characterization of the Surface Error

With the assistance of an analytical model, it is possible to estimate the shape of the surface error without having to perform FE-simulations or experiments. With the help of a few parameters known to the NC-programmer, it is thus possible to predict the surface error and select a suitable tool, process parameters and compensation strategy in a computationally efficient manner. This makes the model attractive for industry.

2.1 Calculation Approach

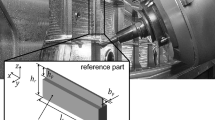
Due to the cutting forces at the contact lines between tooth and workpiece, forces generated during climb milling push workpiece and tool away from each other. Figure 1 (a) shows a flank milling process of a slender fillet that has a wall height \({\mathrm{h}}_{\mathrm{w}}\) below the depth of cut, which is typical for additive manufactured components. A typical surface error due to the displacement is shown in Fig. 1 (b). The error can be characterized via the following points:

  • Point A – Dimensional error at the highest depth of cut

  • Point B – Dimensional error at the lowest depth of cut

  • Point C – Maximum dimensional error

  • Point D – Minimum dimensional error

[4] introduces the Error-Linearity-Factor \(\zeta \) to describe the linearity of the dimensional error:

Fig. 1.
figure 1

(a) Flank milling of a thin walled part with resulting part deflection; (b) typical resulting surface error in the yx-plane

Full size image
Fig. 2.
figure 2

Uncoiled tool teeth and contact zone with the workpiece.

Full size image
$$\zeta =\frac{B-A}{C-A}.$$
(1)

A higher Linearity-Factor indicates a linear surface error, which can be compensated to a large extent by angular adjusting the toolpath. Manufacturing of slender parts results in surface errors, that can be compensated to an extend by increasing the width of cut. To describe, which fraction of the surface error can be compensated by increasing the width of cut, a new factor, the Error-Compensation-Factor \(\xi \), is introduced:

$$\xi =\frac{D}{C}.$$
(2)

To predict the qualitative surface error, derive the points A-D and Error-Factors an analytical approach is provided:

If the area of the tool that is in engagement is projected onto the uncoiled cutting profile, the cutting edge areas that are in engagement at a given time can be identified (see Fig. 2). Based on the geometric correlations, the required parameters for the analytical model can be calculated from known engagement and tool parameters:

2.2 Geometric Engagement Conditions

The contact angle \({\varphi }_{i}\) can be derived from the width of cut \({a}_{e}\) and tool diameter \(d\):

$${\varphi }_{i}={\mathrm{cos}}^{-1}\left(1-\frac{2{a}_{e}}{d}\right).$$
(3)

By using the contact angel \({\varphi }_{i}\) the immersion arc \(s\) can be calculated:

$$s=\frac{{\varphi }_{i}}{360}\cdot\uppi \cdot d.$$
(4)

The arc length between two teeth \({l}_{pitch}\) can be obtained with the tool diameter \(d\) and the number of teeth \(z\):

$${l}_{pitch}=\frac{d\cdot\uppi }{z}.$$
(5)

The cutting depth of a tooth, that’s in full engagement \({h}_{tooth}\) can be calculated using the immersion arc \(s\) and tool helix angle \(\lambda \):

$${h}_{tooth}=\frac{s}{\mathrm{tan}(\lambda )}.$$
(6)

The vertical distance between two cutting edges \(\Delta {h}_{tooth}\) is equally calculated from the arc length between two cutting edges \({l}_{pitch}\) and the tool helix angle \(\lambda \):

$$\Delta {h}_{tooth}=\frac{{l}_{pitch}}{\mathrm{tan}\left(\lambda \right)}.$$
(7)

The maximum number of engaged teeth can be determined using the depth of cut \({a}_{p}\) and the vertical distance between two cutting edges \(\Delta {h}_{tooth}\):

$${n}_{tooth}=\lceil\frac{{a}_{p}}{\Delta {h}_{tooth}}\rceil.$$
(8)

In order to determine the qualitative surface error based on the geometric engagement conditions following assumptions are made:

  • The cutting force that a tooth exerts on the fillet during machining in the feed normal direction is proportional to the depth of cut of the tooth \({h}_{tooth}\).

  • The cutting force exerted by a tooth acts as a point load at the center of the depth of cut \({h}_{tooth}\) of the tooth.

  • The bending line of the thin-walled workpiece is equivalent to the bending line of a cantilever beam clamped on one side.

  • The tool compliance is negligible compared to the workpiece compliance.

During climb milling, the outline of the part and thus the dimensional error is created during the disengagement of the cutting edge (see Fig. 2). The surface error at a specific height position can therefore be predicted by looking at the moment at which a cutting edge exits at this position. In the following, therefore, this point in time and the forces and positions of the forces acting on the wall during this moment are determined for each height point of the wall. Based on this information, the resulting surface error can be determined with the use of the bending line.

2.3 Surface Error Over the Wall Height

The surface error \({w}_{ges}(x)\) at every height position \(x\) is calculated individually. The error results from the displacement of the structure by several teeth in contact. For the model, the resulting surface error \({w}_{i}\left(x\right)\) for each tooth \(i\), is calculated separately. Subsequently, the individual errors are summed up for the total error according to the superposition principle:

$${w}_{ges}\left(x\right)=\sum\nolimits_{i=1}^{{2\cdot n}_{tooth}}{w}_{i}(x).$$
(9)

The maximum number of teeth in contact \({n}_{tooth}\) is already determined. Therefore, only \({n}_{tooth}\) cutting edges above and \({n}_{tooth}\) cutting edges below the searched height point \(x\) are considered for the calculation, ensuring that all possible cutting edges in contact are taken into account:

\( \begin{array}{*{20}c} {1 \le i \le n_{{tooth}} } & {{\text{Teeth below the searched height point}}{\text{.}}} \\ {(n_{{tooth}} + 1) \le i \le (2 \cdot n_{{tooth}} )} & {{\text{Teeth above the searched height point}}{\text{.}}} \\ \end{array} \)

The resulting surface error \({w}_{i}\left(x\right)\) at a height point x, which is caused by the tooth i and the force \({F}_{i}\) acting at the position \({a}_{i}\), is known for a cantilever beam of length l:

$${w}_{i}\left(x\right)=\left\{\begin{array}{c}\frac{{F}_{i}}{6EI}(3{a}_{i}{x}^{2}-{x}^{3}), 0\le x<{a}_{i}\\ \frac{{F}_{i}}{6EI}(3{{a}_{i}}^{2}x-{{a}_{i}}^{3}), {a}_{i}\le x\le l\end{array}\right..$$
(10)

The area moment of inertia \(I\) and elastic modulus \(E\) are material constants in the equation that influence the quantitative result. However, the qualitative outcome is independent of these constants, thus they are neglected for the model:

$$EI=1.$$
(11)

According to the assumptions the at a tooth \(i\) acting force \({F}_{i}\) can be substituted by the tooth cutting depth \({h}_{tooth, i}\):

$${F}_{i}\stackrel{\wedge}{=}{h}_{tooth, i}.$$
(12)

The cutting depth of a tooth that is completely in contact has already been determined by \({h}_{tooth}\). However, if the tooth is currently in the entry, exit, or outside the cutting area, the cutting depth must be recalculated. For the cutting edges below the searched height point \(1\le i \le {n}_{tooth}\) the following applies:

$$ h_{{tooth,i}} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {x - i \cdot \Delta h_{{tooth}} + h_{{tooth}} \, < \,0} \hfill \\ {h_{{tooth}} ,} \hfill & {x - i \cdot \Delta h_{{tooth}} + h_{{tooth}} \ge h_{{tooth}} } \hfill \\ {x - i \cdot \Delta h_{{tooth}} + h_{{tooth}} ,} \hfill & {elsewhere} \hfill \\ \end{array} .} \right. $$
(13)

For the cutting edges below the searched height point \(({n}_{tooth}+1)\le i \le ({2\cdot n}_{tooth})\) the following applies:

$$ h_{{tooth,i}} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {x + \left( {i - n_{{tooth}} - 1} \right) \cdot \Delta h_{{tooth}} + h_{{tooth}} \ge a_{p} + h_{{tooth}} } \hfill \\ {h_{{tooth}} ,} \hfill & {x + (i - n_{{tooth}} - 1) \cdot \Delta h_{{tooth}} + h_{{tooth}} \, < \,0} \hfill \\ {a_{p} - (x + (i - n_{{tooth}} - 1) \cdot \Delta h_{{tooth}} ,} \hfill & {elsewhere} \hfill \\ \end{array} .} \right. $$
(14)

According to the assumptions, the position \({a}_{i}\), at which the force of the tooth is applied, occurs at the middle of the engagement height \({h}_{tooth, i}\) of the tooth and can therefore be calculated as follows:

$$ a_{i} = h_{w} + \left\{ {\begin{array}{*{20}l} {x - i \cdot \Delta h_{{tooth}} + \Delta h_{{tooth}} - \frac{{h_{{tooth,i}} }}{2},} \hfill & {1 \le i \le n_{{tooth}} } \hfill \\ {x + \left( {i - n_{{tooth}} - 1} \right) \cdot \Delta h_{{tooth}} + \frac{{h_{{tooth,i}} }}{2},} \hfill & {(n_{{tooth}} + 1) \le i \le (2 \cdot n_{{tooth}} )} \hfill \\ \end{array} .} \right. $$
(15)

2.4 Deformation Damping Due to Tooth Engagement

The preceding calculation describes the expected surface error assuming that the structure reacts freely and immediately to the changing cutting forces. However, because the tool is in contact with the structure during cutting, the contact dampens the movement of the structure. During climb milling, a tooth initially enters the workpiece at a high depth of cut. Due to the helix, the contact area of the tooth moves toward a lower depth of cut during tool rotation. As a time sequence in which the surface error is generated, it can be deduced that first the surface error is generated at a high depth of cut, and with the rotation of the tool the surface error follows at a lower depth of cut.

Due to the damping effect of the tool contact, the generated surface error at a height position is thus dependent on the surface error below this position, since the workpiece can only change its deflection to a limited extent. A downward moving average filter is therefore applied to the calculated surface error to represent this dependence. An interval \(size=2\mathrm{ mm}\) has yielded results close to reality for the investigated parameters:

$${w}_{ges, damped}\left(x\right)=\left[{w}_{ges}\left(x\right)+{w}_{ges}\left(x-\frac{size}{2}\right)+{w}_{ges}\left(x-size\right)\right]/3$$
(16)

3 Experimental Setup

Milling tests were carried out on a FOOKE ENDURA 711 LINEAR to validate the model. Sheets made of Ti-6Al-4V Grade 5 with 2.5 mm wall thickness, 150 mm length and variable heights were clamped and flank milled. In addition to the wall height, the depth of cut, width of cut and tool were varied. An overview of all test parameters of the full-factorial test plan and cemented carbide tools can be found in Table 1. The profile after machining was recorded with a Mahr GD 120 surface profiler at 75 mm length.

Table 1. Cutting parameters and end mills used in full factorial experiments.
Full size table

4 Results and Discussion

4.1 Qualitative Surface-Error-Prediction

Figure 3 shows the measured workpieces after machining and the qualitatively predicted surface error according to Eq. (1) to (16). Figure 3 (a) displays the influence of varying the width of cut. It can be seen that the qualitative, S-shaped progression of the measured dimensional error is well reproduced by the prediction. Figure 3 (b) shows that at different cutting speeds, the resulting surface error is constant. This confirms the prediction by not including the cutting speed in the model. Figure 3 (c) displays the surface error at different tooth feed rates. The feed per tooth also does not appear in the model. However, a higher feed leads to higher cutting forces and thus to a quantitatively larger surface error, as can be seen in the measurement. The qualitative progression remains constant and is well represented by the prediction over the different tooth feeds rates. Figure 3 (d) shows the surface error at different wall heights. It must be noted that the qualitative prediction agrees best with reality at medium wall heights. A deviation at low wall heights can be explained mainly by the fact that the stiffer workpiece increases the influence of tool displacement on the surface error, which is not included in the model. The deviation at greater heights can be explained by the fact that the actual width of cut decreases due to the deflection and thus the effective cutting force and intensity of the S-Curve decreases. This dependency of the effective cutting force to the deflection is not included in the model.

Fig. 3.
figure 3

Measured and predicted surface error with different cutting parameters:

(a) ap 20 mm; ae variable; hw 20 mm; fz 0.07 mm; vc 70 m/min; End Mill 1

(b) ap 20 mm; ae 0.4 mm; hw 20 mm; fz 0.07 mm; vc variable; End Mill 1

(c) ap 20 mm; ae 0.4 mm; hw 20 mm; fz variable; vc 70 m/min; End Mill 1

(d) ap 20 mm; ae 0.4 mm; hw variable; fz 0.07 mm; vc 70 m/min; End Mill 1

(e) ap 10 mm; ae 0,4 mm; hw variable; fz 0.07 mm; vc 70 m/min; End Mill 1

(f) ap 20 mm; ae 0,4 mm; hw variable; fz 0.07 mm; vc 70 m/min; End Mill 2.

Other Parameters according to Table 1 and Chapter 3.

Full size image

Figure 3 (e) displays the dimensional error when using the same tool as in (d), but with a smaller depth of cut. It can be noted, that the S-Shaped surface error is shortened with less turning points and consequently less linear. This can be traced back to less tooths in engagement at the same time. The surface error is therefore strongly dependent on the depth of cut and this dependency is well represented by the model. Figure 3 (f) shows the surface error when using tool 2, which uses more tooth and a higher helix angle compared to (d) that results in more teeth in contact with the workpiece. Same can be found with tool 3. They produces therefore an S-curve with more turning points and less pronounced minima and maxima that leads to a more linear surface error. The model again shows good agreement with the measurement.

4.2 Error-Linearity-Factor Und Error-Compensation-Factor

To validate the model, the characteristic points A, B, C and D of the machining tests were measured and the resulting Error-Linearity-Factor \(\zeta \) and Error-Compensation-Factor \(\xi \) were calculated. The plot of the results together with the predicted values according to Eq. (1) to (16) are shown in Fig. 4.

Figure 4. (a) plots the data points for the Error-Linearity-Factor \(\zeta \). The linear regression shows a coefficient of determination of \({R}^{2}\) = 0.86 and thus a good prediction of the surface error linearity by the provided model. It is therefore suitable for estimating whether the surface error can be compensated by angular adjustment to the tool.

However only a weak correlation between model and reality for the Error-Compensation-Factor \(\xi \), which describes the ratio of minimum to maximum dimensional error, can be seen from Fig. 4. (b). This is confirmed by a low coefficient of determination \({R}^{2}\) = 0.38 obtained from a linear regression. A possible reason for this is the neglect of tool deflection in the model. As a result, the model tends to underestimate the minimum dimensional error for stiffer components (\({h}_{w}\) = 0 mm), since this is largely caused by tool deflection (compare Fig. 3. (f)). On the other hand, large deformations, that leads to a significant reduction in width of cut get overestimated, because the dependency of deformation and less cutting forces, due to the reduced width of cut is not included in the model either. Therefore, the model is only conditionally able to estimate which part of the dimensional error can be compensated by an increased width of cut and should be optimized in further research.

Fig. 4.
figure 4

Experimental validation of the Prediction Model with \(\zeta \) and \(\xi \)

Full size image

5 Summary and Outlook

An analytical model was provided, that can be used to qualitatively predict the surface error after machining of slender, additively manufactured parts based on engagement and tool data without the need of FE-simulations or experiments. The model limits are:

  • too stiff workpieces, where the surface error is mostly a result of the tool bending.

  • too compliant workpieces, where the width of cut gets significantly changed due to the workpiece deformation.

Within its limits the model is able to determine, whether more radial engagement or angular adjustment to the tool is a suitable compensation strategy to reduce the resulting surface error after flank milling. To further open the field of use for the model, a quantitative calculation is needed. Whether such an enlargement in the needed parameters and computing power is in proportion to the gained accuracy is dependent on the application. Further optimization of the model without a quantitative approach could also include different deformation damping intervals based on tooth clearance angle, that is assumed to influence the surface error.