Keywords

1 Introduction

As the deployment of fifth-generation (5G) networks progresses, researchers are increasingly focusing on the advancement of the upcoming sixth-generation (6G) technologies, with significant attention from both academia and industry [1]. In this context, reconfigurable intelligent surface (RIS) has been proposed as a revolutionary technology to support faster and more reliable data transmissions while maintaining at a low cost and energy consumption. An RIS consists of an array of small, cost-effective, and almost passive scattering elements, alongside a programmable controller. This controller is capable of adjusting the phase of the metasurface, thereby altering the reflective properties of an incoming wave [2,3,4]. Hence, researchers have extensively explored the benefits of efficient energy utilization, improved spectrum utilization, cost-effective implementation, and flexible deployment of RIS [5,6,7].

Previous research on double-RIS has predominantly focused on wireless communication systems aided by two distributed RISs [8,9,10,11]. Each RIS independently enhances the communication of its nearby multi-antenna base station (BS) or a cluster of nearby users. Nonetheless, these studies are not applicable to practical scenarios where a single RIS’s reflected signal cannot completely overcome all major obstacles. The initial attempt to jointly design passive beamforming for a wireless communication system assisted by a double-RIS was undertaken by the authors in [12]. However, their approach is not suitable for general scenarios involving multi-antenna BS/users. Another study [13] explored a double RIS-assisted communication system, aiming to optimize the average achievable rate through cooperative passive beamforming. Nevertheless, the algorithm proposed in [13] was computationally intensive due to the utilization of semidefinite relaxation (SDR) and Gaussian randomization techniques. Consequently, only 6 reflecting elements were considered in the simulations.

This study aims to enhance the spectral efficiency in a multi-user context by optimizing the geometric mean (GM) of user rates within a double-RIS framework. We present a low-complexity optimization algorithm for jointly designing beamforming and the quantized programmable reflecting elements (PREs) of RISs to maximize the GM rate. Our algorithm, based on a closed-form approach utilizing the Lagrange multiplier method and linear optimization, provides optimal solutions. Compared to conventional sum rate (SR) based algorithms, our GM rate-based algorithm offers notable advantages. It ensures a fair and equitable distribution of rates among all users without imposing any minimum user-rate constraints. Notably, the proposed GM rate descent algorithm effectively avoids zero-rate users (ZR-UEs), showcasing the efficiency of our approach. We substantiate our claims with simulation results, highlighting the effectiveness of our GM rate-based strategy.

The structure of the remaining sections in this paper is as follows. In Sect. 2, we present the system model for the double RIS-assisted wireless communication system and provide an outline of the optimization problem formulation. In Sect. 3, we present our efficient algorithm designed to tackle the formulated problems within the framework of the double-RIS system. Section 4 presents numerical results to validate the performance of the proposed GM descent algorithm. Lastly, Sect. 5 serves as the conclusion of this paper.

Fig. 1.
figure 1

A MISO wireless communication system assisted by a double-RIS framework.

Full size image

2 Signaling Model

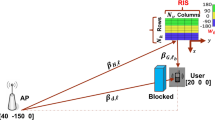
We analyze a downlink communication network assisted by two RISs, as depicted in Fig. 1. This network comprises a BS equipped with N antennas and K individual users, where RIS 1 and RIS 2, each composed of \(M_1\) and \(M_2\) elements respectively, are strategically positioned in proximity to the BS and users. We denote \(\overline{h}_R\in \mathbb {C}^{1\times M_2}\), \(\overline{h}_B\in \mathbb {C}^{M_1\times N}\), and \(\overline{D}\in \mathbb {C}^{M_2\times M_1}\) as the channels for the communication links from RIS 2 to user k, from BS to RIS 1, and from RIS 1 to RIS 2, with \(k\in \mathcal{D}\triangleq \{1,\dots , K\}\), respectively, all of which are modelled by Rician fading. In this research, we assume perfect acquisition of channel state information (CSI) at the BS to demonstrate the enhancement in the performance of the proposed system, as discussed in previous works [14, 15].

The effective channel connecting the BS to user k is represented as

$$\begin{aligned} \bar{\mathcal{H}}_k(\boldsymbol{\varphi }_1,\boldsymbol{\varphi }_2) &\triangleq &\overline{h}_R\pmb {\varPhi }_2 \overline{D}\pmb {\varPhi }_1\overline{h}_B\in \mathbb {C}^{1\times N}, \end{aligned}$$
(1)

for

$$\begin{aligned} \begin{aligned} \pmb {\varPhi }_1\!=\!\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_1})\!=\!\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_{1,1}}, e^{\jmath \bar{\boldsymbol{\psi }}_{1,2}}, \dots , e^{\jmath \bar{\boldsymbol{\psi }}_{1,M_1}}),\bar{\boldsymbol{\psi }}_1\in [0,2\pi ]^{M_1},\\ \pmb {\varPhi }_2\!=\!\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_2})\!=\!\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_{2,1}}, e^{\jmath \bar{\boldsymbol{\psi }}_{2,2}}, \dots , e^{\jmath \bar{\boldsymbol{\psi }}_{2,M_2}}),\bar{\boldsymbol{\psi }}_2\in [0,2\pi ]^{M_2}, \end{aligned} \end{aligned}$$
(2)

where \(\pmb {\varPhi }_1\in \mathbb {C}^{M_1\times M_1}\) and \(\pmb {\varPhi }_2 \in \mathbb {C}^{M_2\times M_2}\) denote the PREs associated with RIS 1 and RIS 2, respectively.

We optimize PREs quantized by b-bit resolutions i.e.

$$\begin{aligned} \bar{\boldsymbol{\psi }}_{1,m_1},\bar{\boldsymbol{\psi }}_{2,m_2}\in \varDelta \triangleq \left\{ \delta \frac{2\pi }{2^b}, \delta =0, 1, \dots , 2^b-1\right\} , \nonumber \\ m_1\in \mathcal{F}_1\triangleq \{1, \dots , M_1\}, m_2\in \mathcal{F}_2\triangleq \{1, \dots , M_2\} . \end{aligned}$$
(3)

Subsequently, the projection of \(\xi \in [0,2\pi )\) onto the set \(\varDelta \), denoted as \(\lfloor \xi \rceil _b\), signifies its approximation with b bits:

$$\begin{aligned} \lfloor \xi \rceil _b=\delta _{\xi }\frac{2\pi }{2^b} \end{aligned}$$
(4)

with

$$\begin{aligned} \delta _{\xi }\triangleq \text{ arg }\min _{\delta = 0, 1,\dots , 2^b-1}\left| \delta \frac{2\pi }{2^b}-\xi \right| , \end{aligned}$$
(5)

which can be easily determined, as we have \(\delta _{\xi } \in {\delta , \delta +1}\) for \(\xi \in [\delta \frac{2\pi }{2^b}, (\delta +1)\frac{2\pi }{2^b}]\). When \(b=\infty \), it is true that

$$\begin{aligned} \xi = \lfloor \xi \rceil _{\infty }. \end{aligned}$$
(6)

Consider \(s_k\in \mathcal{C}(0,1)\) as the information symbol designated for user k, which is directed through beamforming by \(\bar{\textbf{w}}_{k}\in \mathbb {C}^M\). The signal x transmitted from the BS is denoted as

$$\begin{aligned} x=\sum _{k\in \mathcal{D}}\bar{\textbf{w}}_{k}s_k. \end{aligned}$$
(7)

The received signal at user k can be represented as follows:

$$\begin{aligned} \bar{y}_k= & {} \bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\sum _{k\in \mathcal{D}}\bar{\textbf{w}}_{k}s_k+n_k, \end{aligned}$$
(8)

where \(n_k\in \mathcal{C}(0,\sigma )\) represents the background noise at user k.

We define the set \(\bar{\textbf{w}}\) as \(\textbf{w}\triangleq \{\bar{\textbf{w}}_k, k\in \mathcal{D}\}\). The rate at user k can be expressed as

$$\begin{aligned} r_k(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)=\ln \left( 1+\frac{|\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\bar{\textbf{w}}_k|^2}{\sum _{k'\in \mathcal{D}\setminus \{k\}}|\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\bar{\textbf{w}}_{k'}|^2+\sigma } \right) . \end{aligned}$$
(9)

3 GM-Rate Optimization

We express the cooperative optimization of the beamforming vector \(\bar{\textbf{w}}\) for the BS and the PREs \(\bar{\boldsymbol{\psi }}_1\) and \(\bar{\boldsymbol{\psi }}_2\) to optimize the GM of users’ rates in the following manner:

$$\begin{aligned} \max _{\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2}\left( \prod _{k\in \mathcal{D}} r_k(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\right) ^{1/K} \quad \text{ s.t. } \end{aligned}$$
(10a)
$$\begin{aligned} \sum _{k\in \mathcal{D}}||\bar{\textbf{w}}_{k}||^2\le P, \end{aligned}$$
(10b)

while subjecting to a given transmit power P. This issue can be equivalently expressed as the following:

$$\begin{aligned} \min _{\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2}g\left( r_1\left( \bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2\right) , \dots , r_K\left( \bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2\right) \right) \triangleq \frac{1}{\left( \prod _{k\in \mathcal{D}} r_k(\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\right) ^{1/K}}\nonumber \\ \quad \text{ s.t. }\quad (10b). \end{aligned}$$
(11)

The problem becomes non-convex due to the inherent non-convexity of the function \(r_k(\bar{\textbf{w}},\bar{\boldsymbol{\varphi }}_1,\bar{\boldsymbol{\varphi }}_2)\) for \(k\in \mathcal{D}\). Let us denote \((\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\) as a feasible point of (11), which can be derived from the \((\iota -1)\)-th iteration

$$\begin{aligned} {g}' (\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2) \!=\! & {} -\frac{g(r_1(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\varphi }}_2),\dots ,r_K(\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2))}{K\sum _{k\in \mathcal{D}}r_k(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)}, \end{aligned}$$
(12)

The gradient of \(g(\bar{\textbf{w}}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\) is (12), so the linearized function of \(g(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\) at \((r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\dots ,r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}))\) is given by

$$\begin{aligned} 2g\left( r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\dots ,r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\right) -g(r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\dots ,\nonumber \\ r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}))\frac{1}{K}\sum _{k\in \mathcal{D}}\frac{r_k(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)}{r_k(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})}.\qquad \end{aligned}$$
(13)

Considering that \(g\left( r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\dots , r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\right) >0\), we employ the steepest descent method to address the convex function \(g(r_1,\dots , r_K)\), leading to the derivation of the subsequent feasible point \((\bar{w}^{(\iota +1)},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\) [16, 17].

$$\begin{aligned} \max _{\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2}\frac{1}{K}\sum _{k\in \mathcal{D}}\frac{r_k(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)}{r_k(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})}g(r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\dots ,r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}))\nonumber \\ \quad \text{ s.t. }\quad (10b), \end{aligned}$$
(14)

which is equivalent to the subsequent problem:

$$\begin{aligned} \max _{\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2}g^{(\iota )}(\bar{\textbf{w}},\bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\triangleq \sum _{k\in \mathcal{D}} \eta _kr_k(\textbf{w}, \bar{\boldsymbol{\psi }}_1,\bar{\boldsymbol{\psi }}_2)\quad \text{ s.t. }\quad \sum _{k\in \mathcal{D}}||\bar{\textbf{w}}_{k}||^2\!\le \!P. \end{aligned}$$
(15)

for

$$\begin{aligned} \eta _k\!\triangleq \!\frac{g\left( \!r_1(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}),\!\dots , \! r_K(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\right) }{r_k(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})}, k=1,\dots , K. \end{aligned}$$
(16)

3.1 Beamforming Descent Iteration

First, we consider the subproblem of optimizing the beamforming \(\bar{\textbf{w}}\) with given \(\bar{\boldsymbol{\psi }}_1\) and \(\bar{\boldsymbol{\psi }}_2\), and obtain \(\bar{w}^{(\iota +1)}\) such that

$$\begin{aligned} g^{(\iota )}(\bar{w}^{(\iota +1)},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})>g^{(\iota )}(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}). \end{aligned}$$
(17)

Using the inequality [18]

$$ \begin{aligned} \ln \left| I_2+[\textbf{P}]^2(\textbf{Q})^{-1}\right| \ge \ln \left| I_2+[\bar{P}]^2(\bar{Q})^{-1}\right| \nonumber \\ -\langle [\bar{P}]^2(\bar{Q})^{-1}\rangle +2\Re \{\langle \bar{P}^H(\bar{Q})^{-1}\textbf{P}\rangle \}\nonumber \\ -\langle (\bar{Q})^{-1}-(\bar{Q}+[\bar{P}]^2)^{-1},[\textbf{P}]^2+\textbf{Q}\rangle ,\nonumber \\ \forall \ \textbf{P}, \textbf{Q}\succ 0\quad \& \quad \bar{P},\bar{Q}\succ 0, \end{aligned}$$
(18)

we derive a concave quadratic function by approximating \(r^{(\iota )}_k(\bar{\textbf{w}})\) as follows:

$$\begin{aligned} r_k(\bar{\textbf{w}},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})&\ge &r^{(\iota )}_k(\bar{\textbf{w}})\nonumber \\ &\triangleq &\overline{x}^{(\iota )}_k+ 2\Re \{\langle y^{(\iota )}_k,\textbf{w}_k\rangle \}-\overline{z}^{(\iota )}_k\sum _{{k'}\in \mathcal{D}}|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{\textbf{w}}_{k'}|^2, \end{aligned}$$
(19)

with \(\overline{x}^{(\iota )}_k\triangleq r_k(\bar{w}^{(\iota )},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})-|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota )}_k|^2/a^{(\iota )}_k-\sigma a^{(\iota )}_k\), \(y^{(\iota )}_k \triangleq \bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )}\)

\(,\bar{\psi }_2^{(\iota )})\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota )}_k/a^{(\iota )}_k\), \(a^{(\iota )}_k\triangleq \sum _{{k'}\in \mathcal{D}\setminus \{k\}}|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota )}_{k'}|^2+\sigma \), \(0< \overline{z}^{(\iota )}_k\triangleq |\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota )}_k|^2/\left[ a^{(\iota )}_k\left( a^{(\iota )}_k+|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota )}_k|^2\right) \right] \).

Therefore, we determine the value of \(\bar{w}^{(\iota +1)}\) by solving the following problem during the \(\iota \)-th iteration:

$$\begin{aligned} \max _{\bar{\textbf{w}}}\ g^{(\iota )}_1(\bar{\textbf{w}})\quad \text{ s.t. }\quad (10b), \end{aligned}$$
(20)

where

$$\begin{aligned} g^{(\iota )}_1(\bar{\textbf{w}})&\triangleq & \sum _{k\in \mathcal{D}}\eta _k^{(\iota )}r^{(\iota )}_k(\bar{\textbf{w}})\nonumber \\ = & {} \displaystyle \sum _{k\in \mathcal{D}}\eta _k^{(\iota )}\overline{x}^{(\iota )}_k+2\sum _{k\in \mathcal{D}}\Re \{\langle \eta _k^{(\iota )}y^{(\iota )}_k,\bar{\textbf{w}}_k\rangle \}-\sum _{k=1}^{K}(\bar{\textbf{w}}_k)^H\varOmega ^{(\iota )}\bar{\textbf{w}}_k, \end{aligned}$$
(21)

with \(0\preceq \varOmega ^{(\iota )}\triangleq \sum _{{k'}\in \mathcal{D}}\eta _j^{(\iota )}\overline{z}^{(\iota )}_{k'}\bar{\mathcal{H}}^H_{k'}(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{\mathcal{H}}_{k'}(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\).

By employing the Lagrangian multiplier method, the optimal solution for (20) can be expressed in closed form as follows:

$$\begin{aligned} \bar{w}^{(\iota +1)}_k={\left\{ \begin{array}{ll}\begin{array}{ll}(\varOmega ^{(\iota )})^{-1}\eta _k^{(\iota )}y^{(\iota )}_k \quad \text{ if }\displaystyle \sum _{k\in \mathcal{D}} ||(\varOmega ^{(\iota )})^{-1}\eta _k^{(\iota )}y^{(\iota )}_k||^2\le P\\ \left( \varOmega ^{(\iota )}+\rho I_N \right) ^{-1}\eta _k^{(\iota )}y^{(\iota )}_k\qquad \text{ otherwise }, \end{array} \end{array}\right. } \end{aligned}$$
(22)

where \(\rho > 0\) is determined through a bisection process to satisfy the condition: \(\sum _{k\in \mathcal{D}}||\left( \varOmega ^{(\iota )}+\rho I_N \right) ^{-1}\eta _k^{(\iota )}y^{(\iota )}_k||^2= P\).

3.2 PREs of RIS 1 Descent Iteration

Next, our objective is to optimize the subproblem related to the reflecting elements \(\bar{\boldsymbol{\psi }}_1\), while considering the given beamforming \(\textbf{w}\) and \(\bar{\boldsymbol{\psi }}_2\). To achieve this, we aim to find the updated iteration point \(\psi _1^{(\iota +1)}\) that satisfies the following:

$$\begin{aligned} g^{(\iota )}(\bar{w}^{(\iota +1)},\bar{\psi }_1^{(\iota +1)},\bar{\psi }_2^{(\iota )})>g^{(\iota )}(\bar{w}^{(\iota +1)},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )}). \end{aligned}$$
(23)

By applying the inequality (18),

$$\begin{aligned} r_k(\bar{w}^{(\iota +1)},\bar{\boldsymbol{\psi }}_1,\bar{\psi }_2^{(\iota )})&\ge & \overline{r}^{(\iota )}_{1k}(\bar{\boldsymbol{\psi }}_1)\nonumber \\ &\triangleq &2\Re \{(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1)\bar{w}^{(\iota +1)}_k\}/a^{(\iota +1)}_k+\overline{x}^{(\iota )}_{1k}\ \nonumber \\ {} & {} -\overline{z}^{(\iota )}_{1k}\sum _{{k'}\in \mathcal{D}}|\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1)\bar{w}^{(\iota +1)}_{k'}|^2, \end{aligned}$$
(24)

with \(\overline{x}^{(\iota )}_{1k}\triangleq r_k(\bar{w}^{(\iota +1)},\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})-\sigma a^{(\iota +1)}_{1k}-|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota +1)}_k|^2/a^{(\iota +1)}_{1k}\), \(a^{(\iota +1)}_{1k}\)

\(\triangleq \sum _{{k'}\in \mathcal{D}\setminus \{k\}}|\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota +1)}_{k'}|^2+\sigma \), \(0< \overline{z}^{(\iota )}_{1k}\triangleq |\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota +1)}_k|^2/(a^{(\iota +1)}_{1k}\) \((\bar{\mathcal{H}}_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{w}^{(\iota +1)}_k|^2+a^{(\iota +1)}_{1k}))\).

We use \(\varXi _{m_1}\) to represent a matrix of dimensions \(M_1 \times M_1\), where only the element in the \((m_1,m_1)\) position is 1, and all other elements are 0. This matrix is employed to denote as

$$\begin{aligned} \pmb {\varPhi }_1=\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_1})=\sum _{m_1\in \mathcal{F}_1}e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\varXi _{m_1}. \end{aligned}$$
(25)

Using (1), we have (26),

$$\begin{aligned} &(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1)\bar{w}^{(\iota +1)}_k\nonumber \\ =&(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\overline{h}_R\varPhi _2 \overline{D}\pmb {\varPhi }_1\overline{h}_B\bar{w}^{(\iota +1)}_k\nonumber \\ =&(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}}) \overline{D}\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_1})\overline{h}_B\bar{w}^{(\iota +1)}_k\nonumber \\ =&\sum _{m_1\in \mathcal{F}_1}(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}})\overline{D}\mathbf {\varXi }_{m_1}\overline{h}_B\bar{w}^{(\iota +1)}_k e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\nonumber \\ =&\sum _{m_1\in \mathcal{F}_1}\overline{y}^{(\iota )}_{1k}(m_1)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}. \end{aligned}$$
(26)

with \(\overline{y}^{(\iota )}_{1k}(m_1)=(\bar{w}^{(\iota +1)}_k)^H\bar{\mathcal{H}}^H_k(\bar{\psi }_1^{(\iota )},\bar{\psi }_2^{(\iota )})\overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}})\overline{D}\) \(\varXi _{m_1}\overline{h}_B\bar{w}^{(\iota +1)}_k\), \(m_1=1,\dots M_1.\)

Furthermore,

$$\begin{aligned} |\bar{\mathcal{H}}_k(\bar{\boldsymbol{\psi }}_1)\bar{w}^{(\iota +1)}_{k'}|^2 = & {} \left| \overline{h}_R\varPhi _2 \overline{D}\pmb {\varPhi }_1\overline{h}_B\bar{w}^{(\iota +1)}_{k'}\right| ^2\nonumber \\ = & {} \left| \overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}}) \overline{D}\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_1})\overline{h}_B\bar{w}^{(\iota +1)}_{k'}\right| ^2. \end{aligned}$$
(27)

Hence

$$\begin{aligned} \overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}}) \overline{D}\textsf{diag}(e^{\jmath \bar{\boldsymbol{\psi }}_1})\overline{h}_B\bar{w}^{(\iota +1)}_{k'} =\sum _{m_1\in \mathcal{F}_1}b^{(\iota +1)}_{1k,{k'}}(m)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}, \end{aligned}$$
(28)

for \(b^{(\iota +1)}_{1k,{k'}}(m)= \overline{h}_R\textsf{diag}(e^{\jmath \bar{\psi }_2^{(\iota )}}) \overline{D}\varXi _{m_1}\overline{h}_B\bar{w}^{(\iota +1)}_{k'}\), \(m\!=1,\dots , {M}\).

Based on (19), (26), (27) and (28), we obtain

$$\begin{aligned} \overline{r}^{(\iota )}_{1k}(\bar{\boldsymbol{\psi }}_1)= & {} \overline{x}^{(\iota )}_{1k}\!+\!2\Re \{\!\sum _{m_1\in \mathcal{M}_1\!}\!\overline{y}^{(\iota +1)}_{1k}\!(m_1)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\} \!-\!\overline{z}^{(\iota )}_{1k}\!\sum _{\!{k'}\in \mathcal{D}\!}\left| \!\sum _{m_1\in \mathcal{M}_1}\!b^{(\iota +1)}_{1k,{k'}}(m_1)\!e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\!\right| ^2\nonumber \\ = & {} \overline{x}^{(\iota )}_{1k}\!+\!2\Re \{\!\sum _{m_1\in \mathcal{F}_1\!}\!\overline{y}^{(\iota +1)}_{1k}(m_1)\!e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\}\!-\!\overline{z}^{(\iota )}_{1k}\!\sum _{{k'}\in \mathcal{D}\!}\!(e^{\jmath \bar{\boldsymbol{\psi }}_1})^H\varPsi ^{(\iota +1)}_{1k,{k'}}e^{\jmath \bar{\boldsymbol{\psi }}_1}, \end{aligned}$$
(29)

where \(\overline{y}^{(\iota +1)}_{1k}(m_1)\triangleq \overline{y}^{(\iota )}_{1k}(m_1)/a^{(\iota +1)}_k\) and \(\varPsi ^{(\iota +1)}_{1k,{k'}}(m_1,n_1)\triangleq (b^{(\iota +1)}_{1k,{k'}}(m_1))^* b^{(\iota +1)}_{1k,{k'}}\)

\((n_1)\), \(m_1=n_1=1,\dots , {M_1}\).

Note that \(\varPsi ^{(\iota +1)}_{1k,k'}\succeq 0\). Then,

$$\begin{aligned} g^{(\iota )}_2(\bar{\boldsymbol{\psi }}_1)&\triangleq &\sum _{k\in \mathcal{D}}\eta _k^{(\iota )}\overline{r}^{(\iota )}_{1k}(\bar{\boldsymbol{\psi }}_1)\nonumber \\ = & {} \overline{x}^{(\iota +1)}_1+2\Re \{\sum _{m_1\in \mathcal{M}_1}\overline{y}^{(\iota +1)}_1(m_1)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\}-(e^{\jmath \pmb {\theta }_1})^H\varPsi ^{(\iota +1)}_1 e^{\jmath \bar{\boldsymbol{\psi }}_1}, \end{aligned}$$
(30)

for \(\overline{x}^{(\iota +1)}_1\triangleq \sum _{k\in \mathcal{D}}\eta _k^{(\iota )}\overline{x}^{(\iota )}_{1k}\), \(\overline{y}^{(\iota +1)}_1(m_1)\triangleq \sum _{k\in \mathcal{D}}\eta _k^{(\iota )}\overline{y}^{(\iota +1)}_{1k}(m_1)\), \(m_1=1,\dots , {M_1}\), \(0\preceq \varPsi ^{(\iota +1)}_1\triangleq \sum _{k\in \mathcal{D}}\sum _{j\in \mathcal{D}}\eta _k^{(\iota )}\overline{z}^{(\iota )}_{1k}\varPsi ^{(\iota +1)}_{1k,j}\).

Therefore, we obtain the value of \(\bar{\psi }^{(\iota +1)}_1\) by solving the following problem:

$$\begin{aligned} \max _{\bar{\boldsymbol{\varphi }}_1}\ g^{(\iota )}_2(\bar{\boldsymbol{\varphi }}_1), \end{aligned}$$
(31)

\(g^{(\iota )}_2(\bar{\boldsymbol{\varphi }}_1)\) is equivalent to (33). Using the inequality

$$\begin{aligned} \textbf{A}\textbf{B}\textbf{A}^H\!\succeq \!\bar{A}\bar{B}\textbf{A}^H\!+\!\textbf{A}\bar{B}\bar{A}^H\!-\!\bar{A}\bar{B}\textbf{B}^{-1}\bar{B}\bar{A}^H,\forall \ \textbf{B}\succ 0\ ,\ \bar{B}\succ 0, \end{aligned}$$
(32)

we have (34).

$$\begin{aligned} g^{(\iota )}_2(\bar{\boldsymbol{\psi }}_1) = & {} \overline{x}^{(\iota +1)}_1\!+\!2\Re \{\!\sum _{m_1\in \mathcal{M}_1}\!\overline{y}^{(\iota +1)}_1(m_1)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\}-(e^{\jmath \bar{\boldsymbol{\psi }}_1})^H(\varPsi ^{(\iota +1)}_1\!-\!\lambda _{\max }\!(\varPsi ^{(\iota +1)}_1)I_{M_1})\nonumber \\ {} & {} e^{\jmath \boldsymbol{\psi }_1}-\lambda _{\max }\!(\varPsi ^{(\iota +1)}_1)(e^{\jmath \bar{\boldsymbol{\psi }}_1})^HI_{M_1}e^{\jmath \bar{\boldsymbol{\psi }}_1}\nonumber \\ = & {} \overline{x}^{(\iota +1)}_1\!+\!2\Re \{\!\sum _{m_1\in \mathcal{M}_1}\!\overline{y}^{(\iota +1)}_1(m_1)e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\}-(e^{\jmath \boldsymbol{\psi }_1})^H(\varPsi ^{(\iota +1)}_1\!-\!\lambda _{\max }(\varPsi ^{(\iota +1)}_1)I_{M_1})\nonumber \\ {} & {} e^{\jmath \bar{\boldsymbol{\psi }}_1}-\lambda _{\max }(\varPsi ^{(\iota +1)}_1){M_1}. \end{aligned}$$
(33)
$$\begin{aligned} \overline{g}^{(\iota )}_2(\bar{\boldsymbol{\psi }}_1) &\triangleq & \overline{x}^{(\iota +1)}_1\!+\!2\Re \{\!\sum _{m_1\in \mathcal{M}_1\!}\overline{y}^{(\iota +1)}_1(m_1)e^{\jmath \boldsymbol{\psi }_{1,m_1}}\} \!-\![2\Re \{(e^{\jmath \bar{\psi }^{(\iota )}_1})^H(\varPsi ^{(\iota +1)}_1\!-\!\lambda _{\max }(\varPsi ^{(\iota +1)}_1)\nonumber \\ {} & {} I_{M_1})e^{\jmath \bar{\boldsymbol{\psi }}_1}\}\!-\!(e^{\jmath \bar{\psi }^{(\iota )}_1})^H(\varPsi ^{(\iota +1)}_1\!-\!\lambda _{\max } (\varPsi ^{(\iota +1)}_1) I_{M_1})e^{\jmath \bar{\psi }^{(\iota )}_1}]-\lambda _{\max }(\varPhi ^{(\iota +1)}_1){M_1}\nonumber \\ = & {} 2\!\Re \{\!\!\sum _{m_1\in \mathcal{M}_1}(\overline{y}^{(\iota +1)}_1(m_1)\!-\!\!\sum _{n_1\in \mathcal{M}_1}\!\!e^{-\jmath \bar{\psi }^{(\iota )}_{1,n_1}}\!\varPsi ^{(\iota +1)}_1(n_1,m_1) \!+\!\lambda _{\max }(\varPsi ^{(\iota +1)}_1)e^{-\jmath \bar{\psi }^{(\iota )}_{1,m_1}})\nonumber \\ {} & {} e^{\jmath \bar{\boldsymbol{\psi }}_{1,m_1}}\}+\displaystyle \overline{x}^{(\iota +1)}_1-(e^{\jmath \bar{\psi }^{(\iota )}_1})^H\varPsi ^{(\iota +1)}_1 e^{\jmath \bar{\psi }^{(\iota )}_1}-2\lambda _{\max }(\varPsi ^{(\iota +1)}_1){M_1}. \end{aligned}$$
(34)

Hence, we can solve the following problem:

$$\begin{aligned} \max _{\bar{\boldsymbol{\psi }}_1}\ \overline{g}^{(\iota )}_2(\bar{\boldsymbol{\psi }}_1). \end{aligned}$$
(35)

Therefore, the optimal solution of equation (35) in closed-form is given by:

$$\begin{aligned} \bar{\psi }^{(\iota +1)}_{1,m_1} = & {} \!-\!\Big \lfloor \!\angle (\overline{y}^{(\iota +1)}_1(m_1)\!-\!\sum _{n_1\in \mathcal{F}_1}\!\varPsi ^{(\iota +1)}_1(n_1,m_1)\!e^{-\jmath \bar{\psi }^{(\iota )}_{1,n_1}}\!+\!\lambda _{\max }(\varPsi ^{(\iota +1)}_1)\!e^{-\jmath \bar{\psi }^{(\iota )}_{1,m_1}})\!\Big \rceil _b, \nonumber \\ {} & {} \qquad \qquad \qquad m_1=1,\dots ,{M_1}. \end{aligned}$$
(36)

3.3 PREs of RIS 2 Descent Iteration

We turn our attention to the subproblem of optimizing the reflecting elements \(\bar{\boldsymbol{\psi }}_2\) while considering the given beamforming \(\bar{\textbf{w}}\) and \(\bar{\boldsymbol{\varphi }}_1\). We aim to find the next iterative point \(\bar{\psi }_2^{(\iota +1)}\) that satisfies:

$$\begin{aligned} g^{(\iota )}(w^{(\kappa +1)}\!,\!\bar{\psi }_1^{(\iota +1)}\!,\!\bar{\psi }_2^{(\iota +1)})>g^{(\iota )}(w^{(\iota +1)}\!,\!\bar{\psi }_1^{(\iota +1)}\!,\!\bar{\psi }_2^{(\iota )}). \end{aligned}$$
(37)

Continuing with similar steps as in (24) - (33) and using the inequalities (18) and (32), we can derive \(\bar{\psi }^{(\iota +1)}_2\) to solve the following problem:

$$\begin{aligned} \max _{\boldsymbol{\psi }_2}\ \overline{g}^{(\iota )}_3(\bar{\boldsymbol{\varphi }}_2). \end{aligned}$$
(38)

Hence, the similar solution of (38) is given by

$$\begin{aligned} \bar{\psi }^{(\iota +1)}_{2,m_2} = & {} \!-\!\Big \lfloor \!\angle (\overline{y}^{(\iota +1)}_2(m_2)\!-\!\sum _{n_2\in \mathcal{M}_2}\!\varPsi ^{(\iota +1)}_2(n_2,m_2)\!e^{-\jmath \bar{\psi }^{(\iota )}_{2,n_2}}\!+\!\lambda _{\max }(\varPsi ^{(\iota +1)}_2)\!e^{-\jmath \bar{\psi }^{(\iota )}_{2,m_2}})\!\Big \rceil _b, \nonumber \\ {} & {} \qquad \qquad \qquad m_2=1,\dots ,{M_2}. \end{aligned}$$
(39)

3.4 Algorithm

Algorithm 1
figure d

GM descent algorithm

Full size image

4 Numerical Results

This section is dedicated to presenting simulation results that evaluate the effectiveness of the proposed GM descent algorithm in the context of the double RIS system. The simulations are conducted in a three-dimensional coordinate system, where the BS, RIS 1, and RIS 2 are positioned at coordinates (1, 0, 2), (0, 0.5, 1), and (0, 49.5, 1) in meters (m), respectively, as illustrated in Fig. 1. Furthermore, the users are randomly distributed within a circular region centered at (1, 50, 0) with a radius of 10 meters.

The azimuth angles of RIS 1 and RIS 2 relative to the x-axis are configured as \(\pi /4\) and \(3\pi /4\), respectively. For our simulation, we adopt a distance-dependent channel path loss model, which is represented as follows:

$$\begin{aligned} P(d) = G(d/d_0)^{-\alpha }, \end{aligned}$$
(40)

G represents the reference channel power gain at a distance of \(d_0 = 1\) meter, which is configured as \(-30\)dB for the simulation. The variable d corresponds to the path’s link distance, while \(\alpha \) signifies the path loss exponent. In our simulation, we set \(\alpha \) to 2.2 for the link between users/BS and their nearby serving RIS, and 3 for the link between RIS 1 and RIS 2. Furthermore, we incorporate Rician fading in our simulation, where the Rician factor is set at 20dB. We establish the bandwidth as 1 MHz, and the noise power density is set to −174 dBm/Hz.

Unless specified, we assume that the number of antennas \(N=10\), transmit power \(P = 20\)dBm, RIS 1 elements \(M_1 = 50\), RIS 2 elements \(M_2 = 50\), and resolution \(b = 3\). Additionally, it’s important to note that all simulation outcomes presented in this study are based on an average of 30 channel realizations.

  • GM Double-RIS RT: This result evaluates the performance of the GM descent algorithm under the assumption of random phase coefficients \(\boldsymbol{\psi }_1\) and \(\boldsymbol{\psi }_2\) at the RISs in the double-RIS system.

  • 3-bit GM Double-RIS RT: This result assesses the performance of the GM descent algorithm with random phase coefficients \(\boldsymbol{\psi }_1\) and \(\boldsymbol{\psi }_2\) at the RISs in the double-RIS system, considering a resolution of \(b = 3\).

  • SR Double-RIS: This result analyzes the performance of the SR algorithm in the Double-RIS system, with \(\eta _k\) set to 1.

  • 3-bit SR Double-RIS: This result examines the performance of the SR algorithm in the Double-RIS system, with both \(\eta _k\) and the resolution b set to 1 and 3, respectively.

The sum rates of the proposed algorithms are examined in Fig. 2. It is evident that SR Double-RIS and 3-bit SR Double-RIS outperform GM Double-RIS and 3-bit GM Double-RIS, respectively, in terms of cumulative rates. Notably, GM Double-RIS exhibits superior performance compared to 3-bit SR Double-RIS when the number of antennas N is greater than or equal to 8. As expected, the figure shows an upward trend with the increment in the number of antennas N at the BS, attributable to the enhanced spatial diversity.

Fig. 2.
figure 2

Achieved SR versus the number of antennas N.

Full size image

Figure 3 illustrates the rate distribution among the proposed algorithms within the double-RIS system. It is evident from Fig. 3 that the introduced GM descent algorithms possess the capability to prevent the occurrence of zero rate assignments, showcasing their superior performance in this regard.

Fig. 3.
figure 3

Rate distribution.

Full size image

In order to provide empirical evidence for the susceptibility of SR-based algorithms to zero rate allocations, Table 1 presents the average count of ZR-UEs across varying numbers of antennas N. As depicted in Table 1, the count of ZR-UEs demonstrates an upward trend with the reduction of N across all proposed algorithms. Furthermore, the data in Table 1 consistently indicates the presence of ZR-UEs within SR-based algorithms.

Table 1. The average number of ZR-UEs versus the number of antennas N.
Full size table

Figure 4 illustrates the achieved GM rate in relation to the number of antennas N. The figure highlights the superior performance of GM Double-RIS over 3-bit GM Double-RIS. Furthermore, it showcases the comparable performance of GM Double-RIS RT and 3-bit GM Double-RIS RT in the given system. This trend aligns with the anticipated outcome, where all algorithms experience performance enhancement with a rise in the number of antennas N.

Fig. 4.
figure 4

Achieved GM rate versus the number of antennas N.

Full size image

The GM rate is further analyzed across varying power budgets P and the number of RIS elements M, as depicted in Fig. 5 and Fig. 6. As anticipated, the GM rate exhibits an upward trend with the augmentation of the power budget, enabling greater power allocation for information transmission. Furthermore, it is notable that the GM rate experiences an upsurge as M increases. This effect can be attributed to the heightened power capabilities of the reflecting RISs, indicating a positive correlation between the number of RIS elements and the achieved GM rate.

Fig. 5.
figure 5

Achieved GM rate versus the transmit power P.

Full size image
Fig. 6.
figure 6

Achieved GM rate versus the number of RISs elements \(M = 2M_1 = 2M_2 = 100\).

Full size image

Finally, Fig. 7 facilitates a comparison of the performance achieved by the b-bit solution across varying values of b. As anticipated, the b-bit GM Double-RIS algorithm demonstrates improved performance as b increases. Furthermore, Fig. 7 reveals that the b-bit GM Double-RIS RT algorithm does not exhibit significant improvements with increasing values of b. This finding underscores the limitations of the b-bit GM Double-RIS RT approach in benefiting from higher values of b.

Fig. 7.
figure 7

Achieved GM rate vs the value of b.

Full size image

5 Conclusions

We have investigated a communication network assisted by a double-RIS system, comprising a BS equipped with an antenna array to serve multiple users in the downlink direction. To enhance the system’s performance, we have introduced effective alternating descent iteration algorithms. These algorithms aim to optimize the system by maximizing the GM of the users’ rates. This optimization strategy contributes to a balanced distribution of rates among users while ensuring reasonable overall sum rates. Through comprehensive simulations, we have validated the effectiveness and practical applicability of the proposed algorithms.