Abstract
Abstract interpretation offers sound and decidable approximations for undecidable queries related to program behavior. The effectiveness of an abstract domain is entirely reliant on the abstract domain itself, and the worst-case scenario is when the abstract interpreter provides a response of “don’t know", indicating that anything could happen during runtime. Conversely, a desirable outcome is when the abstract interpreter provides information that exceeds a specified level of precision, resulting in a more precise answer. The concept of completeness relates to the level of precision that is forfeited when performing computations within the abstract domain. Our focus is on the domain’s ability to express program behaviour, which we refer to as adequacy. In this paper, we present a domain refinement strategy towards adequacy and a simple sound proof system for adequacy, designed to determine whether an abstract domain is capable of providing satisfactory responses to specified program queries. Notably, this proof system is both language and domain agnostic, and can be readily incorporated to support static program analysis.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The accuracy of an abstract interpretation depends upon many factors [13]. (1) The quality of the abstract domain: In this case the abstract domain has to represent in the most precise way all the intermediate invariants that hold at each program point along a computation trace [5, 6, 10, 11, 19]. (2) The precision of the fixpoint strategy: In this case an appropriate fixpoint strategy can improve the precision of the analysis either by delaying widening/narrowing or dynamic trace partition [2, 8, 12, 27]. (3) The way the code is written: In this case, the non-compositional nature of the precision of abstract interpretation can be influenced by the way the code is assembled [3, 20]. All these factors imply that the design of an optimal (aka, sound and complete) abstract interpretation for static program analysis is a very complex task.
In this paper, we address the first of the above mentioned factors: The quality of the abstract domain. The standard approach is based on the notion of abstract domain refinement [14]. The goal of domain refinement is to remove false alarms by enhancing the expressive power of the abstract domain. In particular, in the last two decades, the notion of completeness, with their global and local refinements [5, 17]—the latter called Abstract Interpretation Repair (AIR), perfectly captures the structure of an abstract domain that will produce no false alarm for a given program. This notion has also been weakened towards what is known as partial completeness [7] where the precision is evaluated in a metric space built over the abstract domain.
Rather than focusing on eliminating false alarms to achieve completeness, or on weaker forms of completeness that tolerate some level of false alarms, our study is concerned with evaluating the expressiveness of an abstract domain with respect to its ability to represent intermediate invariants in the computation. In particular, when dealing with abstract analysis, it is widely recognized that an abstract domain must allow for the possibility of making no statements regarding the behavior of a computation. This characteristic is critical for enabling the analysis to provide decidable answers to otherwise undecidable questions. The primary objective of adequacy is to prevent excessively imprecise statements with respect to a given concrete assertion. When the level of imprecision exceeds a certain threshold, it is deemed unacceptable, namely not fitting, for the purposes of abstract computation. This domain property will be referred to as adequacy of the abstract domain.
Like completeness, an abstract domain may be deemed not adequate because it is overly abstract. In this scenario, we may question whether it is feasible to adjust the abstract domain to ensure adequacy, just as it is possible to eliminate false alarms for achieving completeness by refinement [5, 17]. This proposed approach to achieving adequacy involves a refinement strategy that ensures the refined abstract domain approximates computed invariants more accurately than a specified bound \(\mathtt {\tau }\). However, precisely as it happens for completeness, while the refinement approach is crucial for gaining a deep understanding of adequacy by identifying the elements necessary for enforcing it, it needs the computation of the function/semantics, which may render it an undecidable characterization.
To address this issue, in the context of program analysis, we also introduce a simple proof system, based on structural induction, to verify whether the approximate invariants generated by the abstract interpreter within an abstract domain \(\textsf{A}\) are kept below a the given (abstract) bound \(\mathtt {\tau }\). This is achieved by proving the validity of triples holding on a program \(\texttt{r}\) w.r.t. an input concrete assertions \(\texttt{c}\) and an output one \(\texttt{d}\). If \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\) is the abstract semantics of \(\texttt{r}\) given by an abstract interpreter defined on the abstract domain \(\textsf{A}\), namely \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}:\textsf{A}\rightarrow \textsf{A}\), then if the triple, denoted \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \), is derived in the proof system then we can say that \(\textsf{A}\) is adequate for \(\texttt{r}\), namely the computation of \(\texttt{r}\) semantics on \(\textsf{A}\) is kept under the bound \(\mathtt {\tau }\). The proof system we introduce, which we refer to as the abstract domain adequacy logic, is very simple and can be efficiently checked online using program analysis tools.
Paper Roadmap. Section 2 provides an overview of abstract interpretation and programming language semantics. We chose to treat regular commands as the general programming language to establish a language-agnostic framework. In Sect. 3, we recall abstract domain completeness and introduce the novel concept of abstract domain adequacy. Section 4 outlines the procedure for adjusting an abstract domain towards adequacy by refining it. Finally, in Sect. 5, we present a sound proof system for adequacy, and Sect. 6 concludes the paper with closing remarks and potential future directions.
Related Works. Adequacy is a novel approach here proposed for dealing with abstract domain precision. Completeness in abstract interpretation [17] is the closest notion to adequacy, at least in its origin. As we will demonstrate in Sect. 3, the two concepts are incomparable, meaning that neither one is stronger than the other. Nonetheless, the proof system and domain refinement procedures for both concepts employ similar strategies. Specifically, the proof system inherits the locality of the notion of local completeness introduced in [4] and [6], which also forms the basis for the refinement strategy in abstract interpretation repair (AIR) [5]. As a consequence, the proof systems for global completeness in [19] and local completeness in [6] are logically incomparable with ours. However, the idea of setting a bound on the approximation, which may be weaker than the abstract observation, is a novel aspect of our work.
In the context of local adequacy, as it happens AIR, in general, no optimal (most abstract) refinement exists. Therefore, the process of achieving adequacy can only provide sub-optimal solutions. It should be noted that completeness and adequacy are distinct problems, and as such, the computed refinements produced by the two methods may lead to different domains. An adequate domain may still be incomplete, and thus not a solution in terms of AIR, and vice versa, a solution in terms of AIR may not ensure a bounded abstract computation, and therefore may not be adequate. The technical differences are discussed in Sect. 3.
In [7], the concept of partial completeness is introduced as a means of evaluating the accuracy of an abstract interpretation. This is accomplished by incorporating the abstract domain into a (quasi) metric space, which relaxes the requirement for local completeness to hold up to a metric neighbor of the exact (complete) solution. Along with completeness, partial completeness is also not comparable to adequacy. The latter is not intended to provide any quantitative estimate of the quality of an abstraction but rather an answer of whether the resulting invariant is below (is approximated by) a given bound \(\tau \) in the abstract domain. This guarantees that at least the information in \(\tau \) will be included in the computed approximate invariant.
2 Background
If \(\texttt{S}\), \(\wp (\texttt{S})\) denotes the powerset of \(\texttt{S}\). If \(f: \texttt{S}\rightarrow \texttt{T}\), then we often abuse notation by calling f also its additive lifting \(f: \wp (\texttt{S}) \rightarrow \wp (\texttt{T})\) to sets of values:
 . If \(f:\texttt{S}\longrightarrow \texttt{T}\) and \(g:\texttt{T}\rightarrow \texttt{U}\), we denote by
. If \(f:\texttt{S}\longrightarrow \texttt{T}\) and \(g:\texttt{T}\rightarrow \texttt{U}\), we denote by
 (or simply gf) their composition. If \(f:\texttt{S}\rightarrow \texttt{S}\), and \(n\in \mathbb {N}\) we define \(f^n:\texttt{S}\rightarrow \texttt{S}\) inductively as
(or simply gf) their composition. If \(f:\texttt{S}\rightarrow \texttt{S}\), and \(n\in \mathbb {N}\) we define \(f^n:\texttt{S}\rightarrow \texttt{S}\) inductively as
 (the identity on \(\texttt{S}\)),
(the identity on \(\texttt{S}\)),
 . In a partial ordered structure \(\textsf{C}\), we use \(\le _{{\tiny \textsf{C}}}\) to denote the partial order relation, \(\vee _{\!{\tiny \textsf{C}}}\) for lub, \(\wedge _{{\tiny \textsf{C}}}\) for glb, \(\top _{\!\!{\tiny \textsf{C}}}\) and \(\bot _{{\tiny \textsf{C}}}\) for respectively the greatest and the least elements (we avoid the pedex \(\textsf{C}\) when clear from the context). A function f between ordered structures is monotone if it preserve the order, i.e., \(\texttt{c}\le _{{\tiny \textsf{C}}}\texttt{d}\Rightarrow f(\texttt{c})\le _{{\tiny \textsf{C}}}f(\texttt{d})\). It is additive if it preserves arbitrary lubs (co-additivity is dually defined).
. In a partial ordered structure \(\textsf{C}\), we use \(\le _{{\tiny \textsf{C}}}\) to denote the partial order relation, \(\vee _{\!{\tiny \textsf{C}}}\) for lub, \(\wedge _{{\tiny \textsf{C}}}\) for glb, \(\top _{\!\!{\tiny \textsf{C}}}\) and \(\bot _{{\tiny \textsf{C}}}\) for respectively the greatest and the least elements (we avoid the pedex \(\textsf{C}\) when clear from the context). A function f between ordered structures is monotone if it preserve the order, i.e., \(\texttt{c}\le _{{\tiny \textsf{C}}}\texttt{d}\Rightarrow f(\texttt{c})\le _{{\tiny \textsf{C}}}f(\texttt{d})\). It is additive if it preserves arbitrary lubs (co-additivity is dually defined).
2.1 Abstract Interpretation
Abstract interpretation [10, 11], is a formal framework for approximating programs semantics defined on a concrete domain \(\textsf{C}\), by means of some abstraction \(\textsf{A}\) of \(\textsf{C}\). Given complete lattices \(\textsf{C}\) and \(\textsf{A}\), a pair of functions \(\alpha : \textsf{C}\rightarrow \textsf{A}\) and \(\gamma : \textsf{A}\rightarrow \textsf{C}\) forms a Galois connection (GC for shorts) if for any \(\texttt{c}\in \textsf{C}\) and \(\texttt{a}\in \textsf{A}\) we have \(\alpha (\texttt{c}) \le _{{\tiny \textsf{A}}}\texttt{a}\Leftrightarrow \texttt{c}\le _{{\tiny \textsf{C}}}\gamma (\texttt{a})\). In this case, \(\alpha \) (resp. \(\gamma \)) is the abstraction/left adjoint (resp. concretization/right adjoint), and it is additive (resp. co-additive). Co-additive functions \(g:\textsf{A}\rightarrow \textsf{C}\) admits left adjoint
 . An upper closure operator (uco for shorts) \(\rho : \textsf{C}\rightarrow \textsf{C}\) on a poset \(\textsf{C}\) is monotone, idempotent, and extensive, i.e., \(\forall x \in \textsf{C}.\; \texttt{c}\le _{{\tiny \textsf{C}}}\rho (\texttt{c})\). If in a GC
. An upper closure operator (uco for shorts) \(\rho : \textsf{C}\rightarrow \textsf{C}\) on a poset \(\textsf{C}\) is monotone, idempotent, and extensive, i.e., \(\forall x \in \textsf{C}.\; \texttt{c}\le _{{\tiny \textsf{C}}}\rho (\texttt{c})\). If in a GC
 then it is a Galois insertion (GI) and
then it is a Galois insertion (GI) and
 , simply written \(\gamma \alpha \), is an uco. Let us denote by \({ Abs}(\textsf{C})\) the class of abstract domains (GI or uco) of \(\textsf{C}\). It is well known that \({ Abs}(\textsf{C})\) is isomorphic to the lattice of all ucos on \(\textsf{C}\), therefore when dealing with GI and clear from the context, we abuse notation by denoting as \(\textsf{A}\) both the domain of abstract objects (\(\textsf{A}=\gamma \alpha (\textsf{C})\)) and the closure operator (\(\textsf{A}=\gamma \alpha \)). Given an abstract domain \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)) and a concrete function \(f:\textsf{C}\rightarrow \textsf{C}\), an abstract function \(f^\sharp _{{\tiny \textsf{A}}}:\textsf{A}\rightarrow \textsf{A}\) is a sound approximation of f when
, simply written \(\gamma \alpha \), is an uco. Let us denote by \({ Abs}(\textsf{C})\) the class of abstract domains (GI or uco) of \(\textsf{C}\). It is well known that \({ Abs}(\textsf{C})\) is isomorphic to the lattice of all ucos on \(\textsf{C}\), therefore when dealing with GI and clear from the context, we abuse notation by denoting as \(\textsf{A}\) both the domain of abstract objects (\(\textsf{A}=\gamma \alpha (\textsf{C})\)) and the closure operator (\(\textsf{A}=\gamma \alpha \)). Given an abstract domain \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)) and a concrete function \(f:\textsf{C}\rightarrow \textsf{C}\), an abstract function \(f^\sharp _{{\tiny \textsf{A}}}:\textsf{A}\rightarrow \textsf{A}\) is a sound approximation of f when
 Footnote 1. The best correct approximation (bca) of f in \(\textsf{A}\) is the function
Footnote 1. The best correct approximation (bca) of f in \(\textsf{A}\) is the function
 , any other abstraction is less precise. In this case soundness as domain property is defined as
, any other abstraction is less precise. In this case soundness as domain property is defined as
 .
.
2.2 Regular Commands
Following [4, 28] (see also [29]) we consider the language \(\textrm{Reg}_{{{\,\textrm{Exp}\,}}}\) of regular commands in the top of Fig. 1 (where \(\oplus \) denotes non-deterministic choice and \(*\) is the Kleene closure), parametric on a grammar of expressions \({{\,\textrm{Exp}\,}}\). This language is general enough to represent control-flow graphs of basic expressions and therefore it covers simple deterministic imperative languages.
The Concrete Semantics. Let \(\textrm{Reg}_{{{\,\textrm{Exp}\,}}}\) be a regular language. We assume the basic transfer expressions have a semantics \((\!|\cdot |\!): {{\,\textrm{Exp}\,}}\rightarrow \textsf{C}\rightarrow \textsf{C}\) on a complete lattice \(\textsf{C}\) such that \((\!|\textsf{e}|\!)\) is an additive function. The concrete semantics [28] \({\llbracket \cdot \rrbracket }:\textrm{Reg}_{{{\,\textrm{Exp}\,}}}\rightarrow \textsf{C}\rightarrow \textsf{C}\) of regular commands is inductively defined as follows: Let \(\texttt{c}\in \textsf{C}\)

The Abstract Semantics. Let \(\textsf{A}\in { Abs}(\textsf{C})\), the abstract semantics of regular commands \({\llbracket \cdot \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}:\textrm{Reg}_{{{\,\textrm{Exp}\,}}}\rightarrow \textsf{A}\rightarrow \textsf{A}\) on the abstract domain \(\textsf{A}\) is defined by structural induction as follows:

where we recall that \({\llbracket \textsf{e} \rrbracket }^{{\tiny \textsf{A}}}\) is the bca in \(\textsf{A}\) of \({\llbracket \textsf{e} \rrbracket }\).
By structural induction we can prove that this abstract semantics is monotonic and correct, i.e.,
 (or equivalentely
(or equivalentely
 ).
).
Programs. We consider standard basic transfer functions for expressions used in deterministic while programs: no-op instruction, assignments and Boolean guards, i.e., we consider the regular language \({{\,\mathrm{{\mathfrak {L}}}\,}}\) defined in Fig. 1. Hence, we have to deal with integer variables and with stores. Let us denote \({ Var}(\texttt{r})\) the set of all the variables in \(\texttt{r}\in \textrm{Reg}_{{{\,\textrm{Exp}\,}}}\), and let
 the concrete domain of sets of stores, where the store \({{\,\mathrm{\mathbb {m}}\,}}\in \mathbb {M}\) is a function associating values to a set of variables, i.e., \({{\,\mathrm{\mathbb {m}}\,}}:V\rightarrow \mathbb {Z}\), \(V\subseteq _f{ Var}\) (finite subset).
the concrete domain of sets of stores, where the store \({{\,\mathrm{\mathbb {m}}\,}}\in \mathbb {M}\) is a function associating values to a set of variables, i.e., \({{\,\mathrm{\mathbb {m}}\,}}:V\rightarrow \mathbb {Z}\), \(V\subseteq _f{ Var}\) (finite subset).
In particular, the basic transfer function semantics \((\!|\textsf{e}|\!):\textsf{C}\rightarrow \textsf{C}\) for the expressions of \({{\,\mathrm{{\mathfrak {L}}}\,}}\), is defined as: \(\texttt{M}\in \textsf{C}\) (i.e., \(\texttt{M}\subseteq \mathbb {M}\))

where \((\!|\textsf{a}|\!):\mathbb {M}\rightarrow \mathbb {Z}\) and \((\!|\textsf{b}|\!):\mathbb {M}\rightarrow \{\textbf{tt},\textbf{ff}\}\) are the standard evaluation semantics for arithmetic and boolean expressions, respectively, and where we denote
 the truth semantics of \(\textsf{b}\).
the truth semantics of \(\textsf{b}\).
Note that, the concrete semantics of regular language defined above instantiated to \({{\,\mathrm{{\mathfrak {L}}}\,}}\) corresponds precisely to the denotational semantics defined [9] starting from standard operational semantics of non deterministic choice and iteration [29].
3 From Completeness to Adequacy
Abstract domain completeness is the standard approach used for the characterization of abstract domain precision w.r.t. the computation of the semantics [17]. Let us recall its formal definition.
3.1 Abstract Domain Completeness and its Limits
Let \(\textsf{A}\in { Abs}(\textsf{C})\) be an abstraction of \(\textsf{C}\) and \(f:\textsf{C}\rightarrow \textsf{C}\) a concrete computation on \(\textsf{C}\), e.g., the program semantics, then the abstract function \(f^\sharp _{{\tiny \textsf{A}}}\) is said to be a complete/precise [11, 17] approximation of f on \(\textsf{A}\) if
 . Intuitively, it means that if we abstract \(\texttt{c}\in \textsf{C}\) (the input of f), we apply the f approximation \(f^\sharp _{{\tiny \textsf{A}}}\), we obtain the same abstract element that we would have been obtained by abstracting the result of f applied directly on \(\texttt{c}\) (without an initial abstraction). Note that, if there exists a complete approximation \(f^\sharp _{{\tiny \textsf{A}}}\) of f, then \(f^{{\tiny \textsf{A}}}\) is itself complete. Completeness of \(f^{{\tiny \textsf{A}}}\) intuitively means that \(f^{{\tiny \textsf{A}}}\) is the most precise approximation of f and, in therefore, completeness can be characterized as a domain property. \(\textsf{A}\in { Abs}(\textsf{C})\) is said to be a complete abstraction for f if
. Intuitively, it means that if we abstract \(\texttt{c}\in \textsf{C}\) (the input of f), we apply the f approximation \(f^\sharp _{{\tiny \textsf{A}}}\), we obtain the same abstract element that we would have been obtained by abstracting the result of f applied directly on \(\texttt{c}\) (without an initial abstraction). Note that, if there exists a complete approximation \(f^\sharp _{{\tiny \textsf{A}}}\) of f, then \(f^{{\tiny \textsf{A}}}\) is itself complete. Completeness of \(f^{{\tiny \textsf{A}}}\) intuitively means that \(f^{{\tiny \textsf{A}}}\) is the most precise approximation of f and, in therefore, completeness can be characterized as a domain property. \(\textsf{A}\in { Abs}(\textsf{C})\) is said to be a complete abstraction for f if
 .
.
In a more general setting, let \(f:\textsf{C}_1\rightarrow \textsf{C}_2\) be a function on complete lattices \(\textsf{C}_i\) (potentially different), and let \(\textsf{A}_i\in { Abs}(\textsf{C}_i)\) (for \(i\in \{1,2\}\)) be abstractions, respectively, of input and output domains. In this case, we say that \(\langle \textsf{A}_1,\textsf{A}_2 \rangle \) is a pair of complete abstract domains for f if
 .
.
Note that, this is a global property, since it requires the equality of two functions on all inputs, i.e.,
 . This makes completeness an extremely strong property and indeed, as proved in [4], it holds for all programs in a Turing complete programming language only for trivial abstract domains. This means that the only abstract domains that are complete for all programs are the straightforward ones: the identical abstraction, making abstract and concrete semantics the same, and the top abstraction, making all programs equivalent by abstract semantics. In particular, the authors show that while global completeness can be hard/impossible to achieve, it could well happen that completeness holds locally, i.e. just for some store properties, proving so far what is called local completeness [4], namely
. This makes completeness an extremely strong property and indeed, as proved in [4], it holds for all programs in a Turing complete programming language only for trivial abstract domains. This means that the only abstract domains that are complete for all programs are the straightforward ones: the identical abstraction, making abstract and concrete semantics the same, and the top abstraction, making all programs equivalent by abstract semantics. In particular, the authors show that while global completeness can be hard/impossible to achieve, it could well happen that completeness holds locally, i.e. just for some store properties, proving so far what is called local completeness [4], namely
 for a fixed point \(\texttt{c}\in \textsf{C}\). This weakening makes precision strongly dependent on the point \(\texttt{c}\), implying that among points with the same abstraction we may have both complete and incomplete points.
for a fixed point \(\texttt{c}\in \textsf{C}\). This weakening makes precision strongly dependent on the point \(\texttt{c}\), implying that among points with the same abstraction we may have both complete and incomplete points.
However, both completeness characterizations do not really deal with the loss of precision due to the choice of the abstract observation, since it characterizes only whether there is an extra loss of precision due to the computation on observed/abstracted data (compared with the observation of the concretely computed result). For instance, the \(\top \) abstraction, which cannot distinguish any information, is trivially complete, even if it represents the total loss of precision in the observation of data. Therefore, completeness is unable to account for this type of information loss caused by abstraction, which is why we strive to introduce a new concept of precision for abstract domains that can designate \(\top \) as entirely imprecise. Graphically, the idea is depicted in Fig. 2 for program semantics. Namely, (local) completeness can only avoid the error depicted as blue area, namely the error due to computation on abstract data compared with the abstraction of the concrete computation, while we aim at bounding the total error depicted, namely the error due to the choice of the abstract domain, independently from its potential completeness.
3.2 Abstract Domain Adequacy
In order to move the attention to the whole (abstract) image of all the elements with the same abstraction, loosing the dependency on the chosen point imposed by local completeness while keeping a locality of the property, we propose a novel approach referred to as abstract domain adequacy. We can say that abstract domain adequacy allows us to bound (strictly below a fixed threshold) the total amount of approximation due to data abstraction and abstract computationFootnote 2. The idea is to fix a generic bound \(\mathtt {\tau }\) (at the limit \(\top \)) that we want to confine the loss of precision, namely such that any abstract computation is strictly over-approximated by \(\mathtt {\tau }\).
Definition 1
(Abstract domain adequacy w.r.t. \(\mathtt {\tau }\)).
Let \(\textsf{C}\) be a concrete domain, \(f:\textsf{C}\rightarrow \textsf{C}\), \(\textsf{A}\in { Abs}(\textsf{C})\) one of its abstractions, \(\mathtt {\tau }\in \textsf{A}\) (i.e., \(\textsf{A}=\gamma \alpha \) and \(\gamma \alpha (\mathtt {\tau })=\mathtt {\tau }\in \textsf{C}\)). Then \(\textsf{A}\) is adequate w.r.t. \(\mathtt {\tau }\) for f if
-
(Global)
 and
and -
(Local)

when \(\mathtt {\tau }=\top \) we simply call \(\textsf{A}\) adequate for f, denoted \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(f)\) and \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(f)\).
Example 1
Consider \(\textsf{C}=\wp (\mathbb {Z})\) and \(\textsf{A}={ Sign}\), whose abstract counterpart is depicted on the left of Fig. 3.
Let
 and let
and let
 , then we have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(f)\) since
, then we have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(f)\) since
 , but \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}'}(f)\) with
, but \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}'}(f)\) with
 , since
, since
 , which is the top, hence it does not hold globally, i.e., \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(f)\).
, which is the top, hence it does not hold globally, i.e., \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(f)\).
If we consider \(g=\lambda \texttt{c}.\,\left\{ ~n^2+2 \left| \begin{array}{l}n\in \texttt{c}\end{array} \right. \right\} \), and we consider \(\mathtt {\tau }=\mathbb {Z}_{\ge 0}\), then we have that
 . Hence, \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(g)_\mathtt {\tau }\).
. Hence, \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(g)_\mathtt {\tau }\).
In general, completeness and adequacy are not comparable when \(\exists \texttt{c}.\,\textsf{A}f(\texttt{c})=\top \), since in this case we could have completeness, i.e.,
 but we cannot satisfy adequacy, i.e.,
but we cannot satisfy adequacy, i.e.,
 . Following the other direction, it is clear that adequacy cannot imply completeness. A similar reasoning can be done when we consider adequacy w.r.t. \(\mathtt {\tau }\ne \top \). In general, we can prove the following relation.
. Following the other direction, it is clear that adequacy cannot imply completeness. A similar reasoning can be done when we consider adequacy w.r.t. \(\mathtt {\tau }\ne \top \). In general, we can prove the following relation.
Proposition 1
Let \(\textsf{C}\) be a concrete domain, \(f:\textsf{C}\rightarrow \textsf{C}\) and \(\textsf{A}\in { Abs}(\textsf{C})\). Then for any \(\mathtt {\tau }\in \textsf{A}\), if
 then \(\textsf{A}\) complete imply \(\textsf{A}\) globally adequate w.r.t. \(\mathtt {\tau }\) for f.
then \(\textsf{A}\) complete imply \(\textsf{A}\) globally adequate w.r.t. \(\mathtt {\tau }\) for f.
Example 2
Let us consider \(\textsf{C}\) and f in Example 1, we have shown above that \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}(f)\), but it is trivial to show, and well known, that \({ Sign}\) is complete for f, since
 , since f leaves in the resulting set precisely the same signs that are in the input set, but
, since f leaves in the resulting set precisely the same signs that are in the input set, but
 . Hence, in this case, completeness does not imply adequacy. On the other side, let
. Hence, in this case, completeness does not imply adequacy. On the other side, let
 of the same example, which satisfies adequacy (w.r.t. \(\top =\mathbb {Z}\)) since
of the same example, which satisfies adequacy (w.r.t. \(\top =\mathbb {Z}\)) since
 , but it is not complete, e.g.,
, but it is not complete, e.g.,
 , while
, while
 . Hence, in general, adequacy does not imply completeness.
. Hence, in general, adequacy does not imply completeness.
3.3 Adequacy for \({{\,\mathrm{{\mathfrak {L}}}\,}}\) Programs
Let us consider now abstract domain adequacy for \({{\,\mathrm{{\mathfrak {L}}}\,}}\) programs, namely where \(f={\llbracket \texttt{r} \rrbracket }\), for some \(\texttt{r}\in {{\,\mathrm{{\mathfrak {L}}}\,}}\). In this case, the concrete domain is \(\textsf{C}=\wp (\mathbb {M})\) and \(\textsf{A}\in { Abs}(\wp (\mathbb {M}))\) (namely \(\le _{{\tiny \textsf{C}}}\) is \(\subseteq \), while \(\le _{{\tiny \textsf{A}}}\) still depends on the abstract domain, and in particular on the abstraction \(\alpha \)) and we say that \(\textsf{A}\) is adequate for \(\texttt{r}\). For the sake of readability, we will write \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})\) instead of \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}({\llbracket \texttt{r} \rrbracket })\) (analogous for global adequacy). In this context, we look as properties of elements in \({{\,\mathrm{{\mathfrak {L}}}\,}}\) related with adequacy.
In [4] the authors introduce a notion of expressability which has a strong relation with completeness. Formally, \(\textsf{b}\) is expressible in \(\textsf{A}\) if its truth semantics is an element of \(\textsf{A}\), i.e., \((\!|\textsf{b}|\!)\in \textsf{A}\). In particular, the authors show that if the semantics of \(\textsf{b}?\) is local complete then \(\textsf{b}\) and \(\lnot \textsf{b}\) are expressible, while the other implication does not always holds (Lemma III.2 [4]).
As far as adequacy is concerned, the situation is slightly different: while adequacy seems too weak to imply \(\textsf{b}\) to be expressible, it is instead implied by the expressability of \(\textsf{b}\).
Definition 2
(\(\textsf{b}\) quasi-expressible w.r.t. \(\mathtt {\tau }\)). Let \(\textsf{C}=\wp (\mathbb {M})\) be the concrete domain, \(\textsf{A}\in { Abs}(\textsf{C})\), \(\mathtt {\tau }\in \textsf{A}\). A boolean expression \(\textsf{b}\), such that \((\!|\textsf{b}|\!)\le \tau \), is quasi-expressible w.r.t. \(\mathtt {\tau }\) in \(\textsf{A}\) if there exists \(\textsf{b}'\) expressible in \(\textsf{A}\), i.e., \((\!|\textsf{b}'|\!)\in \textsf{A}\), such that \((\!|\textsf{b}|\!)\subseteq (\!|\textsf{b}'|\!)\), \(\textsf{A}((\!|\textsf{b}|\!))=\textsf{A}((\!|\textsf{b}'|\!))=(\!|\textsf{b}'|\!)\subsetneq \mathtt {\tau }\).
In other words, a quasi-expressible, w.r.t. \(\mathtt {\tau }\), boolean expression \(\textsf{b}\) has an abstract semantics approximated in \(\textsf{A}\) strictly under \(\mathtt {\tau }\). It is trivial to observe that, if \(\textsf{b}\) is not quasi-expressible, w.r.t. \(\mathtt {\tau }\) then \(\textsf{A}((\!|\textsf{b}|\!))=\mathtt {\tau }\). For instance, consider again the sign domains in Fig. 3. Then the boolean expressions \(x\le 0\) and \(0<x\) are expressible (and therefore quasi-expressible) in \({ Sign}\), since \(x\le 0\) is expressed by \(\left\{ ~n \left| \begin{array}{l}n\le 0\end{array} \right. \right\} \) and \(0<x\) by \(\left\{ ~n \left| \begin{array}{l}n<0\end{array} \right. \right\} \). Note that \(0<x\) is only quasi-expressible, instead, in \({ Sign}_1\). If we consider the interval domain \({ Int}\) and \(\mathtt {\tau }=[0,+\infty ]\), then \(10<x\) is still expressible also w.r.t. \(\mathtt {\tau }\) since its semantics, i.e., \([11,+\infty ]\) is strictly contained in \(\mathtt {\tau }\), \(x>0\wedge x\ { mod}\ 2=0\), i.e., the set of even numbers greater or equal to 2, is only quasi-expressible w.r.t. \(\tau \), since its semantics is contained in the semantics of \(x\ge 2\), which is \([2,+\infty ]\subsetneq \mathtt {\tau }\), while \(x<100\) is not expressible w.r.t. \(\mathtt {\tau }\) since its semantics is \([-\infty ,99]\), and there is no semantics strictly contained in \(\mathtt {\tau }\) which contains \([-\infty ,99]\).
Theorem 1
Given \(\textsf{b}\in {{\,\textrm{BExp}\,}}\), in the hypotheses of Definition 2
-
1.
If \(\textsf{b}\) is quasi-expressible w.r.t \(\mathtt {\tau }\in \textsf{A}\) then \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{}(\textsf{b}?)_\mathtt {\tau }\);
-
2.
If \(\textsf{b}\) is not quasi-expressible w.r.t. \(\mathtt {\tau }\) then \(\forall \texttt{c}\in \textsf{C}.\,\textsf{A}(\texttt{c})\supseteq \mathtt {\tau }\) we have \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\textsf{b}?)_\mathtt {\tau }\).
Proof
-
1.
Let \(\textsf{b}\) be quasi-expressible w.r.t. \(\mathtt {\tau }\), hence there exists \(\textsf{b}'\in {{\,\textrm{BExp}\,}}\) such that \(\textsf{A}((\!|\textsf{b}|\!))=\textsf{A}((\!|\textsf{b}'|\!))=(\!|\textsf{b}'|\!)\subsetneq \mathtt {\tau }\) and let \(\texttt{c}\in \textsf{C}\). Then

-
2.
Suppose \(\textsf{b}\) is not quasi-expressible w.r.t. \(\mathtt {\tau }\), i.e., \(\textsf{A}((\!|\textsf{b}|\!))=\mathtt {\tau }\), and \((\!|\textsf{b}|\!)\subseteq \mathtt {\tau }\), and suppose \(\textsf{A}(\texttt{c})\supseteq \mathtt {\tau }\), then \((\!|\textsf{b}|\!)\subseteq \mathtt {\tau }\subseteq \textsf{A}(\texttt{c})\) and therefore we trivially have \(\textsf{A}{\llbracket \textsf{b}? \rrbracket } \textsf{A}(\texttt{c})=\textsf{A}(\textsf{A}(\texttt{c})\cap (\!|\textsf{b}|\!))=\textsf{A}((\!|\textsf{b}|\!))=\mathtt {\tau }\).
In other words, when \(\textsf{b}\) is quasi-expressible we have the adequacy of the abstract domain w.r.t. its semantics, when we have adequacy of the abstract domain w.r.t. its semantics, we cannot say anything about the possibility to express \(\textsf{b}\), in particular if \(\textsf{A}(\texttt{c})\subsetneq \mathtt {\tau }\) we always have adequacy w.r.t. \(\mathtt {\tau }\).
Corollary 1
Given \(\textsf{b}\in {{\,\textrm{BExp}\,}}\) and \(\textsf{A}\in { Abs}(\textsf{C})\)
-
1.
If \(\textsf{b}\) is quasi-expressible then \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{}(\textsf{b})\);
-
2.
If \(\textsf{b}\) is not quasi-expressible (w.r.t. \(\top \)), then \(\forall \texttt{c}\in \textsf{C}.\,\textsf{A}(\texttt{c})=\top \) we have \(\lnot \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\textsf{b}?)\).
4 Adjusting Abstract Domains
In this section, we wonder whether it is possible to adjust abstract domains in order to make them locally adequate. First, we realize that, differently from completeness, even when we deal with different input and output abstract domains, i.e.,
 , we have only one possible direction for adjusting the domains, we can only refine them.
, we have only one possible direction for adjusting the domains, we can only refine them.
A second observation is that it is not always possible to adjust an abstract domain towards adequacy.
Finally, even when possible there may not exist a shell [17], namely a most abstract refinement guaranteeing adequacy, but anyway we can adjust the domain towards an optimal refinement guaranteeing adequacy.
For the sake of simplicity, in the following we consider the same domain of input and output, but similar results hold in the most general case.
Proposition 2
Let \(\textsf{C}\) be concrete the domain, \(f:\textsf{C}\rightarrow \textsf{C}\), and \(\textsf{A}\in { Abs}(\textsf{C})\). Let \(\texttt{c}\in \textsf{C}\) and \(\mathtt {\tau }\in \textsf{A}\), if
 then the abstract domain \(\textsf{A}\) cannot be adequate.
then the abstract domain \(\textsf{A}\) cannot be adequate.
For a generic \(\mathtt {\tau }\),
 means that \(\mathtt {\tau }\le _{{\tiny \textsf{C}}}f(\texttt{c})\) or not comparable, when \(\mathtt {\tau }=\top \), it means \(f(\texttt{c})=\top \). The result is trivial, since if \(\textsf{A}\) is such that
means that \(\mathtt {\tau }\le _{{\tiny \textsf{C}}}f(\texttt{c})\) or not comparable, when \(\mathtt {\tau }=\top \), it means \(f(\texttt{c})=\top \). The result is trivial, since if \(\textsf{A}\) is such that
 then also \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by extensivity, contradicting the hypothesis. Hence surely adequacy is violated for any possible abstraction \(\textsf{A}\). For instance, if we consider f of Example 1, \(\texttt{c}=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n\ge 0\end{array} \right. \right\} \) and \(\mathtt {\tau }=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n>0\end{array} \right. \right\} \), then \(f(\texttt{c})=\left\{ ~2n\in \mathbb {Z} \left| \begin{array}{l}n\ge 0\end{array} \right. \right\} \not \le _{{\tiny \textsf{C}}}\mathtt {\tau }\) meaning that there not exist abstract domains \(\textsf{A}\) adequate for f on \(\texttt{c}\)..
then also \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by extensivity, contradicting the hypothesis. Hence surely adequacy is violated for any possible abstraction \(\textsf{A}\). For instance, if we consider f of Example 1, \(\texttt{c}=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n\ge 0\end{array} \right. \right\} \) and \(\mathtt {\tau }=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n>0\end{array} \right. \right\} \), then \(f(\texttt{c})=\left\{ ~2n\in \mathbb {Z} \left| \begin{array}{l}n\ge 0\end{array} \right. \right\} \not \le _{{\tiny \textsf{C}}}\mathtt {\tau }\) meaning that there not exist abstract domains \(\textsf{A}\) adequate for f on \(\texttt{c}\)..
Suppose now \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), then we may adjust the abstract domain. The following step consists in fixing a first necessary (not sufficient) condition, namely
 . Indeed it is necessary since, if
. Indeed it is necessary since, if
 then, by extensivity,
then, by extensivity,
 . Let us define the following set of elements and domain refinementFootnote 3
. Let us define the following set of elements and domain refinementFootnote 3

where the domain operation \(\boxplus \) [5] is defined as follows. Let \(\textsf{A}\in { Abs}(\textsf{C})\) and \(R\subseteq \textsf{C}\)Footnote 4

Proposition 3
Let \(\textsf{C}\) be the concrete domain, \(f:\textsf{C}\rightarrow \textsf{C}\) monotone, and \(\textsf{A}\in { Abs}(\textsf{C})\). Suppose \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) and
 Then
Then
 is such that
is such that
 .
.
Proof
Let us denote
 for the sake of readability. Suppose, in particular \(\textsf{A}_i=\textsf{A}\boxplus \{\texttt{d}\}\), with \(\texttt{d}\in \textsf{R}\). Note that \(\textsf{A}_i\in { Abs}(\textsf{C})\) by construction, and \(\textsf{A}_i\sqsubseteq \textsf{A}\). Now, let us observe that \(\texttt{c}\in \textsf{R}\) since \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by hypothesis, hence \(\texttt{c}\le _{{\tiny \textsf{C}}}\texttt{d}\). Then, by monotonicity of \(\textsf{A}_i\), this means that \(\textsf{A}_i(\texttt{c})\le _{{\tiny \textsf{C}}}\textsf{A}_i(\texttt{d})=\texttt{d}\), where the last equality holds by construction. But then, by definition of \(\textsf{R}\), we have \(f(\texttt{d})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), and therefore
for the sake of readability. Suppose, in particular \(\textsf{A}_i=\textsf{A}\boxplus \{\texttt{d}\}\), with \(\texttt{d}\in \textsf{R}\). Note that \(\textsf{A}_i\in { Abs}(\textsf{C})\) by construction, and \(\textsf{A}_i\sqsubseteq \textsf{A}\). Now, let us observe that \(\texttt{c}\in \textsf{R}\) since \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by hypothesis, hence \(\texttt{c}\le _{{\tiny \textsf{C}}}\texttt{d}\). Then, by monotonicity of \(\textsf{A}_i\), this means that \(\textsf{A}_i(\texttt{c})\le _{{\tiny \textsf{C}}}\textsf{A}_i(\texttt{d})=\texttt{d}\), where the last equality holds by construction. But then, by definition of \(\textsf{R}\), we have \(f(\texttt{d})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), and therefore
 .
.
The following step consists in fixing another necessary (not sufficient) condition, namely
 , which still may not hold. First of all, let us observe that if \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), being \(\mathtt {\tau }\in \textsf{A}\), by monotonicity we have
, which still may not hold. First of all, let us observe that if \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), being \(\mathtt {\tau }\in \textsf{A}\), by monotonicity we have
 , hence
, hence
 means
means
 . In this case we can refine the output abstract domain to force
. In this case we can refine the output abstract domain to force
 .
.
Let us define the following refinement

Proposition 4
Let \(\textsf{C}\) be the concrete domain, \(f:\textsf{C}\rightarrow \textsf{C}\) monotone, and \(\textsf{A}\in { Abs}(\textsf{C})\). Suppose \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) and
 . Then
. Then
 is such that
is such that
 .
.
Proof
Let us denote the set
 for the sake of readability. Suppose, in particular \(\textsf{A}_o=\textsf{A}\boxplus \{\texttt{d}'\}\), with \(\texttt{d}'\in \textsf{R}\). Note that \(\textsf{A}_o\in { Abs}(\textsf{C})\) by construction, and \(\textsf{A}_o\sqsubseteq \textsf{A}\), namely it is more concrete than \(\textsf{A}\), which means that
for the sake of readability. Suppose, in particular \(\textsf{A}_o=\textsf{A}\boxplus \{\texttt{d}'\}\), with \(\texttt{d}'\in \textsf{R}\). Note that \(\textsf{A}_o\in { Abs}(\textsf{C})\) by construction, and \(\textsf{A}_o\sqsubseteq \textsf{A}\), namely it is more concrete than \(\textsf{A}\), which means that
 . Now, let us observe that \(f(\texttt{c})\in \textsf{R}\) since \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by hypothesis, hence \(f(\texttt{c})\le _{{\tiny \textsf{C}}}\texttt{d}'\). Then, by monotonicity of \(\textsf{A}_o\), this means that
. Now, let us observe that \(f(\texttt{c})\in \textsf{R}\) since \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\) by hypothesis, hence \(f(\texttt{c})\le _{{\tiny \textsf{C}}}\texttt{d}'\). Then, by monotonicity of \(\textsf{A}_o\), this means that
 , where the last equation holds by construction. But then, by definition of \(\textsf{R}\), we have \(\texttt{d}'\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), and therefore
, where the last equation holds by construction. But then, by definition of \(\textsf{R}\), we have \(\texttt{d}'\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), and therefore
 .
.
Now we can make the final step, combining the two transformations.
Theorem 2
Let \(\textsf{C}\) be the concrete domain, \(f:\textsf{C}\rightarrow \textsf{C}\) monotone, and \(\textsf{A}\in { Abs}(\textsf{C})\). Suppose \(f(\texttt{c})\lneq _{{\tiny \textsf{C}}}\mathtt {\tau }\), then let
 and
and
 , then
, then
 .
.
Proof
By the hypotheses and by Proposition 3 we have that
 . Let us denote
. Let us denote
 , then \(f(\texttt{c}')\lneq \mathtt {\tau }\), hence we can build
, then \(f(\texttt{c}')\lneq \mathtt {\tau }\), hence we can build
 . At this point, by definition and indempotence of \(\textsf{A}_i\) we have that
. At this point, by definition and indempotence of \(\textsf{A}_i\) we have that
Hence \(\textsf{A}_o=\textsf{Ro}^{\mathtt {\tau }}_{{\tiny \textsf{A}_i(\texttt{c})}}(\textsf{A}_i)=\textsf{R}^{\mathtt {\tau }}_{{\tiny \textsf{A}(\texttt{c})}}(\textsf{A})\) and \(\textsf{A}_o\sqsubseteq \textsf{A}_i\). Then by Proposition 4 we have that
 , namely
, namely
 . But then, by \(\textsf{A}_o\sqsubseteq \textsf{A}_i\) and by monotonicity of the functions involved, we have
. But then, by \(\textsf{A}_o\sqsubseteq \textsf{A}_i\) and by monotonicity of the functions involved, we have
 .
.
Let us consider a very simple example just to show the process.
Example 3
Consider the sign abstraction \(\textsf{A}={ Sign}\) on the concrete domain \(\textsf{C}=\wp (\mathbb {Z})\) and
 . Then, if
. Then, if
 we have \(g(\texttt{c})=\top \), meaning that for the \(\top \) element the sign domain cannot be make adequate.
we have \(g(\texttt{c})=\top \), meaning that for the \(\top \) element the sign domain cannot be make adequate.
Let us consider now the f function in Example 1, on the same domains and suppose
 . Let \(\texttt{c}=\{0,2,4\}\), then
. Let \(\texttt{c}=\{0,2,4\}\), then
 , but
, but
 hence we can try to make the abstract domain adequate for \(\texttt{c}\). Let us observe that for any \(n>0\)
hence we can try to make the abstract domain adequate for \(\texttt{c}\). Let us observe that for any \(n>0\)

since
 , but
, but
 since 0 is still in the result. Let us define
since 0 is still in the result. Let us define
 . Now
. Now
 , but unfortunately
, but unfortunately
 , hence we have to further refine. Then, we have that
, hence we have to further refine. Then, we have that

Let
 , and in this case
, and in this case
 and
and
 Footnote 5
Footnote 5
 . In this example, we can also observe that, in general, the refinements do not induce local completeness [5] but only adequacy.
. In this example, we can also observe that, in general, the refinements do not induce local completeness [5] but only adequacy.
5 Abstract Domain Adequacy Logic
In this section we define a proof system for program analysis of regular commands, parameterized by an abstraction \(\textsf{A}=\gamma \alpha (\textsf{C})\) on the concrete domain of sets of stores \(\textsf{C}=\wp (\mathbb {M})\). The provable triples of our logic are judgements of the form \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \), with \(\texttt{c},\texttt{d}\in \textsf{C}\), \(\mathtt {\tau }\in \textsf{A}\) and \(\texttt{r}\in {{\,\mathrm{{\mathfrak {L}}}\,}}\). \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) guarantees that:
-
1.
\(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\);
-
2.
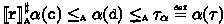 .
.
The rules are provided in Fig. 4. It is worth noting that, the rule relax is added, even if less common, since the rules work with the concrete elements \(\texttt{c}\), and the rule seq could be not directly applicable also in cases where the first statement has an output assertion greater than the input assertion of the following statement. In this case the rule relax\(_2\) may not be used or may increase imprecision getting closer to \(\tau \).
For instance, consider \(\texttt{r}=\texttt{r}_1;\texttt{r}_2\), and consider as output property of \(\texttt{r}_1\) the property \(\texttt{c}=\{0,10,20,30\}\), while the input property for \(\texttt{r}_2\) is \(\texttt{c}'=\{0,10,30\}\), then we would have to reduce \(\texttt{c}\) or enlarge \(\texttt{c}'\) in order to apply rule seq. It should be clear that the first direction is surely preferable for not losing precision and only the rule relax allows to follow such direction.
Lemma 1
Let \(\textsf{C}=\wp (\mathbb {M})\), \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)), \(\mathtt {\tau }\in \textsf{A}\) and
 . Then \(\forall \texttt{c}\in \textsf{C}\) we have that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) iff \(\alpha ({\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c}))\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
. Then \(\forall \texttt{c}\in \textsf{C}\) we have that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) iff \(\alpha ({\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c}))\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
Proof
Suppose \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\), namely such that \(\textsf{A}{\llbracket \texttt{r} \rrbracket } \textsf{A}(\texttt{c})\subsetneq \mathtt {\tau }\), written in terms of the GI it is \(\gamma \alpha {\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c})\subsetneq \mathtt {\tau }\), then by monotonicity of \(\alpha \) and by properties of GI, we have that
Suppose, towards contradiction, that \(\alpha {\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c})=\mathtt {\tau _\alpha }\), then since \(\gamma (\mathtt {\tau _\alpha })=\gamma \alpha (\mathtt {\tau })=\mathtt {\tau }\) being \(\mathtt {\tau }\in \textsf{A}\), we would have also
contradicting the hypothesis, hence \(\alpha {\llbracket \texttt{r} \rrbracket } \gamma \alpha (\texttt{c})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
Suppose now \(\alpha {\llbracket \texttt{r} \rrbracket } \gamma \alpha (\texttt{c})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), then by monotonicity of \(\gamma \), we have
Suppose, towards contradiction, that \(\gamma \alpha {\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c})=\gamma (\mathtt {\tau _\alpha })\) then being \(\gamma \) one-to-one, this would imply \(\alpha {\llbracket \texttt{r} \rrbracket } \gamma \alpha (\texttt{c})=\mathtt {\tau _\alpha }\) contradicting the hypothesis. Hence \(\textsf{A}{\llbracket \texttt{r} \rrbracket }\textsf{A}(\texttt{c})\subsetneq \mathtt {\tau }\).
Theorem 3
Let \(\texttt{c},\texttt{d}\in \textsf{C}=\wp (\mathbb {M})\), \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)), \(\mathtt {\tau }\in \textsf{A}\) and
 . If \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) then (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
. If \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) then (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
Proof
We prove the soundness of the rule system in Fig. 4 by structural induction on the derivation tree of \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \), by distinguishing the cases depending on the last rule applied.
(transfer): In this case (1) holds by hypothesis, being the premix of the rule. Then, by Lemma 1 we have \(\alpha ({\llbracket \textsf{e} \rrbracket }\gamma \alpha (\texttt{c}))\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), and by definition of \({\llbracket \textsf{e} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\) we have
(relax): First of all, let us observe that the hypotheses, by monotonicity and idempotence of \(\gamma \alpha \), imply \(\gamma \alpha (\texttt{c})=\gamma \alpha (\texttt{c}')\), and therefore, being \(\gamma \) one-to-one, this means that \(\alpha (\texttt{c})=\alpha (\texttt{c}')\). Analogously, \(\alpha (\texttt{d})=\alpha (\texttt{d}')\). This means that \(\alpha ({\llbracket \texttt{r} \rrbracket } \gamma \alpha (\texttt{c}))=(\alpha {\llbracket \texttt{r} \rrbracket } \gamma )\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}{\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\) by definition of bca, but then \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})={\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c}')\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) since by hypothesis \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}'\rangle \,\texttt{r}\,\langle \texttt{d}'\rangle \), and therefore by inductive hypothesis \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c}')\le _{{\tiny \textsf{A}}}\alpha (\texttt{d}')\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). But then, by definition of bca and by transitivity of \(\le _{{\tiny \textsf{A}}}\) we have \(\alpha ({\llbracket \texttt{r} \rrbracket }\gamma \alpha (\texttt{c}))\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). Hence, by Lemma 1 we have (1). As far as (2) is concerned, by we have proved above we have
(relax\(_2\)): Note that, by hypothesis \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}'\rangle \,\texttt{r}\,\langle \texttt{d}'\rangle \), hence by inductive hypothesis, as before, we have \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c}')\le _{{\tiny \textsf{A}}}\alpha (\texttt{d}')\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), and therefore
Then by Lemma 1 this implies \(\textsf{A}{\llbracket \texttt{r} \rrbracket }\textsf{A}(\texttt{c})\subsetneq \mathtt {\tau }\) (condition (1)), and moreover, again by the rule hypotheses and by inductive hypothesis, we have
proving condition (2).
(seq): Let us prove (1). By inductive hypotheses, we have that \({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d}')\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) and \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{d}')\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), then by definition of bca and of abstract semantics, and by the monotonicity of the abstract semantics we have that
Hence, by Lemma 1, we have \(\textsf{A}{\llbracket \texttt{r} \rrbracket }\textsf{A}(\texttt{c})\subsetneq \mathtt {\tau }\). As far as (2) is concerned, we have already proved that \({\llbracket \texttt{r}_1;\texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}{\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{d}')\), and \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{d}')\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) by hypothesis (2) on \(\texttt{r}_2\), and therefore by transitivity we have the thesis.
(iterate): Let us prove that if we have \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) with \(\alpha (\texttt{d})\le _{{\tiny \textsf{A}}}\alpha (\texttt{c})\), then we have \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}^*\,\langle \texttt{c}\rangle \). We first prove by induction on \(n\ge 1\) that \(({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\). The base (\(n=1\)) is the hypothesis of the rule, suppose it holds for \(({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\), let us prove for \(n+1\), recalling that by structural inductive hypothesis we have that \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\subsetneq \mathtt {\tau _\alpha }\), and by the rule hypothesis we have \(\alpha (\texttt{d})\le _{{\tiny \textsf{A}}}\alpha (\texttt{c})\)

where the last relations hold by inductive hypothesis on n. Hence, for all \(n\ge 1\) we have \(({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). At this point we have condition (2)
by additivity of \(\alpha \) and by the rule hypothesis \(\alpha (\texttt{c})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). Finally, condition (1) comes by Lemma 1.
(join): Let us prove (2). By inductive hypotheses we have that \({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d}_1)\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) and that \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d}_2)\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). Hence, by additivity of \(\alpha \) we have
By Lemma 1 what we have proved implies also (1), proving the thesis.
Corollary 2
Let \(\textsf{C}=\wp (\mathbb {M})\), \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)). If \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) then \((1)\ \ \widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})\ {and}\ (2)\ \ {\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\top _{\!\!{\tiny \textsf{A}}}\).
Let us investigate about completeness of this rule system.
Theorem 4
Let \(\texttt{c},\texttt{d}\in \textsf{C}=\wp (\mathbb {M})\), \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)), \(\texttt{r}\in {{\,\mathrm{{\mathfrak {L}}}\,}}\), \(\mathtt {\tau }\in \textsf{A}\) and
 . (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) do not imply \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \).
. (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) do not imply \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \).
Proof (Sketch)
We provide an example that cannot be deduced by using the rule system. Consider
 , let us denote by
, let us denote by
 and by
and by
 . Consider the sign domain
. Consider the sign domain
 in Fig. 3 and let us denote by \(\alpha _\texttt{S}:\wp (\mathbb {Z})\rightarrow { Sign}\), and \(\gamma _\texttt{S}\) the function associating with each abstract element the represented set, e.g., \(\gamma _\texttt{S}(\mathbb {Z}_{\le 0})=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n\le 0\end{array} \right. \right\} \), and let
in Fig. 3 and let us denote by \(\alpha _\texttt{S}:\wp (\mathbb {Z})\rightarrow { Sign}\), and \(\gamma _\texttt{S}\) the function associating with each abstract element the represented set, e.g., \(\gamma _\texttt{S}(\mathbb {Z}_{\le 0})=\left\{ ~n\in \mathbb {Z} \left| \begin{array}{l}n\le 0\end{array} \right. \right\} \), and let
 . Let
. Let
 and
and
 Then we have that
Then we have that
-
(1)
\(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\), since \({ Sign}{\llbracket \texttt{r} \rrbracket }{ Sign}(\{-10,0,10\})={ Sign}{\llbracket \texttt{r} \rrbracket }\mathbb {Z}={ Sign}(\left\{ ~n \left| \begin{array}{l}n<0\end{array} \right. \right\} )=\left\{ ~n \left| \begin{array}{l}n<0\end{array} \right. \right\} \subsetneq \mathtt {\tau }\);
-
(2)
\({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}{ Sign}(\texttt{c})={\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}{ Sign}(\{-10,0,10\})={\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\mathbb {Z}=\mathbb {Z}_{<0}=\alpha _\texttt{S}(\texttt{d})\lneq _{{\tiny { Sign}}}\mathbb {Z}_{\le 0}\), where trivially \(\mathbb {Z}_{\le 0}=\alpha _\texttt{S}(\mathtt {\tau })\)
But, \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r}_1)_\mathtt {\tau }\) does not hold, since \({ Sign}{\llbracket \texttt{r}_1 \rrbracket }{ Sign}(\{-10,0,10\})={ Sign}{\llbracket \texttt{r}_1 \rrbracket }\mathbb {Z}={ Sign}(\mathbb {Z})=\mathbb {Z}\not \subseteq \mathtt {\tau }\), and therefore we cannot find \(\texttt{d}'\in \wp (\mathbb {Z})\) such that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_1\,\langle \texttt{d}'\rangle \), making not possible to apply rule seq.
The logic above becomes complete if we add/substitute rule (seq) with the following rule computing code semantics

and the rule, with infinite premixes

where \(\texttt{r}^n\) is a syntactic sugar defined as:
 and
and
 . But it is worth noting that in this way the logic itself becomes undecidable requiring to compute a code semantics and to prove infinite conditions for being applied. Let us denote as \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) the derivation in the rule system in Fig. 4 extended with rules seq\(_1\) and iterate\(_1\).
. But it is worth noting that in this way the logic itself becomes undecidable requiring to compute a code semantics and to prove infinite conditions for being applied. Let us denote as \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \) the derivation in the rule system in Fig. 4 extended with rules seq\(_1\) and iterate\(_1\).
Theorem 5
Let \(\texttt{c},\texttt{d}\in \textsf{C}=\wp (\mathbb {M})\), \(\textsf{A}\in { Abs}(\textsf{C})\) (\(\textsf{A}=\gamma \alpha \)), \(\texttt{r}\in {{\,\mathrm{{\mathfrak {L}}}\,}}\), \(\mathtt {\tau }\in \textsf{A}\) and
 . If (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le \alpha (\texttt{d})<\mathtt {\tau }\) then we have \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \).
. If (1) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) and (2) \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le \alpha (\texttt{d})<\mathtt {\tau }\) then we have \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \).
Proof
Let us prove by structural induction on the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\).
\(\texttt{r}=\textsf{e}\): If (1) and (2) hold, then trivially by rule (transfer) we have \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\textsf{e}\,\langle \texttt{d}\rangle \).
\(\texttt{r}=\texttt{r}_1\oplus \texttt{r}_2\): Let us consider condition (2), if \({\llbracket \texttt{r}_1\oplus \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) then we have that \({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\vee _{\!\!{\tiny \textsf{A}}}{\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), implying that we have both the relations \({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{Q})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\) and \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{Q})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). By properties of bca, this means that \((\alpha {\llbracket \texttt{r}_1 \rrbracket }\gamma )\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}{\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), but then by Lemma 1 we have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r}_1)_\mathtt {\tau }\). Analogously we also have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r}_2)_\mathtt {\tau }\). Hence, by inductive hypothesis implies that \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_1\,\langle \texttt{d}\rangle \) and \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_2\,\langle \texttt{d}\rangle \), and therefore, by rule (join) we have that \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{d}\rangle \), being \(\alpha (\texttt{d}\vee \texttt{d})=\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\).
\(\texttt{r}=\texttt{r}_1;\texttt{r}_2\): Suppose \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) together with \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha (\texttt{c}))\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). First of all let us observe that, by definition \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha (\texttt{c}))={\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha (\texttt{c})))\). Then, by monotonicity and by construction of abstract semantics we have
which is condition (2) for the hypothesis of rule (seq\(_1\)). As far as (1) is concerned let us observe that
where the last holds by definition of \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\), and for what we have proved above we have
Finally, by Lemma 1 it must be \(\gamma ({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha {\llbracket \texttt{r}_1 \rrbracket }\gamma \alpha (\texttt{c})))\subsetneq \mathtt {\tau }\), since we proved above that \({\llbracket \texttt{r}_2 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha {\llbracket \texttt{r}_1 \rrbracket }\gamma \alpha (\texttt{c}))\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). Therefore we have (1), i.e., \(\textsf{A}{\llbracket \texttt{r}_2 \rrbracket }\textsf{A}({\llbracket \texttt{r}_1 \rrbracket }\gamma \alpha (\texttt{c}))\subsetneq \mathtt {\tau }\). At this point, by inductive hypothesis we conclude that \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle {\llbracket \texttt{r}_1 \rrbracket }\gamma \alpha (\texttt{c})\rangle \,\texttt{r}_2\,\langle \texttt{d}\rangle \), and by rule (seq\(_1\)) we derive \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_1;\texttt{r}_2\,\langle \texttt{d}\rangle \).
\(\texttt{r}=\texttt{r}_1^*\): Suppose \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\) together with \({\llbracket \texttt{r} \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}(\alpha (\texttt{c}))\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). By definition of abstract semantics, we have \(\bigvee _{\!\!{\tiny \textsf{A}}}({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\alpha (\texttt{c})={\llbracket \texttt{r}_1^* \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\), which implies, by definition of least upper bound, that for all n, we have \(({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\alpha (\texttt{c})\le _{{\tiny \textsf{A}}}\alpha (\texttt{d})\lneq _{{\tiny \textsf{A}}}\mathtt {\tau _\alpha }\). As before, we can also show that
since, by induction and by definition, we can observe that \({\llbracket \texttt{r}_1^n \rrbracket }^{\sharp }_{{\tiny \textsf{A}}}=({\llbracket \texttt{r}_1 \rrbracket }^{\sharp }_{{\tiny \textsf{A}}})^n\). Now, by Lemma 1 we also have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r}_1^n)_\mathtt {\tau }\) for each \(n\in \mathbb {N}\), hence by inductive hypothesis we have that \(\forall n\in \mathbb {N}.\,\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_1^n\,\langle \texttt{d}\rangle \). Finally, by rule (iterate\(_1\)) we have that \(\mathtt {\tau }\vDash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}_1^*\,\langle \texttt{d}\rangle \).
Let us consider some simple examples of derivation. For the sake of simplicity, since the following programs have only one variable x, we abuse notation identifying the domain of stores \(\mathbb {M}\) with the domain of values \(\mathbb {Z}\). Hence, in the following examples, we will define \(\textsf{A}\) directly on \(\wp (\mathbb {Z})\).
Example 4
Let us consider the regular command in \(\textrm{Reg}\)

and \(\mathtt {\tau }=\top \). Let us consider the abstract domain \(\textsf{A}={ Sign}\) (let \(\textsf{A}=\gamma _{\texttt{S}}\alpha _{\texttt{S}}\)) on the left of Fig. 3. For the sake of readability, in the following we identify each abstract element with its meaning, e.g., \(\mathbb {Z}_{\le 0}\) with \(\{n~|~n\le 0\}\). As observe previously, both the boolean expressions in \(\texttt{r}\) are expressible (and therefore quasi-expressible) in \({ Sign}\), since \(x\le 0\) is expressed by \(\mathbb {Z}_{\le 0}\) and \(0\le x\) by \(\mathbb {Z}_{\ge 0}\). By Theorem 1 we have that both \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{{\tiny \texttt{d}}}(x\le 0?)\) and \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{{\tiny \texttt{d}}}(0<x?)\) hold for any \(\texttt{d}\). Let us consider an input property
 (\({ Sign}(\texttt{c})=\mathbb {Z}_{\le 0}\)), then \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(x\le 0?)\) and therefore by rule (transfer):
(\({ Sign}(\texttt{c})=\mathbb {Z}_{\le 0}\)), then \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(x\le 0?)\) and therefore by rule (transfer):

being \({\llbracket x\le 0? \rrbracket }{ Sign}(\texttt{c})={\llbracket x\le 0? \rrbracket }\mathbb {Z}_{\le 0}=\mathbb {Z}_{\le 0}\).
Now, note that \({ Sign}\,{\llbracket x:=x*2 \rrbracket }\,{ Sign}(\mathbb {Z}_{\le 0})={ Sign}\,{\llbracket x:=x*2 \rrbracket }\,\mathbb {Z}_{\le 0}=\mathbb {Z}_{\le 0}\subsetneq \top \), hence \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\mathbb {Z}_{\le 0}}(x:=x*2)\), and therefore we can apply again rule (transfer)

since \({\llbracket x:=x*2 \rrbracket }{ Sign}(\mathbb {Z}_{\le 0})=\mathbb {Z}_{\le 0}\). Finally by rule (seq)

Now, we can apply rule (iterate) obtaining

Finally, by Theorem 1 we have \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(0\le x?)\), implying again by rule (transfer)

since \({\llbracket 0\le x \rrbracket }{ Sign}(\texttt{c})={\llbracket 0\le x \rrbracket }\mathbb {Z}_{\le 0}=\mathbb {Z}_{=0}\) In this way we can conclude, by rule (seq), that \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}\rangle \,(x\le 0?;x:=x*2)^*;0\le x?\,\langle \mathbb {Z}_{=0}\rangle \), meaning that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})\).
Example 5
Let us consider the regular program
 , where
, where

Let us consider as abstract domain \(\textsf{A}={ Int}\) (let \(\textsf{A}=\gamma _{{i}}\alpha _{{i}}\)), \(\mathtt {\tau }=\gamma _{{i}}([0,+\infty ])\) and
 (\(\alpha _{{i}}(\texttt{c})=[0,30]\)). In the following, for the sake of readability, we identify [n, m] with its meaning \(\{i~|~n\le i\le m\}\). As already observed, in the considered abstract domain \(0<x\) is expressible w.r.t. \(\mathtt {\tau }\), while \(x<100\) is not. By Theorem 1, we have \(\forall \texttt{d}\in \textsf{C}\) that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{d}}(0<x?)_\mathtt {\tau }\) while we have that \(\forall \texttt{d}\subsetneq \mathtt {\tau }\) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{d}}(x<100?)_\mathtt {\tau }\), since \({ Int}({\llbracket x<100? \rrbracket }\texttt{d})\subseteq [0,100]\subsetneq \mathtt {\tau }\).
(\(\alpha _{{i}}(\texttt{c})=[0,30]\)). In the following, for the sake of readability, we identify [n, m] with its meaning \(\{i~|~n\le i\le m\}\). As already observed, in the considered abstract domain \(0<x\) is expressible w.r.t. \(\mathtt {\tau }\), while \(x<100\) is not. By Theorem 1, we have \(\forall \texttt{d}\in \textsf{C}\) that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{d}}(0<x?)_\mathtt {\tau }\) while we have that \(\forall \texttt{d}\subsetneq \mathtt {\tau }\) \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{d}}(x<100?)_\mathtt {\tau }\), since \({ Int}({\llbracket x<100? \rrbracket }\texttt{d})\subseteq [0,100]\subsetneq \mathtt {\tau }\).
Let us consider \(\texttt{r}_1\) first. By rule (transfer)

Now we have that \({\llbracket x:=x-1 \rrbracket }{ Int}([1,30])=[0,29]\), hence again by rule (transfer) we derive

being \({ Int}({\llbracket x:=x-1 \rrbracket }{ Int}([1,30])[0,29]\subsetneq \mathtt {\tau }\), and therefore by rule (seq) we have \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}\rangle \,0<x?;x:=x-1\,\langle [0,29]\rangle \). Now, by rule (iterate), we prove

Let us consider \(\texttt{r}_2\). By rule (transfer)

Now we have that \({\llbracket x:=x+1 \rrbracket }[0,30])=[1,31]\), hence again by rule (transfer) we derive \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}\rangle \,x:=x+1\,\langle [1,31]\rangle \), and therefore \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}\rangle \,x<100?;x:=x+1\,\langle [1,31]\rangle \) by rule (seq). In this case, unfortunately \({ Int}([1,31])=[1,31]\not \subseteq { Int}(\texttt{c})=[1,30]\), hence we cannot apply rule (iterate). Let us consider, instead
 (\({ Int}(\texttt{c}')=[0,100]\)). Then by rule (transfer)
(\({ Int}(\texttt{c}')=[0,100]\)). Then by rule (transfer)

then being \({\llbracket x:=x+1 \rrbracket }[0,99])=[1,100]\), we have by rule (transfer)

and therefore \(\vdash _{{\!\tiny \textsf{A}}}\langle \texttt{c}'\rangle \,x<100?;x:=x+1\,\langle [1,100]\rangle \) by rule (seq). Now by rule (iterate)

At this point, by rule (relax\(_2\))

and therefore we can apply rule (join)

since \(\texttt{c}\cup \texttt{c}'=\texttt{c}'\), meaning that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_\mathtt {\tau }\).
Example 6
In this example, we show that we can derive limits also for diverging loops. Consider \(\texttt{r}=(x\le 0?;x:=2*x)^*\), \(\textsf{A}={ Int}\) (let \(\textsf{A}=\gamma _{{i}}\alpha _{{i}}\)) and
 . In this case we can observe that if we start from a finite \(\texttt{c}\) then it is not possible to apply rule iterate since we enlarge at least one bound of the interval, while if we compute adequacy on a point including the limit we can prove adequacy.
. In this case we can observe that if we start from a finite \(\texttt{c}\) then it is not possible to apply rule iterate since we enlarge at least one bound of the interval, while if we compute adequacy on a point including the limit we can prove adequacy.
Let \(\texttt{c}\) be such that \(\alpha _{{i}}(\texttt{c})=[n,0]\subsetneq [-\infty ,0]\), then \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,x\le 0?\,\langle \texttt{c}\rangle \), while \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,x:=2*x\,\langle \texttt{d}\rangle \) with \(-2n\in \texttt{d}\), hence \(\alpha _{{i}}(\texttt{d})\not \subseteq \alpha _{{i}}(\texttt{c})\). It is trivial to observe that the only case in which we obtain a result contained in the starting point \(\texttt{c}\) is when \(\texttt{c}=[-\infty ,n]\) (\(n\le 0\)), since in this case we can derive, in the proof system, that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,x:=2*x\,\langle \texttt{d}\rangle \) with \(\texttt{d}\subseteq [-\infty ,2n]\subseteq [-\infty ,n]\).
Let, for instance \(n=-10\), then trivially \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle [-\infty ,-10]\rangle \,x\le 0?\,\langle [-\infty ,-10]\rangle \), \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle [-\infty ,-10]\rangle \,x:=2*x\,\langle [-\infty ,-20]\rangle \), hence, by using the composition rule, we prove \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle [-\infty ,-10]\rangle \,x\le 0?;x:=2*x\,\langle [-\infty ,-20]\rangle \) and being \([-\infty ,-20]\subseteq [-\infty ,-10]\), we can derive \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle [-\infty ,-10]\rangle \,x\le 0?;x:=2*x\,\langle [-\infty ,-10]\rangle \). Hence, \(\forall \texttt{c}\in \left\{ ~[-\infty ,n] \left| \begin{array}{l}n<0\end{array} \right. \right\} \) we have that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}(\texttt{r})_{[-\infty ,0]}\).
Example 7
Let us consider the regular command in \(\textrm{Reg}\)

supposing to add to the language the operator \({ even}(x)\) returning true if x is even, false otherwise, with \(\textsf{A}={ Int}\) (let \(\textsf{A}=\gamma _{{i}}\alpha _{{i}}\)) and \(\mathtt {\tau }=\top \). It should be clear that \({ even}(x)\) is not quasi-expressible in \(\textsf{A}\), however we can prove adequacy on some points \(\texttt{c}\). Let \(\texttt{c}=[n,+\infty ]\), with \(n>0\), then we have that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,{ even}(x)?\,\langle \texttt{c}\cap 2\mathbb {Z}\rangle \), since we can trivially prove that \(\widetilde{\mathbb {C}}^{{\tiny \textsf{A}}}_{\texttt{c}}({ even}(x))_\mathtt {\tau }\). At this point, it holds that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\cap 2\mathbb {Z}\rangle \,x:=x+1\,\langle [n+1,+\infty ]\cap 2\mathbb {Z}+1\rangle \) by rule (transfer). Hence, by rule (seq) we have \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,{ even}(x);x:=x+1\,\langle [n+1,+\infty ]\cap 2\mathbb {Z}+1\rangle \), and being \(n>0\) we have \(\texttt{d}=[n+1,+\infty ]\subseteq [n,+\infty ]\) meaning that \(\alpha _{{i}}(\texttt{d}\cap 2\mathbb {Z}+1)=\texttt{d}\subseteq \alpha _{{i}}(\texttt{c})=\texttt{c}\), and therefore \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,({ even}(x)?;x:=x+1)^*\,\langle \texttt{c}\rangle \), rule (seq) and by rule (iterate).
On the other hand, \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\lnot { even}(x)?\,\langle \texttt{c}\cap 2\mathbb {Z}+1\rangle \), while \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\cap 2\mathbb {Z}+1\rangle \,x:=2x\,\langle [2n,+\infty ]\cap 2\mathbb {Z}\rangle \), both by rule (transfer), with \([n,+\infty ]\supseteq [2n,+\infty ]\).
Finally, we have that \(\texttt{c}\cup ([2n,+\infty ]\cap 2\mathbb {Z})=[n,+\infty ]\cup ([2n,+\infty ]\cap 2\mathbb {Z})=\texttt{c}\), which means that \(\alpha _{{i}}(\texttt{c})=[n,+\infty ]\subsetneq \mathtt {\tau }\). Then we conclude, by rule (join), that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,\texttt{r}\,\langle \texttt{c}\rangle \), i.e., adequacy w.r.t. \(\tau \) is satisfied.
Example 8
Let us consider a final example with a relational domain such that Octagons [25, 26] for the regular command in \(\textrm{Reg}\)

with \(\textsf{A}={ Oct}\) (let \(\textsf{A}=\gamma _\texttt{O}\alpha _\texttt{O}\)) and \(\mathtt {\tau }=\{x\le 5,y\le 7\}\). In this case, the guard is quasi-expressible. Let us consider
 . By Theorem 1, we have \(\forall \texttt{d}\in \textsf{C}\) that
. By Theorem 1, we have \(\forall \texttt{d}\in \textsf{C}\) that
 , hence, by rule (transfer), \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,y-x\le 0?\,\langle \{y\le 2,x\le 1,y-x\le 0\}\rangle \). Then, by rule (transfer) we have also that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \{y\le 2,x\le 1,y-x\le 0\}\rangle \,y:=y-1\,\langle \{y\le 1,x\le 1,y-x\le -1\}\rangle \) and by rule (seq) we have \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,y-x\le 0?;y:=y-1\,\langle \{y\le 1,x\le 1,y-x\le -1\}\rangle \) (Fig. 5). Then, since \(\{y\le 2,x\le 1,y-x\le -1\}\le _{{\tiny \textsf{A}}}\texttt{c}\), we can apply rule (iterate) obtaining \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,(y-x\le 0?;y:=y-1)^*\,\langle \texttt{c}\rangle \).
, hence, by rule (transfer), \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,y-x\le 0?\,\langle \{y\le 2,x\le 1,y-x\le 0\}\rangle \). Then, by rule (transfer) we have also that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \{y\le 2,x\le 1,y-x\le 0\}\rangle \,y:=y-1\,\langle \{y\le 1,x\le 1,y-x\le -1\}\rangle \) and by rule (seq) we have \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,y-x\le 0?;y:=y-1\,\langle \{y\le 1,x\le 1,y-x\le -1\}\rangle \) (Fig. 5). Then, since \(\{y\le 2,x\le 1,y-x\le -1\}\le _{{\tiny \textsf{A}}}\texttt{c}\), we can apply rule (iterate) obtaining \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,(y-x\le 0?;y:=y-1)^*\,\langle \texttt{c}\rangle \).
Now, also \(x-y\le 0\) is expressible, hence we have that, by rule (transfer), \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,x-y\le 0?\,\langle \{y\le 2,x\le 1,x-y\le 0,y-x\le 2\}\rangle \), Hence, we can prove that \(\mathtt {\tau }\vdash _{{\!\tiny \textsf{A}}}\!\langle \texttt{c}\rangle \,(y-x\le 0?;y:=y-1)^*;x-y\le 0?\,\langle \{y\le 2,x\le 1,x-y\le 0,y-x\le 2\}\rangle \), again by rule (seq), and therefore we prove adequacy on \(\texttt{c}\).
Graphical representation of octagons in Example 8
6 Conclusions
We introduced the novel notion of adequate abstract domain together with a refinement strategy to adjust abstract domains to make them adequate and a program logic to check whether the abstract interpretation designed on a given abstract domain is adequate. Our program logic is simple and can be checked online during program analysis.
Adequacy is particularly interesting when we are interested to prove whether our abstract interpreter incorporates enough information (here encoded by the bound \(\mathtt {\tau }\)) in the computed invariant. This can have applications beyond program analysis, for instance in language-based security and code protection. In language-based security, as specified by abstract non-interference [15, 21, 23], adequacy could guarantee that certain amount of information is kept secret or dually it is released in the case of declassification, and this could be analyzed also for dynamic code [1, 24]. In code protection the notion of adequacy become stronger than completeness. The standard approach to protect code against program analysis is to make the abstract interpreter maximally imprecise with respect to the given program, which means incomplete [16, 18, 22]. In this case we may replace completeness with adequacy, and imagine code protecting transformations making an abstract interpreter inadequate for the transformed code. When the chosen bound is \(\top \) this corresponds to have a code transformation for which the abstract interpreter is totally blind and cannot extract any meaningful information. Finally, for program verification, it could be interesting to exploit the idea introduced for partial completeness [7], i.e., the use of a metric for weakening completeness, for strengthening adequacy by fixing a maximal distance that we want to guarantee from the fixed bound \(\tau \).
Notes
- 1.
By \(\le _{{\tiny \textsf{A}}}\) we denote the partial order relation on \(\textsf{A}\).
- 2.
Similarly to what happens with completeness, adequacy of any sound abstract operator implies the adequacy of the best correct approximation.
- 3.
Where \(\textsf{max}\) extracts the upper bounds from a set.
- 4.
Let us recall that \(\mathcal{M}\) is the Moore closure, namely the operator closing a set by concrete greatest lower bound, hence making a set a Moore family.
- 5.
 is introduced by \(\boxplus \) in \({ Sign}''\).
is introduced by \(\boxplus \) in \({ Sign}''\).
References
Arceri, V., Mastroeni, I.: Analyzing dynamic code: a sound abstract interpreter for evil eval. ACM Trans. Priv. Secur. 24(2), 10:1–10:38 (2020)
Bourdoncle, F.: Abstract interpretation by dynamic partitioning. J. Funct. Program. 2(4), 407–435 (1992)
Bruni, R., Giacobazzi, R., Gori, R., Garcia-Contreras, I., Pavlovic, D.: Abstract extensionality: on the properties of incomplete abstract interpretations. Proc. ACM Program. Lang. 4(POPL), 28:1–28:28 (2020). https://doi.org/10.1145/3371096
Bruni, R., Giacobazzi, R., Gori, R., Ranzato, F.: A logic for locally complete abstract interpretations. In: Symposium on Logic in Computer Science, LICS, pp. 1–13. IEEE (2021)
Bruni, R., Giacobazzi, R., Gori, R., Ranzato, F.: Abstract interpretation repair. In: Jhala, R., Dillig, I. (eds.) PLDI 2022: 43rd ACM SIGPLAN International Conference on Programming Language Design and Implementation, San Diego, CA, USA, 13–17 June 2022, pp. 426–441. ACM (2022)
Bruni, R., Giacobazzi, R., Gori, R., Ranzato, F.: A correctness and incorrectness program logic. J. ACM 70(2), 1–45 (2023)
Campion, M., Preda, M.D., Giacobazzi, R.: Partial (in)completeness in abstract interpretation: limiting the imprecision in program analysis. Proc. ACM Program. Lang. 6(POPL), 1–31 (2022). https://doi.org/10.1145/3498721
Cousot, P.: Asynchronous iterative methods for solving a fixed point system of monotone equations in a complete lattice. Res. rep. R.R. 88, Laboratoire IMAG, Université scientifique et médicale de Grenoble, p. 15 Grenoble, France (1977)
Cousot, P.: Constructive design of a hierarchy of semantics of a transition system by abstract interpretation. Theor. Comput. Sci. 277(1–2), 47–103 (2002)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Conference Record of the 4th ACM Symposium on Principles of Programming Languages ( POPL 1977), pp. 238–252. ACM Press (1977)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: Conference Record of the 6th ACM Symposium on Principles of Programming Languages ( POPL 1979), pp. 269–282. ACM Press (1979)
Cousot, P., Cousot, R.: Comparing the Galois connection and widening/narrowing approaches to abstract interpretation. In: Bruynooghe, M., Wirsing, M. (eds.) PLILP 1992. LNCS, vol. 631, pp. 269–295. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55844-6_142
Cousot, P.: Principles of Abstract Interpretation. MIT Press, Cambridge (2021)
Filé, G., Giacobazzi, R., Ranzato, F.: A unifying view of abstract domain design. ACM Comput. Surv. 28(2), 333–336 (1996)
Giacobazzi, R., Mastroeni, I.: Adjoining classified and unclassified information by abstract interpretation. J. Comput. Secur. 18(5), 751–797 (2010)
Giacobazzi, R., Mastroeni, I.: Making abstract interpretation incomplete: modeling the potency of obfuscation. In: Miné, A., Schmidt, D. (eds.) SAS 2012. LNCS, vol. 7460, pp. 129–145. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33125-1_11
Giacobazzi, R., Ranzato, F., Scozzari, F.: Making abstract interpretation complete. J. ACM 47(2), 361–416 (2000)
Giacobazzi, R., Jones, N.D., Mastroeni, I.: Obfuscation by partial evaluation of distorted interpreters. In: Kiselyov, O., Thompson, S.J. (eds.) Proceedings of the ACM SIGPLAN 2012 Workshop on Partial Evaluation and Program Manipulation, PEPM 2012, Philadelphia, Pennsylvania, USA, 23–24 January 23–24 2012, pp. 63–72. ACM (2012)
Giacobazzi, R., Logozzo, F., Ranzato, F.: Analyzing program analyses. In: Rajamani, S.K., Walker, D. (eds.) Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, 15–17 January 2015, pp. 261–273. ACM (2015)
Giacobazzi, R., Mastroeni, I.: Making abstract models complete. Math. Struct. Comput. Sci. 26(4), 658–701 (2016)
Giacobazzi, R., Mastroeni, I.: Abstract non-interference: a unifying framework for weakening information-flow. ACM Trans. Priv. Secur. 21(2), 1–31 (2018)
Giacobazzi, R., Mastroeni, I., Preda, M.D.: Maximal incompleteness as obfuscation potency. Formal Aspects Comput. 29(1), 3–31 (2017)
Mastroeni, I.: Abstract interpretation-based approaches to security - A survey on abstract non-interference and its challenging applications. In: Banerjee, A., Danvy, O., Doh, K., Hatcliff, J. (eds.) Semantics, Abstract Interpretation, and Reasoning about Programs: Essays Dedicated to David A. Schmidt on the Occasion of his Sixtieth Birthday, Manhattan, Kansas, USA, 19–20th September 2013. EPTCS, vol. 129, pp. 41–65 (2013)
Mastroeni, I., Arceri, V.: Improving dynamic code analysis by code abstraction. In: Lisitsa, A., Nemytykh, A.P. (eds.) Proceedings of the 9th International Workshop on Verification and Program Transformation, VPT@ETAPS 2021, Luxembourg, Luxembourg, 27th and 28th of March 2021. EPTCS, vol. 341, pp. 17–32 (2021)
Minè, A.: The octagon abstract domain. In: AST 2001 in WCRE 2001. pp. 310–319. IEEE, IEEE CS Press (2001)
Miné, A.: The octagon abstract domain. Higher Order Symbol. Comput. 19(1), 31–100 (2006). https://doi.org/10.1007/s10990-006-8609-1
Müller, M.N., Fischer, M., Staab, R., Vechev, M.: Abstract interpretation of fixpoint iterators with applications to neural networks. Proc. ACM Program. Lang. 7(PLDI), 786–810 (2023)
O’Hearn, P.W.: Incorrectness logic. Proc. ACM Program. Lang. (POPL) 4(10), 1–32 (2020)
Winskel, G.: The Formal Semantics of Programming Languages: An Introduction. MIT press, Cambridge (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Giacobazzi, R., Mastroeni, I., Perantoni, E. (2023). How Fitting is Your Abstract Domain?. In: Hermenegildo, M.V., Morales, J.F. (eds) Static Analysis. SAS 2023. Lecture Notes in Computer Science, vol 14284. Springer, Cham. https://doi.org/10.1007/978-3-031-44245-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-031-44245-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-44244-5
Online ISBN: 978-3-031-44245-2
eBook Packages: Computer ScienceComputer Science (R0)







 and
and


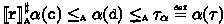 .
.
 ).
).
 is introduced by
is introduced by