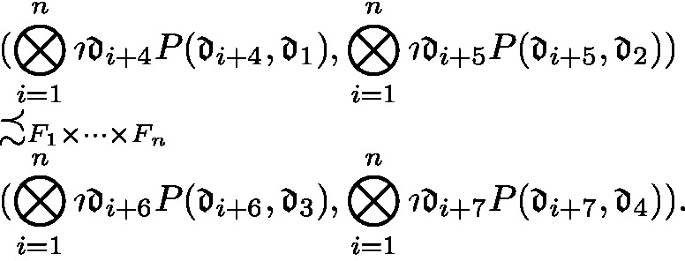Abstract
The problem of particulars and universals is one of the most essential problems in the formal philosophy of language in the sense that it consists in a crossroads of ontology and semantics. According to Resemblance Nominalism, resemblance relations are primitive and the properties of a thing are defined by them. We (2020) proposed, in terms of measurement theory, a first-order modal resemblance logic \(\textsf{MRL}\) that can furnish solutions to the problems with which Resemblance Nominalism is confronted. Yi (2014) raises a new version of degree of resemblance problem with Resemblance Nominalism of Rodriguez-Pereyra (2002). We think this problem to be a problem of multidimensionality. When we considered this problem, we realized that the model of \(\textsf{MRL}\) was not able to deal appropriately with the multidimensionality of this type of problem. The aim of this paper is to revise \(\textsf{MRL}\) so that the revised first-order modal resemblance logic \(\textsf{RMRL}\) can solve Rodriguez-Pereyra-Yi Problem in terms of measurement-theoretic multidimensional representation. Measurement theory makes it possible that qualitative resemblance relations can represent quantitative (numerical) functions, whereas it is not designed to explicate the parthood between a particular and its parts referred to for determining the raking on a resemblance relation. So, in the construction of the multidimensional model of \(\textsf{RMRL}\), we connect measurement-theory with mereology that can explicate the parthood between a particular and its parts referred to for determining the raking on a resemblance relation. The punch line of Resemblance Nominalism is the reducibility of universals into resemblance relations. The point of formalizing Resemblance Nominalism in \(\textsf{RMRL}\) is to avoid the circularity in this reduction into which it tends to slide.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- first-order logic
- formal philosophy of language
- measurement theory
- mereology
- model theory
- multidimensionality
- nominalism
- ontology
- particulars
- Platonism
- realism
- resemblance relation
- resemblance nominalism
- universals
1 Motivation
The problem of particulars and universals is one of the most essential problems in the formal philosophy of language in the sense that it consists in a crossroads of ontology and semantics: When we translate a natural language into a first-order (modal) language, (though it is a problem which formal language we should adopt in this translation), the semantic problem as to which entity we should choose as the semantic value of a symbol in the model of first-order modal logic depends crucially on the ontological problem as to which ontology we should adopt. According to Rodriguez-Pereyra [5], there are at least two kinds of Nominalism: one that maintains that there are no universals and the other that maintains that there are no abstract objects like classes, functions, numbers and possible worlds. On the other hand, Realism about universals is the doctrine that there are universals, and Platonism about abstract objects is the doctrine that there are abstract objects. The doctrines about universals and the doctrines about abstract objects are independent. Nominalisms about universals can be classified into at least eight types: Trope Theory, Predicate Nominalism, Concept Nominalism, Ostrich Nominalism, Mereological Nominalism, Class Nominalism, Resemblance Nominalism, and Causal Nominalism.Footnote 1 In this paper we focus on Resemblance Nominalism. Rodriguez-Pereyra [4] is the most frequently mentioned work in the field of Resemblance Nominalism. As Rodriguez-Pereyra [5] argues, according to Resemblance Nominalism, it is not because things are scarlet that they resemble one another, but what makes them scarlet is that they resemble one another. Resemblance relations are primitive and the properties of a thing are defined by resemblance relations. Resemblance Nominalism reifies neither resemblance relations nor accessibility relations in themselves. Resemblance Nominalism in general is confronted with at least seven problems: Imperfect Community Problem, Companionship Problem, Mere Intersections Problem, Contingent Coextension Problem, Necessary Coextension Problem, Infinite Regress Problem, and Degree of Resemblance Problem.Footnote 2 We [8] proposed, in terms of measurement theory, a first-order modal resemblance logic \(\textsf{MRL}\) that can furnish solutions to all of these problems. Yi [10] raises a version of degree of resemblance problem. Yi [10, pp.622-625] argues as follows:
(1) Carmine resembles vermillion more than it resembles triangularity.
(2) is a resemblance-nominalistic formulation that expresses what makes (1) true:
(2) Some carmine particular resembles some vermillion particular more closely than any carmine particular resembles any triangular particular.
Rodriguez-Pereyra [4, p.65] defines the degree of resemblance as follows :
Definition 1
(Degree of Resemblance). The particulars resemble to the degree n iff they share n properties.
By “properties”, Rodriguez-Pereyra means sparse properties. Rodriguez-Pereyra [4, p.20,pp.50-52] adopts the following Lewis [2]’s distinction between abundant and sparse properties:
[The abundant properties] pay no heed to the qualitative joints, but carve things up every which way. Sharing them has nothing to do with similarity [(resemblance)] ...There is one of them for any condition we could write down, even if we could write at infinite length and even if we could name all those things that must remain nameless because they fall outside our acquaintance. [They] are as abundant as the sets themselves, because for any whatever, there is the property of belonging to that set ...The sparse properties are another story. Sharing of them makes for qualitative similarity [(resemblance)], they carve at the joints, they are intrinsic, they are highly specific, the sets of their instances are ipso facto not miscellaneous, they are only just enough of them to characterise things completely sand without redundancy.[2, pp. 59-60]
In this paper, we use “properties” in this sense of sparse properties as well as Rodriguez-Pereyra. Under Definition 1, (2) compares the maximum degrees of resemblance. But (2) is false because a possible carmine particular completely resembles a possible triangular particular. For the same particular might be both carmine and triangular. Rodriguez-Pereyra [6] responses to Yi by replacing (2) by (3):
(3) Some carmine particular resembles some triangular particular less closely than any carmine particular resembles any vermillion particular.
Again under Definition 1, (3) compares the minimum degrees of resemblance. Rodriguez-Pereyra [6, p.225] argues that (3) is true because the minimum degree to which a carmine particular can resemble a triangular particular (degree 0) is smaller than the minimum degree to which a carmine particular can resemble a vermillion particular (a degree greater than 0). Yi [11, p.796] criticizes this Rodriguez-Pereyra’s response by arguing that it rests on a false assumption: the minimum degree to which a carmine particular can resemble a vermillion particular is greater than 0. For, on Rodriguez-Pereyra’s notion of resemblance, a carmine particular cannot resemble a vermillion particular unless they share a sparse property, but they might not share any such property. A carmine particular and a vermillion particular might share no non-color sparse property, and two such particulars share also no color sparse property because they have different determinate color properties (i.e., carminity and vermillionity). Although they share determinable color properties (e.g., red), this does not help because, in Rodriguez-Pereyra’s view, determinable properties are not sparse properties. So the minimum degree to which a carmine particular can resemble a vermillion particular might be 0. No doubt this argument by Yi needs examining in detail, but we can safely say that the main culprit of this Rodriguez-Pereyra-Yi Problem is Definition 1 on which both (2) and (3) are based. We consider this problem to be a problem of multidimensionality (such three dimensionality as carminity, vermillionity and triangularity) that requires quantitative (numerical) representations because we cannot have computational method of aggregation only in terms of qualitative resemblance relations. When we considered this problem, we realized that the model of \(\textsf{MRL}\) was not able to deal appropriately with the multidimensionality of this type of problem. The aim of this paper is to revise \(\textsf{MRL}\) so that the revised first-order modal resemblance logic \(\textsf{RMRL}\) can solve Rodriguez-Pereyra-Yi Problem in terms of measurement-theoretic multidimensional representation.Footnote 3 Measurement theory makes it possible that qualitative resemblance relations can represent quantitative (numerical) functions, whereas it is not designed to explicate the parthood between a particular and its parts (referred to for determining the raking on a resemblance relation). So, in the construction of the multidimensional model of \(\textsf{RMRL}\), we would like to connect measurement-theory with mereologyFootnote 4 that can explicate the parthood between a particular and its parts referred to for determining the raking on a resemblance relation. The punch line of Resemblance Nominalism is the reducibility of universals into resemblance relations. The point of formalizing Resemblance Nominalism in \(\textsf{RMRL}\) is to avoid the circularity in this reduction into which it tends to slide. In this paper, we try to give a solution to Rodriguez-Pereyra-Yi Problem by defining in \(\textsf{RMRL}\) the degree of unresemblance (Definition 20), instead of using Definition 1 (on which both (2) and (3) are based) that is the main culprit of this problem so that, in the multidimensional comparison of unresemblance of (1),
the weighted sum of the degrees of unresemblance of carmine particulars to triangular particulars may be greater than that of carmine particulars to vermillion particulars.
In so doing, \(\textsf{RMRL}\) obtains the capacity to deal with multidimensionality in general beyond Rodriguez-Pereyra-Yi Problem. In the semantics of \(\textsf{RMRL}\), a resemblance relation is primitive and the degree of unresemblance is defined in Definition 20 by it via Representation Theorem (Theorem 3) and Uniqueness Theorem (Theorem 4).
The structure of this paper is as follows. In Subsect. 2.1, we define the language \(\mathscr {L}\) of \(\textsf{RMRL}\). In Subsubsect. 2.2.1, we define three measurement-theoretic concepts. In Subsubsect. 2.2.2, we prepare the seven steps to a mereological additive difference factorial proximity structured model \(\mathfrak {M}\) of \(\textsf{RMRL}\). In Subsubsect. 2.2.3, we provide \(\textsf{RMRL}\) with a satisfaction definition relative to \(\mathfrak {M}\), define the truth at \(w\in W\) in \(\mathfrak {M}\), define validity. In Subsubsect. 2.2.4, we show the representation and uniqueness theorems for (multidimensional) resemblance predicates. In Sect. 3, we conclude by giving a solution to Rodriguez-Pereyra-Yi Problem by \(\textsf{RMRL}\).
2 Measurement Theory Meets Meleology in \(\textsf{RMRL}\)
2.1 Language
In this paper, we focus only on the ontology ofproperties that are the sematic values of one-place predicate symbols. So we do not introduce n-place predicate symbols (\(n\ge 2\)) in general into the language of \(\textsf{RMRL}\) the semantic values of which are n-ary relations, though we introduce four-place resemblance predicate symbols indexed by one-place predicate symbols. We define the language \(\mathscr {L}\) of revised first-order modal resemblance logic \(\textsf{RMRL}\):
Definition 2
(Language).
-
Let \(\mathscr {V}\) denote a class of individual variables, \(\mathscr {C}\) a class of individual constants, and \(\mathscr {P}\) a class of one-place predicate symbols.
-
Let \(\leqslant _F\) denote a four-place resemblance predicate symbol indexed by F.
-
When \(n\ge 2\), let \(\leqslant _{F_1\times \cdots \times F_n}\) denote a four-place resemblance predicate symbol indexed by \(F_1,\ldots ,F_n\).
-
The language \(\mathscr {L}\) of \(\textsf{RMRL}\) is given by the following BNF grammar:
$$ \begin{array}{l} t\,\,{:}{:}\!\!=x\ |\ a\\ \varphi \,\,{:}{:}\!\!=F(t)\ |\ t_1=t_2\ |\ \bot \ |\ \lnot \varphi \ |\ \varphi \wedge \psi \ |\ \\ (t_1,t_2)\leqslant _F(t_3,t_4)\ |\ (t_1,t_2)\leqslant _{F_1\times \cdots \times F_n}(t_3,t_4)\ |\ \Box \varphi \ |\ \forall x\varphi , \end{array} $$where \(x\in \mathscr {V}\), \(a\in \mathscr {C}\), and \(F_1,\ldots ,F_n\in \mathscr {P}\).
-
\(\top \), \(\vee \), \(\rightarrow \), \(\leftrightarrow \), \(<_F\), \(<_{F_1\times \cdots \times F_n}\), \(\Diamond \) and \(\exists \) are introduced by the standard definitions.
-
\((t_1,t_2)\leqslant _F(t_3,t_4)\) means that \(t_3\) does not resemble \(t_4\) more than \(t_1\) resembles \(t_2\) with respect to F-ness.
-
When \(n\ge 2\), \((t_1,t_2)\leqslant _{F_1\times \cdots \times F_n}(t_3,t_4)\) means that \(t_3\) does not resemble \(t_4\) more than \(t_1\) resembles \(t_2\) with respect to \(F_1\)-ness and \(\ldots \) and \(F_n\)-ness.
-
The set of all well-formed formulae of \(\mathscr {L}\) is denoted by \(\varPhi _{\mathscr {L}}\).
Remark 1
(Modal Part of \(\textsf{RMRL}\)). In this paper, we do not deal with Contingent Coextension and Necessary Coextension Problems above neither of which relates to multidimensionality that is the main topic of this paper, though we did in [8]. The motivation to introduce a modality \(\Box \) into \(\mathscr {L}\) is only to solve Contingent Coextension and Necessary Coextension Problems.
2.2 Semantics
2.2.1 Three Measurement-Theoretic Concepts
Here we would like to define such measurement-theoretic concepts as
-
1.
scale types,
-
2.
representation and uniqueness theorems, and
-
3.
measurement types
on which the argument of this paper is based: First, according to Roberts [3, pp. 64-69], we classify scale types in terms of the class of admissible transformations \(\varphi \):
Definition 3
(Scale Types).
-
A scale is a triple \((\mathfrak {U},\mathfrak {V},f)\) where \(\mathfrak {U}\) is an observed relational structure that is qualitative, \(\mathfrak {V}\) is a numerical relational structure that is quantitative, and f is a homomorphism from \(\mathfrak {U}\) into \(\mathfrak {V}\).
-
Sometimes we sloppily refer to f alone as a scale.
-
Suppose that \(\mathscr {D}\) is the domain of \(\mathfrak {U}\) and that \(\mathscr {D}'\) is the domain of \(\mathfrak {V}\). Suppose that \(\varphi \) is a function that maps the range of f, the set \(f(\mathscr {D}):=\{f(\mathfrak {d}): \mathfrak {d}\in \mathscr {D}\}\), into \(\mathscr {D}'\). Then the composition \(\varphi \circ f\) is a function from \(\mathscr {D}\) into \(\mathscr {D}'\). If \(\varphi \circ f\) is a homomorphism from \(\mathfrak {U}\) into \(\mathfrak {V}\), we call \(\varphi \) an admissible transformation of scale.
-
When the admissible transformations are all the functions \(\varphi \) of the form \(\varphi (x):=\alpha x; \alpha >0\). \(\varphi \) is called a similarity transformation, and a scale with the similarity transformations as its class of admissible transformations is called a ratio scale.
-
When the admissible transformations are all the functions \(\varphi \) of the form \(\varphi (x):=\alpha x+\beta ; \alpha >0\), \(\varphi \) is called a positive affine transformation, and a corresponding scale is called an interval scale.
-
When the admissible transformations are all the functions \(\varphi \) of the form \(\varphi (x):=\alpha x+\beta ; \alpha \ne 0\), \(\varphi \) is called an affine transformation, and a corresponding scale is called a quasi-interval scale.
-
When a scale is unique up to order, the admissible transformations are monotone increasing functions \(\varphi (x)\), that is, functions \(\varphi (x)\) satisfying the condition that \(x\precsim y\) iff \(\varphi (x)\le \varphi (y)\), where \(\precsim \) is a binary relation on \(\mathscr {D}\). Such a scale is called an ordinal scale.
Example 1
(Mass and Temperature).
-
The measurement of mass is the assignment of a homomorphism f from the observed relational structure \((A,H,\bigcirc )\) (where we judge \(\mathfrak {d}_1\) to be heavier than \(\mathfrak {d}_2\) and the binary operation satisfies \(f(\mathfrak {d}_1\bigcirc \mathfrak {d}_2)=f(\mathfrak {d}_1)+f(\mathfrak {d}_2)\) for any \(\mathfrak {d}_1,\mathfrak {d}_2\in A\)) to the numerical relational structure \((\mathbb {R},>,+)\). Mass is an example of a ratio scale.
-
The measurement of temperature is the assignment of a homomorphism f from the observed relational structure (A, W) (where A is a set of objects and the binary relation \(\mathfrak {d}_1W\mathfrak {d}_2\) holds iff we judge \(\mathfrak {d}_1\) to be warmer than \(\mathfrak {d}_2\)) to the numerical relational structure \((\mathbb {R},>)\). Temperature is an example of an interval scale.
Second, according to Roberts [3, pp. 54-56], we define representation and uniqueness theorems:
Definition 4
(Representation Theorem and Uniqueness Theorem).
-
The first basic problem of measurement theory is the representation problem: Given a numerical relational structure \(\mathfrak {V}\), find conditions on an observed relational structure \(\mathfrak {U}\) (necessary and) sufficient for the existence of a homomorphism f from \(\mathfrak {U}\) to \(\mathfrak {V}\) that preserves all the relations and operations in \(\mathfrak {U}\).
-
The theorem stating conditions on \(\mathfrak {U}\) are (necessary and) sufficient for the existence of f is called a representation theorem.
-
The second basic problem of measurement theory is the uniqueness problem: Find the transformation of the homomorphism f under which all the relations and operations in \(\mathfrak {U}\) are preserved.
-
The theorem stating the type of transformation up to which f is unique is called a uniqueness theorem.
Third, according to Roberts [3, pp. 122-131, pp. 134-142] and Krantz et al., [1, pp. 136-157], we classify measurement types:
Definition 5
(Measurement Types).
-
Suppose \(\mathscr {D}\) is a set, \(\precsim '\) is a binary relation on \(\mathscr {D}\), \(\bigcirc \) is a binary operation on \(\mathscr {D}\), \(\precsim \) is a quaternary relation on \(\mathscr {D}\), and f is a real-valued function.
-
Then we call the representation \(\mathfrak {d}_1\precsim ' \mathfrak {d}_2\) iff \(f(\mathfrak {d}_1)\le f(\mathfrak {d}_2)\), for any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), and \(f(\mathfrak {d}_1\bigcirc \mathfrak {d}_2)=f(\mathfrak {d}_1)+f(\mathfrak {d}_2)\), for any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), extensive measurement.
-
We call the representation \((\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_3,\mathfrak {d}_4)\) iff \(f(\mathfrak {d}_1)-f(\mathfrak {d}_2)\le f(\mathfrak {d}_3)-f(\mathfrak {d}_4)\), for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\), when the direction of differences is taken into consideration, positive-difference measurement, when the direction of differences is not taken into consideration, algebraic-difference measurement.
-
We call the representation \((\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_3,\mathfrak {d}_4)\) iff \(|f(\mathfrak {d}_1)-f(\mathfrak {d}_2)|\le |f(\mathfrak {d}_3)-f(\mathfrak {d}_4)|\) for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\), absolute-difference measurement.
2.2.2 Seven Steps to Construct Model \(\mathfrak {M}\) of \(\textsf{RMRL}\)
By using some measurement-theoretic concepts of Krantz et al. [1] and Suppes et al. [7], we prepare the following seven steps to construct a model \(\mathfrak {M}\) of \(\textsf{RMRL}\):
2.2.2.1 First Step
The first step is a step to prepare an absolute difference structure for the semantics of \(\leqslant _F\) and \(\leqslant _{F_1\times \cdots \times F_n}\). We resort to an absolute difference structure in order to solve the problems of Resemblance Nominalism. Krantz et al. [1, pp.172-173] define an absolute difference structure:
Definition 6
(Absolute Difference Structure). Suppose \(\mathscr {D}\) is a nonempty set and \(\precsim \) a quaternary relation on \(\mathscr {D}\) (binary relation on \(\mathscr {D}\times \mathscr {D}\)). \((\mathscr {D}, \precsim )\) is an absolute difference structure iff, for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4,\mathfrak {d}_1',\mathfrak {d}_2',\mathfrak {d}_3'\in \mathscr {D}\), the following six conditions are satisfied:
-
Condition 1 (Weak Order) \(\precsim \) is a weak order (Connected and Transitive).
-
Condition 2 (Absoluteness) If \(\mathfrak {d}_1\ne \mathfrak {d}_2\), then \((\mathfrak {d}_1,\mathfrak {d}_1)\sim (\mathfrak {d}_2,\mathfrak {d}_2)\prec (\mathfrak {d}_1,\mathfrak {d}_2)\sim (\mathfrak {d}_2,\mathfrak {d}_1)\), where \((\mathfrak {d}_1,\mathfrak {d}_2)\sim (\mathfrak {d}_3,\mathfrak {d}_4):=(\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_3,\mathfrak {d}_4)\) and \((\mathfrak {d}_3,\mathfrak {d}_4)\precsim (\mathfrak {d}_1,\mathfrak {d}_2)\), and \((\mathfrak {d}_1,\mathfrak {d}_2)\prec (\mathfrak {d}_3,\mathfrak {d}_4):=(\mathfrak {d}_3,\mathfrak {d}_4)\not \precsim (\mathfrak {d}_1,\mathfrak {d}_2)\).
-
Condition 3 (Betweenness)
-
1.
If \(\mathfrak {d}_2\ne \mathfrak {d}_3\), \((\mathfrak {d}_1,\mathfrak {d}_2), (\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_1,\mathfrak {d}_3)\), and \((\mathfrak {d}_2,\mathfrak {d}_3), (\mathfrak {d}_3,\mathfrak {d}_4)\precsim (\mathfrak {d}_2,\mathfrak {d}_4)\), then \((\mathfrak {d}_1,\mathfrak {d}_3), (\mathfrak {d}_2,\mathfrak {d}_4)\precsim (\mathfrak {d}_1,\mathfrak {d}_4)\).
-
2.
If \((\mathfrak {d}_1,\mathfrak {d}_2), (\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_1,\mathfrak {d}_3)\) and \((\mathfrak {d}_1,\mathfrak {d}_3), (\mathfrak {d}_3,\mathfrak {d}_4)\precsim (\mathfrak {d}_1,\mathfrak {d}_4)\), then \((\mathfrak {d}_1,\mathfrak {d}_3)\precsim (\mathfrak {d}_1,\mathfrak {d}_4)\).
-
1.
-
Condition 4 (Weak Monotonicity) Suppose that \((\mathfrak {d}_1,\mathfrak {d}_2), (\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_1,\mathfrak {d}_3)\). If \((\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_1',\mathfrak {d}_2')\) and \((\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_2',\mathfrak {d}_3')\), then \((\mathfrak {d}_1,\mathfrak {d}_3)\precsim (\mathfrak {d}_1',\mathfrak {d}_3')\). Moreover if either \((\mathfrak {d}_1,\mathfrak {d}_2)\prec (\mathfrak {d}_1',\mathfrak {d}_2')\) or \((\mathfrak {d}_2,\mathfrak {d}_3)\prec (\mathfrak {d}_2',\mathfrak {d}_3')\), then \((\mathfrak {d}_1,\mathfrak {d}_3)\prec (\mathfrak {d}_1',\mathfrak {d}_3')\).
-
Condition 5 (Solvability) If \((\mathfrak {d}_3,\mathfrak {d}_4)\precsim (\mathfrak {d}_1,\mathfrak {d}_2)\), then there exists \(\mathfrak {d}_4'\in \mathscr {D}\) such that \((\mathfrak {d}_4',\mathfrak {d}_2)\precsim (\mathfrak {d}_1,\mathfrak {d}_2)\) and \((\mathfrak {d}_1,\mathfrak {d}_4')\sim (\mathfrak {d}_3,\mathfrak {d}_4)\).
-
Condition 6 (Archimedean Property) If \(\mathfrak {d}_1^{(1)},\mathfrak {d}_1^{(2)},\ldots ,\mathfrak {d}_1^{(i)},\ldots \) is a strictly bounded standard sequence (i.e., there exist \(\mathfrak {d}_2,\mathfrak {d}_3\in \mathscr {D}\) such that for any \(i=1,2,\ldots \), \((\mathfrak {d}_1^{(i)},\mathfrak {d}_1^{(1)})\precsim (\mathfrak {d}_1^{(i+1)},\mathfrak {d}_1^{(1)})\prec (\mathfrak {d}_2,\mathfrak {d}_3)\) and \((\mathfrak {d}_1^{(1)},\mathfrak {d}_1^{(1)})\prec (\mathfrak {d}_1^{(2)},\mathfrak {d}_1^{(1)})\sim (\mathfrak {d}_1^{(i+1)},\mathfrak {d}_1^{(i)})\)), then the sequence is finite.
The following definition [1, p.172] makes Conditions 3-6 easy to understand.
Definition 7
(Betweenness). Suppose \((\mathscr {D}, \precsim )\) satisfies Conditions 1 and 2 of Definition 6. We say that \(\mathfrak {d}_2\) is between \(\mathfrak {d}_1\) and \(\mathfrak {d}_3\) (in symbols, \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\)) iff \((\mathfrak {d}_1,\mathfrak {d}_2), (\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_1,\mathfrak {d}_3)\).
We can replace Conditions 3-6 by the following Conditions 3’-6’:
-
Condition 3’ (Betweenness)
-
1.
If \(\mathfrak {d}_2\ne \mathfrak {d}_3\), \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\), and \(\mathfrak {d}_2|\mathfrak {d}_3|\mathfrak {d}_4\), then both \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_4\) and \(\mathfrak {d}_1|\mathfrak {d}_3|\mathfrak {d}_4\).
-
2.
If \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\) and \(\mathfrak {d}_1|\mathfrak {d}_3|\mathfrak {d}_4\), then \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_4\).
-
1.
-
Condition 4’ (Weak Monotonicity) If \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\), \(\mathfrak {d}_1'|\mathfrak {d}_2'|\mathfrak {d}_3'\), and \((\mathfrak {d}_1,\mathfrak {d}_2)\sim (\mathfrak {d}_1',\mathfrak {d}_2')\), then \((\mathfrak {d}_2,\mathfrak {d}_3)\precsim (\mathfrak {d}_2',\mathfrak {d}_3')\) iff \((\mathfrak {d}_1,\mathfrak {d}_3)\precsim (\mathfrak {d}_1',\mathfrak {d}_3')\).
-
Condition 5’ (Solvability) If \((\mathfrak {d}_3,\mathfrak {d}_4)\precsim (\mathfrak {d}_1,\mathfrak {d}_2)\) then there exists \(\mathfrak {d}_4'\in \mathscr {D}\) with \(\mathfrak {d}_1|\mathfrak {d}_4'|\mathfrak {d}_2\) and \((\mathfrak {d}_1,\mathfrak {d}_4')\sim (\mathfrak {d}_3,\mathfrak {d}_4)\).
-
Condition 6’ (Archimedean Property) If \(\mathfrak {d}_1^{(i+1)}|\mathfrak {d}_1^{(i)}|\mathfrak {d}_1^{(1)}\) for any \(i=1,2,\ldots \), successive intervals are equal and nonnull, and \((\mathfrak {d}_1^{(i)},\mathfrak {d}_1^{(1)})\) is strictly bounded, then the sequence is finite.
Krantz et al. [1, pp.173-177] prove the following theorems:
Fact 1
(Representation). If \((\mathscr {D}, \precsim )\) is an absolute difference structure, then there exists a real-valued function f on \(\mathscr {D}\) such that, for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\), \((\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_3,\mathfrak {d}_4)\ \text{ iff }\ |f(\mathfrak {d}_1)-f(\mathfrak {d}_2)|\le |f(\mathfrak {d}_3)-f(\mathfrak {d}_4)|\).
Fact 2
(Uniqueness). The above function f is a quasi-interval scale.
2.2.2.2 Second Step
The second step is a step to prepare a basic multidimensional structure for \(\leqslant _{F_1\times \cdots \times F_n}\). Suppes et al. [7, pp. 160-161] define a basic multidimensional comparison structure, called a factorial proximity structure:
Definition 8
(Factorial Proximity Structure).
-
\((\mathscr {D},\precsim )\) is a proximity structure iff the following conditions are satisfied for any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\):
-
\(\precsim \) is a weak order.
-
\((\mathfrak {d}_1,\mathfrak {d}_1)\prec (\mathfrak {d}_1,\mathfrak {d}_2)\) whenever \(\mathfrak {d}_1\ne \mathfrak {d}_2\).
-
\((\mathfrak {d}_1,\mathfrak {d}_1)\sim (\mathfrak {d}_2,\mathfrak {d}_2)\) (Minimality).
-
\((\mathfrak {d}_1,\mathfrak {d}_2)\sim (\mathfrak {d}_2,\mathfrak {d}_1)\) (Symmetricity).
-
-
The structure is called n-factorial iff \(\mathscr {D}:=\displaystyle \prod _{i=1}^{n}\mathscr {D}_i\).
-
We use the expression “\(\mathfrak {d}_1\cdots \mathfrak {d}_n(\in \mathscr {D})\)” for the n-tuple of \(\mathfrak {d}_i\in \mathscr {D}_i\) (\(1\le i\le n\)).
Remark 2
(Motivation to Introduce Mereology into Model of \(\textsf{RMRL}\)). The motivation to introduce mereology into the model \(\mathfrak {M}\) of \(\textsf{RMRL}\) is that the ontological status of this n-tuple \(\mathfrak {d}_1\cdots \mathfrak {d}_n\) is not clear.
2.2.2.3 Third Step
In order to make each dimensional factor the absolute value of a scale difference, we first establish decomposability of a factorial proximity structure \((\mathscr {D},\precsim )\) into each factor \((\mathscr {D}_i,\precsim _i)\) where \(\precsim _i\) is an induced weak order of Definition 10 below. To achieve it, \((\mathscr {D},\precsim )\) must satisfy Betweenness, Restricted Solvability, and the Archimedean Property. In order to define Betweenness, we need One-Factor Independence. Suppes et al. [7, pp.178-181] define these concepts as follows:
Definition 9
(One-Factor Independence). A factorial proximity structure \((\mathscr {D},\precsim )\) satisfies One-Factor Independence iff the following holds for any \(\mathfrak {d}_1,\mathfrak {d}_1',\mathfrak {d}_2,\mathfrak {d}_2',\mathfrak {d}_3,\mathfrak {d}_3',\mathfrak {d}_4,\mathfrak {d}_4'\in \mathscr {D}\): If the two elements in each of the pairs \((\mathfrak {d}_1,\mathfrak {d}_1'),(\mathfrak {d}_2,\mathfrak {d}_2'),(\mathfrak {d}_3,\mathfrak {d}_3'),(\mathfrak {d}_4,\mathfrak {d}_4')\) have identical components on all but one factor, and two elements in each of the pairs \((\mathfrak {d}_1,\mathfrak {d}_3),(\mathfrak {d}_1',\mathfrak {d}_3'),(\mathfrak {d}_2,\mathfrak {d}_4),(\mathfrak {d}_2',\mathfrak {d}_4')\) have identical components on the remaining factor, then
If we consider all pairs whose elements differ with respect to the i th factor only, then one-factor independence asserts that for any \(i (1\le i\le n)\) the induced weak order \(\precsim _i\) on \(\mathscr {D}_i\times \mathscr {D}_i\) of Definition 10 below is independent of the fixed components of the remaining \(\mathscr {D}_i\times \mathscr {D}_i\) for \(j\ne i\).
Definition 10
(Betweenness).
-
Let \((\mathscr {D}:=\prod _{i=1}^{n}\mathscr {D}_i, \precsim )\) be a factorial proximity structure that satisfies One-Factor Independence.
-
Let \(\precsim _i\) denote an induced weak order on \(\mathscr {D}_i\times \mathscr {D}_i\).
-
We say that \(\mathfrak {d}_2\) is between \(\mathfrak {d}_1\) and \(\mathfrak {d}_3\), denoted by \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\), iff
$$ (\mathfrak {d}_1^{(i)},\mathfrak {d}_2^{(i)}),(\mathfrak {d}_2^{(i)},\mathfrak {d}_3^{(i)})\precsim _{i}(\mathfrak {d}_1^{(i)},\mathfrak {d}_3^{(i)})\quad \text{ for } \text{ any } \text{ i }. $$ -
A factorial proximity structure \((\mathscr {D},\precsim )\) satisfies Betweenness iff the following hold for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4,\mathfrak {d}_1',\mathfrak {d}_2',\mathfrak {d}_3'\in \mathscr {D}\):
-
1.
Suppose that \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\) differ on at most one factor, and \(\mathfrak {d}_2\ne \mathfrak {d}_3\), then
-
(a)
if \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\) and \(\mathfrak {d}_2|\mathfrak {d}_3|\mathfrak {d}_4\), then \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_4\) and \(\mathfrak {d}_1|\mathfrak {d}_3|\mathfrak {d}_4\), and
-
(b)
if \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\) and \(\mathfrak {d}_1|\mathfrak {d}_3|\mathfrak {d}_4\), then \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_4\) and \(\mathfrak {d}_2|\mathfrak {d}_3|\mathfrak {d}_4\).
-
(a)
-
2.
Suppose that \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_1',\mathfrak {d}_2',\mathfrak {d}_3'\) differ on at most one factor, \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\), \(\mathfrak {d}_1'|\mathfrak {d}_2'|\mathfrak {d}_3'\), and \((\mathfrak {d}_2,\mathfrak {d}_3)\sim (\mathfrak {d}_2',\mathfrak {d}_3')\), then
$$ (\mathfrak {d}_1,\mathfrak {d}_2)\precsim (\mathfrak {d}_1',\mathfrak {d}_2')\quad \text{ iff }\quad (\mathfrak {d}_1,\mathfrak {d}_3)\precsim (\mathfrak {d}_1',\mathfrak {d}_3'). $$
-
1.
Betweenness (Definition 10) is an extension of the one-dimensional concept of Betweenness (Condition 3) of Definition 6 above. Betweenness (Definition 10) is a one-dimensional property that each induced weak order \(\precsim _i\) must satisfy.
Definition 11
(Restricted Solvability). A factorial proximity structure \((\mathscr {D},\precsim )\) satisfies Restricted Solvability iff, for any \(\mathfrak {d}_1,\mathfrak {d}_3,\mathfrak {d}_4,\mathfrak {d}_5,\mathfrak {d}_6\in \mathscr {D}\), if \((\mathfrak {d}_4,\mathfrak {d}_3)\precsim (\mathfrak {d}_5,\mathfrak {d}_6)\precsim (\mathfrak {d}_4,\mathfrak {d}_1)\), then there exists \(\mathfrak {d}_2\in \mathscr {D}\) such that \(\mathfrak {d}_1|\mathfrak {d}_2|\mathfrak {d}_3\) and \((\mathfrak {d}_4,\mathfrak {d}_2)\sim (\mathfrak {d}_5,\mathfrak {d}_6)\).
Just as the role of Solvability (Condition 5) of Definition 6 above is to determine a class of absolute difference structures of Definition 6 on the basis of which Fact 1 (Representation) above can be proved, so the role of Restricted Solvability is to determine a class of additive difference factorial proximity structures of Definition 15 below on the basis of which Theorem 1 (Representation) below can be proved.
Definition 12
(Archimedean Property). A factorial proximity structure \((\mathscr {D},\precsim )\) satisfies the Archimedean Property iff, for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\) with \(\mathfrak {d}_1\ne \mathfrak {d}_2\), any sequence \(\{\mathfrak {d}_5^{(i)}: \mathfrak {d}_5^{(i)}\in \mathscr {D},i=0,1,\ldots \}\) that varies on at most one factor, such that
is finite.
Just as the Archimedean Property (Condition 6) of Definition 6 above is a technically necessary condition to prove Fact 1 (Representation) above and Fact 5 (Representation) below, so the Archimedean Property (Definition 12) is a technically necessary condition to prove Fact 3 (Representation) below. Suppes et al. [7, p. 181] prove the following theorems:
Fact 3
(Representation). Suppose \((\mathscr {D},\precsim )\) is a factorial proximity structure that satisfies One-Factor Independence (Definition 9), Betweenness (Definition 10), Restrict Solvability (Definition 11), and the Archimedean Property (Definition 12). Then there exist real-valued functions \(f_i\) defined on \(\mathscr {D}_i\ (1\le i\le n)\) and real-valued function g that increases in each of n real arguments such that
and
Fact 4
(Uniqueness). The above functions \(f_i\) are interval scales, and the above function g is an ordinal scale.
2.2.2.4 Fourth Step
In order to represent the sum of dimensional factors, a factorial proximity structure \((\mathscr {D},\precsim )\) should satisfy Independence and the Thomsen Condition only for the dimensionality \(n=2\). Suppes et al. [7, p. 182] define these concepts as follows:
Definition 13
(Independence). A factorial proximity structure \((\mathscr {D},\precsim )\) satisfies Independence iff the following holds for any \(\mathfrak {d}_1,\mathfrak {d}_1',\mathfrak {d}_2,\mathfrak {d}_2',\mathfrak {d}_3,\mathfrak {d}_3',\mathfrak {d}_4,\mathfrak {d}_4'\in \mathscr {D}\): If the two elements in each of \((\mathfrak {d}_1,\mathfrak {d}_1'),(\mathfrak {d}_2,\mathfrak {d}_2'),(\mathfrak {d}_3,\mathfrak {d}_3'),(\mathfrak {d}_4,\mathfrak {d}_4')\) have identical components on one factor, and the two elements in each of \((\mathfrak {d}_1,\mathfrak {d}_3),(\mathfrak {d}_1',\mathfrak {d}_3'),(\mathfrak {d}_2,\mathfrak {d}_4),(\mathfrak {d}_2',\mathfrak {d}_4')\) have identical components on all the remaining factors, then
Remark 3
(One-Factor Independence and Independence) Independence (Definition 13) implies One-Factor Independence (Definition 9).
Just as One-Factor Independence (Definition 9) above is a necessary condition to prove Fact 3 (Representation) above, so Independence (Definition 13) is a necessary condition to prove Fact 5 (Representation) below.
Definition 14
(Thomsen Condition). A factorial proximity structure \((\mathscr {D},\precsim )\) with \(\mathscr {D}:=\mathscr {D}_1\times \mathscr {D}_2\) satisfies the Thomsen Condition iff, for any \(\mathfrak {d}_1^{(i)},\mathfrak {d}_2^{(i)},\mathfrak {d}_3^{(i)},\mathfrak {d}_4^{(i)},\mathfrak {d}_5^{(i)},\mathfrak {d}_6^{(i)}\in \mathscr {D}_i\ (i=1,2)\),
and
imply
Remark 4
(Thomsen Condition Only for Two Dimensionality). The Thomsen Condition must be assumed only when the dimensionality \(n=2\).
Suppes et al. [7, p. 183] prove the following theorems:
Fact 5
(Representation). Suppose that \((\mathscr {D},\precsim )\) is a factorial proximity structure that satisfies Restrict Solvability (Definition 11) and Independence (Definition 13), and that each structure \((\mathscr {D}_i,\precsim _i)\), where \(\precsim _i\) is an induced weak order on \(\mathscr {D}_i\times \mathscr {D}_i\), satisfies the Archimedean Property (Condition 6 of Definition 6). If \(n\ge 3\), then there exist real-valued functions \(f_i\) defined on \(\mathscr {D}_i\times \mathscr {D}_i\ (1\le i\le n)\) such that for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\),
iff
If \(n=2\), then the above assertions hold provided the Thomsen Condition (Definition 14) is also satisfied.
Fact 6
(Uniqueness). The above functions \(f_i\) are interval scales.
2.2.2.5 Fifth Step
The fifth step is a step to combine the third and fourth steps. Suppes et al. [7, p. 184] define an additive difference factorial proximity structure as follows:
Definition 15
(Additive Difference Factorial Proximity Structure). When \(n\ge 2\) and the factorial proximity structure \((\mathscr {D}(:=\displaystyle \prod _{i=1}^n \mathscr {D}_i), \precsim )\) satisfies Betweenness, Restricted Solvability, the Archimedean Property, Independence, and the Thomsen Condition, we call it an additive difference factorial proximity structure.
By combining Facts 3–6, Suppes et al. [7, p. 185] prove the following theorems:
Fact 7
(Representation). If \((\mathscr {D}, \precsim )\) is an additive difference factorial proximity structure (Definition 15), there exist real-valued functions \(f_i\) defined on \(\mathscr {D}_i\ (1\le i\le n)\) such that for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\),
iff
Fact 8
(Uniqueness). The above functions \(f_i\) are interval scales and the above functions \(g_i\) are interval scales with a common unit.
2.2.2.6 Sixth Step
The ontological status of an n-tuple \(\mathfrak {d}_1\cdots \mathfrak {d}_n\) in Definition 8 is not clear. So in order to describe the parthood between a particular and its parts referred to for determining the raking on a resemblance relation, we would like to introduce mereology:
Definition 16
(Mereology).
-
A mereological parthood relation P (Varzi [9, p.14]) is a binary relation on \(\mathscr {D}\) satisfying the following properties:
-
For any \(\mathfrak {d}\in \mathscr {D}\), \(P(\mathfrak {d},\mathfrak {d})\) (Reflexivity).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3\in \mathscr {D}\), if \(P(\mathfrak {d}_1,\mathfrak {d}_2)\) and \(P(\mathfrak {d}_2,\mathfrak {d}_3)\), then \(P(\mathfrak {d}_1,\mathfrak {d}_3)\) (Transitivity).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), if \(P(\mathfrak {d}_1,\mathfrak {d}_2)\) and \(P(\mathfrak {d}_2,\mathfrak {d}_1)\), then \(\mathfrak {d}_1\) equals \(\mathfrak {d}_2\) (Antisymmetry).
-
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), a mereological proper parthood relation \(PP(\mathfrak {d}_1,\mathfrak {d}_2)\) is such a binary relation on \(\mathscr {D}\) that \(P(\mathfrak {d}_1,\mathfrak {d}_2)\) and \(\mathfrak {d}_1\) does not equal \(\mathfrak {d}_2\).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), a mereological overlap relation \(O(\mathfrak {d}_1,\mathfrak {d}_2)\) is such a binary relation on \(\mathscr {D}\) that there exists \(\mathfrak {d}_3\in \mathscr {D}\) such that \(P(\mathfrak {d}_3,\mathfrak {d}_1)\) and \(P(\mathfrak {d}_3,\mathfrak {d}_2)\).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), if \(PP(\mathfrak {d}_1,\mathfrak {d}_2)\), then there exists \(\mathfrak {d}_3\in \mathscr {D}\) such that \(P(\mathfrak {d}_3,\mathfrak {d}_2)\) and not \(O(\mathfrak {d}_3,\mathfrak {d}_1)\) (Supplementation) (Varzi [9, pp.51-52]).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3\in \mathscr {D}\), a mereological product relation \(PR(\mathfrak {d}_3,\mathfrak {d}_1,\mathfrak {d}_2)\) is such a ternary relation on \(\mathscr {D}\) that \(P(\mathfrak {d}_4,\mathfrak {d}_3)\) iff \(P(\mathfrak {d}_4,\mathfrak {d}_1)\) and \(P(\mathfrak {d}_4,\mathfrak {d}_2)\), for any \(\mathfrak {d}_4\in \mathscr {D}\).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), then there exists \(\mathfrak {d}_3\in \mathscr {D}\) such that \(PR(\mathfrak {d}_3,\mathfrak {d}_1,\mathfrak {d}_2)\) (Product).
-
For any \(\mathfrak {d}_1,\mathfrak {d}_2\in \mathscr {D}\), we define \(\mathfrak {d}_1\bigotimes \mathfrak {d}_2\) as the uniquely existential object bearing the relation PR with \(\mathfrak {d}_1\) and \(\mathfrak {d}_2\), in symbols,
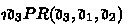 (Varzi [9, pp.51-52]).
(Varzi [9, pp.51-52]).
Example 2
(Rodriguez-Pereyra-Yi Problem and Mereology). In Rodriguez-Pereyra-Yi Problem, by means of a mereological parthood function P, we would like to describe the parthood between a particular and its parts referred to for determining the raking on resemblance relations with respect to carminity and vermillionity and triangularity. In this case, neither carminity, vermillionity nor triangularity themselves is reified.
2.2.2.7 Final Step
By connecting measurement-theoretic concepts with mereological concepts, we define a mereorogical additive difference factorial proximity structured model \(\mathfrak {M}\) of \(\textsf{RMRL}\):
Definition 17
(Mereorogical Additive Difference Factorial Proximity Structured Model).
-
The mereological additive difference factorial proximity structured frame of \(\textsf{RMRL}\) is a structure
$$ \mathfrak {F}:=(\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}), $$where
-
\(\mathscr {W}\) is a non-empty class of worlds,
-
R a binary accessibility relation on \(\mathscr {W}\),
-
\(\mathscr {D}\) a non-empty class of particulars,
-
\(\{\precsim _F\}_{F\in \mathscr {P}}\) a family of such quaternary relations \(\precsim _F\) on \(\mathscr {D}\) that \((\mathscr {D}, \precsim _F)\) is an absolute difference structure and \(\precsim _F\) satisfies Maximality of Definition 8,
-
\(\{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}\) a non-empty class of \(\mathscr {D}_{\precsim _F}\) which is a non-empty class of the parts of particulars referred to for determining the ranking on \(\precsim _F\) and which postulates that there exists a unique F-part of a particular belonging to \(\mathscr {D}\),
-
P a mereological parthood relation on \(\mathscr {D}\cup \displaystyle \bigcup _{F\in \mathscr {P}}\mathscr {D}_{\precsim _F}\) of Definition 16
-
\(\{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}\) a family of such quaternary relations \(\precsim _{F_1\times \cdots \times F_n}\) on \(\mathscr {D}_{F_1}\times \cdots \times \mathscr {D}_{F_n}\) that \((\mathscr {D}_{F_1}\times \cdots \times \mathscr {D}_{F_n}, \precsim _{F_1\times \cdots \times F_n})\) is an additive difference factorial proximity structure.
-
-
A function I is an interpretation of \(\mathfrak {F}\) if I
-
assigns to each \(a\in \mathscr {C}\) and each \(w\in \mathscr {W}\) some object that is a member of \(\mathscr {D}\) that satisfies Transworld Identity: for any \(w,w'\),
$$ I(a,w)=I(a,w'), $$and
-
assigns to each four-place resemblance predicate symbol \(\leqslant _F\) and each \(w\in \mathscr {W}\) such a quaternary relation \(\precsim _F\), and
-
assigns to each four-place resemblance predicate symbol \(\leqslant _{F_1\times \cdots \times F_n}\) and each \(w\in \mathscr {W}\) such a quaternary relation \(\precsim _{F_1\times \cdots \times F_n}^*\) that it is defined as follows:
if, for any particular \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\in \mathscr {D}\),
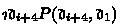 ,
,
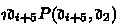 ,
,
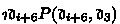 ,
,
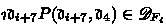 are such uniquely existential parts of \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\) respectively, then $$ (\mathfrak {d}_1,\mathfrak {d}_2)\precsim _{F_1\times \cdots \times F_n}^*(\mathfrak {d}_3,\mathfrak {d}_4) $$
are such uniquely existential parts of \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3,\mathfrak {d}_4\) respectively, then $$ (\mathfrak {d}_1,\mathfrak {d}_2)\precsim _{F_1\times \cdots \times F_n}^*(\mathfrak {d}_3,\mathfrak {d}_4) $$iff
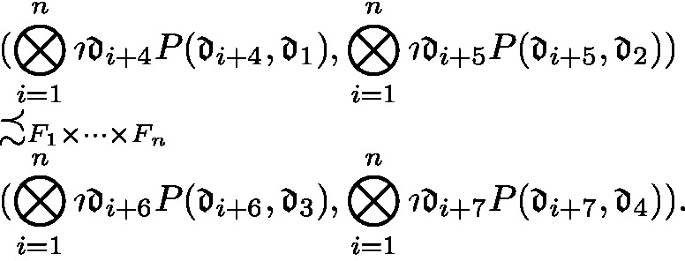
(Refer to Definition 16 for the definition of \(\otimes \).)
-
-
A property class I(F, w) is defined as a maximal resemblance class in terms of a resemblance relation \(\precsim _F\): \(A\subsetneq \mathscr {D}\) is a property class I(F, w) iff \((\mathscr {D}, \precsim _F)\) is an absolute difference structure and for any \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3\in A\) and for any \(\mathfrak {d}_4\in \overline{A}\),
$$ (\mathfrak {d}_1,\mathfrak {d}_2)\prec _F (\mathfrak {d}_3,\mathfrak {d}_4)\quad (Maximality ). $$ -
The mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\) is a structure
$$ \mathfrak {M}:=(\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}, I). $$
Remark 5
(\(\precsim _{F_1\times \cdots \times F_n}^*\) and \(\precsim _{F_1\times \cdots \times F_n}\)). In this definition, we consider the comparison (\(\precsim _{F_1\times \cdots \times F_n}^*\)) of differences of resemblance between particulars with respect to \(F_1\)-ness and \(\ldots \) and \(F_n\)-ness to be the comparison (\(\precsim _{F_1\times \cdots \times F_n}\)) of difference of resemblance between the n-tuple products of parts of a particular referred to for determining the raking on resemblance relations with respect to \(F_1\)-ness and \(\ldots \) and with respect to \(F_n\)-ness, respectively.
Remark 6
(Not Absoluteness But Conditionality). The mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\) does not require that \(\precsim _F\) should absolutely satisfy such conditions above as Betweenness and the Archimedean Property and so on, but requires that if \(\precsim _F\) satisfies them, then Theorems 1–4 below can be proven.
Remark 7
(Nominalism about Universals). \(\mathfrak {M}\) is nominalistic both about such universals as properties and about \(\precsim _F\) and R neither of which are reified, whereas it is Platonistic about such abstract objects as classes, functions, numbers and possible worlds. As Rodriguez-Pereyra [5] observes, Realism/Nominalism about universals is independent of Platonism/Nominalism about abstract objects.
Remark 8
(Non-Circularity of Resemblance Relation). Since a resemblance relation \(\precsim _F\) depends not on a property class I(F, w) defined by \(\precsim _F\) but on a predicate symbol F, where I(F, w) is the semantic value of F. In this sense, \(\precsim _F\) is not circular.
Remark 9
(Reducibility and Resemblance Nominalism). \(\mathfrak {M}\) is resemblance-nominalistic in the sense that I(F, w) is reducible to \(\precsim _F\).
2.2.3 Satisfaction Definition
We define an (extended) assignment as follows:
Definition 18
((Extended) Assignment).
-
We call \(s: \mathscr {V}\rightarrow \mathscr {D}\) an assignment.
-
\(\tilde{s}: \mathscr {V}\cup \mathscr {C}\rightarrow \mathscr {D}\) is defined as follows:
-
1.
For each \(x\in \mathscr {V}\), \(\tilde{s}(x)=s(x)\),
-
2.
For each \(a\in \mathscr {C}\) and each \(w\in \mathscr {W}\), \(\tilde{s}(a)=I(a,w)\).
We call \(\tilde{s}\) an extended assignment.
-
1.
We provide \(\textsf{MRL}\) with the following satisfaction definition relative to \(\mathfrak {M}\), define the truth (at a world) in \(\mathfrak {M}\) by means of satisfaction and then define validity as follows:
Definition 19
(Satisfaction).
-
What it means for \(\mathfrak {M}\) to satisfy \(\varphi \in \varPhi _{\mathcal {L}}\) at \(w\in \mathscr {W}\) with s, in symbols \((\mathfrak {M},w)\models \varphi [s]\) is inductively defined as follows:
-
\((\mathfrak {M},w)\models (t_1,t_2)\leqslant _F(t_3,t_4)[s]\) iff \((\tilde{s}(t_1),\tilde{s}(t_2))\precsim _F(\tilde{s}(t_3),\tilde{s}(t_4))\),
-
\((\mathfrak {M},w)\models (t_1,t_2)\leqslant _{F_1\times \cdots \times F_n}(t_3,t_4)[s]\) iff \((\tilde{s}(t_1),\tilde{s}(t_2))\precsim _{F_1\times \cdots \times F_n}^*(\tilde{s}(t_3),\tilde{s}(t_4))\),
-
\((\mathfrak {M},w)\models F(t)[s]\) iff \(\tilde{s}(t)\in I(F,w)\), where I(F,w) is defined by Definition 17,
-
\((\mathfrak {M},w)\models t_1=t_2[s]\) iff \(\tilde{s}(t_1)=\tilde{s}(t_2)\),
-
\((\mathfrak {M},w)\models \top [s]\),
-
\((\mathfrak {M},w)\models \lnot \varphi [s]\) iff \((\mathfrak {M},w)\not \models \varphi [s]\),
-
\((\mathfrak {M},w)\models \varphi \wedge \psi [s]\) iff \((\mathfrak {M},w)\models \varphi [s]\) and \((\mathfrak {M},w)\models \psi [s]\),
-
\((\mathfrak {M},w)\models \Box \varphi [s]\) iff for all \(w\in \mathscr {W}\) such that \(R(w,w')\), \((\mathfrak {M},w')\models \varphi [s]\),
-
\((\mathfrak {M},w)\models \forall x\varphi [s]\) iff for any \(\mathfrak {d}\in \mathscr {D}\), \(\mathfrak {M}\models \varphi [s(x|\mathfrak {d})]\), where \(s(x|\mathfrak {d})\) is the function that is exactly like s except for one thing: for the individual variable x, it assigns the object \(\mathfrak {d}\). This can be expressed as follows:
$$ s(x|d)(y)\ :=\ {\left\{ \begin{array}{ll} s(y) &{} \text{ if }\quad y\ne x\\ \mathfrak {d} &{} \text{ if }\quad y=x. \end{array}\right. } $$
-
-
If \((\mathfrak {M},w)\models \varphi [s]\) for all s, we write \((\mathfrak {M},w)\models \varphi \) and say that \(\varphi \) is true at w in \(\mathfrak {M}\).
-
If \((\mathfrak {M},w)\models \varphi \) for all \(w\in \mathscr {W}\), we write \(\mathfrak {M}\models \varphi \) and say that \(\varphi \) is true in \(\mathfrak {M}\).
-
If \(\varphi \) is true in any model based on the frame of \(\textsf{MRL}\), we write \(\models \varphi \) and say that \(\varphi \) is valid.
The next corollary follows from Definitions 17 and 19:
Corollary 1
(Property Class and Resemblance Relation).
iff
iff for any \(\mathfrak {d}_2,\mathfrak {d}_3\in I(F,w)\) and for any \(\mathfrak {d}_3\in \overline{I(F,w)}\),
Remark 10
(Definability by Resemblance Relation). The satisfaction clause of F(t) can be defined by a resemblance relation \(\prec _F\).
2.2.4 Representation and Uniqueness Theorems
Then the next theorems follows from Facts 1 and 2 and Definition 19.
Theorem 1
(Representation). If \((\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}, I)\) is a mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\), then there exists a function \(f:\mathscr {D}\rightarrow \mathbb {R}\) satisfying
iff
iff
Proof
Suppose that \((\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}, I)\) is a mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\) (Definition 17). Then because, by Definition 17, \((\mathscr {D}, \precsim _F)\) is an absolute difference structure (Definition 6), by Fact 1, there exists a function \(f:\mathscr {D}\rightarrow \mathbb {R}\) satisfying
iff
On the other hand, by Definition 19, we have
iff
Theorem 2
(Uniqueness). The above function f is a quasi-interval scale.
By Facts 7 and 8 and Definition 19, we can prove the following representation and uniqueness theorems for \(\precsim _{F_1\times \cdots \times F_n}\):
Theorem 3
(Representation). If \((\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}, I)\) is a mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\), then there exist functions \(f_{\precsim _{F_i}} (1\le i\le n): \mathscr {D}_{\precsim _{F_i}}\rightarrow \mathbb {R}_{\ge 0}\) and monotonically increasing functions \(g_{\precsim _{F_i}} (1\le i\le n): \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}_{\ge 0}\) such that
iff
iff

where
 ,
,
 .
.
Proof
Suppose that \((\mathscr {W}, R, \mathscr {D}, \{\precsim _F\}_{F\in \mathscr {P}}, \{\mathscr {D}_{\precsim _F}\}_{F\in \mathscr {P}}, P, \{\precsim _{F_1\times \cdots \times F_n}\}_{F_1\ldots ,F_n\in \mathscr {P}}, I)\) is a mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\) (Definition 17). Then because, by Definition 17, \((\mathscr {D}_{F_1}\times \cdots \times \mathscr {D}_{F_n}, \precsim _{F_1\times \cdots \times F_n})\) is an additive difference factorial proximity structure (Definition 15), by Fact 7, there exist functions \(f_{\precsim _{F_i}} (1\le i\le n): \mathscr {D}_{\precsim _{F_i}}\rightarrow \mathbb {R}_{\ge 0}\) and monotonically increasing functions \(g_{\precsim _{F_i}} (1\le i\le n): \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}_{\ge 0}\) such that
iff

On the other hand, by Definition 19, we have
iff
Remark 11
(Mereological Parthood Relation). One of the points of this theorem is that it is formulated by the help of a mereological parthood relation P.
Theorem 4
(Uniqueness). The above functions \(f_{\precsim _{F_i}}\) are interval scales and the above functions \(g_{\precsim _{F_i}}\) are interval scales with a common unit.
We define the degree of unresemblance and its weight in terms of Theorems 3 and 4:
Definition 20
(Degree of Unresemblance and Its Weight). The degrees of unresemblance with respect to \(\precsim _{F_i}\) are defined by

and

of (4), and their weights are defined by
of (4), where the existence and uniqueness of \(f_{\precsim _{F_i}}\) and \(g_{\precsim _{F_i}}\) are guaranteed by Theorems 3 and 4 respectively.
3 Concluding Remarks
Suppose that
\(Cx:=\) x is carmine,
\(Vx:=\) x is vermillion,
\(Tx:=\) x is triangular, and
\((x,y)<_{C\times V\times T}(z,w):=\) x resembles y more than z resembles w with respect to carminity and vermillionity and triangularity. Then the \(\textsf{RMRL}\)-logical form of (1) is
Its semantic value (satisfaction condition) is given by the following corollary that follows from Theorem 3 and Definition 19:
Corollary 2
(Solution to Rodriguez-Pereyra-Yi Problem by \(\textsf{RMRL}\)). If \((\mathscr {W}, R, \mathscr {D}, \{\precsim _C,\precsim _V,\precsim _T\}, \{\mathscr {D}_{\precsim _C},\mathscr {D}_{\precsim _V},\mathscr {D}_{\precsim _T}\}, P, \{\precsim _{C\times V\times T}\}, I)\) is a mereological additive difference factorial proximity structured model of \(\textsf{RMRL}\), then there exist \(f_{\precsim _C}: \mathscr {D}_{\precsim _C}\rightarrow \mathbb {R}_{\ge 0}\) and \(f_{\precsim _V}: \mathscr {D}_{\precsim _V}\rightarrow \mathbb {R}_{\ge 0}\) and \(f_{\precsim _T}: \mathscr {D}_{\precsim _T}\rightarrow \mathbb {R}_{\ge 0}\) and \(g_{\precsim _C},g_{\precsim _V},g_{\precsim _T}: \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}_{\ge 0}\) such that
iff there is no \(\mathfrak {d}_1,\mathfrak {d}_2,\mathfrak {d}_3\in \mathscr {D}\) such that \(\mathfrak {d}_1\in I(C,w)\) and \(\mathfrak {d}_2\in I(V,w)\) and \(\mathfrak {d}_3\in I(T,w)\) such that

We have the following conclusion: When we choose as the weight-assignment functions such functions \(g_{\precsim _C},g_{\precsim _V},g_{\precsim _T}\) that the value of \(g_{\precsim _T}\) is much greater than those of \(g_{\precsim _C}\) and \(g_{\precsim _V}\), Corollary 2 can give a solution to Rodriguez-Pereyra-Yi Problem by Definition 20 in terms of giving the satisfaction condition of (1) in \(\textsf{RMRL}\) so that
the weighted sum of the degrees of unresemblance of carmine particulars to triangular particulars may be greater than that of carmine particulars to vermillion particulars,
instead of using Definition 1 that is the main culprit of this problem. In so doing, \(\textsf{RMRL}\) obtains the capacity to deal with multidimensionality in general beyond Rodriguez-Pereyra-Yi Problem.
References
Krantz, D.H., et al.: Foundations of Measurement, vol. 1. Academic Press, New York (1971)
Lewis, D.: On the Plurality of Worlds. Basil Blackwell, Oxford (1986)
Roberts, F.S.: Measurement Theory. Addison-Wesley, Reading (1979)
Rodriguez-Pereyra, G.: Resemblance Nominalism. Clarendon Press, Oxford (2002)
Rodriguez-Pereyra, G.: Nominalism in metaphysics. Stanford Encyclopedia of Philosophy (2015)
Rodriguez-Pereyra, G.: Resemblance nominalism and abstract nouns. Analysis 75, 223–231 (2015)
Suppes, P., et al.: Foundations of Measurement, vol. 2. Academic Press, San Diego (1989)
Suzuki, S.: Measurement-theoretic foundations of resemblance nominalism. In: Mineshima, K. (ed.) Proceedings of the Seventeenth Workshop on Logic and Engineering of Natural Language Semantics (LENLS17). JSAI, Tokyo (2020)
Varzi, A.: Mereology. Stanford Encyclopedia of Philosophy (2019)
Yi, B.U.: Abstract nouns and resemblance nominalism. Analysis 74, 622–629 (2014)
Yi, B.U.: Nominalism and comparative similarity. Erkenntnis 83, 793–803 (2018)
Acknowledgements
The author would like to thank the reviewers and the audience of LENLS19 for their very helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Suzuki, S. (2023). Measurement Theory Meets Mereology in Multidimensionality in Resemblance Nominalism. In: Bekki, D., Mineshima, K., McCready, E. (eds) Logic and Engineering of Natural Language Semantics. LENLS 2022. Lecture Notes in Computer Science, vol 14213. Springer, Cham. https://doi.org/10.1007/978-3-031-43977-3_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-43977-3_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43976-6
Online ISBN: 978-3-031-43977-3
eBook Packages: Computer ScienceComputer Science (R0)





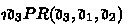 (Varzi [
(Varzi [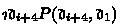 ,
,
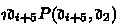 ,
,
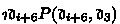 ,
,
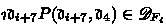 are such uniquely existential parts of
are such uniquely existential parts of