Study of MHD with Couple Stress Fluid on Squeeze-Film Characteristics of Curved Annular Circular Plates

Abstract

The consequences of couple stress fluid and applied magnetic field on the squeeze-film attributes between the curved annular circular plates are analyzed. Solving the governing equations, the non-dimensional expressions for film pressure, load-carrying capacity, and squeezing time are obtained, and results are discussed by plotting graphically for various parameters like Hartmann number, couple stress parameter, and curvature parameter. It is observed that the transverse magnetic field and couple stress fluid increase the load capacity, time of squeeze film and pressure. Also, it was noted that an increase in upper plate curvature increases the pressure, whereas increases in lower plate curvature decrease the loading-capacity and time of squeeze film.

1 Introduction

Magnetohydrodynamics is defined by the movement of electrically conducting fluids when electric and magnetic fields exist. For some decades, in the area of lubrication related to hydrodynamics, the characteristics of couple stress fluid (CSF) for various bearings have been studied by assuming that the lubricant has constant viscosity, though it is dependent on both temperature and pressure. In the past few years, Stokes micro continuum model [1] is the most fundamental one, and it allows polar effects for both, couple stress and body couples.

Researchers in the field of tribology are more interested in the usage of some additives as lubricants when a magnetic field is applied. Current research experiments [2, 3] based on oil combined with long-chain additives have shown that they enhance lubrication by reducing friction and surface damage. A modified form of the Reynolds equation was solved using a finite difference method by Elsharkawy [4], who attempted to examine the effects of geometry, pressure distribution, load carrying capacity, side leakage flow, and friction factor. The results showed that additives increase load carrying capacity while decreasing friction and side leakage coefficients. The authors formulated the modified Reynolds equation and found that lubricants with additives efficiently increase load supporting capacity and decrease the friction coefficient in comparison to Newtonian fluids. Naduvinamani et al. [5] and Ramesh Kudenatti et al. [6] detected that the impact of magnetohydrodynamics is essential for improving the time of squeezing film and load carrying. Syeda et al. [7] analyzed the squeeze-film character on various finite plates and noticed the enhanced performance of bearings in the presence of couple stress and MHD. Hanumagowda et al. [8] found that in conical bearings the magnetic field along with CSF enhances the properties of squeeze film. The study of the squeezing behavior of couple stress, between a flat plate and a sphere is analyzed by Lin [9], and it is noticed that the squeezing features of the system are enhanced. Naduvinamani and Siddangouda [10] analyzed theoretically that the couple stress variable impacts the performance of the squeeze film linking the circular stepped plates. It was observed that the CSF increases load support capacity and pressure and then decreases the squeezing time compared to the Newtonian fluids. Naduvinamani et al. [11] investigate the rheological effects of CSF on the squeezing behavior of porous journal bearings and indicate an increase in loading capacity. The combined impact of MHD and couple stress in anisotropic plates has been studied by Fathima et al. [12]. They found that the modified Reyonld’s equation obtained with the combination of MHD and CSF is very beneficial for industrial applications. Hanumagowda et al. [13] examined the impact of CSF and magnetohydrodynamics on the characteristics of curved circular plates between squeeze film. With these results, it can be observed that there is an improvement in squeeze film. In this chapter, the consequences of magnetohydrodynamics and CFS on squeeze-film behavior between the curved annular circular plates are examined.

1.1 Theoretical Solution

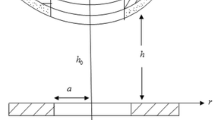
Figure 1 shows the lubrication of squeeze film between two curved annular circular plates in the presence of a transverse magnetic field. The two curved annular circular plates are separated by a fluid film of central thickness h_m, and ‘a’ and ‘b’ are the inner and outer radii of the circle of the annular plate, respectively. A magnetic field B₀ is enforced perpendicular to the plates. β and γ are the curvature parameters for the upper and lower plates, respectively.

Fig. 1

Geometrical arrangement of curved annular circular plates

The thickness of fluid film is given as h( r)

$$ h\left(\;r\right)={h}_m\left\{\exp \left(-\beta .{r}^2\right)-\frac{1}{1+\gamma\;r}+1\right\};\kern0.5em a\le r\le b $$

(1)

The derived modified Reynolds equation by Hanumagowda et al. [13] for MHD couple-stress squeeze film between curved circular plates is

$$ \frac{1}{r\mu}.\frac{\partial }{\partial r}\left[\;r.S\left(h,l,{M}_0\right)\;\frac{\partial p}{\partial r}\right]=V $$

(2)

Where,

$$ S\left(h,l,{M}_0\right)=\left\{\begin{array}{ll}\frac{h_m^2}{M_0^2}\left\{\frac{2l}{\left({A}^2-{B}^2\right)}\left(\frac{B^2}{A}\tanh\;\frac{A.h}{2l}-\frac{A^2}{B}\tanh \frac{Bh}{2l}\right)+h\right\},& \textrm{for}\kern0.48em {M}_0^2{l}^2/{h}_m^2<1\\ {}\frac{h_m^2}{M_0^2}\left\{\frac{h}{2}\sec {h}^2\left(\frac{h}{2\sqrt{2l}}\right)-3\sqrt{2l}\tanh \left(\frac{h}{2\sqrt{2l}}\right)+h\right\},& \textrm{for}\kern0.24em {M}_0^2{l}^2/{h}_m^2=1\\ {}\frac{h_m^2}{M_0^2}\left\{\frac{2{lh}_0}{M}\left(\frac{\left({A}_2\cot \theta -{B}_2\right)\sin {B}_2h-\left({B}_2\cot \theta +{A}_2\right)\sin {A}_2h}{\cos {B}_2h+\cosh {A}_2h}\right)+h\right\},& \textrm{for}\kern0.24em {M}_0^2{l}^2/{h}_m^2>1\end{array}\right. $$

The non-dimensional quantities given below are used in (2)

$$ {r}^{\ast }=\frac{r}{a},\kern0.3em {h}^{\ast }=\frac{h}{h_{m0}},{h}_m^{\ast }=\frac{h_m}{h_{m0}},{l}^{\ast }=\frac{2l}{h_{m0}},\kern0.3em C=\beta {a}^2,K=\gamma a,P=-\frac{h_{m0}^3p}{\mu {a}^2V} $$

The Reynolds equation in the modified form is

$$ \frac{1}{r^{\ast }}\frac{\partial }{\partial {r}^{\ast }}\left\{{r}^{\ast }F\left({h}^{\ast },{l}^{\ast },{M}_0\right)\frac{\partial P}{\partial {r}^{\ast }}\right\}=-1 $$

(3)

Where,

$$ F\left({h}^{\ast },{l}^{\ast },{M}_0\right)=\left\{\begin{array}{ll}\frac{1}{M_0^2}\left\{\frac{l^{\ast }}{\left({A}^{\ast 2}-{B}^{\ast 2}\;\right)}\left(\frac{B^{\ast 2}}{A^{\ast }}\tanh \frac{A^{\ast }{h}^{\ast }}{l^{\ast }}-\frac{A^{\ast 2}}{B^{\ast }}\tan\;\textrm{h}\frac{B^{\ast }{h}^{\ast }}{l^{\ast }}\right)+{h}^{\ast}\right\}& \textrm{for}\kern0.6em 4{M}_0^2{l}^{\ast 2}<1\\ {}\frac{1}{M_0^2}\left\{\frac{h^{\ast }}{2}{Sech}^2\left(\frac{h^{\ast }}{\sqrt{2}{l}^{\ast }}\right)-\frac{3{l}^{\ast}\kern0.1em }{\sqrt{2}}\kern0.2em \mathit{\tanh}\left(\frac{h^{\ast }}{\sqrt{2}{l}^{\ast }}\right)+{h}^{\ast}\right\}& \textrm{for}\kern0.5em 4{M}_0^2{l}^{\ast 2}=1\\ {}\frac{1}{M_0^2}\left\{\frac{l^{\ast}\left({A}_2^{\ast } Cot{\theta}^{\ast }-{B}_2^{\ast}\right){SinB}_2^{\ast }{h}^{\ast }-{l}^{\ast}\left({B}_2^{\ast } Cot{\theta}^{\ast }+{A}_2^{\ast}\right){SinhA}_2^{\ast }{h}^{\ast }}{M_0\left({CosB}_2^{\ast }{h}^{\ast }+{CoshA}_2^{\ast }{h}^{\ast}\right)}+{h}^{\ast}\kern0.1em \right\}& \textrm{for}\kern0.5em 4{M}_0^2{l}^{\ast 2}>1\end{array}\right. \vspace*{-7pt}$$

The boundary conditions for pressure is

$$ P=0\kern0.5em at\kern0.5em {r}^{\ast }={a}^{\ast }=a/b $$

(4(i))

$$ P=0\kern0.5em at\kern0.5em {r}^{\ast }=1 $$

(4(ii))

By solving Eq. (3) the association for film pressure P using the pressure boundary conditions (4(i)) and (4(ii)) is

$$ P=\frac{f_2\left({r}^{\ast}\right){f}_1(1)-{f}_1\left({r}^{\ast}\right){f}_2(1)}{2{f}_2(1)} $$

(5)

Where,

$$ {f}_1\left({r}^{\ast}\right)=\int_{r^{\ast }={a}^{\ast}}^{r^{\ast }}\frac{r^{\ast }}{F\left({h}^{\ast },{l}^{\ast },{M}_0\right)}{dr}^{\ast}\kern0.5em \textrm{and}\kern0.5em {f}_2\left({r}^{\ast}\right)=\int_{r^{\ast }={a}^{\ast}}^{r^{\ast }}\frac{1}{r^{\ast }F\left({h}^{\ast },{l}^{\ast },{M}_0\right)}{dr}^{\ast } $$

(6)

The equation for pressure is integrated over the film region to get the load supporting capacity

$$ W=\int_{r=a}^b2\pi rp\; dr $$

(7)

The load-carrying capacity W^∗ is given by

$$ {W}^{\ast }{=}\frac{Wh_{m0}^3}{2\pi \mu {b}^4\left(-{dh}_m/ dt\right)}{=}\frac{-1}{2}\int_{r^{\ast }{=}{a}^{\ast}}^1{f}_1\left({r}^{\ast}\right)\;{r}^{\ast}\;{dr}^{\ast }{+}\frac{1}{2}\frac{f_1(1)}{f_2(1)}\int_{r^{\ast }{=}{a}^{\ast}}^1{f}_2\left({r}^{\ast}\right)\;{r}^{\ast}\;{dr}^{\ast } $$

(8)

The squeeze-film time is

$$ {T}^{\ast }=\frac{Wh_{m0}^2}{\pi \mu {b}^4}t=\int_{h_m^{\ast}}^1\left(\frac{2{f}_2(1)}{f_2(1)\int_{r^{\ast }={a}^{\ast}}^1{f}_1\left({r}^{\ast}\right)\;{r}^{\ast}\;{dr}^{\ast }-{f}_1(1)\int_{r^{\ast }={a}^{\ast}}^1{f}_2\left({r}^{\ast}\right)\;{r}^{\ast}\kern0.24em {dr}^{\ast }}\right){dh}_m^{\ast } $$

(9)

2 Interpretation of Results

In this work, the characteristic behavior of squeeze-film lubrication in the presence of MHD and CSF on curved annular circular plates is analyzed. Numerical and graphical interpretation was carried out on parameters like Hartmann number M₀, couple stress parameters l*, β and γ. For a detailed analysis of the above quantities, we have chosen the following range: M₀ = 0, 2, 4, 6, 8, l^* = 0, 0.2, 0.4, 0.6, 0.8, β = 0.5, γ = 0.6, a^* = 0.2

2.1 Squeeze-Film Pressure

Figures 2 and 3 show the deviation of pressure P with r^* with distinct M₀ and l^* values with β = 0.5, γ = 0.6, and h _m^* = 1. It was noticed that pressure P increases with increasing M₀ and l^* values. The variation in P with r^* with varying values of β and γ is shown in Figs. 4 and 5. It is noted that pressure P is enhanced with higher β values, while P reduces with higher γ values.

Fig. 2

Non-dimensional pressure P variation with r^* for different values of M_o with t = 0.3, β = 0.5, γ = 0.6, α^* = 0.2, and ${h}_w^{\ast }$ = 1

Fig. 3

Non-dimensional pressure P variation with r^* for variation values of t^* with M₀ = 3, β = 0.5, γ = 0.6, α^* = 0.2, and ${h}_m^{\ast }$ = 1

Fig. 4

Non-dimensional pressure P variation with r^* for variation values of β with M₀ = 3, l^* = 0.3, γ = 0.6, a* = 0.2, and ${h}_m^{\ast }$ = 1

Fig. 5

Non-dimensional pressure P variation with r^* for variation values of γ with l^* = 0.3, β = 0.5, M₀ = 3, a^* = 0.2, and ${h}_w^{\ast }$ = 1

2.2 Load-Conducting Capacity

The deviation of load W^* with respect to β for varying M₀ and l^* values is shown in Figs. 6 and 7, respectively. It is understood that the impact of magnetohydrodynamics increases the load-conducting capacity than that of the non-magnetic field. Similarly, the couple stress parameter l^* also increases load than the Newtonian case. Figure 8 displays the change in load W^* with respect to β as a function of γ with M₀ = 3,a^* = 0.2,l^* = 0.3 and h_m^* = 1 and notes that the impact of γ is that it reduces load W^*. The graph of W^* with respect to β for distinct a^* values with M₀ = 3, γ =0.6, l^* = 0.3, and h_m^* = 1 is displayed in Fig. 9. It is found that for higher a^* = a/b values, the load W^* decreases.

Fig. 6

Non-dimensional load W^* variation with β for variation values of M₀ with l^* = 0.3, a^* = 0.2, γ = 0.6, and ${h}_w^{\ast }$ = 1

Fig. 7

Non-dimensional load W^* variation with β for variation values of l^* with M_o = 3, a^* = 0.2, γ = 0.6, and ${h}_w^{\ast }$ = 1

Fig. 8

Variation of non-dimensional load W^* with β for variation values of γ with M_o = 3, a^* = 0.2, l^* = 0.3, and ${h}_w^{\ast }$ = 1

Fig. 9

Non-dimensional load W^* varriation with β for variation values of a^* with M_s = 3, γ = 0.6, l^* = 0.3, and ${h}_w^{\ast }$ = 1

2.3 Squeeze-Film Time

The change in time T^* versus ${h}_m^{\ast }$ for various M₀ and l^* values is noted in Figs. 10 and 11, respectively. It was observed that the impact of Hartmann number and CSF increases the squeeze-film time in comparison to the non-magnetic and Newtonian case. Figure 12 displays the deviation T^* with respect to ${h}_m^{\ast }$ for the function of γ with M₀ = 3, a^* = 0.2, l^* = 0.3, and β = 0.5. We note that with higher γ values, the squeezing time decreases. The profile of T^* with respect to ${h}_m^{\ast }$ for definite a^* values with M₀ = 3, γ = 0.6, l^* = 0.3 and β = 0.5 is shown in Fig. 13. It is found that T^* reduces as a^* = a/b increases.

Fig. 10

Non-dimensional squeezing T^* variation with ${h}_m^{\ast }$ for variation values of M_o with l^* = 0.3, a^* = 0.2, γ = 0.6, and β = 0.5

Fig. 11

Non-dimensional squeezing T^* variation with ${h}_m^{\ast }$ for variation values of t^* with M_o = 3, a^* = 0.2, γ = 0.6, and β = 0.5

Fig. 12

Non-dimensional squeezing T^* variation with ${h}_m^{\ast }$ for variation values of γ with M_o = 3, a^* = 0.2, l^* = 0.3, and β = 0.5

Fig. 13

Non-dimensional squeezing T^* variation with ${h}_j^{\ast }$ for variation values of a^* with M_o = 3, γ = 0.6, l^* = 0.3, and β = 0.5

3 Conclusion

In this research chapter, we have studied the collective impact of CSF and the applied magnetic field among curved annular round plates and drawn the following conclusions:

• (i) Due to the impact of the magnetic field, the squeeze-film lubrication performance improves in comparison to the non-magnetic case.

• (ii) The parameters pressure, squeezing time, and load-capacity increase with respect to the couple stress parameter when compared to the Newtonian fluid.

• (iii) Pressure P increases as the curvature parameter for the upper plate, that is β, increases.

• (iv) The load, squeeze time, and pressure reduce as the curvature parameter for the lower plate, that is γ, increases; this implies that the curvature parameter for the lower plate must be kept minimal for better results.

• (v) As the ratio between the inner and outer radii of the circle of annular plates, that is a^*, increases, the load and squeezing time reduce.

This work can be extended by studying the impact of MHD along with CFS and surface roughness on the squeezing behavior of curved annular circular plates.