Combined Effects of Magnetic Field and Heat Source on Double-Diffusive Marangoni Convection in Fluid-Porous Structure

Abstract

The problem of double-diffusive Marangoni convection (DDMC) in a fluid-porous structure, which is horizontally infinite, is investigated in the presence of constant heat source/sink in both the layers as well as a uniform vertical magnetic field. This composite layer is enclosed by adiabatic and isothermal boundaries. The system of ordinary differential equations is solved in closed form for the thermal Marangoni number (tMn), which is an eigenvalue, for adiabatic-adiabatic and adiabatic-isothermal boundary combinations. In-depth comparisons between the various parameters and depth ratio are made. It is noted that the thermal Marangoni number for the adiabatic-adiabatic thermal boundary condition is higher than that for the adiabatic-isothermal boundary condition as examined in detail. As a result, the fluid-porous structure is stable and can be employed in situations where convection needs to be controlled in the case of an adiabatic-adiabatic thermal boundary condition.

1 Introduction

In a variety of conditions, double-diffusive natural convection, or flows caused by buoyancy due to simultaneous temperature and concentration gradients, can occur. Some literature is available on the single and double component layer. Sumithra and Manjunatha [1] conducted an analytical study of magneto convection in a combined layer limited by adiabatic boundaries. Sankar et al. [2] and Jagadeesha et al. [3] examined the two-component convection using the Darcy model for porous enclosure in the presence of heat and solute source. Pushpa et al. [4] explored the thermosolutal convection. The influence of magnetic field on double-diffusive mixed convection in a rectangular inclined domain with an aspect ratio was investigated using a finite volume technique by Shivananda and Satheesh [5]. Shivakumara et al. [6] explored the effect of cross-diffusion on the beginning of convective instability. Sumithra and Arul Selvamary [7] discussed the single component convection for couple stress fluid in combined system for two boundary combinations. In the presence of magnetic field, heat generation or absorption, and chemical reaction, Xiaoli Qiang et al. [8] investigated unstable MHD double-diffusive convection flows between two infinite vertical parallel plates. Peristaltically deformable and double-diffusive characteristics have been examined by Tanveer et al. [9].

Recently, the influence of a power law fluid and an angled magnetic field on a porous material in a staggered cavity is studied by Hussain et al. [10]. The influence of the Soret and Dufour factors is also considered. Meften [11] investigated two models of double-diffusive convection in a fluid layer where viscosity varies quadratically with temperature and nonlinear results are obtained using conditional energy analysis. Manjunatha et al. [12] and Manjunatha and Sumithra [13] studied the effects of three profiles and a heat source on convection in a combined structure in the presence of magnetic field. In the present study, the effect of magnetic field and heat source on onset convection is examined in detail for two types of boundary combinations.

2 Mathematical Formulation

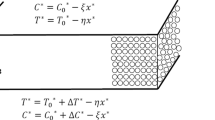
Consider a double component, electrically conducting liquid saturated isotropic, sparsely packed porous layer of thickness ${{d}_{p}}$ with an imposed magnetic field intensity ${{H}_{0}}$ underlying a triple component liquid layer of thickness ${{d}_{f}}$ and with heat sources ${{\varPhi }_{p}}$ and ${{\varPhi }_{f}}$, respectively. The porous layer’s lower surface is hard, while the fluid layer’s upper surface is free, with surface tension effects depending on temperature and concentration as shown in Fig. 1. A Cartesian coordinate system (x, y, z) is used with the origin at the interface between the porous and fluid layers, and the z-axis is vertically upward. Let $\varDelta T$ and $\varDelta C$ be the temperature and concentration difference between the lower and upper boundaries, $T={{T}_{0}}$ the reference temperature, and $C={{C}_{0}}$ the reference salinity. With the Boussinesq approximation, the basic equations for region 1 and region 2 (see Sumithra and Manjunatha [1] and Shivakumara et al. [14]).

Fig. 1

Geometry of the problem

Fluid layer: Region 1

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\nabla }_{f}}.{{\overrightarrow {V}}_{f}}=0 \end{array} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla_{f}.\overrightarrow{H}=0 \end{array} \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial {{{\overrightarrow {V}}}_{f}}}{\partial t}+({{\overrightarrow {V}}_{f}}.{{\nabla }_{f}}){{\overrightarrow{V}}_{f}}=-\frac{1}{{{\rho }_{0}}}{{\nabla }_{f}}{{P}_{f}}+\frac{{{\mu }_{f}}}{{{\rho }_{0}}}\nabla _{f}^{2}{{\overrightarrow {V}}_{f}}+\frac{{{\gamma }_{f}}}{{{\rho }_{0}}}(\overrightarrow{H}.{{\nabla }_{f}})\overrightarrow{H} \end{array} \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} \begin{array}{rcl}\frac{\partial {{T}_{f}}}{\partial t}+({{\overrightarrow{V}}_{f}}.{{\nabla }_{f}}){{T}_{f}}={{\kappa }_{f}}\nabla _{f}^{2}{{T}_{f}}+{{\varPhi }_{f}} \end{array} \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} \begin{array}{rcl}\frac{\partial {{C}_{f}}}{\partial t}+({{\overrightarrow{V}}_{f}}.{{\nabla }_{f}}){{C}_{f}}={{\kappa }_{cf}}\nabla _{f}^{2}{{C}_{f}} \end{array} \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} \begin{array}{rcl}\frac{\partial \overrightarrow{H}}{\partial t}={{\nabla }_{f}}\times {{\overrightarrow{V}}_{f}}\times \overrightarrow{H}+{{\nu }_{f}}\nabla _{f}^{2}\overrightarrow{H} \end{array} \end{aligned} $$

(6)

Porous layer: Region 2

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\nabla }_{p}}.\overrightarrow{V}_{p}=0 \end{array} \end{aligned} $$

(7)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\nabla }_{p}}.\overrightarrow{H}=0 \end{array} \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{1}{{{\varepsilon }_{p}}}\frac{\partial \overrightarrow{{{V}_{p}}}}{\partial t}+\frac{1}{\varepsilon _{p}^{2}}(\overrightarrow {{{V}_{p}}}.{{\nabla }_{p}})\overrightarrow {{{V}_{p}}}=-\frac{1}{{{\rho }_{0}}}{{\nabla }_{p}}{{P}_{p}}-\frac{{{\mu }_{p}}}{K{{\rho }_{0}}}\overrightarrow {{{V}_{p}}}+\frac{{{\gamma }_{p}}}{{{\rho }_{0}}}(\overrightarrow{H}.{{\nabla }_{p}})\overrightarrow{H} \end{array} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \begin{array}{rcl}M\frac{\partial {{T}_{p}}}{\partial t}+(\overrightarrow {{{V}_{p}}}.{{\nabla }_{p}}){{T}_{p}}={{\kappa }_{p}}\nabla _{p}^{2}{{T}_{p}}+{{\varPhi }_{p}} \end{array} \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\phi }_{p}}\frac{\partial {{C}_{p}}}{\partial t}+(\overrightarrow {{{V}_{p}}}.{{\nabla }_{p}}){{C}_{p}}={{\kappa }_{cp}}\nabla _{p}^{2}{{C}_{p}} \end{array} \end{aligned} $$

(11)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\phi }_{p}}\frac{\partial \overrightarrow{H}}{\partial t}={{\nabla }_{p}}\times \overrightarrow {{{V}_{p}}}\times \overrightarrow{H}+{{\nu }_{p}}\nabla _{p}^{2}\overrightarrow{H} \end{array} \end{aligned} $$

(12)

where the fluid and porous regions are denoted by the subscripts f and p, respectively. ${{\overrightarrow {V}}_{f}}$ is the velocity vector, ${{\rho }_{0}}$ is the fluid density, ${{\mu }_{f}}$ is the fluid viscosity, ${{P}_{f}}$ is the total pressure, $\overrightarrow {H}$ is the magnetic field, ${{T}_{f}}$ is the temperature, ${{\nu }_{f}}$ is the magnetic viscosity, ${{\gamma }_{f}}$ is the magnetic permeability, ${{\kappa }_{cf}}$ is the solute diffusivity of the fluid, and ${{C}_{f}}$ is the salinity field. For region 2, ${{\phi }_{p}}$ is the porosity, K is the permeability , M is the heat capacity ratio, ${{\kappa }_{p}}$ is the thermal diffusivity, and ${{\nu }_{p}}$ is the effective magnetic viscosity.

The goal of this research is to see if a quiescent state can withstand tiny perturbations superimposed on the basic state; the solutions are as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\overrightarrow{V}}_{f}}=0,{{P}_{f}}={{P}_{fb}}({{z}_{f}}),{{T}_{f}}={{T}_{fb}}({{z}_{f}}),{{C}_{f}}={{C}_{fb}}({{z}_{f}}),\overrightarrow{H}={{H}_{0}}({{z}_{f}}) \end{array} \end{aligned} $$

(13)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \overrightarrow {{{V}_{p}}}=0,{{P}_{p}}={{P}_{pb}}({{z}_{p}}),{{T}_{p}}={{T}_{pb}}({{z}_{p}}),{{C}_{p}}={{C}_{pb}}({{z}_{p}}),\overrightarrow{H}={{H}_{0}}({{z}_{p}}) \end{array} \end{aligned} $$

(14)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{T}_{fb}}({{z}_{f}})=\frac{-{{\varPhi }_{f}}{{z}_{f}}({{z}_{f}}-{{d}_{f}})}{2{{\kappa }_{f}}}+\frac{({{T}_{u}}-{{T}_{0}}){{z}_{f}}}{{{d}_{f}}}+{{T}_{0}}\quad \quad 0\le {{z}_{f}}\le {{d}_{f}} \\{{T}_{pb}}({{z}_{p}})=\frac{-{{\varPhi }_{p}}{{z}_{p}}({{z}_{p}}+{{d}_{p}})}{2{{\kappa }_{p}}}+\frac{({{T}_{0}}-{{T}_{l}}){{z}_{p}}}{{{d}_{p}}}+{{T}_{0}}\quad -{{d}_{p}}\le {{z}_{p}}\le 0 \\ {{C}_{fb}}({{z}_{f}})={{C}_{0}}-\frac{({{C}_{0}}-{{C}_{u}}){{z}_{f}}}{{{d}_{f}}}\quad \quad 0\le {{z}_{f}}\le {{d}_{f}}\\ {{C}_{pb}}({{z}_{p}})={{C}_{0}}-\frac{({{C}_{l}}-{{C}_{0}}){{z}_{p}}}{{{d}_{p}}}\quad \quad -{{d}_{p}}\le {{z}_{p}}\le 0 \end{array} \end{aligned} $$

$T_0=\frac {\kappa _{f}d_p T_u+\kappa _{p}d_f T_l}{\kappa _{f}d_p+\kappa _{p}d_f}+\frac {d_fd_p(\varPhi _{p}d_p+\varPhi _{f}d_f)}{2(\kappa _{f}d_p+\kappa _{p}d_f)}$, $C_o=\frac {{{\kappa }_{cf}}{{d}_{p}}{{C}_{u}}+{{\kappa }_{cp}}{{d}_{f}}{{C}_{l}}}{{{\kappa }_{cf}}{{d}_{p}}+{{\kappa }_{cp}}{{d}_{f}}}$.

To investigate the stability of the basic state, regions 1 and 2 are subjected to infinite perturbations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\overrightarrow{V}}_{f}}=\overrightarrow{V}_{f}^{\prime},{{P}_{f}}={{P}_{fb}}+P_{f}^{\prime},{{T}_{f}}={{T}_{fb}}({{z}_{f}})+\theta _{f}^{\prime},{{C}_{f}}={{C}_{fb}}({{z}_{f}})+S_{f}^{\prime},\\ \overrightarrow{H}={{H}_{0}}({{z}_{f}})+\overrightarrow{{H}^{\prime}} \end{array} \end{aligned} $$

(15)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \overrightarrow{{{V}_{p}}}={{\overrightarrow{{{V}_{p}}}}^{\prime }},{{P}_{p}}={{P}_{pb}}+P_{p}^{\prime},{{T}_{p}}={{T}_{pb}}({{z}_{p}})+\theta _{p}^{\prime},{{C}_{p}}={{C}_{pb}}({{z}_{p}})+S_{p}^{\prime},\\ \overrightarrow{H}={{H}_{0}}({{z}_{p}})+\overrightarrow{{H}^{\prime}} \end{array} \end{aligned} $$

(16)

where $\overrightarrow {V}_{f}^{\prime },P_{f}^{\prime },\theta _{f}^{\prime },S_{f}^{\prime },\overrightarrow {{H}^{\prime }}$velocity, pressure, temperature, salinity, and magnetic field are respectively perturbed quantities for region 1 and the similar quantities in region 2 are ${{\overrightarrow {{{V}_{p}}}}^{\prime }},P_{p}^{\prime },\theta _{p}^{\prime },S_{p}^{\prime },\overrightarrow {{H}^{\prime }}$. The variables are nondimensionalized for regions 1 and 2 using ${{d}_{f}}$, $\frac {d_{f}^{2}}{{{\kappa }_{f}}}$,$\frac {{{\kappa }_{f}}}{{{d}_{f}}}$,${{T}_{0}}-{{T}_{u}}$,${{C}_{0}}-{{C}_{u}}$,${{H}_{0}}$, and ${{d}_{p}},\frac {d_{p}^{2}}{{{\kappa }_{p}}},\frac {{{\kappa }_{p}}}{{{d}_{p}}}$,${{T}_{l}}-{{T}_{0}},{{C}_{l}}-{{C}_{0}}$, ${{H}_{0}}$.

We arrive at the following stability equations in region 1 and region 2, respectively, using the conventional linear stability analysis approach and assuming that the concept of exchange of stability holds (see Sumithra and Manjunatha [1] and Shivakumara et al. [14]):

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left( {{(D_{f}^{2}-a_{f}^{2})}^{2}}-{{Q}_{f}}D_{f}^{2} \right){{W}_{f}}({{z}_{f}})=0{} \end{array} \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} (D_{f}^{2}-a_{f}^{2}){{\theta }_{f}}({{z}_{f}})+\left( 1+R_{If}^{*}(2{{z}_{f}}-1) \right){{W}_{f}}({{z}_{f}})=0 {} \end{array} \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\tau}_{f}}(D_{f}^{2}-a_{f}^{2}){{S}_{f}}({{z}_{f}})+{{W}_{f}}({{z}_{f}})=0{} \end{array} \end{aligned} $$

(19)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left( (D_{p}^{2}-a_{p}^{2})+{{Q}_{p}}{{\beta }^{2}}D_{p}^{2} \right){{W}_{p}}({{z}_{p}})=0{} \end{array} \end{aligned} $$

(20)

$$\displaystyle \begin{aligned} \begin{array}{rcl} (D_{p}^{2}-a_{p}^{2}){{\theta }_{p}}({{z}_{p}})+\left( 1+R_{{I}p}^{*}(2{{z}_{p}}+1) \right){{W}_{p}}({{z}_{p}})=0{} \end{array} \end{aligned} $$

(21)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\tau }_{p}}(D_{p}^{2}-a_{p}^{2}){{S}_{p}}({{z}_{p}})+{{W}_{p}}({{z}_{p}})=0{} \end{array} \end{aligned} $$

(22)

In the above equations, ${{a}_{f}}$, ${{a}_{p}}$, ${{Q}_{f}}$, ${{Q}_{p}}$, $R_{If}^{*}=\frac {{{R}_{if}}}{2({{T}_{0}}-{{T}_{u}})}$, $R_{Ip}^{*}=\frac {{{R}_{ip}}}{2({{T}_{l}}-{{T}_{0}})}$, ${{R}_{if}}=\frac {{{\varPhi }_{f}}d_{f}^{2}}{{{\kappa }_{f}}}$, ${{R}_{ip}}=\frac {{{\varPhi }_{p}}d_{p}^{2}}{{{\kappa }_{p}}}$, ${{\tau }_{f}}=\frac {{{\kappa }_{cf}}}{{{\kappa }_{f}}}$, and ${{\tau }_{p}}=\frac {{{\kappa }_{cp}}}{{{\kappa }_{p}}}$ are, namely, the horizontal wave numbers, the Chandrasekhar numbers, the modified internal Rayleigh numbers, the internal Rayleigh numbers, and the diffusivity ratios, $\beta =\sqrt {\frac {K}{d_{p}^{2}}}$is the porous parameter, ${{W}_{f}}({{z}_{f}})$ and ${{W}_{p}}({{z}_{p}})$ are the vertical velocities, ${{\theta }_{f}}({{z}_{f}})$ and ${{\theta }_{p}}({{z}_{p}})$ are the temperatures, and ${{S}_{f}}({{z}_{f}})$ and ${{S}_{p}}({{z}_{p}})$ are the concentration distributions. Because the wave numbers for the combined layers must be the same, so that we have $\frac {{{a}_{f}}}{{{d}_{f}}}=\frac {{{a}_{p}}}{{{d}_{p}}}$ and hence ${{a}_{p}}=\hat {d}{{a}_{f}}$, here $\hat {d}=\frac {{{d}_{p}}}{{{d}_{f}}}$ is the depth ratio.

The boundary conditions are nondimensionalized after:

$$\displaystyle \begin{aligned} \begin{array}{rcl} D_{f}^{2}{{W}_{f}}(1)+\left( {{M}_{t}}{{\theta }_{f}}(1)+{{M}_{s}}{{S}_{f}}(1) \right)a_{f}^{2}=0{} \end{array} \end{aligned} $$

(23)

The velocity conditions are

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{W}_{f}}(1)=0,{{W}_{p}}(-1)=0,{{D}_{p}}{{W}_{p}}(-1)=0,\hat{T}{{W}_{f}}(0)={{W}_{p}}(0),\\ \hat{T}{{{\hat{d}}}^{2}}(D_{f}^{2}+a_{f}^{2}){{W}_{f}}(0)=\hat{\mu }(D_{p}^{2}+a_{p}^{2}){{W}_{p}}(0),\hat{T}\hat{d}{{D}_{f}}{{W}_{f}}(0)={{D}_{p}}{{W}_{p}}(0), \\ \hat{T}{{{\hat{d}}}^{3}}{{\beta }^{2}}[(D_{f}^{3}-3a_{f}^{2}{{D}_{f}})]{{W}_{f}}(0)=[-{{D}_{p}}+\hat{\mu }{{\beta }^{2}}(D_{p}^{3}-3a_{p}^{2}{{D}_{p}})]{{W}_{p}}(0){} \end{array} \end{aligned} $$

(24)

The conditions for adiabatic-adiabatic and adiabatic-isothermal, respectively, are

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{D}_{f}}{{\theta }_{f}}(1)=0,{{\theta }_{f}}(0)=\hat{T}{{\theta }_{p}}(0),{{D}_{f}}{{\theta }_{f}}(0)={{D}_{p}}{{\theta }_{p}}(0),{{D}_{p}}{{\theta }_{p}}(-1)=0{} \end{array} \end{aligned} $$

(25)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{D}_{f}}{{\theta }_{f}}(1)=0,{{\theta }_{f}}(0)=\hat{T}{{\theta }_{p}}(0),{{D}_{f}}{{\theta }_{f}}(0)={{D}_{p}}{{\theta }_{p}}(0),{{\theta }_{p}}(-1)=0 {} \end{array} \end{aligned} $$

(26)

The salinity conditions are

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{D}_{f}}{{S}_{f}}(1)=0,{{S}_{f}}(0)=\hat{S}{{S}_{p}}(0),{{D}_{f}}{{S}_{f}}(0)={{D}_{p}}{{S}_{p}}(0),{{D}_{p}}{{S}_{p}}(-1)=0 {} \end{array} \end{aligned} $$

(27)

In the above equations, $\hat {S}$ is the solute diffusivity ratio, $\hat {T}$ is the thermal ratio, $\hat {\mu }$ is the viscosity ratio, ${{M}_{t}}=\frac {\partial {{\sigma }_{t}}}{\partial {{T}_{f}}}\frac {({{T}_{u}}-{{T}_{0}}){{d}_{f}}}{{{\mu }_{f}}{{\kappa }_{f}}}$ is the thermal Marangoni number (tMn), ${{M}_{s}}=\frac {\partial {{\sigma }_{t}}}{\partial {{C}_{f}}}\frac {({{C}_{u}}-{{C}_{0}}){{d}_{f}}}{{{\mu }_{f}}{{\kappa }_{f}}}$is the solute Marangoni number (sMn), and ${{\sigma }_{t}}$ is the surface tension.

3 Methodology

Introducing (24), the velocity profiles are obtained by solving (17) and (20) and appropriately written as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{W}_{f}}({{z}_{f}}){=}{{A}_{1}}[\cosh {{\psi }_{f}}{{z}_{f}}{+}{{a}_{1}}\sinh {{\psi }_{f}}{{z}_{f}}{+}{{a}_{2}}\cosh {{\varphi }_{f}}{{z}_{f}}{+}{{a}_{3}}\sinh {{\varphi }_{f}}{{z}_{f}}] \end{array} \end{aligned} $$

(28)

$$\displaystyle \begin{aligned} \begin{array}{rcl}{{W}_{p}}({{z}_{p}}){=}{{A}_{1}}[{{a}_{4}}\cosh {{\delta }_{p}}{{z}_{p}}{+}{{a}_{5}}\sinh {{\delta }_{p}}{{z}_{p}}] \end{array} \end{aligned} $$

(29)

where

${{\psi }_{f}}=\frac {\sqrt {{{Q}_{f}}}+\sqrt {{{Q}_{f}}+4a_{f}^{2}}}{2},{{\varphi }_{f}}=\frac {\sqrt {{{Q}_{f}}}-\sqrt {{{Q}_{f}}+4a_{f}^{2}}}{2},$ ${{\delta }_{p}}=\sqrt {\frac {a_{p}^{2}}{1+{{Q}_{p}}{{\beta }^{2}}}},{{a}_{1}}=-\frac {{{a}_{3}}{{\varDelta }_{2}}}{{{\varDelta }_{1}}}$,

${{a}_{2}}=\frac {{{\varDelta }_{5}}{{\varDelta }_{7}}-{{\varDelta }_{8}}{{\varDelta }_{4}}}{{{\varDelta }_{3}}{{\varDelta }_{7}}-{{\varDelta }_{6}}{{\varDelta }_{4}}}$, ${{a}_{3}}=\frac {{{\varDelta }_{5}}{{\varDelta }_{6}}-{{\varDelta }_{8}}{{\varDelta }_{3}}}{{{\varDelta }_{4}}{{\varDelta }_{6}}-{{\varDelta }_{7}}{{\varDelta }_{3}}},{{a}_{4}}=\hat {T}(1+{{a}_{2}}),{{a}_{5}}=\frac {1}{{{\delta }_{p}}}(\hat {T}\hat {d}{{a}_{1}}{{\psi }_{f}}+{{a}_{3}}{{\varphi }_{f}})$

${{\varDelta }_{1}}=\widehat {{{d}^{2}}}{{\beta }^{2}}(\psi _{f}^{3}-3a_{f}^{2}{{\psi }_{f}})+{{\psi }_{f}},{{\varDelta }_{2}}=\widehat {{{d}^{2}}}{{\beta }^{2}}(\varphi _{f}^{3}-3a_{f}^{2}{{\varphi }_{f}})+{{\varphi }_{f}}$,

${{\varDelta }_{3}}=\hat {T}\cosh {{\delta }_{p}},{{\varDelta }_{4}}=-\frac {\hat {d}\hat {T}\sinh {{\delta }_{p}}}{{{\delta }_{p}}}({{\varphi }_{f}}-\frac {{{\varDelta }_{2}}{{\psi }_{f}}}{{{\varDelta }_{1}}})$,${{\varDelta }_{5}}=-{{\varDelta }_{3}},{{\varDelta }_{6}}=\cosh {{\varphi }_{f}}$,

${{\varDelta }_{7}}=\sinh {{\varphi }_{f}}-(\frac {{{\varDelta }_{2}}}{{{\varDelta }_{1}}})\sinh {{\psi }_{f}},{{\varDelta }_{8}}=-\cosh {{\psi }_{f}}$.

Introducing (19) and (22), the salinity profiles are obtained using the condition (27), as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{S}_{f}}({{z}_{f}})={{A}_{1}}[{{c}_{13}}\cosh {{a}_{f}}{{z}_{f}}+{{c}_{14}}\sinh {{a}_{f}}{{z}_{f}}+{{\varSigma }_{f1}}({{z}_{f}})] \end{array} \end{aligned} $$

(30)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{S}_{p}}({{z}_{p}})={{A}_{1}}[{{c}_{15}}\cosh {{a}_{p}}{{z}_{p}}+{{c}_{16}}\sinh {{a}_{p}}{{z}_{p}}+{{\varSigma }_{p1}}({{z}_{p}})] \end{array} \end{aligned} $$

(31)

where ${{\varSigma }_{f1}}({{z}_{f}})=\frac {-1}{{{\tau }_{f}}}\left [ \frac {\cosh {{\psi }_{f}}{{z}_{f}}+{{a}_{1}}\sinh {{\psi }_{f}}{{z}_{f}}}{\psi _{f}^{2}-a_{f}^{2}}+\frac {{{a}_{2}}\cosh {{\varphi }_{f}}{{z}_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}}{{z}_{f}}}{\varphi _{f}^{2}-a_{f}^{2}} \right ]$,

${{\varSigma }_{p1}}({{z}_{p}})=\frac {-1}{{{\tau }_{p}}}\left [ \frac {{{a}_{4}}\cosh {{\delta }_{p}}{{z}_{p}}+{{a}_{5}}\sinh {{\delta }_{p}}{{z}_{p}}}{\delta _{p}^{2}-a_{p}^{2}} \right ]$, ${{c}_{13}}=\hat {S}{{c}_{15}}+{{\varDelta }_{100}}+{{\varDelta }_{101}}$,

${{c}_{14}}=\frac {1}{{{a}_{f}}}({{c}_{16}}{{a}_{p}}+{{\varDelta }_{102}}+{{\varDelta }_{103}})$, ${{c}_{15}}=\frac {{{\varDelta }_{108}}{{a}_{p}}\cosh {{a}_{p}}-{{\varDelta }_{107}}{{\varDelta }_{105}}}{{{a}_{p}}\sinh {{a}_{p}}{{\varDelta }_{107}}+{{\varDelta }_{106}}{{a}_{p}}\cosh {{a}_{p}}}$,

${{c}_{16}}=\frac {{{\varDelta }_{105}}{{\varDelta }_{106}}+{{a}_{p}}\sinh {{a}_{p}}{{\varDelta }_{108}}}{{{a}_{p}}\sinh {{a}_{p}}{{\varDelta }_{107}}+{{\varDelta }_{106}}{{a}_{p}}\cosh {{a}_{p}}}$,${{\varDelta }_{100}}=\frac {-\hat {S}}{{{\tau }_{p}}}\left ( \frac {{{a}_{4}}}{\delta _{p}^{2}-a_{p}^{2}} \right )$,

${{\varDelta }_{101}}=\frac {1}{{{\tau }_{f}}}\left [ \frac {1}{\psi _{f}^{2}-a_{f}^{2}}+\frac {{{a}_{2}}}{\varphi _{f}^{2}-_{f}^{2}} \right ]$ ${{\varDelta }_{102}}=\frac {-1}{{{\tau }_{p}}}\left ( \frac {{{\delta }_{p}}{{a}_{5}}}{\delta _{p}^{2}-a_{p}^{2}} \right ),{{\varDelta }_{103}}=\frac {1}{{{\tau }_{f}}}(\frac {{{a}_{1}}{{\psi }_{f}}}{\psi _{f}^{2}-a_{f}^{2}}+\frac {{{a}_{3}}{{\varphi }_{f}}}{\varphi _{f}^{2}-_{f}^{2}})$

${{\varDelta }_{104}}=\frac {1}{{{\tau }_{f}}}\left [ \frac {(\sinh {{\psi }_{f}}+{{a}_{1}}\cosh {{\psi }_{f}}){{\psi }_{f}}}{\psi _{f}^{2}-a_{f}^{2}}+\frac {({{a}_{2}}\sinh {{\varphi }_{f}}+{{a}_{3}}\cosh {{\varphi }_{f}}){{\varphi }_{f}}}{\varphi _{f}^{2}-a_{f}^{2}} \right ]$,

${{\varDelta }_{105}}=\frac {1}{{{\tau }_{p}}}\left [ \frac {{{\delta }_{p}}(-{{a}_{4}}\sinh {{\delta }_{p}}+{{a}_{5}}\cosh {{\delta }_{p}})}{\delta _{p}^{2}-a_{p}^{2}} \right ]$,

${{\varDelta }_{106}}=\hat {S}{{a}_{f}}\sinh {{a}_{f}}\cosh {{a}_{p}}+{{a}_{p}}\sinh {{a}_{p}}\cosh {{a}_{f}}$,

${{\varDelta }_{107}}=\hat {S}{{a}_{f}}\sinh {{a}_{p}}\sinh {{a}_{f}}+{{a}_{p}}\cosh {{a}_{f}}\cosh {{a}_{p}}$,

${{\varDelta }_{108}}={{\varDelta }_{104}}-({{\varDelta }_{100}}+{{\varDelta }_{101}}){{a}_{f}}\sinh {{a}_{f}}-({{\varDelta }_{102}}+{{\varDelta }_{103}})\cosh {{a}_{f}}$.

4 Thermal Marangoni Number

4.1 Case (i): Adiabatic-Adiabatic Boundary Condition

The fluid-porous structure is horizontally enclosed by the adiabatic boundaries. Using the boundary conditions for temperature (25), the distributions ${{\theta }_{f}}({{z}_{f}})$ and ${{\theta }_{p}}({{z}_{p}})$ are produced by solving (18) and (21):

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\theta }_{f}}({{z}_{f}})={{A}_{1}}[{{c}_{1}}\cosh {{a}_{f}}{{z}_{f}}+{{c}_{2}}\sinh {{a}_{f}}{{z}_{f}}+{{\varSigma }_{f2}}({{z}_{f}})] \end{array} \end{aligned} $$

(32)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\theta }_{p}}({{z}_{p}})={{A}_{1}}[{{c}_{3}}\cosh {{a}_{p}}{{z}_{p}}+{{c}_{4}}\sinh {{a}_{p}}{{z}_{p}}+{{\varSigma }_{p2}}({{z}_{p}})] \end{array} \end{aligned} $$

(33)

where ${{\varSigma }_{f2}}({{z}_{f}})={{A}_{1}}[{{\delta }_{1}}-{{\delta }_{2}}+{{\delta }_{3}}-{{\delta }_{4}}],{{\varSigma }_{p2}}({{z}_{p}})={{A}_{1}}[{{\delta }_{5}}-{{\delta }_{6}}]$

${{\delta }_{1}}=\frac {({{\alpha }_{2f}}{{z}_{f}}+{{\alpha }_{1f}})}{(\psi _{f}^{2}-a_{f}^{2})}(\cosh {{\psi }_{f}}{{z}_{f}}+{{a}_{1}}\sinh {{\psi }_{f}}{{z}_{f}})$,

${{\delta }_{2}}=\frac {2{{\psi }_{f}}{{\alpha }_{2f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{1}}\cosh {{\psi }_{f}}{{z}_{f}}+\sinh {{\psi }_{f}}{{z}_{f}})$,

${{\delta }_{3}}=\frac {({{\alpha }_{2f}}{{z}_{f}}+{{\alpha }_{1f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{2}}\cosh {{\varphi }_{f}}{{z}_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}}{{z}_{f}})$,

${{\delta }_{4}}=\frac {2{{\varphi }_{f}}{{\alpha }_{2f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{3}}\cosh {{\varphi }_{f}}{{z}_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}}{{z}_{f}})$,

${{\delta }_{5}}=\frac {({{\alpha }_{1p}}+{{\alpha }_{2p}}{{z}_{p}})}{(\delta _{p}^{2}-a_{p}^{2})}({{a}_{4}}\cosh {{\delta }_{p}}{{z}_{p}}+{{a}_{5}}\sinh {{\delta }_{p}}{{z}_{p}})$,

${{\delta }_{6}}=\frac {2{{\alpha }_{2p}}{{\delta }_{p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}}({{a}_{5}}\cosh {{\delta }_{p}}{{z}_{p}}+{{a}_{4}}\sinh {{\delta }_{p}}{{z}_{p}})$,

${{\alpha }_{1f}}=R_{If}^{*}-1,{{\alpha }_{2f}}=-2R_{If}^{*},{{\alpha }_{1p}}=-(R_{Ip}^{*}+1),{{\alpha }_{2p}}=-2R_{Ip}^{*}$,

${{c}_{1}}={{c}_{3}}\hat {T}+{{\varDelta }_{10}}-{{\varDelta }_{11}}$, ${{c}_{2}}=\frac {1}{{{a}_{f}}}({{c}_{4}}{{a}_{p}}+{{\varDelta }_{12}}-{{\varDelta }_{13}})$, ${{c}_{3}}=\frac {{{\varDelta }_{19}}{{\varDelta }_{14}}-{{\varDelta }_{16}}{{\varDelta }_{18}}}{{{\varDelta }_{15}}{{\varDelta }_{18}}+{{\varDelta }_{17}}{{\varDelta }_{14}}}$,

${{c}_{4}}=\frac {{{\varDelta }_{16}}{{\varDelta }_{17}}+{{\varDelta }_{19}}{{\varDelta }_{15}}}{{{\varDelta }_{14}}{{\varDelta }_{17}}+{{\varDelta }_{18}}{{\varDelta }_{15}}}$,${{\varDelta }_{9}}=-[{{\delta }_{7}}+{{\delta }_{8}}+{{\delta }_{9}}+{{\delta }_{10}}]$,

${{\delta }_{7}}=\frac {{{\psi }_{f}}({{\alpha }_{2f}}+{{\alpha }_{1f}})}{(\psi _{f}^{2}-a_{f}^{2})}({{a}_{1}}\cosh {{\psi }_{f}}+\sinh {{\psi }_{f}})$,

${{\delta }_{8}}=\left [ \frac {{{\alpha }_{2f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2\psi _{f}^{2}{{\alpha }_{2f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}} \right ](\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}})$,

${{\delta }_{9}}=\frac {{{\varphi }_{f}}({{\alpha }_{2f}}+{{\alpha }_{1f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{3}}\cosh {{\varphi }_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}})$,

${{\delta }_{10}}=\left [ \frac {{{\alpha }_{2f}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2\varphi _{f}^{2}{{\alpha }_{2f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}} \right ]({{a}_{2}}\cosh \varphi +{{a}_{3}}\sinh \varphi )$,

${{\varDelta }_{10}}=\hat {T}\left [ \frac {{{\alpha }_{1p}}{{a}_{4}}}{(\delta _{p}^{2}-a_{p}^{2})}-\frac {2{{\alpha }_{2p}}{{\delta }_{p}}{{a}_{5}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}} \right ]$,

${{\varDelta }_{11}}=\frac {{{\alpha }_{1f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2{{\psi }_{f}}{{a}_{1}}{{\alpha }_{2f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}+\frac {{{a}_{2}}{{\alpha }_{1f}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2{{\varphi }_{f}}{{a}_{3}}{{\alpha }_{2f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}$,

${{\varDelta }_{12}}=\left [ \frac {{{\alpha }_{2p}}}{(\delta _{p}^{2}-a_{p}^{2})}-\frac {2\delta _{p}^{2}{{\alpha }_{2p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}} \right ]{{a}_{4}}+\frac {{{a}_{5}}{{\alpha }_{1p}}}{(\delta _{p}^{2}-a_{p}^{2})}$,

${{\varDelta }_{13}}=\frac {{{\alpha }_{1f}}{{\psi }_{f}}{{a}_{1}}+{{\alpha }_{2f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2{{\alpha }_{2f}}\psi _{f}^{2}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}+\frac {{{\alpha }_{1f}}{{\varphi }_{f}}{{a}_{3}}+{{\alpha }_{2f}}{{a}_{2}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2{{a}_{2}}{{\alpha }_{2f}}\varphi _{f}^{2}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}},$

${{\varDelta }_{14}}={{a}_{p}}\cosh {{a}_{p}},{{\varDelta }_{15}}={{a}_{p}}\sinh {{a}_{p}}$,

${{\varDelta }_{16}}=\left [ \frac {-{{\alpha }_{2p}}}{(\delta _{p}^{2}-a_{p}^{2})}+\frac {2\delta _{p}^{2}{{\alpha }_{2p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}} \right ]({{a}_{4}}\cosh {{\delta }_{p}}-{{a}_{5}}\sinh {{\delta }_{p}})-{{\varDelta }_{160}}$,

${{\varDelta }_{160}}=\frac {{{\delta }_{p}}({{\alpha }_{1p}}-{{\alpha }_{2p}})}{(\delta _{p}^{2}-a_{p}^{2})}({{a}_{5}}\cosh {{\delta }_{p}}-{{a}_{4}}\sinh {{\delta }_{p}})$, ${{\varDelta }_{17}}=\hat {T}{{a}_{f}}\sinh {{a}_{f}}$,

${{\varDelta }_{18}}={{a}_{p}}\cosh {{a}_{f}},{{\varDelta }_{19}}={{\varDelta }_{9}}-{{a}_{f}}({{\varDelta }_{10}}-{{\varDelta }_{11}})\sinh {{a}_{f}}-({{\varDelta }_{12}}-{{\varDelta }_{13}})\cosh {{a}_{f}}$ We get tMn by using the expression (23) as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{M}_{t1}}=\frac{-{{\varLambda }_{1}}-{{M}_{s}}a_{f}^{2}\mho }{a_{f}^{2}({{c}_{1}}\cosh {{a}_{f}}+{{c}_{2}}\sinh {{a}_{f}}+{{\varLambda }_{2}}+{{\varLambda }_{3}})} \end{array} \end{aligned} $$

(34)

where

${{\varLambda }_{1}}=\psi _{f}^{2}(\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}})+\varphi _{f}^{2}({{a}_{2}}\cosh {{\varphi }_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}})$,

$\mho ={{c}_{13}}\cosh {{a}_{f}}{{z}_{f}}+{{c}_{14}}\sinh {{a}_{f}}{{z}_{f}}-\frac {1}{{{\tau }_{f}}}\left [ \frac {\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}}}{\psi _{f}^{2}-a_{f}^{2}}+\frac {{{a}_{2}}\cosh {{\varphi }_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}}}{\varphi _{f}^{2}-a_{f}^{2}} \right ]$,

${{\varLambda }_{2}}=\frac {({{\alpha }_{2f}}+{{\alpha }_{1f}})}{(\psi _{f}^{2}-a_{f}^{2})}(\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}})-\frac {2{{\psi }_{f}}{{\alpha }_{2f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{1}}\cosh {{\psi }_{f}}+\sinh {{\psi }_{f}})$,

${{\varLambda }_{3}}=\frac {({{\alpha }_{2f}}+{{\alpha }_{1f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{2}}\cosh {{\varphi }_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}})-\frac {2{{\varphi }_{f}}{{\alpha }_{2f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{3}}\cosh {{\varphi }_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}})$

4.2 Case (ii): Adiabatic-Isothermal Boundary Condition

The lower porous boundary of the combined layer is adiabatic and the upper fluid boundary of the composite layer is isothermal. Using the temperature boundary conditions (26), the distributions ${{\theta }_{f}}({{z}_{f}})$ and ${{\theta }_{p}}({{z}_{p}})$are produced by solving (18) and (21):

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\theta }_{f}}({{z}_{f}})={{A}_{1}}[{{c}_{5}}\cosh {{a}_{f}}{{z}_{f}}+{{c}_{6}}\sinh {{a}_{f}}{{z}_{f}}+{{\varSigma }_{f3}}({{z}_{f}})] \end{array} \end{aligned} $$

(35)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{\theta }_{p}}({{z}_{p}})={{A}_{1}}[{{c}_{7}}\cosh {{a}_{p}}{{z}_{p}}+{{c}_{8}}\sinh {{a}_{p}}{{z}_{p}}+{{\varSigma }_{p3}}({{z}_{p}})] \end{array} \end{aligned} $$

(36)

where ${{\varSigma }_{f3}}({{z}_{f}})={{A}_{1}}[{{\delta }_{11}}-{{\delta }_{12}}+{{\delta }_{13}}-{{\delta }_{14}}],{{\varSigma }_{p3}}({{z}_{p}})={{A}_{1}}[{{\delta }_{15}}-{{\delta }_{16}}]$,

${{\delta }_{11}}=\frac {({{\alpha }_{4f}}{{z}_{f}}+{{\alpha }_{3f}})}{(\psi _{f}^{2}-a_{f}^{2})}(\cosh {{\psi }_{f}}{{z}_{f}}+{{a}_{1}}\sinh {{\psi }_{f}}{{z}_{f}})$,

${{\delta }_{12}}=\frac {2{{\psi }_{f}}{{\alpha }_{4f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{1}}\cosh {{\psi }_{f}}{{z}_{f}}+\sinh {{\psi }_{f}}{{z}_{f}})$,

${{\delta }_{13}}=\frac {({{\alpha }_{4f}}{{z}_{f}}+{{\alpha }_{3f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{2}}\cosh {{\varphi }_{f}}{{z}_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}}{{z}_{f}})$,

${{\delta }_{14}}=\frac {2{{\varphi }_{f}}{{\alpha }_{4f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{3}}\cosh {{\varphi }_{f}}{{z}_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}}{{z}_{f}})$,

${{\delta }_{15}}=\frac {({{\alpha }_{3p}}+{{\alpha }_{4p}}{{z}_{p}})}{(\delta _{p}^{2}-a_{p}^{2})}({{a}_{4}}\cosh {{\delta }_{p}}{{z}_{p}}+{{a}_{5}}\sinh {{\delta }_{p}}{{z}_{p}})$,

${{\delta }_{16}}=\frac {2{{\alpha }_{4p}}{{\delta }_{p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}}({{a}_{5}}\cosh {{\delta }_{p}}{{z}_{p}}+{{a}_{4}}\sinh {{\delta }_{p}}{{z}_{p}})$,

${{\alpha }_{3f}}=R_{If}^{*}-1,{{\alpha }_{4f}}=-2R_{If}^{*},{{\alpha }_{3p}}=-(R_{Ip}^{*}+1),{{\alpha }_{4p}}=-2R_{Ip}^{*}$,

${{c}_{5}}={{c}_{7}}\hat {T}+{{\varDelta }_{21}}-{{\varDelta }_{22}},{{c}_{6}}=\frac {1}{{{a}_{f}}}({{c}_{8}}{{a}_{p}}+{{\varDelta }_{23}}-{{\varDelta }_{24}})$,${{c}_{7}}=\frac {{{\varDelta }_{30}}{{\varDelta }_{25}}-{{\varDelta }_{27}}{{\varDelta }_{29}}}{{{\varDelta }_{28}}{{\varDelta }_{25}}+{{\varDelta }_{26}}{{\varDelta }_{29}}}$,

${{c}_{8}}=\frac {{{\varDelta }_{30}}{{\varDelta }_{26}}+{{\varDelta }_{27}}{{\varDelta }_{28}}}{{{\varDelta }_{29}}{{\varDelta }_{26}}+{{\varDelta }_{25}}{{\varDelta }_{28}}},$ ${{\varDelta }_{20}}=-[{{\delta }_{17}}+{{\delta }_{18}}+{{\delta }_{19}}+{{\delta }_{20}}]$,

${{\delta }_{17}}=\frac {{{\psi }_{f}}({{\alpha }_{4f}}+{{\alpha }_{3f}})}{(\psi _{f}^{2}-a_{f}^{2})}({{a}_{1}}\cosh {{\psi }_{f}}+\sinh {{\psi }_{f}})$,

${{\delta }_{18}}=\left [ \frac {{{\alpha }_{4f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2\psi _{f}^{2}{{\alpha }_{4f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}} \right ](\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}})$,

${{\delta }_{19}}=\frac {{{\varphi }_{f}}({{\alpha }_{4f}}+{{\alpha }_{3f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{3}}\cosh {{\varphi }_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}})$,

${{\delta }_{20}}=[\frac {{{\alpha }_{4f}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2\varphi _{f}^{2}{{\alpha }_{4f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}]({{a}_{2}}\cosh {{\varphi }_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}})$,

${{\varDelta }_{21}}=\hat {T}\left [ \frac {{{\alpha }_{3p}}{{a}_{4}}}{(\delta _{p}^{2}-a_{p}^{2})}-\frac {2{{\alpha }_{4p}}{{\delta }_{p}}{{a}_{5}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}} \right ]$,

${{\varDelta }_{22}}=\frac {{{\alpha }_{3f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2{{\psi }_{f}}{{a}_{1}}{{\alpha }_{4f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}+\frac {{{a}_{2}}{{\alpha }_{3f}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2{{\varphi }_{f}}{{a}_{3}}{{\alpha }_{4f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}$,

${{\varDelta }_{23}}=[\frac {{{\alpha }_{4p}}}{(\delta _{p}^{2}-a_{p}^{2})}-\frac {2\delta _{p}^{2}{{\alpha }_{4p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}}]{{a}_{4}}+\frac {{{a}_{5}}{{\alpha }_{3p}}}{(\delta _{p}^{2}-a_{p}^{2})}$,

${{\varDelta }_{24}}=\frac {{{\alpha }_{3f}}{{\psi }_{f}}{{a}_{1}}+{{\alpha }_{4f}}}{(\psi _{f}^{2}-a_{f}^{2})}-\frac {2{{\alpha }_{4f}}\psi _{f}^{2}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}+\frac {{{\alpha }_{3f}}{{\varphi }_{f}}{{a}_{3}}+{{\alpha }_{4f}}{{a}_{2}}}{(\varphi _{f}^{2}-a_{f}^{2})}-\frac {2{{a}_{2}}{{\alpha }_{4f}}\varphi _{f}^{2}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}$,

${{\varDelta }_{25}}=\cosh {{a}_{p}},{{\varDelta }_{26}}=\sinh {{a}_{p}}$,

${{\varDelta }_{27}}=-\frac {{{\alpha }_{3p}}-{{\alpha }_{4p}}}{(\delta _{p}^{2}-a_{p}^{2})}({{a}_{4}}\cosh {{\delta }_{p}}-{{a}_{5}}\sinh {{\delta }_{p}})+\frac {2{{\delta }_{p}}{{\alpha }_{4p}}}{{{(\delta _{p}^{2}-a_{p}^{2})}^{2}}}({{a}_{5}}\cosh {{\delta }_{p}}-{{a}_{4}}\sinh {{\delta }_{p}})$,

${{\varDelta }_{28}}={{a}_{f}}\hat {T}\sinh {{a}_{f}},{{\varDelta }_{29}}={{a}_{p}}\cosh {{a}_{f}}$,

${{\varDelta }_{30}}={{\varDelta }_{20}}-{{a}_{f}}({{\varDelta }_{21}}-{{\varDelta }_{22}})\sinh {{a}_{f}}-({{\varDelta }_{23}}-{{\varDelta }_{24}})\cosh {{a}_{f}}$.

We get tMn from (23) as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {{M}_{t2}}=\frac{-{{\varLambda }_{1}}-{{M}_{s}}a_{f}^{2}\mho }{a_{f}^{2}({{c}_{5}}\cosh {{a}_{f}}+{{c}_{6}}\sinh {{a}_{f}}+{{\varLambda }_{4}}+{{\varLambda }_{5}})} \end{array} \end{aligned} $$

(37)

where ${{\varLambda }_{4}}=\frac {({{\alpha }_{4f}}+{{\alpha }_{3f}})}{(\psi _{f}^{2}-a_{f}^{2})}(\cosh {{\psi }_{f}}+{{a}_{1}}\sinh {{\psi }_{f}})-\frac {2{{\psi }_{f}}{{\alpha }_{4f}}}{{{(\psi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{1}}\cosh {{\psi }_{f}}+\sinh {{\psi }_{f}})$,

${{\varLambda }_{5}}=\frac {({{\alpha }_{4f}}+{{\alpha }_{3f}})}{(\varphi _{f}^{2}-a_{f}^{2})}({{a}_{2}}\cosh {{\varphi }_{f}}+{{a}_{3}}\sinh {{\varphi }_{f}})-\frac {2{{\varphi }_{f}}{{\alpha }_{4f}}}{{{(\varphi _{f}^{2}-a_{f}^{2})}^{2}}}({{a}_{3}}\cosh {{\varphi }_{f}}+{{a}_{2}}\sinh {{\varphi }_{f}})$.

5 Results and Discussion

The tMns for two cases of thermal boundary conditions ${{M}_{t1}}$ and ${{M}_{t2}}$ are obtained as expressions of the depth ratio $\hat {d}$, the porous parameter $\beta$, the thermal ratio $\hat {T}$, the solutal ratio $\hat {S}$, sMn ${{M}_{s}}$ and the Chandrasekhar number ${{Q}_{f}}$, the horizontal wave numbers ${{a}_{f}}$ and ${{a}_{p}}$, the diffusivity ratio ${{\tau }_{f}} and {{\tau }_{p}}$, and $R_{If}^{*}$ and $R_{Ip}^{*}$ the modified internal Rayleigh numbers for region 1 and region 2. The thermal boundary conditions taken are adiabatic-adiabatic and that the combined layer is horizontally enclosed by the adiabatic boundaries and adiabatic-isothermal, the lower porous boundary of the composite system is adiabatic, and the upper fluid boundary of the composite system is isothermal. These tMns ${{M}_{t}}$ are drawn versus the depth ratio$\hat {d}$ using Mathematica software. The other parameters are ${{a}_{f}}=0.5,{{Q}_{f}}=10$, $\beta =1.0,\hat {\mu }=2,\hat {S}=\hat {T}=1,{{\tau }_{f}}={{\tau }_{p}}=0.25,{{M}_{s}}=10,R_{If}^{*}=1$ and $R_{Ip}^{*}=1$, the effects of the various parameters are described in detail and represented in the graphs below.

Figure 2 represents the comparison of ${{M}_{t1}}$ and ${{M}_{t2}}$, where ${{M}_{t}}$ is the dependent variable and $\hat {d}$, the depth ratio, is the independent variable. The tMn decreases up to some value of the depth ratio, and later it increases as the value of the depth ratio also increases. This behavior is qualitatively the same for both types of thermal boundary combination (TBC). It is interesting to note that for larger values of depth ratios, the Marangoni numbers coincide and no change in them for $\hat {d}\ge 2$, i.e., for porous layer dominant (in depth) systems which is physically impressive as the TBC at the boundary of the porous layer is changed. But for the smaller depth ratio values, the thermal Marangoni number for case (i) is smaller than that for case (ii), indicating that the system with case (i) TBC is more stable.

Fig. 2

Comparison of tMn for case (i) adiabatic-adiabatic and case (ii) adiabatic-isothermal

For both situations of TBCs, the effects of the Chandrasekhar number ${{Q}_{f}}$ on double-diffusive Marangoni convection (DDMC) (DDMC) are shown in Fig. 3. The values of ${{Q}_{f}}$ that were used were 1, 10, and 100. The curves are diverging, showing that ${{Q}_{f}}$ is more prominent at higher depth ratios, i.e., for the porous layer dominant composite system (PDCS). Because an increase in the value of ${{Q}_{f}}$ raises the tMns for a certain depth ratio, the DDC can be advanced by lowering the values of ${{Q}_{f}}$, and the system can be destabilized. This parameter’s effect is analogous to that of TBCs.

Fig. 3

Variations of ${{Q}_{f}}=1,10,100$ on tMn when ${{a}_{f}}=0.5,\beta =1.0,\hat {\mu }=2,\hat {S}=\hat {T}=1,{{\tau }_{f}}={{\tau }_{p}}=0.25,{{M}_{s}}=10,R_{If}^{*}=1$ and$R_{Ip}^{*}=1$

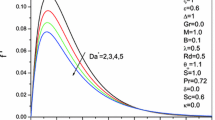
The effect of a modified internal Rayleigh number $R_{If}^{*}$ on the tMn is shown in Fig. 4 for both the TBCs $R_{If}^{*}=-1,0$ and 1. For larger depth ratio values, i.e., for porous layer dominant composite system (PDCS), the curves diverge, reflecting the importance of the modified internal Rayleigh number. The tMn increases when the value of $R_{If}^{*}$ is increased, that is, from sink to source, for a certain depth ratio. As a result, the DDMC in the presence of a magnetic field can be delayed by raising the value of $R_{If}^{*}$. As a result, the heat absorption stabilizes the system. For TBCs, the effect of this parameter is comparable.

Fig. 4

Variations of $R_{If}^{*}=-1,0,1$ on tMn when ${{a}_{f}}=0.5,{{Q}_{f}}=10,\beta =1.0,\hat {\mu }=2,\hat {S}=\hat {T}=1,{{\tau }_{f}}={{\tau }_{p}}=0.25,{{M}_{s}}=10$ and$R_{Ip}^{*}=1$

The effect of a modified internal Rayleigh number for porous layer $R_{Ip}^{*}$ on the tMn is shown in Fig. 5 for $R_{Ip}^{*}=-1,0$ and 1. The Marangoni number grows as the amount of $R_{Ip}^{*}$ is increased from sink to source; hence, the DDMC in the presence of a magnetic field can be delayed by raising the value of $R_{Ip}^{*}$. As a result, the heat absorption stabilizes the system. This parameter has the same effect in both scenarios of TBCs. Also, as shown in the diagram, this parameter is effective for some modest depth ratios, that is, for PDCS in both scenarios of TBCs.

Fig. 5

Variations of $R_{Ip}^{*}=-1,0,1$ for porous region on tMn when ${{a}_{f}}=0.5,{{Q}_{f}}=10,\beta =1.0,\hat {\mu }=2,\hat {S}=\hat {T}=1,{{\tau }_{f}}={{\tau }_{p}}=0.25,{{M}_{s}}=10$ and $R_{If}^{*}=1$

The effect of solute Marangoni number ${{M}_{s}}$ on the Marangoni number is similar for both the cases of TBCs, which is exhibited in Fig. 6 for ${{M}_{s}}=5,10$ and 50. On increasing the values of ${{M}_{s}}$, the tMn for DDMC in the presence of magnetic field increases; hence, the DDMC can be delayed by increasing the values of ${{M}_{s}}$. The diverging curves reveal that the effect of sMn is intensive for larger values of depth ratios, that is, for PDCS. The effect of this parameter is comparable to the cases of TBCs.

Fig. 6

Variations of ${{M}_{s}}=5,10,50$ on tMn when ${{a}_{f}}=2.5,{{Q}_{f}}=10,\beta =1.0,\hat {\mu }=2,\hat {S}=\hat {T}=1,{{\tau }_{f}}={{\tau }_{p}}=0.25,R_{If}^{*}=1$ and $R_{Ip}^{*}=1$

6 Conclusion

In the current study, the impact of a heat source and magnetic field on onset convection is thoroughly investigated for two different boundary configurations. Because of this, the composite layer system is stable and can be used in adiabatic-adiabatic thermal boundary conditions, where convection needs to be regulated. The following are the key findings from the current study:

• (i) When compared to the case (ii) thermal boundary condition, the tMn for the case (i) thermal boundary condition is large. As a result, in the case of case (i), the fluid-porous system is stable and can be used in circumstances where convection must be controlled.

• (ii) All the physical parameters are effective for the larger values for depth ratios that are for the PDCS.

• (iii) In the present study, by increasing the values of the Chandrasekhar number ${{Q}_{f}}$, the modified internal Rayleigh numbers $R_{If}^{*}$, $R_{Ip}^{*}$, and the solute Marangoni number ${{M}_{s}}$ in the presence of magnetic field, the thermal Marangoni numbers, i.e., to stabilize the system, so the onset of DDMC is delayed.

• (iv) The DDMC in the combined system can be controlled by selecting the proper values for the physical parameters. Results are in good accordance with earlier work.