Non-iterative Stress Projection Method for Rate-Independent Plasticity

Abstract

A fully-explicit stress integration method is comprehensively discussed via finite element analyses using three different classes of continuum plasticity models, i.e., anisotropic yield function, anisotropic hardening, and continuum damage model. A unified but straightforward formulation covers a wide range of rate-independent plasticity models. High accuracy, numerical robustness, and great efficiency are achieved through the use of generalized effective plastic strain and stress projection equations. In order to estimate the stress integration quality, an associated variable mapping technique, namely, the precision map, is introduced. Based on the precision map study, the current fully-explicit integration exhibits excellent accuracy. Furthermore, this non-iterative stress calculation reduces the computation cost by about 50% compared to conventional iterative stress update algorithms.

1 Introduction

Numerical simulations involving metal plasticity significantly contribute to the analysis and optimization of manufacturing processes in various industries. The modeling of advanced materials demands complex formulations to reproduce unique plastic deformation mechanisms that are not well described by classical approaches. However, inefficient computation, poor numerical robustness (or stability), and low-stress integration quality are obstacles to more widespread use of these advanced formulations.

Conventional stress integration methods (algorithms) show superb performances in solving non-linear problems involving plasticity. Iterative (implicit) solution-finding approaches, nevertheless, lead to conditional success in stress integration depending on the model formalisms, deformation modes, and simulation analysis parameters. In addition, the classical integration strategies are limited by the shortcomings of the root-finding process, namely, the Newton-Raphson method. Over the last decade, numerous efforts have been made such as the line-search method, the residual value control, etc., in order to enhance the numerical performance of these algorithms. However, such treatments are, in general, accompanied by increased computation costs.

Fully-explicit stress integration approaches are featured with two primary advantages such as high computation speed and numerical robustness. The critical drawbacks, e.g., poor integration quality and conditional stability mainly stem from the uncertain fulfillment of the yield condition. Rossi et al. [1] initially utilized a numerical technique, so-called stress projection, to get the unconditional yield condition satisfaction. Independently, Yoon and Barlat [2] suggested the non-iterative stress projection method and applied it to implicit as well as explicit finite element analyses resulting in impressive performances.

In this article, the non-iterative stress projection method is briefly introduced. The stress integration quality is comparatively validated by means of the mapping of a fidelity parameter on a yield locus. Finally, its performance is estimated via finite element simulations using a variety of advanced plasticity models.

2 Non-iterative Stress Projection Method

Fig. 1.

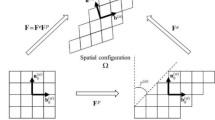
Graphical description of the non-iterative stress projection method [2]

The non-iterative stress projection method features (1) a direct stress integration using elastoplastic tangent operators, (2) a positive-definite effective plastic strain for high numerical robustness, and (3) a stress projection for yield condition fulfillment. Figure 1 displays the schematic description of the non-iterative stress projection method.

The stress tensor is instantly updated on the basis of the elastoplastic constitutive law for the plastic deformation state.

$$ {{\varvec{\upsigma}}}_{{{\text{n}} + \frac{1}{2}}} = {{\varvec{\upsigma}}}_{{\text{n}}} + \Delta {{\varvec{\upsigma}}}_{{{\text{n}} + \frac{1}{2}}} $$

(1a)

$$ \Delta {{\varvec{\upsigma}}}_{{{\text{n}} + \frac{1}{2}}} = {\boldsymbol{\mathcal{C}}}_{{\text{n}}}^{{{\text{ep}}}} :\Delta {{\varvec{\upvarepsilon}}}_{{{\text{n}} + 1}} $$

(1b)

where ${\boldsymbol{\mathcal{C}}}_{\mathrm{n}}^{\mathrm{ep}}$ denotes an elastoplastic tangent modulus. The index (n + 1/2) indicates that the intermediate stress is not a final solution but needed to be corrected later. The plastic strain is approximated using the additive decomposition of the total strain, and the above-calculated stress increment.

$$ \Delta {{\varvec{\upvarepsilon}}}_{{{\text{n}} + \frac{1}{2}}}^{{\text{p}}} \approx \Delta {{\varvec{\upvarepsilon}}}_{{{\text{n}} + 1}} - {\boldsymbol{\mathcal{S}}}^{{\text{e}}} :\Delta {{\varvec{\upsigma}}}_{{{\text{n}} + \frac{1}{2}}} $$

(2)

${\varvec{\mathcal{S}}}^{\mathrm{e}}$ represents the elastic compliance tensor. The positive-definite effective strain increment is acquired from the scalar product of the flow rule.

$$ \Delta {\overline{\upvarepsilon }}_{{{\text{n}} + \frac{1}{2}}} = \sqrt {\frac{{\Delta {{\varvec{\upvarepsilon}}}_{{{\text{n}} + 1/2}}^{{\text{p}}} :\Delta {{\varvec{\upvarepsilon}}}_{{{\text{n}} + 1/2}}^{{\text{p}}} }}{{\frac{{\partial {\overline{\upsigma }}_{{{\text{n}} + 1/2}} }}{{\partial {{\varvec{\upsigma}}}_{{{\text{n}} + 1/2}} }}:\frac{{\partial {\overline{\upsigma }}_{{{\text{n}} + 1/2}} }}{{\partial {{\varvec{\upsigma}}}_{{{\text{n}} + 1/2}} }}}}} $$

(3)

The effective plastic strain and internal state variables are explicitly updated making use of the effective strain increment (Eq. (3)).

$$ {\overline{\upvarepsilon }}_{{{\text{n}} + 1}} = {\overline{\upvarepsilon }}_{{\text{n}}} + \Delta {\overline{\upvarepsilon }}_{{{\text{n}} + \frac{1}{2}}} $$

(4)

$$ {{\bf{r}}_{{\rm{n}} + 1}} = {{\bf{r}}_{\rm{n}}} + \frac{{{\rm{d}}{\bf{r}}}}{{{\rm{d}}\bar \upvarepsilon }}\Delta {\bar \upvarepsilon _{{\rm{n}} + \frac{1}{2}}}$$

(5)

Finally, the intermediate updated stress (Eq. (1a)) is projected onto the updated flow stress.

$$ {{\varvec{\upsigma}}}_{{{\text{n}} + 1}} = \frac{{{\text{H}}\left( {{\overline{\upvarepsilon }}_{{{\text{n}} + 1}} } \right)}}{{{\overline{\upsigma }}\left( {{\mathbf{r}}_{{{\text{n}} + 1}} ,{{\varvec{\upsigma}}}_{{{\text{n}} + 1/2}} } \right)}}{{\varvec{\upsigma}}}_{{{\text{n}} + \frac{1}{2}}} $$

(6)

Note that the current stress projection expression is available only when the yield condition is a homogeneous function.

3 Precision Map

In this section, the precision map is introduced to intuitively validate the stress integration quality of the non-iterative stress projection method (NSPM) for an imposed time (strain) increment through a comparative study with conventional iterative stress update algorithms, namely, the closest point projection method (CPPM) and the cutting plane method (CPM). For the accuracy validation, the R-value, a representative material anisotropy parameter, is valid only for uniaxial and balanced biaxial modes. Alternatively, the square root of the scalar product of the yield surface gradient is adopted as the fidelity parameter to cover entire deformation modes.

$$\Omega = \sqrt {\frac{{{\partial }{\overline{\sigma }}}}{{\partial {{\varvec{\upsigma}}}}}:\frac{{\partial {\overline{\sigma }}}}{{\partial {{\varvec{\upsigma}}}}}} $$

(7)

The precision map records the fidelity parameters on the normalized yield locus for numerous deformation modes. The corresponding plane stress tensors are defined by means of trigonometrical functions. To obtain the entire stress states on the outline of a yield surface $\left({\upsigma }_{12}=0\right)$, a primary angle $\left({\uptheta }_{1}\right)$ which is the argument of the trigonometrical functions varies from 0° to 360°. The inside of a yield surface is filled out by rotating a plane stress tensor on the outline from 0° to 45° using a secondary angle $\left({\uptheta }_{2}\right)$. Finally, 16,606 data points representing the fidelity parameter values are generated for a single map. Individual data points are determined after the stand-alone simulations where the major strain component is discretized by a prescribed boundary condition, and time increment, and the minor components are specified after the manipulation of the generalized Hooke’s law and a reference stress tensor.

Fig. 2.

Fidelity parameter values (Eq. (7)) of Yld2000-2d calibrated for AA2090-T3 mapped on the yield locus where the values are obtained from (a) reference stress state, (b) CPPM (fully implicit), (c) CPM (semi-explicit), (d) NSPM (fully explicit)

An aluminum-lithium alloy (AA2090-T3) characterized by a non-quadratic anisotropic yield function (Yld2000-2d) was selected for this study [2]. For the precision mapping, a material point is subjected to 0.1 true strain (ε_true = 0.1) for each deformation mode and analyzed with a fixed time increment (Δt = 0.01). Thereby, the major strain increment (Δε_major = 0.001) is evenly imposed at each analysis step. Note that the strain increment, in general, ranges from 10^–6 to 10^–3 for implicit finite element analysis.

Figure 2 shows the fidelity parameters at every plane stress state after corresponding simulations using Yld2000-2d. The magnitude of the parameter is marked blue varying its intensity. The reference value is obtained from the stress states prescribed by the trigonometrical functions before running simulations in virtue of the consistency of yield surface gradients. Due to the numerical error accumulated during a simulation, the desired stress tensors are frequently lost after passing stress integration processes. The discrepancy in the precision maps depends on the integration schemes. According to the mapping study, NSPM results in the exactly same fidelity parameter pattern as CPPM. The mapping pattern by CPM is apart from the others.

The distinction between the maps in Fig. 2 is visualized by mapping the relative errors on the yield condition, so-called the error map (See Fig. 3). The relative error is calculated below.

$$ {\text{ERROR}} = \frac{{\left| {{\Omega }_{{{\text{ref}}}} - {\Omega }} \right|}}{{{\Omega }_{{{\text{ref}}}} }} \times 100{\text{ \% }} $$

(8)

Fig. 3.

Relative error patterns which represent the gaps between the reference value and the fidelity values from (a) CPPM (fully implicit), (b) CPM (semi-explicit), and (c) NSPM (fully explicit)

NSPM shows the same maximum error value (0.3%) as that of CPPM. In contrast, CPM results in the highest error (9.3%). This implies that the stress integration quality of NSPM is very close to CPPM even with such a coarse strain increment (Δε_major = 10^–3). The error deviation between the considered integration methods may differ depending on the magnitude of the strain increment and the material anisotropy. In other words, for the more refined strain increment, CPM will give the same accuracy as the others. The precision map indirectly exhibits the accuracy of stress integration methods for a prescribed strain increment, which is very close to the displacement-controlled finite element analysis. The fidelity parameter can be replaced with other variables for various purposes. One may find the original source code at [7].

4 Finite Element Analysis

In this section, the numerical performance of NSPM is discussed via finite element simulations using three classes of plasticity models, i.e., anisotropic yield function (Yld200-2d), anisotropic hardening model (Homogeneous anisotropic hardening – HAH₂₀), and continuum damage model (Gurson-Tvergaard-Needleman – GTN). Detailed descriptions of model coefficients and finite element modeling are found in the works [2,3,4]. The plasticity models are implemented into the finite element program, namely, Abaqus 6.20/explicit through the vectorized user-defined material (VUMAT) subroutine. For objectivity, simulation results of NSPM are compared to those of CPPM and CPM in each sub-section. The used VUMAT subroutine code is available at [8].

4.1 Deep Drawing: Yld2000-2d

A non-quadratic anisotropic yield function (Yld2000-2d) is exploited to reproduce the material anisotropy of AA2090-T3 in the deep drawing simulation.

Fig. 4.

Effective stress (SDV2) distribution of Yld2000-2d in deep drawing explicit finite element simulations integrated using (a) CPPM (fully-implicit), (b) CPM (semi-explicit), and (c) NSPM (fully-explicit)

Figure 4 shows the distribution of effective stress after explicit deep drawing simulation. The stress prediction by NSPM is identical to the other methods. The obtained earing profiles are completely overlapped with one another (See Fig. 5(a)). The computation time with NSPM is reduced by as much as 64% compared to CPPM although the latter requires only 1 or 2 iterations for algorithmic convergence (See Fig. 5(b)). The high efficiency of NSPM likely results from the simple formulation in addition to the zero iteration.

Fig. 5.

(a) Earing profiles after deep drawing simulations and (b) computation costs obtained from CPPM (fully implicit), CPM (semi-explicit), and NSPM (fully explicit)

4.2 S-rail Forming: HAH₂₀

NSPM is also available for any type of anisotropic hardening when a morphological change of yield surface is incorporated in an elastoplastic tangent operator. The morphologic component contributes to the instant but an accurate calculation of the effective strain increment in the present method as well as other algorithms. A distortional plasticity hardening model (HAH₂₀) [5] is used for plasticity modeling of dual-phase steel (DP780) under non-proportional loading conditions and applied to an industrial scale simulation, namely, the S-rail forming.

Fig. 6.

Effective stress (SDV2) distribution of HAH₂₀ in S-rail forming explicit finite element simulations integrated using (a) CPPM (fully-implicit), (b) CPM (semi-explicit), and (c) NSPM (fully-explicit)

NSPM results in an effective stress distribution in Fig. 6 in excellent agreement with those obtained from CPPM and CPM after the forming simulations. Figure 7(a) indicates that all the springback profiles are in excellent agreement as well. Figure 7(b) shows that the analysis time with NSPM is reduced by 46% without loss of accuracy after forming and springback simulations (See Fig. 7(b)). In this application, CPPM and CPM require 2 or 3 iterations to complete the stress integration.

Fig. 7.

(a) Springback profiles after S-rail forming simulations and (b) computation costs obtained from CPPM (fully-implicit), CPM (semi-explicit), and NSPM (fully-explicit)

4.3 Hole Expansion: Modified GTN

The modified GTN model [6] is employed for failure prediction in a conical hole expansion simulation. The model coefficients are calibrated based on the fracture behavior of dual-phase steel (DP980).

Fig. 8.

Effective stress (SDV2) distribution of the modified GTN in the hole expansion explicit finite element simulations integrated using (a) CPPM (fully-implicit), (b) CPM (semi-explicit), and (c) NSPM (fully-explicit)

Figure 8 exhibits the equivalent stress of the modified GTN when the strain localization initiates. The stress pattern and the localization positions show reasonable agreement. The deviations among the load-displacement curves in Fig. 9(a) might result from the extraordinarily large strain increment when the localization is initiated. CPPM demands 3 to 7 iterations for the algorithm convergence, and CPM 2 to 5. Consequently, NSPM boosts the simulation time by 60%.

Fig. 9.

(a) Load-displacement curves in conical hole expansion simulations and (b) computation costs obtained with CPPM (fully implicit), CPM (semi-explicit), and NSPM (fully explicit)

5 Conclusions

In this article, the non-iterative stress projection method (NSPM) is comprehensively studied, from formulation to application. For a strict evaluation of the integration quality, a precision mapping technique is introduced. NSPM exhibits outstanding numerical performance in terms of computation speed, stress integration accuracy, and robustness. The main results of this work are summarized as follows:

• A chronic shortcoming of the fully-explicit stress integration method is resolved by employing the stress projection technique.

• The stress integration quality of NSPM is comparable to that of the return mapping-based stress update algorithm according to the precision map results.

• The excellent numerical performance of NSPM is qualitatively demonstrated based on a variety of finite element simulations and plasticity models.