Identification of Damage in Truss and Beam Structures Based on Flexibility Matrix

Abstract

In this work, we propose a numerical strategy to detect damages in truss and beam structures exploiting lowest frequencies and mode shapes that are employed to calculate the flexibility matrix. In particular, for truss structures, the modal strain difference between damaged and healthy structures is used to identify the element characterized by the highest value of strain change, which corresponds to the most likely damaged element in the structure. Conversely, for beam structures, the highest value of modal curvature change is used as an index of element damage. Both procedures are validated using pseudo-experimental data accounting for noise pollution in mode shapes components.

1 Introduction

Recent bridge collapses in Italy (as Morandi bridge in 2018 and Massa Carrara bridge in 2020) have raised the attention of the stakeholders and of the scientific community on the importance of early detection of damages in civil engineering structures [1, 2]. Within this context, the development of robust and reliable Structural Health Monitoring (SHM) techniques is becoming of central importance. Among the available SHM strategies, vibration-based (or dynamic) techniques use recorded structural vibration responses to obtain an estimate of structural modal parameters such as frequencies, mode shapes and damping ratios. When during the monitoring phase, these parameters show a significant change, this variation may be attributed to the occurrence of a possible damage in the structure [3]. Numerous algorithms and procedures have been proposed in literature to interpret changes in modal parameters in order to detect, localize and assess the severity of damage [4].

In this paper, we propose and discuss an algorithm for damage detection and localization in planar truss and beam structures. The algorithm is based on the flexibility matrix, which is accurately approximated by the lowest frequencies and mode shapes of a structure. Such modal parameters can be easily identified by means of experimental and/or operational modal analysis techniques applied to in-field measurements [5, 6]. In particular, for the truss structures, the techniques exploit the variation/increase in strain, with respect to the intact state, due to the insurgence of damage in bar (reduction in modulus of elasticity and/or cross-sectional area). From the flexibility matrix, where each column represents displacement patterns for the structure due to unit forces applied to the corresponding degrees of freedom, we calculate the modal strains. Following this approach, the element with the largest variation in strain before and after damage occurrence is identified as the damaged element [7, 8]. A similar idea is applied to beam structures. In this case, from the displacement patterns extracted from the approximate expression of the flexibility matrix, modal curvature changes between the healthy and damaged structure are evaluated [9]. The largest values of curvature change are then used to identify the presence and location of damage [10, 11].

To prove the reliability of the proposed method, simply supported truss and beam structures are studied, considering several damage locations and intensities. To replicate an on-field procedure, modal data are corrupted with increasing levels of noise to test the robustness of the proposed algorithm. The procedure shows an accurate identification of all the damaged elements also in presence of a high level of noise. Only for very low intensity of damage, some elements in the truss and beam structures are not identified.

2 Damage Detection Method

Let us consider a generic structure with n degrees of freedom. Its flexibility matrix $\textbf{F}$ can be expressed in terms of the modal matrix $\mathbf {\Phi }$ and spectral matrix $\mathbf {\Omega }$ as:

$$\begin{aligned} \textbf{F}=\mathbf {\Phi }(\mathbf {\Omega }^\mathrm{{-1}})\mathbf {\Phi }^\mathrm{{T}}=\sum _{i=1}^{n}{\frac{1}{\omega _{i}^{2}}}\mathbf {\Phi }_{i}\mathbf {\Phi }_{i}^\mathrm{{T}} \end{aligned}$$

(1)

being $\mathbf {\Phi }_{i}$ the i-th column of matrix $\mathbf {\Phi }$, $\omega _{i}$ the i-th circular frequency and symbol $\textrm{T}$ the transpose operator. Due to the rapid convergence of the flexibility matrix for increasing natural frequencies and mode shapes, its computation can be approximated considering the first m ($<n$) lower modes and frequencies of the structure as:

$$\begin{aligned} \textbf{F}\approx \sum _{i=1}^{m}{\frac{1}{\omega _{i}^{2}}}\mathbf {\Phi }_{i}\mathbf {\Phi }_{i}^\mathrm{{T}} \end{aligned}$$

(2)

Note that each column of the flexibility matrix represents a displacement pattern of the structure corresponding to a unit force applied at the corresponding degree of freedom, [7]. Hence, it is possible to extract from the $j-$th column of the flexibility matrix, the displacement vector $\textbf{u}_{ij}$, which collects the displacement components of the $i-$th element as:

$$\begin{aligned} \textbf{u}_{ij}=\textbf{T}_{i}\begin{bmatrix} f_{1j} \\ \vdots \\ f_{nj}\\ \end{bmatrix} \qquad i=1..n_e \qquad j=1..n \end{aligned}$$

(3)

where $\textbf{T}_{i}$ is the $n_{dof} \times n$ boolean operator used to extract from the $j-$th column of flexibility matrix $\begin{bmatrix} f_{1j}&...&f_{nj} \end{bmatrix}^\textrm{T}$ the displacement vector $\textbf{u}_{ij}$, being $n_{dof}$ the number of degrees of freedom of each element in which the structure is divided.

Since damage in a structure leads to an increase in flexibility, such variation in flexibility is employed to define the indexes to detect damage in a structure. In what follows, we specify the indexes utilized for trusses and beam structure, respectively.

2.1 Damage Index for Trusses

We consider a planar truss structure with $n_e$ bars, where each bar has two degrees of freedom per node (horizontal displacement, u, and vertical displacement, v). The $4 \times 1$ vector $\textbf{u}_{ij}$ collects the nodal displacements $\begin{bmatrix} \bar{u}_1&\bar{v}_1&\bar{u}_2&\bar{v}_2 \end{bmatrix}^\textrm{T}$ of the $i-$th bar element for the $j-$th column of the flexibility matrix. Modal strain $\epsilon _{ij}$ can be evaluated from the displacement vector, Eq. (3), as

$$\begin{aligned} \epsilon _{ij}=\textbf{R}_{i}\textbf{u}_{ij} \end{aligned}$$

(4)

where $\textbf{R}_{i}$ is the $1 \times 4$ rotation matrix. Modal strains of the healthy truss are collected in the $\textbf{MSH}$ matrix of dimensions $n_e \times n$.

The same procedure is applied to the damaged structure: we evaluate the lowest m circular frequencies and mode shapes, calculate the approximate expression of the flexibility matrix, Eq. (2), extract the n displacement vectors, Eq. (3), and determine the strains for all the elements, Eq. (4). The modal strains of the damaged structure are collected in the $n_e \times n$ $\textbf{MSD}$ matrix. The damage index is thus introduced as follows. Given the modal strain change matrix $\textbf{MSC}$, as

$$\begin{aligned} \textbf{MSC}=\textbf{MSD}-\textbf{MSH} \end{aligned}$$

(5)

for each row the maximum of the absolute value of $\textbf{MSC}$ is selected and collected in the $n_e \times 1$ modal strain change vector denoted as $\textbf{msc}$:

$$\begin{aligned} \textbf{msc}=\textrm{max}_{i=1..ne}|\textbf{MSC}| \end{aligned}$$

(6)

According to this approach, the most likely damaged element is identified as the bar corresponding to the highest value of strain change in vector $\textbf{msc}$, Eq. (6).

2.2 Damage Index for Beams

Let us consider a generic beam structure modelled under the Euler-Bernoulli hypothesis, thus neglecting the shear deformation. The beams are divided in $n_e$ elements with two degrees of freedom per node (deflection, v, and rotation, $\phi$). Indicating with $\textbf{N}=\textbf{N}(x)$ the $4 \times 1$ vector of the cubic shape functions [12], being x the local coordinate and with $\textbf{u}_{ij}$ the $4 \times 1$ vector of nodal displacements $\begin{bmatrix} \bar{v}_1&\bar{\phi }_1&\bar{v}_2&\bar{\phi }_2\end{bmatrix}^\textrm{T}$, the approximate expressions of the displacement and curvature for the $i-$th element read:

$$\begin{aligned} v_{ij}=\textbf{N}^\mathrm{{T}}\textbf{u}_{ij} \end{aligned}$$

(7)

$$\begin{aligned} v_{ij}''=\textbf{B}^\mathrm{{T}}\textbf{u}_{ij} \end{aligned}$$

(8)

where $\textbf{B}$ is the vector of the second-order spatial derivatives of the shape functions. As in the case of truss structures, the lowest frequencies and mode shape vectors allow to obtain an approximate expression of the flexibility matrix $\textbf{F}$ according to Eq. (2). From the columns of the flexibility matrix, the displacement vectors $\textbf{u}_{ij}$ are derived, Eq. (3).

The displacement vectors are evaluated for the damaged and healthy structure, namely $\textbf{u}_{ij}^\mathrm{{D}}$ and $\textbf{u}_{ij}^\mathrm{{H}}$, respectively. Following the approach described in [9], the modal curvature change $MCC_{ij}$ is calculated for each element and each column of the flexibility matrix:

$$\begin{aligned} MCC_{ij} = \varDelta \textbf{u}_{ij}^\mathrm{{T}} \left[ \int _0^{L{_{i}}}\textbf{B}^\mathrm{{T}}\textbf{B}\textrm{d}x \right] \varDelta \textbf{u}_{ij} \end{aligned}$$

(9)

where $L_{i}$ is the length of the $i-$th element and $\varDelta \textbf{u}_{ij}$ is defined as

$$\begin{aligned} \varDelta \textbf{u}_{ij}=\textbf{u}_{ij}^\mathrm{{D}}-\textbf{u}_{ij}^\mathrm{{H}} \end{aligned}$$

(10)

For each element, we have n evaluations of the curvature change, Eq. (9), which are collected in $\textbf{MCC}$ matrix of dimensions $n_e \times n$. For each row of $\textbf{MCC}$ the maximum value is determined and collected in the $n_e \times 1$ modal curvature change denoted as $\textbf{mcc}$:

$$\begin{aligned} \textbf{mcc}=\textrm{max}_{i=1..n_e}|\textbf{MCC}| \end{aligned}$$

(11)

Similarly to the approach proposed for the truss structures, the most likely damaged element is identified as the element corresponding to the highest value of curvature change in vector $\textbf{mcc}$, Eq. (11).

3 Numerical Applications

In this section, the identification procedure is applied to two structures: a truss structure and a simply supported beam.

Fig. 1.

Simply-supported truss structure under study. Dimensions in meters.

3.1 Truss Structure

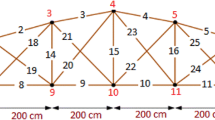
The simply-supported truss under consideration is represented in Fig. 1, [13]. The structure is characterized by $n_e = 25$ elements and 12 nodes for a total of $n=21$ DOFs. For all elements, the modulus of elasticity E and the material density $\rho$ are assumed equal to 200 GPa and 7800 kg/$\textrm{m}^3$, respectively. The cross sectional area of each element is equal to $A_1 = 1.8 \times 10^3$ $\textrm{mm}^2$ for the elements from 1 to 6, $A_2 = 1.5 \times 10^3$ $\textrm{mm}^2$ for the elements from 7 to 12, $A_3 = 1.0 \times 10^3$ $\textrm{mm}^2$ for the elements from 13 to 17 and $A_4 = 1.2 \times 10^3$ $\textrm{mm}^2$ for the diagonal elements (from 18 to 25). The change in stiffness due to damage is modelled as a reduction in the modulus of elasticity of the elements. Each truss bar is damaged with six increasing levels of damage d: $5\%$, $10\%$, $30\%$, $50\%$, $70\%$ and $90\%$. In order to check for the robustness of the procedure, the reduction of the modulus of elasticity is imposed to each element e in turn. Additionally, four noise levels are considered: no noise, $1\%$, $2\%$ and $3\%$. In this study, mode shape components are polluted by noise, while the frequencies are not affected by noise. For the calculation of the flexibility matrix, we utilize the first $m = 4$ natural frequencies and mode shapes of the structure before and after damage.

Identification results for zero noise level are collected in Table 1. In the table, 1 indicates that the procedure is able to identify all the damaged bars independently from the level of damage. In presence of noise, 100 runs are performed for each case scenario. The number of successful damage identifications is collected in Tables 2, 3 and 4 for noise level equal to $1 \%$, $2 \%$ and $3 \%$, respectively. Overall, the performance of the identification is satisfactory for all the considered noise levels. As expected, poorer performance is attained for the lowest levels of damage ($5\%$ and $10\%$ reduction of modulus of elasticity).

Table 1. Identifications of the damaged bar in each damage scenario of the truss structure without noise.

Table 2. Identifications of the damaged bar in each damage scenario of the truss structure with noise equal to $1\%$.

Table 3. Identifications of the damaged bar in each damage scenario of the truss structure with noise equal to $2\%$.

Table 4. Identifications of the damaged bar in each damage scenario of the truss structure with noise equal to $3\%$.

3.2 Beam Structure

The simply-supported beam represented in Fig. 2 is used to validate the proposed method, [11]. The beam is a wide-flange W 12$\times$16 type, with modulus of elasticity $E=199.95$ GPa and material density $\rho =7837.1$ kg/m$^{3}$, respectively. The beam is divided into $n_e = 16$ elements and the first $m=7$ mode shapes and frequencies are employed to approximate the flexibility matrix. As for the truss case, four noise levels, which pollute the mode shape components are considered: no noise, $1\%$, $2\%$ and $3\%$. Damages are applied to each element e, in turn, with five increasing levels of damage d: $10\%$, $30\%$, $50\%$, $70\%$ and $90\%$.

In absence of noise, all the elements are identified. When $1\%$ noise is added, all the identifications in Table 5 are successful, with an identification rate higher than $50 \%$. As expected, for higher levels of noise ($2 \%$ and $3 \%$ in Tables 6 and 7, respectively), the identification rate decreases, even if the main issues remain connected to the lower level of damage, equal to $10\%$ of elastic modulus reduction and not relevant for a possible structural failure.

It should be noted that all the components of the mode shapes are required in order to build the flexibility matrix. However, in onsite campaigns this condition is not feasible, in fact data related to the rotational degrees of freedom of a beam are difficult to measure. The present approach can be easily modified to take into account incomplete mode shape components that can be expanded by means of common techniques of dynamic condensation available in literature, see for example [14,15,16].

Fig. 2.

Simply-supported beam under study. Measures in meters.

Table 5. Identifications of the damaged elements in each damage scenario of the beam structure with noise equal to $1\%$.

Table 6. Identifications of the damaged elements in each damage scenario of the beam structure with noise equal to $2\%$.

Table 7. Identifications of the damaged elements in each damage scenario of the beam structure with noise equal to $3\%$.

4 Conclusions

In this paper, an approach for localization of damage in truss and beam structures by using the flexibility matrix was presented. The flexibility matrix was approximated considering the first frequencies and mode shapes of the structures as obtained from experimental measures. The damage detection of a one-span truss and a simply supported beam was performed calculating modal strain and modal curvature changes to identify the damaged element. Results demonstrated the efficiency of the proposed method for dealing with single damage cases considering different damage extents and increasing levels of noise. The procedure can be easily extended to account for multiple damaged elements and incomplete mode shape data.