Shear Capacity Model with Variable Orientation of Concrete Stress Field for RC Beams Strengthened by FRP/FRCM

Abstract

A design-oriented analytical model able to evaluate the shear capacity of RC beams strengthened with FRP/FRCM sheets or strips oriented in any direction is proposed. The formulation of the model is based on the variable-inclination stress-field approach, aiming to extend the Eurocode 2 framework to beams strengthened in shear using FRP/FRCM. Complete, U-shaped and two-side wrapping schemes are considered. The influences of both steel and fiber composite transverse reinforcements on the orientation of the compressive concrete stress field in the web are taken into account. Interaction between steel and fiber transversal reinforcement is considered, adopting equations able to limit their global efficiencies. Effectiveness of the proposed model adopting different relations for the assessment of the effective composite and steel strains provided by international codes is investigated. Shear capacity values predicted by the model and those obtained using international codes are compared against experimental results proving the efficiency of the proposed model.

1 Introduction

The use of composite textiles such as Fibre Reinforced Polymer (FRP) or Fibre Reinforced Cementitious Matrix (FRCM) is gaining in popularity in the retrofitting of Reinforced Concrete (RC) structures. Reliable models have been developed for the flexural strengthening of RC members by using these composite textiles. The development of models able to assess the shear resistance of strengthened RC members is hindered by the difficulty to predict accurately the position and the shape of the failure surface, which is affected by several parameters (e.g. size effect, aggregate interlock, dowel effect, depth to span ratio, and efficiency of the composite reinforcement). International codes (e.g. ACI 440.2–17 (2017), ACI 549.4R-13 (2013), CAN/CSAS6–06 (2006), CNR-DT-200 (2004), Fib Task Group 9.3 (2001)) assessed the shear resistance of RC beams strengthened by using FRP or FRCM via an additive approach, namely the nominal shear resistance V_n is obtained by summing the contribution provided by the concrete V_c, the stirrups V_s and the composite textiles V_f. More recently, CNR-DT-200/R1 (2013) and CNR-DT-215 (2018) evaluate the shear resistance of strengthened RC members employing the variable inclination truss mechanism, in order to be consistent with the model used by Eurocode 2 and NTC 2018. However, in both the two former codes, it is not clear how, in the presence of reinforcing fiber and existing steel reinforcement oriented with different slopes, the shear strength ensured by the compressed concrete strut V_Rc must be evaluated when stirrup and fiber lie in two different direction. Within this framework, the aim of the present paper is to propose a new model able to assess the shear resistance of RC beams strengthened in shear by means of composite textiles (i.e. FRP or FRCM) arranged in any direction. The model is based on the theory of the stress fields with variable inclinations and is developed to compute the shear capacity of RC beams strengthened using two orders of reinforcement arranged in two different directions. The main advantages of the proposed model are: - solve the aforementioned drawback in the evaluation of V_Rc, being consistent with the shear resistance model used by Eurocode 2 and NTC 2018; - proposing an equation to calculate the slope of the concrete compressive stress field. Moreover, in order to increases the accuracy of the model suggested by the codes, a strategy to compute an equivalent angle of the transverse reinforcement involved in the calculation of the shear strength ensured by the compressed concrete V_Rc is proposed. It takes into account the amount of both the pre-existent steel stirrup and added reinforcing fiber. Two databases for FRP and FRCM elements have been used to assess the model efficiency. The comparison between the shear capacity predictions by the proposed models against those provided by international codes and proposed in literature models proves the model reliability.

2 Proposed Model

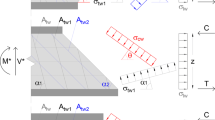
Colajanni et al. (2017) proposed a model, based on the stress field approach, able to assess the shear strength of RC members strengthened by FRP considering the interaction between bending moment, shear and axial forces. However, the model, even if it is reliable in the shear capacity prediction, is affected by some limitations. Namely the direction of the composite textile has to be perpendicular to the axis of the RC member, and the shear capacity is obtained by using an iterative numerical procedure. In this context, a simplified, reliable, straightforward, and design-oriented model is proposed here. It is based on the analytical model in Colajanni et al. (2020), able to calculate the shear capacity of RC beams reinforced with two orders of differently oriented transverse steel stirrups. This model is here adapted to RC beams having a single order of stirrups and strengthened in shear by composite textile by means of the same procedure used for the 2017 model. In particular, according to the 2020 model, the vertical equilibrium of beam segments obtained via three different sections parallel to the web concrete or reinforcing stress field can be written as follows:

$$ \begin{gathered} v = \tilde{\sigma }_{tw1} \omega_{tw1} \left( {\cot \theta + \cot \alpha_1 } \right)\sin^2 \alpha_1 + \hfill \\ \,\,\,\,\,\,\, + \tilde{\sigma }_{tw2} \omega_{tw2} \left( {\cot \theta + \cot \alpha_2 } \right)\sin^2 \alpha_2 \hfill \\ \end{gathered} $$

(1)

$$ \begin{gathered} v = \tilde{\sigma }_{cw} \left( {\cot \theta + \cot \alpha_j } \right)\sin^2 \theta + \hfill \\ \,\,\,\,\,\,\, + \tilde{\sigma }_{twi} \omega_{twi} \left( {\cot \alpha_i - \cot \alpha_j } \right)\sin^2 \alpha_i \,\, \hfill \\ \end{gathered} $$

(2,3)

where in Eq. (2) i = 1 and j = 2, and in Eq. (3) i = 2, j = 1. In the above equations v is the shear resistance made non-dimensional with respect to b_w z f’_cd (z = section effective depth), $\omega$_tw1 and $\omega$_tw2, the mechanical ratios of the two orders of reinforcement arranged in the two different directions $\alpha$₁ and $\alpha$₂ with respect to the beam axis, respectively, and $\overline{\sigma }$_tw1 and $\overline{\sigma }$_tw2 the correspondingly stresses made non-dimensional by using the design strength of steel f_yd. The shear capacity of a RC beam is computed via the static theorem of theory of plasticity, which gives an assessment of the shear resistance as the maximum value among the possible solutions satisfying both the equilibrium condition (1)-(3) and the following inequalities of plastic admissibility:

$$ 0 \le \tilde{\sigma }_{cw} , \left| {\tilde{\sigma }_{tw1} } \right|,\left| {\tilde{\sigma }_{tw2} } \right| \le 1 $$

(4)

The plastic admissible condition is obtained by combining (1) and (2), as follows:

$$ \begin{gathered} 0 \le \tilde{\sigma }_{cw} = (\tilde{\sigma }_{tw1} \omega_{tw1} \sin^2 \alpha_1 + \hfill \\ \,\,\,\,\,\,\,\,\, + \tilde{\sigma }_{tw2} \omega_{tw2} \sin^2 \alpha_2 )\left( {1 + \cot^2 \theta } \right) \le 1 \hfill \\ \end{gathered} $$

(5)

The above inequalities clarify the relation between the stress fields of both the web concrete and the two orders of transverse reinforcement. Moreover, according to Eurocode 2, the slope of the concrete stress field is limited in the range 1 < cot $\theta$ < 2.5. Therefore, in order to adapt Eq. (1) to the case of RC beam strengthened in shear by using composite textiles, the contribution of the first order of stirrups inclined by $\alpha$₁ is substituted with that provided by the fiber strengthening system. Furthermore, a reduction factor affecting the stirrups is added, in order to take into account that the brittle behaviour at failure of the composite textiles hinders the attainment of the yield strength in all the stirrups involved by the critical crack. This reduction factor, named r, depends on the ultimate strain of the transverse reinforcement. Thus, Eqs. (1)-(3) can be rewritten as follows:

$$ \begin{gathered} v = R \widetilde{\sigma }_{fw} \omega_{fw} \left( {\cot \theta + \cot \alpha_1 } \right)\sin^2 \alpha_1 + \hfill \\ \,\,\,\,\,\,\,\, + r\,\widetilde{\sigma }_{sw} \omega_{sw} \left( {\cot \theta + \cot \alpha_2 } \right)\sin^2 \alpha_2 \hfill \\ \end{gathered} $$

(6)

$$ \begin{gathered} v = \tilde{\sigma }_{cw} \left( {\cot \theta + \cot \alpha_2 } \right)\sin^2 \theta + \hfill \\ \,\,\,\,\,\,\, + R\,\tilde{\sigma }_{fw} \omega_{fw} \left( {\cot \alpha_1 - \cot \alpha_2 } \right)\sin^2 \alpha_1 \,\, \hfill \\ \end{gathered} $$

(7)

$$ \begin{gathered} v = \tilde{\sigma }_{cw} \left( {\cot \theta + \cot \alpha_1 } \right)\sin^2 \theta + \hfill \\ \,\,\,\,\,\,\, + r\,\tilde{\sigma }_{sw} \omega_{sw} \left( {\cot \alpha_2 - \cot \alpha_1 } \right)\sin^2 \alpha_2 \,\, \hfill \\ \end{gathered} $$

(8)

where $\overline{\sigma }$_fw, $\overline{\sigma }$_sw, $\omega$_fw, and $\omega$_sw are the non-dimensional stresses and the mechanical ratios of the composite shear strengthening and stirrups respectively:

$$ \widetilde{\sigma }_{fw} = \sigma_{fw} /f_{fu} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\widetilde{\sigma }_{sw} = \sigma_{sw} /f_{swy} $$

(9)

$$ \begin{gathered} \omega_{fw} = \left( {A_{fw} f_{fu} } \right)/\left( {b_w s\sin \alpha_1 f_{cm}^{\prime} } \right) \hfill \\ \omega_{sw} = \left( {A_{sw} f_{ym} } \right)/\left( {b_w s\sin \alpha_2 f_{cm}^{\prime} } \right) \hfill \\ \end{gathered} $$

(10)

where f_fu is the nominal rupture stress of the fibre, R the strain and stress “effective” coefficient (effective strain $\varepsilon$_fe=$\varepsilon$_fu R, effective stress f_fe=f_fu R=E_f $\varepsilon$_fe), r is the reduction factor of the efficiency of the stirrups that take into account both that the strain of the most elongated stirrup at beam failure can be limited by the effective strain of the fiber, and that not all the stirrup along the critical crack are able to reaches that strain; r=0.5 if $\varepsilon$_fe ≤ $\varepsilon$_swy, or r=1–0.5 ($\varepsilon$_swy/$\varepsilon$_fe) if $\varepsilon$_fe > $\varepsilon$_swy is assumed.

The inequalities regarding the plastic admissible conditions are modified accordingly, as follows:

$$ 0 \le {\sigma }_{cw} ,{\,\sigma }_{fw} \le 1\,\,\,\,\,\,\,\,\,\,\, - 1 \le {\sigma }_{sw} \, \le 1 $$

(11)

In this paper, it is considered only the case of major practical interest, namely $\alpha$₁ and $\alpha$₂ ≤ 90°. Hence, Eq. (6), Eq. (8), and Eq. (11) are combined in the following form:

$$ \begin{gathered} 0 \le \tilde{\sigma }_{cw} = (R\,\tilde{\sigma }_{fw} \omega_{fw} \sin^2 \alpha_1 + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \,\tilde{\sigma }_{sw} \omega_{sw} \sin^2 \alpha_2 )(1 + \cot^2 \theta ) \le 1 \hfill \\ \end{gathered} $$

(12)

According to Colajanni et al. (2020), initially it is assumed that, at the failure, the stress limit is reached simultaneously in the three stress fields (i.e. $\tilde{\sigma }_{cw} = \tilde{\sigma }_{fw} = \tilde{\sigma }_{sw} = 1$). Therefore, rearranging Eq. (12) the equation able to calculate the inclination of the web concrete stress field can be obtained as follows:

$$ \cot \theta = \sqrt {{\left( \begin{gathered} R\,\,\omega_{fw} \sin^2 \alpha_1 + \hfill \\ r\, \widetilde{f}_{swe} \omega_{sw} \sin^2 \alpha_2 \hfill \\ \end{gathered} \right)^{ - 1} - 1}} $$

(13)

Based on the results of the above equation, assuming cot $\theta$_lim = 2.5, three cases are defined:

• 1 ≤ cot $\theta$ ≤ 2.5: shear resistance can be calculated using Eq. (6);

• cot $\theta$ > 2.5: in this case the amount of shear strengthening and stirrups is not sufficient to induce the attainement of the maximum resistance in the web concrete stress field. Thus, cot $\theta$ = 2.5 is assumed, and the shear capacity is computed through Eq. (6), assuming $\tilde{\sigma }_{fw} = \tilde{\sigma }_{sw} = 1$. . The stress value in the web concrete field can be calculated by using Eq. (12), in which cot $\theta$ = 2.5;

• cot $\theta$ < 1: in this case the shear failure is due to the attainment of the stress limit in the web concrete stress field and in one of the two shear reinforcement. Therefore, the other shear reinforcement is in the elastic range at the beam failure. Now, it is assumed that $\alpha$₁ < $\alpha$₂. With the aim of determining if the maximum shear is given by Eq. (7) with the composite textile reaching the effective strain in tension ($\tilde{\sigma }$_fw = 1) or (unlikely event) by Eq. (8) with the stirrups yielding in compression ($\tilde{\sigma }$_sw = -1), the following inequality is employed:

  $$ R\omega_{fw} \sin^2 \alpha_1 \le 0.5 + r\,\,\omega_{sw} \sin^2 \alpha_2 $$

  (14)

If the inequality is true, thus the composite textile attains its stress limit, and the stress acting on the stirrups is computed as follows:

$$ \tilde{\sigma }_{sw} = \left( {0.5 - R\,\omega_{fw} \sin^2 \alpha_1 } \right)/\left( {r\,\omega_{sw} \sin^2 \alpha_2 } \right) $$

(15)

Conversely, if the inequality is false, thus the stirrups yield in compression, and the stress acting on the composite textile is calculated as follows:

$$ \tilde{\sigma }_{sw} = \left( {0.5 + r\,\omega_{sw} \sin^2 \alpha_2 } \right)/\left( {\,R\,\omega_{fw} \sin^2 \alpha_1 } \right) $$

(16)

3 Efficiency Coefficient R

3.1 FRP

The efficiency coefficient R is applied to the nominal ultimate strain of the fibres and depends on three different failure modes (Smith & Teng 2002): 1) failure of the FRP; 2) debonding at the FRP-concrete interface; 3) excessive width of the shear cracks. In Pellegrino & Modena (2006) a fourth failure mode has been detected, namely the separation of the concrete cover along a vertical plane (peeling off). At last, the efficiency coefficient R, R_i being the ratios between the FRP strain $\varepsilon$_fe at the attainment of each of the above mechanism and the nominal ultimate strain $\varepsilon$_fu, can be computed as follows:

$$ R = min\left\{ {R_1 ,R_2 ,R_3 ,R_4 } \right\} $$

(17)

Over the last two decades, several formulations have been developed in order to obtain the above coefficients. In the proposed model, the following equations are selected to describe the four modes of failure. The efficiency coefficient R₁, which takes into account the tensile failure of the FRP, is computed by means of the following equation proposed by Khalifa & Nanni (2000, 2002):

$$ R_1 = 0.56\left( {\rho_{fw} E_f } \right)^2 - 1.22\left( {\rho_{fw} E_f } \right) + 0.78 $$

(18)

where $\rho$_fw is the geometrical ratio of the composite textile and E_f the elastic modulus of the fibres. The coefficient R₂, representing the debonding phenomenon, is calculated using the following equation:

$$ R_2 = \frac{{\left( {f_{ck} } \right)^\frac{2}{3} \left( {d_{ft} - \eta L_e } \right)\left[ {738.93 - 4.06\left( {E_f t_f } \right)} \right]}}{{\varepsilon_{fu} d_{ft} 10^6 }} $$

(19)

where L_e is the effective length, which is evaluated using the expression provided by ACI and CSA:

$$ L_e = 23300/\left( {E_f t_f } \right)^{0.58} $$

(20)

$\eta$ is a parameter that takes into account the anchorage conditions, and it is equal to 1 or 2 if the shear strengthening is U-shaped or side-only, respectively. The range of validity of Eq. (20) is 20 ≤ E_f t_f ≤ 90. In case of complete wrapping or U-shaped strengthening with anchorages able to prevent debonding effect, the coefficient R₂ is not taken into account. Regarding the coefficient R₃, the following equation proposed by Khalifa & Nanni (2000) has been selected:

$$ R_3 = 6 \cdot 10^{ - 3} /\varepsilon_{fu} $$

(21)

In case of side-bonding and U-jacketing reinforcement, the FRP failure often involves the separation of the concrete cover along a vertical plane (peeling off). Hence, the coefficient proposed by Pellegrino & Modena (2006) is assumed equal to:

$$ R_4 = \frac{{2f_{ct} A_c \cos^2 \beta b_{c,v} }}{{n_f t_f L_f E_f \left[ {\left( {h_f - L_e } \right)/\left( {h_f } \right)} \right]b_f \varepsilon_{fu} }} $$

(22)

Further details about the parameters involved by Eq. (22) can be found in the above mentioned paper.

The model derived for FRP will be extended to evaluate the shear resistance of beam strengthened with FRCM. In order to assess through which efficiency coefficient the proposed model provides the best results, a comparison by using several efficiency coefficients applied to the proposed model is carried out. To this aim, the efficiency coefficients reported in ACI 549.4R-13, Triantafillou & Papanicolau (2006) (TRT06), Ombres (2015), Tetta et al. (2018) (TRT18) are employed. For the sake of brevity, the details of the coefficients are not reported here and can be found in the above-mentioned references.

4 Investigated Code Models

4.1 FRP

The models suggested by CNR and ACI are used to compare the efficiency of the proposed model. To this aim, it is noteworthy that the equation proposed by CNR-DT-200 R1/2013 to calculate the shear strength of RC beams strengthened by FRP is formulated in order to be a direct extension of the equation reported in Eurocode 2 to assess the shear strength of RC members. As a matter of fact, the shear resistance can be computed in non-dimensional form as follows:

$$ \begin{gathered} v_s = \omega_{sw} \left( {\cot \theta + \cot \alpha } \right)\sin^2 \alpha \hfill \\ v_f = \omega_{fw} \left( {\cot \theta + \cot \beta } \right)\sin^2 \beta \hfill \\ v_c = \left( {\cot \theta + \cot \psi } \right)/\left( {1 + \cot^2 \theta } \right) \hfill \\ \end{gathered} $$

(23)

$$ v = \min \left( {v_s + v_f ,v_c } \right) $$

(24)

where $\omega$_sw and $\omega$_fw are computed substituting f_fu with the design value f_fed. Appendix G of the above-mentioned code suggests to use cot $\theta$ = 1. Moreover, the third of Eq. (23) takes into account the inclination of only one of the two shear reinforcements by means of angle $\psi$. Thus the code suggests to consider the angle of arrangement of FRP strips $\beta$, neglecting any considerations about the amount of each shear reinforcement. On the basis of these considerations, two different ways to use the equation of the shear capacity reported by CNR code are here proposed:

• first method (CNR1): the slope of the web concrete stress field is computed in order to maximize the shear strength. Thus, by equating the third of (23) with the sum of the first and the second of (23), the following cubic equation is obtained:

$$ \begin{gathered} \cot^3 \theta [\omega_{sw} sen^2 \alpha + \omega_{fw} sen^2 \beta ] \, + \hfill \\ + \cot^2 \theta [\omega_{sw} sen^2 \alpha cot\alpha + \omega_{fw} sen^2 \beta cot\beta ] \, + \hfill \\ + \cot \theta [\omega_{sw} sen^2 \alpha + \omega_{fw} sen^2 \beta - 1] = \hfill \\ = cot\psi - \omega_{sw} sen^2 \alpha cot\alpha - \omega_{fw} sen^2 \beta cot\beta \hfill \\ \end{gathered} $$

(25)

Angle $\psi$ is set equal to $\beta$, consistently with the Appendix G of the CNR code;

• - Second method (CNR2): the angle $\psi$ is calculated proposing a simple procedure with takes into account the mechanical ratio of each of the two shear reinforcements, as follows:

• 1) A tentative value of cot $\theta$, cot $\theta$* = 1.75, is assumed to be the middle of the range of variation reported in the code, namely 1 ≤ cot $\theta$ ≤ 2.5;

• 2) Shear capacity values provided by FRP reinforcement and stirrups are calculated by using the first and the second of (23), i.e. v’_s and v’_f; are used to compute a weighted $\psi$’ angle as follows:

  $$ \psi^{\prime} = (v_s^{\prime} \cdot \alpha + v_f^{\prime} \cdot \beta )/\left( {v_s^{\prime} + v_f^{\prime} } \right) $$

  (26)

Angle $\psi$’ value calculated with Eq. (26) is used to obtain a new cot $\theta$ value, named cot $\theta$’, by means of Eq. (25).

The above procedure can be iteratively employed until the difference between two successive iterations is negligible. However, numerical evaluations carried out using this procedure have shown that one iteration is able to provide a reliable values of cot $\theta$. Regarding the shear resistance assessment, three cases are defined both for CNR1 and CNR2:

As for the ACI model, for brevity no equations are reported, being the model applied without any interpretation.

4.2 FRCM

The models selected to carry out the comparison are proposed by: ACI 549.4R-13, Triantafillou & Papanicolau 2006 (TRT06), Ombres 2015, Tetta et al. 2018 (TRT18). Excepting the ACI model, the other ones provide only the equations to calculate the shear contribution due to the FRCM reinforcement. Therefore, the efficiency of the models is evaluated by comparing the shear resistance provided by the FRCM reinforcement only.

5 Numerical Analysis

5.1 FRP

With the aim of comparing the efficiency of the above described model, a database containing 148 specimens of RC beams having rectangular or T-shaped cross-section, strengthened in shear by means of FRP strips or sheets has been collected. The specimens are reported in the following papers: Uji (1992), Al-Sulaimani et al. (1994), Chajes et al. (1995), Sato et al. (1997), Chaallal et al. (1998), Khalifa & Nanni (2000), Deniaud & Cheng (2001), Khalifa & Nanni (2002), Pellegrino & Modena (2002), Dost (2003), Taljsten (2003), Adhikary & Mutsuyoshi (2004), Carolin & Taljsten (2005), Bousselham & Chaallal (2006), Pellegrino & Modena (2006), Leung et al. (2007), Monti & Liotta (2007), Pellegrino & Modena (2008), Grande et al. (2009), Sundarraja & Rajamohan (2009), Belarbi et al. (2011), Katakalos et al. (2012), Panda et al. (2013), Baggio et al. (2014), Colalillo & Sheikh (2014). The database contains beams strengthened by using side-bonding, U-jacketing or complete wrapping schemes. Moreover, carbon, glass or aramid fibres are used in the specimens. The effective depth of cross-section of beams ranges between 150 and 940 mm, while the shear span is comprised between 2.50 and 4.00. Transverse reinforcement, if any, is constituted by vertical stirrups whose maximum geometrical ratio is equal to 0.75%. As regards FRP reinforcement, the ultimate tensile strength ranges between 106 and 4500 MPa, while the elastic modulus is comprised between 11 and 392 GPa. Lastly, the FRP geometrical ratio ranges between 0.06% and 4.00%. For the sake of brevity, the details of the investigated specimens are not reported here.

The shear resistance evaluation is carried out using the proposed model, the ACI model, and the model developed by CNR in the above-described forms, namely CNR1 and CNR2. It should be stressed that the 2013 version of the CNR model does not allow the side-bonding configuration. So, in case of specimens with this type of shear reinforcement, the 2004 version of the CNR model is employed. In Fig. 1 the results of the ratio between the experimental strength and the numerical prediction of the shear capacity for each specimen of the database and for each model are illustrated.

Fig. 1.

Experimental results vs. numerical predictions of the four investigated methods: CNR1, CNR2, ACI and the proposed model

From the above figure, it can be stated that CNR1, CNR2 and the proposed model provide average values near the unity, while that obtained by.

ACI is almost equal to 1.3. As for the Coefficient of Variation (CoV), all the models provide values equal to or greater than 0.3, highlighting their imperfections in managing such a large database. Therefore, the results are divided in subgroups: 1) side-bonding; 2) U-jacketing and complete wrapping, reported in Fig. 2, both with or without stirrups.

As for the side-bonding scheme, the results provided by the CNR 2004 model well reproduce the experimental values, with average values almost equal to 1 and CoV of 0.22. On the contrary, the proposed model provides a conservative response, with average value of 1.07, but with a much higher CoV, equal to 0.35. Average and CoV values obtained via ACI model are 1.19, and 0.31, respectively. It must be underlined that the 2004 version of the CNR model is not affected by the $\psi$ angle, thus CNR1 and CNR2 models provide the same results. From the analysis of the results reported in Fig. 2, it can be observed that the model which provides both the best average and CoV, 1.04 and 0.32 respectively, is the proposed model. Despite the same average value, CNR1 model provides a higher CoV, equal to 0.35. Moreover, CNR2 model provides results which are almost equal to those obtained through CNR1 one. Lastly, ACI model seems very conservative, with an average value of 1.33 and a CoV equal to 0.29. By comparing the results of the groups of beams with stirrups, the proposed model provides the best values in terms of average and CoV, equal to 1.01 and 0.25 respectively. Results obtained via CNR2 model are slightly better than those provided by CNR1 one, proving the efficiency of the proposed procedure to calculate the value of the angle $\psi$. Conservative results are provided by ACI model, with average and CoV values equal to 1.25 and 0.3 respectively. In case of beams without stirrups, the results are controversial. As a matter of fact, the proposed model provides the best average value and the worst CoV value, 1.09 and 0.43, respectively. CNR1 and CNR2 models have average and CoV values equal to 1.29 and 0.37. Lastly, ACI model provides the worst average and the best CoV values, equal to 1.54 and 0.24, respectively.

Fig. 2.

Experimental results vs. numerical predictions for beams reinforced with U-jacketing and complete wrapping schemes

Fig. 3.

Experimental results vs. numerical predictions for beams reinforced with U-jacketing and complete wrapping schemes and $\beta$ ≠ 90°

In order to highlight the advantages of the proposed model, a subgroup containing beams strengthened with U-jacketing and complete wrapping schemes with stirrups and fibres arranged with an angle $\beta$ ≠ 90° is analysed and the results are illustrated in Fig. 3. As it can be seen, the proposed model provides better results if compared to CNR1 model ones. In particular, if the average value is slightly nearer to one, from 0.8 to 0.85, the CoV value halves, from 0.35 to 0.17, confirming the effectiveness of the proposed model in reproducing the shear capacity of beams with the above-mentioned characteristics. Moreover, the results obtained by using the CNR2 model are slightly better than those provided by CNR1 one, highlighting the utility of the proposed procedure to compute the angle $\psi$. However, the best results are provided by the ACI model, with average and CoV values equal to 0.98 and 0.16, respectively.

5.2 FRCM

In order to assess the performances of the above-mentioned models, a database containing 139 specimens of RC beams reinforced in shear by using FRCM has been gathered. The specimens are reported in the following papers: Gonzalez-Libreros et al. (2017.a), Younis et al. (2017), Gonzalez-Libreros et al. (2017.b); Younis & Ebead (2018), Tetta et al. (2018), Marcinczak & Trapko (2018, 2019); Marcinczak et al. (2019). The database contains beams with rectangular or T-shaped cross-section, having effective depth between 159 and 419 mm, while the shear span is comprised between 1.6 and 4.9. Transverse reinforcement, if any, is constituted by vertical stirrups with maximum geometrical ratio of 0.5%. With regards to the FRCM, values of the parameters are different if related to the dry fibres or to the composite. The former are characterized by ranges of ultimate tensile strength f_fu, elastic modulus E_f, and geometrical ratio of reinforcement $\rho$ _f equal to 574 – 5800 MPa, 32 – 270 GPa, 0.02% and – 0.7%. Respectively. The latter, which are not provided for each specimen, are in the following ranges: ultimate tensile strength f_u,composite between 767 and 2253 MPa, elastic modulus E_composite between 41 and 168 GPa. The database contains beams strengthened by using side-bonding, U-jacketing or complete wrapping schemes. The fibres are made of carbon (C), PBO, basalt (B), glass (G) and high-performance steel (UHTSS). It should be underlined that not all the beams contained in the database can be used to assess the efficiency of the ACI model.

In Fig. 4 the results of the ratio between the experimental value and the numerical prediction of the shear capacity of the four models are showed.

Generally speaking, none of the models here analysed provide excellent results. As a matter of fact, all the models provide high CoV values, ranging from 0.59 of TRT18 to 0.95 of TRT06. These models are also those whose average values are closer to 1. Results provided by the Ombres model are quite conservative, with an average value of 1.36, while the CoV value is similar to that of the other models, equal to 0.70. As for the ACI model, the average value is equal to 2.59, while the CoV value is similar to the TRT18 one, equal to 0.64. It must be stressed that the results given by the ACI model could have been affected by the limited database employed.

Regarding to the proposed model, the efficiency coefficients of the four models are applied to the proposed model in order to evaluate which is the one that provides the best results. This comparison is reported in Fig. 5.

The results obtained via the proposed model imitates the above-described ones. Indeed, the best values in terms of average and CoV are given by using the efficiency coefficient employed by the TRT18 model, namely 1.14 and 0.65, respectively. Conservative behaviour is registered employing the efficiency coefficient of ACI and Ombres, with average values equal to 1.86 and 2.46, respectively.

Fig. 4.

Shear resistance provided by the FRCM reinforcement vs. numerical predictions of the four investigated methods: TRT06, ACI, Ombres and TRT18

Fig. 5.

Experimental results vs. numerical predictions of the proposed model employing the efficiency coefficients of the four investigated methods

6 Conclusions

A model able to assess the shear capacity of RC beams strengthened in shear by means of composite textiles (FRP/FRCM) arranged both in the same or different direction of the pre-existing stirrup has been proposed. The model is based on the theory of the stress fields with variable inclination, and is developed in order to be a direct extension of the truss mechanism employed by Eurocode 2 and NTC 2018 to evaluate the shear capacity of RC members. To this aim, the model rearranges the equation proposed in Colajanni et al. (2020) to compute the slope of the web concrete stress field, taking into account the shear strengthening. In order to assess the model efficiency, two databases (one for FRP and one for FRCM) have been defined and the experimental results to numerical provisions ratios of the proposed model have been compared to those obtained via several models (ACI 440.2R-17 (2017), CNR-DT 200 R1/2013 for FRP; ACI 549.4R-13, Triantafillou & Papanicolau 2006 (TRT06), Ombres 2015, Tetta et al. 2018 (TRT18) for FRCM). The results prove the superior reliability of the proposed model in predicting the shear strength of specimens reinforced with stirrups and inclined composite textiles, for which small CoV are obtained, while it is able to provide results at least equal to those obtained by using the above-mentioned models in all the other strengthening layout.