Keywords

1 Introduction

Severe damages and failures of existing reinforced concrete (RC) buildings observed during recent and past seismic events frequently involved exterior beam-column joints. Indeed, their configuration (unconfined joints) and deficiencies in terms of amount and details of steel reinforcement (lacks of stirrups and longitudinal steel bars without efficient anchorage ends) could make beam-column joints the weakest component of RC frames.

The literature contains a significant amount of studies concerning the experimental behavior of RC beam-column joints (De Risi et al. 2016, Realfonzo et al. 2014.

Other studies focus on the numerical modelling of the monotonic and cyclic response of RC beam-column joints (Alath and Kunnath 1995; Lowes and Altoontash 2003).

Nevertheless, the difficulties in reproducing the main phenomena affecting the monotonic and cyclic behavior of these elements and the importance of considering their role on the seismic response of existing buildings, make this topic of particular relevance and necessary to be further analysed.

Aim of this paper is to numerically simulate the monotonic and cyclic response of typical exterior beam–column joints without transverse reinforcements. To this purpose, constitutive laws obtained by combining some literature models are proposed. These are implemented into a simple model for beam-column joints where both the shear behavior and the possible occurrence of the slippage of longitudinal bars of beam from the joint are considered. The numerical analyses are carried out by using the open-source finite element platform OpenSees (McKenna et al. 2010).

The reliability of the obtained laws is assessed in the paper with reference to a set of seven experimental cases, representative of exterior joints without transverse reinforcements, collected from literature.

2 Shear Behavior of Exterior Joints: Literature Models

The experimental shear behavior of exterior beam–column joints can be described by the following main phenomena: a cracking process, the attainment of the peak strength, a subsequent process of strength degradation until the attainment of a residual shear strength value. This leads to adopt for its modelling a multi-linear shear stress-strain (τ-γ) constitutive law as that reported in Fig. 1. Then, the multi-linear law can be implemented into a macro-modelling approach available within the several commercial computer codes (McKenna et al. 2010) available nowadays, to perform numerical analyses.

Fig. 1.
figure 1

Multilinear stress-strain relationship.

Full size image

The multi-linear law is completely defined by four characteristic points in terms of stress (τ1, τ2, τ3, τ4) and strains (γ1, γ2, γ3, γ4).

In particular, regarding the evaluation of the shear strength τ3, (in the following indicated as τmax) the following five models available in the literature are considered in the present paper.

The first model (Model 1), proposed by Kim and LaFave (2008), provides the following expression:

$$ \tau_{\max } = \alpha_t \beta_t \eta_t \lambda_t {(JI)}^{0.15} {(BI)}^{0.3} {(f_c )}^{0.75} $$
(1)

where: αt is a coefficient depending on the joint configuration; βt is a coefficient dependent on the level of the exterior joint’s confinement; ηt is a coefficient related to the beam-column eccentricity; λt is a coefficient assumed equal to 1.31; fc is the concrete compressive strength; JI represents the “joint transverse reinforcement index”; BI is the “beam reinforcement index”.

The second model (Model 2) proposed by Vollum and Newman (1999), suggests the following expression:

$$ \tau_{\max } = 0.642\beta \left[ {1 + 0.555\left( {2 - \frac{h_b }{{h_c }}} \right)} \right]\sqrt {f_c } $$
(2)

where: β is a coefficient depending on the configuration of the beam’s longitudinal steel bar end inside the joint; hb is the beam height; hc is the column height.

The third model (Model 3), proposed by Ortiz (1993), provides:

$$ \tau_{\max } = \frac{\sigma_d b_c w_j \cos \theta }{{h_c b_c }} $$
(3)

where: σd is the design compressive concrete strength estimated according to the CEB-FIP Model Code 90 (1993); bc is the column width; bb is the beam width; wj is the strut width; θ is the angle between the strut and the longitudinal beam axis.

The fourth model (Model 4) is the one proposed by Hwang and Lee (1999) and suggests the following formula:

$$ \tau_{\max } = \frac{D\cos \theta + F_h + F_v \cot \theta }{{h_c b_c }} $$
(4)

where: D is the compressive strength of the concrete strut component; Fh and Fv are respectively the horizontal and the vertical components of the tie member strength.

The last model (Model 5) by Jeon (2013) gives:

$$ \tau_{\max } = 0.586{(TB)}^{0.774} {(BI)}^{0.495} {(JP)}^{1.25} {(f_c )}^{0.941} $$
(5)

where: TB coincides with the coefficient βt of Eq. (1); JP corresponds to the coefficient αt of Eq. (1).

A more detailed description of the five considered models can be found in Nitiffi et al. (2019).

Regarding the derivation of the other three values of the shear stresses (i.e. \(\tau_1\), \(\tau_2\), \(\tau_4\)) and of the four shear strains (i.e. \(\gamma_1\), \(\gamma_2\), \(\gamma_3\), \(\gamma_4\)), other models are considered in the present paper.

In particular, for the shear stress \(\tau_1\), the formula proposed by Uzumeri (1977) gives:

$$ \tau_1 = 0.29\sqrt {f_c } \sqrt {{1 + 0.29\frac{P}{A_j }}} $$
(6)

where P is the column axial load and Aj is the effective joint area.

For the other parameters, the values proposed by De Risi et al. (2016), Celik and Ellingwood (2008), Shin and LaFave (2004) and Sharma et al. (2011) are considered and summarized in Table 1. Model A indicates the model proposed by De Risi et al. (2016) and Model D that by Sharma et al. (2011); both these models propose a unique value for each of the above parameters. On the contrary the other two models propose a range of values for some of the parameters; Models B1-B2 indicate the model by Celik and Ellingwood (2008) evaluated respectively for the minimum and maximum values of the range, and Models C1-C2 indicate the one proposed by Shin and LaFave (2004) still at the minimum and maximum values of the ranges.

Table 1. Values derived from the accounted literature models
Full size table

All the above models are combined in order to reproduce the shear response τ-γ of the panel zone. In particular, the shear strength τ3 given by each of the Models 1, 2, 3, 4, 5 is combined with the other parameters given by Models A, B1, B2, C1, C2, D. A total of 30 τ-γ relationships are, hence, obtained and summarized in Table 2. These laws are implemented in the numerical analyses, describing the monotonic shear behavior of RC beam-column joints, and presented in the following.

Table 2. Schematization of constitutive laws derived by combining the literature models
Full size table

3 Numerical Analyses

The definition of accurate constitutive laws reproducing the shear behavior of RC beam-column joints is an important preliminary step for performing numerical analyses based on macro-modelling approaches.

3.1 The Macro-Modelling Approach for RC Beam-Column Joints

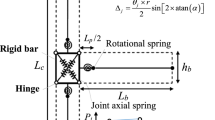
In this study, the so–called “scissors model”, proposed by Alath and Kunnath (1995), is used. This model is composed of a rotational spring connecting a master node and a duplicated slave node located at the same position in the middle of the panel zone. Moreover, these nodes are connected to the beam and column members through rigid links.

In order to account for the contribution of the fixed-end-rotation due to the slip phenomenon of the longitudinal bars of the beam, an additional nonlinear rotational spring is introduced at the interface between the panel zone and the adjacent beam (Fig. 2).

Fig. 2.
figure 2

Beam-column joint scissors model.

Full size image

The numerical analyses are carried out by using the open-source finite element platform OpenSees (McKenna et al. 2010) where both the rotational springs have been modelled by the “Pinching4 Uniaxial Material” with a multi-linear law in terms of moment-rotation (M-θ).

For what concern the joint shear spring, the (M-θ) law is defined with the rotation of the spring θj assumed equal to the joint panel strain γj and the bending moment Mj given by:

$$ M_j = \tau_j A\frac{1}{{\frac{{1 - {{h_c } / {2L_b }}}}{jd_b } - \frac{1}{2L_c }}} $$
(7)

where: τj is the shear stress of the multilinear law; A is the joint cross-section area; hc is the column height: Lb is the beam length; jdb is the beam internal lever arm; Lc is the column length.

Regarding the spring modelling the bond slip behavior of the joint panel, the (M-θ) law is that reported in Fig. 3 and defined as follows. Starting from the bond stress-slip relationship reported in Model Code (2010), (see Fig. 3) the maximum moment M3 is evaluated through the following formula:

$$ M = f_{stm,tr} A_s {jd}_b $$
(8)

where As is the longitudinal reinforcement area of the beam and fstm,tr is the maximum tensile stress developed in the bar and transferred by bond. The latter parameter can be evaluated according to the Fédération Internationale (2010) as follows:

$$ f_{stm,tr} = f_{stm} + 6\left( {\frac{l_b }{\phi }} \right)p_{tr} $$
(9a)

where lb and ∅ are the anchorage length of the longitudinal bar and its diameter, respectively, while fstm and ptr are given by:

$$ f_{stm} = 54{\left( {\frac{f_c }{{25}}} \right)}^{0.25} {\left( {\frac{l_b }{\phi }} \right)}^{0.55} {\left( {\frac{25}{\phi }} \right)}^{0.2} \left[ {{\left( {\frac{{c_{\min } }}{\phi }} \right)}^{0.25} {\left( {\frac{{c_{\max } }}{{c_{\min } }}} \right)}^{0.1} + k_m k_{tr} } \right] $$
(9b)
$$ p_{tr} = {N / {(b_c h_c )}} $$
(9c)

In Eqs. (9b) and (9c), cmin and cmax are geometrical parameters related to the concrete cover and the distance between adjacent bars respectively; km and ktr are parameters related to eventual transverse reinforcements, evaluated as suggested by the Fédération Internationale (2010); N is the axial load on the column which is normalized with respect to the member cross-section area.

According to the mentioned Code, the following relationship should be satisfied:

$$ f_{stm,tr} < 1.75f_{st,0} + 0.8\left( {\frac{l_b }{{p_{tr} }}} \right) < 8.0\left( {\frac{l_b }{\phi }} \right)f_c^{0.5} $$
(9d)

where: fst,0 is equal to fstm in the particular condition of cmin = ∅ and cmax/cmin = 1.

The moment M2 and M4, instead, are assumed respectively equal to 0.75M3 and 0.40M3, according to De Risi et al. (2016).

The rigid rotation θs of the joint panel due to the slip is obtained from the proposal by Otani and Sozen (1972) (Eq. 10), neglecting the slip of the bar in compression:

$$ \theta_s = \frac{slip}{{d - d^{\prime}}} $$
(10)

where (d-d′) is the distance between the longitudinal reinforcements in tension and compression.

In particular, the slip values are deduced from the Fédération Internationale (2010) in the case of pull-out failure: s2 is assumed equal to 1.8 mm, corresponding to the attainment of the bond strength; s3 is assumed equal to 3.6 mm, corresponding to the beginning of the bond strength degradation; s4 is assumed equal to 12 mm.

Fig. 3.
figure 3

Multilinear moment-rotation relationship for the bond-slip behavior.

Full size image

Finally, the value of M1 and the corresponding slip s1, have been directly obtained from the intersection of the first branch (corresponding to the rigid un-cracked phase) and the third branch of the adopted law. Indeed, since frame elements with a nonlinear behavior are considered in the modelling approach employed by the authors, the cracking effect is directly introduced at the beam section level.

The aim of the numerical analyses here presented is to assess the reliability of the obtained law in reproducing the monotonic experimental behavior of beam-column joints. Then, a set of specimens available in literature, representative of typical exterior RC beam – column joints and subjected to cyclic load histories have been considered.

In particular, the accounted set of experimental cases concerns the tests carried out by Realfonzo et al. (2014), Pantelides et al. (2002), Clyde et al. (2000), De Risi et al. (2016), Del Vecchio et al. (2014).

Table 3 summarizes the main informations on these case studies, where bb and hb are the width and the depth of the beam member, As,b is the beam longitudinal reinforcement area, whereas the other symbols were already defined earlier.

For each case, monotonic analyses have been performed by accounting for the 30 \(\tau - \gamma\) constitutive laws. The obtained results in terms of applied force vs. drift (the latter corresponding to the ratio between the displacement at the end of the beam and the beam length) are compared with the envelope of the experimental hysteretic cycles.

The relative error between the experimental and numerical forces is calculated up to the conventional value of 75% of the maximum experimental strength (both in the positive and negative direction of loading) through the following formula:

$$ Err = \frac{{\sum_{i = 1}^n {E_i } }}{n};E_i = \frac{{\left| {F_{\exp ,i} - F_{num,i} } \right|}}{{F_{\exp ,i} }}100 $$
(11)

where: Fexp,i and Fnum,i are the i-th experimental force and the corresponding numerical force respectively.

Table 3. Main geometric and mechanical properties of the experimental database.
Full size table
Table 4a. Mean absolute percentage errors [%] for the monotonic envelopes (positive branch)
Full size table
Table 4b. Mean absolute percentage errors [%] for the monotonic envelopes (negative branch)
Full size table

Tables 4a and 4b provide the percent error values for the positive branch and negative branch of the envelope curve, respectively. As noted, the models furnishing the lowest error vary among the accounted experimental tests. Indeed:

  • test J05: the lowest error values, equal to 9% and 6%, are provided by the model 5C1;

  • test J01: the lowest error values, equal to 15% and 14%, are provided by the model 1C1;

  • test TU3: the lowest error values, equal to 17% and 12%, are provided by the model 5A;

  • test TU1: the lowest error value, equal to 19%, is provided by the model 5A; in this case, the errors for the negative branch are related to the bond-slip mechanism and not accounted in this study;

  • test #4: the lowest error values equal, to 11% and 7%, are provided by the model 5A;

  • test T#1: the lowest error values, equal to 17% and 34%, are provided by the model 1A;

  • test T_C3: the lowest error values, equal to 15% and 14%, are provided by the model 4A.

It must be highlighted that the models B2 and C2 are not taken into account in the assessment of the percentage errors, due to relevant drift excursions for the current experimental case studies.

The comparison between the numerical curves and experimental monotonic envelopes considering the models furnishing the lowest error is shown in Figs. 4, 5 and 6.

It is possible to observe a good agreement between numerical and experimental results, even in terms of failure mode prediction; besides the joints affected by the shear failure of the panel zone, the anchorage failure of the specimen TU1 (Pantelides et al. 2002) is also captured.

Fig. 4.
figure 4

Comparison between numerical curves and experimental envelope: test J05 (a) and J01 (b) by Realfonzo et al. (2014).

Full size image
Fig. 5.
figure 5

Comparison between numerical curves and experimental envelope: test TU3 (a) and TU1 (b) by Pantelides et al. (2002).

Full size image
Fig. 6.
figure 6

Comparison between numerical curves and experimental envelope: specimens tested by (a) Clyde et al. (2000); (b) De Risi et al. (2016); (c) Del Vecchio et al. (2014).

Full size image

4 Assessment of the Joint Shear Strength

The monotonic simulations in Figs. 4, 5 and 6 highlight the strong correlation between the numerical evaluation of the global shear strength of joints and the correct estimate of the shear stress τmax Preliminary considerations are here carried out by comparing the values of τmax,num obtained from the analyzed Models 1 to 5 with the experimental value of shear strength (τmax,exp) obtained from the equilibrium of the forces acting on the joint panel:

$$ \tau_{\max ,\exp } = \frac{{T_b - V_{col} }}{A_j } $$
(12)

where Tb is the tensile force acting in the longitudinal bars of the beam, Vcol is the column shear force, Aj the cross-section area of the joint.

The scatter between the numerical and the experimental strength is calculated through the mean absolute percentage error as follows:

$$ Err = \frac{{\sum_{i = 1}^n {E_i } }}{n} = ;E_i = \frac{{\left| {\tau_{\max ,\exp ,i} - \tau_{\max ,num,i} } \right|}}{{\tau_{\max ,\exp ,i} }}100 $$
(13)

where τmax,exp,i and τmax,num,i are the i-th experimental and the i-th numerical shear strength, respectively.

The bar charts in Figs. 7a and b depict the errors for both the positive (“ +”) and negative (“-”) direction of loading in terms of the maximum shear strength estimated according to the considered five models. An exception is represented by the specimen TU1 (Pantelides et al. 2002) for which only the errors in the push (positive) direction were calculated since an anchorage failure due to loss of bond was experienced in the pull (negative) direction.

The bar chart in Fig. 8, instead, shows the mean error in the estimate of τmax computed by the models on all the considered tests and considering both the positive and negative directions together; the errors bars show the positive and negative deviation of the error from the mean value computed for each model.

From these graphs it can be noted that the accuracy of the all models is rather variable with the considered test. Overall, Model 1 (Kim and LaFave 2008) and Model 5 (Jeon 2013) seem to provide values of shear strength closer to the those emerged from experimental tests, since the mean errors amount to 13.6% and 14.6%, respectively (see Fig. 8).

Fig. 7.
figure 7

Model errors in terms of τmax by varying the considered experimental test: push direction (a); pull direction (b).

Full size image
Fig. 8.
figure 8

Model errors in terms of τmax on all the tests.

Full size image

5 Cyclic Response

The modelling of the cyclic behavior represents another key aspect in the study of the seismic response of the RC beam-column joints with a greater complexity with the respect to the monotonic behavior.

The constitutive laws obtained in the previous sections represent a valuable basis for carrying out cyclic analyses. Then, implementing the macro-modelling approach described in Sect. 2 and picking the laws providing the lowest value of the errors, cyclic analyses have been performed.

Regarding the shear behavior of the panel joint a calibration procedure has been done for the material model Pinching 4. To this purpose, for all the analyzed specimens, the parameters obtained from a calibration procedure carried out by Nitiffi et al. (2019) on the specimen J05 (Realfonzo et al. 2014) have been considered.

The results of these preliminary analyses in terms of cyclic behavior are compared with the experimental response in Fig. 9. The graphs show a general good agreement between experimental and numerical cyclic curves.

Fig. 9.
figure 9

Comparison between numerical and experimental cyclic curves: (a) test J01 by Realfonzo et al. (2014); (b) test #4 by Clyde et al. (2000); (c) test T#1 by De Risi et al. (2016); (d) test TC3 by Del Vecchio et al. (2014).

Full size image

6 Conclusions

In this study, a procedure has been presented for the calibration of constitutive laws to employ into numerical models for the study of the monotonic and cyclic response of beam-column joints. In particular, 30 laws have been obtained by opportunely combining some models available in literature.

The 30 laws have been implemented in a simple model where the behavior of joint is schematized throughout two rotational springs in series: one reproducing the shear behavior and the other the bond-slip behavior.

Numerical analyses, both monotonic and cyclic, have been then performed by selecting seven experimental cases from the literature. The monotonic analyses have allowed to identify the combinations of models which better simulate the experimental response of the specimens. Furthermore, the better laws have been subsequently used for performing preliminary cyclic analyses. The obtained results have underlined a good ability of the derived laws in reproducing both the monotonic and cyclic response of beam-column joints.

Further developments are needed to assess the proposed model for a wider experimental database, also including different joint configurations and structural details.