An Analytical Approach for Calculating Crack Width of RC Members: Pure Shear Method

Abstract

Nowadays Serviceability Limit State (SLS) of Reinforced Concrete (RC) structures is becoming a more and more important object of research among scientists and engineers. One of the most relevant topics of SLS is cracking due to its significant impact on the longevity and durability as well as aesthetic appearance of the structure. However, up until this day all theoretical models, dedicated to determining the most important characteristic of cracking behavior – crack width, are still highly debatable due to the high variation in the correspondence of the theoretical to experimental results. In this paper a new simple analytical approach for calculating average crack width of reinforced concrete members subjected to external short–term loading is presented. The new model is based on the concept of sole shear displacement occurring in the cover thickness of concrete due to the tangential stresses resulted by bonding. Theoretical crack width results obtained using the new approach are compared to the experimental results of tensile and bending members tested by different authors and the theoretical results of Eurocode 2 and Model Code 2010.

1 Introduction

Nowadays, due to gradual improvement of materials resulting in lighter and more slender structures, the Serviceability Limit State (SLS) becomes more and more relevant topic among scientists and engineers. When designing reinforced concrete (RC) structures, the most important design aspect, which is closely related to SLS, is cracking control. Excessively large cracks cause problems related to aesthetics and even induces a feeling of unsafety. Moreover, moisture or other chemical materials penetrating through cracks provoke the corrosion of reinforcement which in time results in the reduction of the structural durability. To avoid the above – mentioned issues, crack widths must be limited. To achieve this goal, it is important to have a model which, knowing certain structural configuration as well as certain environmental and loading conditions, could predict the expected width of the cracks forming on the surface of RC member. From the past century up until this day a wide variety of cracking models have been developed. However, due to high scatter of the correspondence to the experimental results their accuracy is still highly debatable.

Considering the necessity to develop a more accurate and simple cracking model, which would be capable of predicting one of the most important parameters of the SLS – crack width, in this paper a new simplistic analytical approach, which is based on the concept of sole elastic shear stains of concrete, is presented.

2 Assumptions and Derivation of Pure Shear Method

To obtain a simple analytical expression for practically evaluating mean crack width of RC members subjected to short–term loads, the following model is based on the simplified assumptions listed below:

• 1. All cracks are considered to be fully formed and no new additional cracks can form as a result of a subjected external load.

• 2. All materials are elastic.

• 3. Longitudinal axial strains occurring in concrete due to external loads are neglected.

• 4. Only shear strains which are assumed to be constant across the cover and range along the longitudinal axis of the member occur in concrete.

• 5. Perfect bond (no slip) between reinforcement and concrete is considered, resulting in distortion of the concrete sections as a result of occurring shear deformation (Fig. 1).

• 6. Only surface crack widths of RC member are considered.

• 7. Shrinkage is neglected.

• 8. The mean crack width is predicted.

Fig. 1.

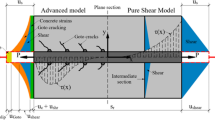
A singly reinforced concrete block representing the mean region between two adjacent cracks spaced at ${s}_{rm}$ (${d}_{b}$– bar diameter, $c$ – concrete cover, ${\gamma }_{c}$ – shear angle, ${u}_{s}$ – reinforcement displacement due to external loading, ${w}_{m}$ – mean crack width, $P$ – external short–term load)

Considering a tensile concrete block reinforced with a single reinforcing bar which is a representation of the average distance between two adjacent cracks (Fig. 1), and taking into account the assumptions 3–5, it can be stated that the axial displacement of the reinforcing bar at any point $x$ ($u_{s} (x$)) is equal to the shear displacement of concrete ($u_{shear} \left( x \right)$):

$$u_{s} \left( x \right) = u_{shear} \left( x \right).$$

(1)

Therefore, using the well–known classical expression (e.g., [1]) which describes a differential relationship between reinforcement strain and bonding stress:

$$\frac{{d\varepsilon_{s} \left( x \right)}}{dx} = \frac{4}{{E_{s} d_{b} }}\tau \left( x \right)$$

(2)

and considering that it is also mathematically true that the second derivative of reinforcement displacement ($u_{s} \left( x \right)$) is equal to the first derivative of reinforcement strain ($\varepsilon_{s} \left( x \right)$):

$$\frac{{d^{2} u_{s} \left( x \right)}}{{dx^{2} }} = \frac{{d\varepsilon_{s} \left( x \right)}}{dx},$$

(3)

a new expression can be written:

$$\frac{{d^{2} u_{s} \left( x \right)}}{{dx^{2} }} = \frac{4}{{E_{s} d_{b} }}\tau \left( x \right),$$

(4)

where $E_{s}$ is the elastic modulus of steel, $d_{b}$ is bar diameter and $\tau \left( x \right)$ is bonding stress between reinforcement and concrete. According to the assumption 4 and Fig. 1, it can be stated that the shear angle ($\gamma_{c} \left( x \right)$) is equal to the ratio of shear displacement ($u_{shear} \left( x \right)$) to the cover thickness of concrete ($c$):

$$\gamma_{c} \left( x \right) = \frac{{u_{shear} \left( x \right)}}{c}.$$

(5)

Taking into consideration the assumption 2 as well as the Eqs. (1) and (5):

$$\tau \left( x \right) = \gamma_{c} \left( x \right)G_{c} = \frac{{u_{shear} \left( x \right)}}{c}G_{c} = \frac{{u_{s} \left( x \right)}}{c}G_{c},$$

(6)

where $G_{c}$ is the shear modulus of concrete. From the Elastic Theory it is well known that:

$$G_{c} = \frac{{E_{c} }}{{2\left( {1 + \nu } \right)}},$$

(7)

where $E_{c}$ is the elastic modulus of concrete and $\nu$ is Poisson’s ratio (taken = 0.2 for uncracked concrete). Therefore, the Eq. (6) can be modified:

$$\tau \left( x \right) = \frac{{u_{s} \left( x \right)}}{c}\frac{{E_{c} }}{{2\left( {1 + \nu } \right)}}.$$

(8)

Then, according to Eqs. (4) and (8), the following expression can be written:

$$\frac{{d^{2} u_{s} \left( x \right)}}{{dx^{2} }} = \frac{{2E_{c} }}{{E_{s} d_{b} c\left( {1 + \nu } \right)}}u_{s} \left( x \right).$$

(9)

To simplify the form of Eq. (9) a new variable is introduced:

$${\text{K}} = \frac{{2E_{c} }}{{E_{s} d_{b} c\left( {1 + \nu } \right)}},$$

(10)

Rearranging the expression (9) results in a second order homogenous differential equation:

$$\frac{{d^{2} u_{s} \left( x \right)}}{{dx^{2} }} - {\text{K}}u_{s} \left( x \right) = 0.$$

(11)

The solution to the Eq. (11) has a general form:

$$u_{s} \left( x \right) = C_{1} e^{{x\sqrt {\text{K}} }} + C_{2} e^{{ - x\sqrt {\text{K}} }},$$

(12)

where $C_{1}$ and $C_{2}$ are the integration constants. To obtain the solution for a particular case shown in Fig. 1 the following boundary conditions, which take into consideration symmetry conditions and the reinforcement strain distribution, can be written:

$$u_{s} \left( 0 \right) = 0,\frac{{du_{s} }}{dx}\left( {\frac{{s_{rm} }}{2}} \right) = \varepsilon_{s} \left( {\frac{{s_{rm} }}{2}} \right) = \frac{P}{{E_{s} A_{s} }} = \varepsilon_{si},$$

(13)

where $\varepsilon_{si}$ is reinforcement strain considering fully cracked section. Furthermore, taking into consideration the Eq. (12) and (13) the integration constants $C_{1}$ and $C_{2}$ can be determined. This results in the function of reinforcement displacement at any point $x$:

$$u_{s} \left( x \right) = \frac{{\varepsilon_{si} }}{{\left( {1 + e^{{s_{rm} \sqrt {\text{K}} }} } \right)\sqrt {\text{K}} }}\left( {e^{{\left( {x + 0.5s_{rm} } \right)\sqrt {\text{K}} }} - e^{{\left( {0.5s_{rm} - x} \right)\sqrt {\text{K}} }} } \right).$$

(14)

Taking into consideration Eq. (1) and Fig. 1, an expression, relating the average crack width and the displacement of reinforcement at the end of RC block, can be written:

$$w_{m} = 2u_{s} \left( {0.5s_{rm} } \right).$$

(15)

Lastly, taking into consideration the expressions (14) and (15), a formula for calculating average crack width of a tensile member is derived:

$$w_{m} = \frac{{2\varepsilon_{si} }}{{\sqrt {\text{K}} }}\frac{{\left( {e^{{s_{rm} \sqrt {\text{K}} }} - 1} \right)}}{{\left( {e^{{s_{rm} \sqrt {\text{K}} }} + 1} \right)}}.$$

(16)

The only unknown in the Eq. (16) is the average crack spacing ($s_{rm}$). However, mathematically, the maximum possible value of the term $\frac{{\left( {e^{{s_{rm} \sqrt {\text{K}} }} - 1} \right)}}{{\left( {e^{{s_{rm} \sqrt {\text{K}} }} + 1} \right)}}$ is equal to 1. In this case, seeking conservative results, the Eq. (16) can be simplified:

$$w_{m} = \frac{{2\varepsilon_{si} }}{{\sqrt {\text{K}} }} = \frac{{2\sigma_{s} }}{{E_{s} \sqrt {\text{K}} }}$$

(17)

where $\sigma_{s}$ stress of reinforcement considering fully cracked section.

Equation (17) indicates that, similar to other theoretical models (e.g., [2,3,4]), the most important variable determining the crack width is reinforcement strain ($\varepsilon_{si}$). Other less important parameters are included in the variable ${\text{K}}$ (Eq. (10)) which are modulus of elasticity of both steel ($E_{s} )$ and concrete ($E_{c}$), bar diameter ($d_{b}$) and the cover thickness ($c$).

3 Verification of Model Using RC Ties and Beams

This section compares mean crack width (${w}_{m}$) predictions by the proposed model against the test data of RC ties and beams subjected to short–term loading reported in the literature. The comparison also includes the crack width models from Eurocode 2 (EC2) [5] and MC 2010 (MC2010) [6].

3.1 Analysis of RC Ties

The analysis employs 125 RC ties from 2 experimental programs reported by Wu and Gilbert [7] (4 members) and Farra and Jaccoud [8] (121 members). All the members were singly reinforced and basically having the same nominal geometry: a square section of 100 × 100 mm and length of 1100 or 1150 mm. Tension on RC ties was exerted by pulling them by the ends of reinforcement. Main geometrical and material parameters of the ties such as cylinder strength (${f}_{cm}$), modulus of elasticity of concrete (${E}_{c}$) and reinforcement (${E}_{s}$), bar diameter (${d}_{b}$), concrete cover ($c$), reinforcement ratio ($\rho$), and free shrinkage strain (${\varepsilon }_{cs}$) are presented in Table 1. It also should be noted that all the specimens were sorted by reinforcement ratio in ascending order.

Table 1. Main characteristics of test RC ties from the study of Wu and Gilbert [7] and Farra and Joccoud [8]

The accuracy of all 3 models – Eurocode 2 [5], Model Code 2010 [6] and Pure Shear Method (PSM) was judged by two parameters: while mean values represent consistency, the coefficient of variation quantifies the scatter. The predictions were expressed in terms of the normalized mean crack width. The statistical results are presented in Fig. 2 with crack widths taken at the reinforcement stress ${\sigma }_{s}=250\,\text{MPa}$ representing the service load. For some of the members with the maximum reinforcement stress being below 250 MPa or stress at first cracking being above 250 MPa, the values closest to 250 MPa were taken. Two specimens were excluded from the original tests of Farra and Jaccoud [8] as ${\sigma }_{s}$ exceeded 400 MPa at the formation of first crack.

Fig. 2.

Mean crack width (${w}_{m}$) predictions for RC ties from the study of Wu and Gilbert [7] and Farra and Joccoud [8]

The results presented in Fig. 2 indicate that the newly proposed model has demonstrated superior accuracy regarding the design code methods in terms of scatter. For the PSM, the coefficient of variation was 21% compared to 23 and 34% for Model Code 2010 [5] and Eurocode 2 [6], respectively. However, the mean value for the PSM was not safe with the prediction being ≈11% below the test. Model Code 2010 predictions were also unsafe (≈−24%), whereas only Eurocode 2 gave safe predictions (≈+14%). It is worth mentioning that the underestimation of the crack width using PSM could be the fact that the shrinkage of concrete was neglected (assumption 7).

3.2 Analysis of RC Beams

Although the model was originally derived using singly reinforced tensile member, due to practical reasons, it is worth checking its capability to predict mean crack width of bending members.

The analysis considers 4 RC beams from the well-known tests reported by Rüsch and Rehm [9]. Main characteristics of the beams are presented in the Table 2 and Fig. 3. The bending members were reinforced with high–bond steel bars having similar bottom and lateral cover thicknesses. The members were tested under a four–point bending scheme with mean crack width (${w}_{m}$) defined at the reinforcement level within the 2 m pure bending zone. The ${w}_{m}$–${\sigma }_{s}$ graphs for each of the beams are presented in Fig. 4. To quantify the prediction accuracy of different models, the numerical ${w}_{m}$ values at steel stress ${\sigma }_{s}=250\, \text{MPa}$ are given in the Table 3.

In general, the ${w}_{m}$ predictions for three methods were quite accurate and close to each other. However, it should be noted that the Pure Shear Method gives a slightly lower variation compared to the other two theoretical models – Eurocode 2 [5] and Model Code 2010 [6].

Table 2. Bending members from the study of Rüsch and Rehm [9]

Fig. 3.

Main cross section parameters of 4 beams reported by Rüsch and Rehm [9].

Fig. 4.

Mean crack width (${w}_{m}$) versus reinforcement stress (${\sigma }_{s}$) for test beams from the study of Rüsch and Rehm [9]

Table 3. Statistical analysis of the average crack width of the bending members from the study of Rüsch and Rehm [9]

4 Conclusions

• A new simplistic approach for modeling crack width of RC members subjected to short–term loading is proposed. The model assumes sole elastic shear stresses occurring in the cover thickness of concrete and, thus, allows to simply calculate one of the most essential parameters closely related to SLS – mean crack width.

• To check the capability of Pure Shear Method (PSM) to predict mean crack width of RC ties, a comparative analysis employing experimental results of 125 tensile members reported by Wu and Gilbert and Farra and Joccoud as well as theoretical results predicted by the new model, Eurocode 2 and Model Code 2010 was performed. It was indicated that, at the chosen reinforcement stress level of 250 MPa, representing service load, regarding the correspondence to the experimental results, PSM crack width predictions tends to give slightly lower variation ($COV=21\%$) compared to other 2 models – Eurocode 2 ($COV=34\%$) and Model Code 2010 ($COV=23\%$). However, it was observed that the newly proposed model and Model Code 2010 on average tends to give slightly smaller mean crack width values compared to experiment.

• A possibility to predict mean crack width of bending members subjected to short–term loads using Pure Shear Method was also tested. For the mean crack width validation 4 bending members from the experimental program of Rüsch and Rehm were chosen. The predictions by the new model were also compared to the results obtained using Eurocode 2 and Model Code 2010. It was indicated that, at the chosen reinforcement stress level of 250 MPa, regarding the correspondence to the experimental results, the new model tends to give slightly lower variation ($COV=17\%$) compared to other 2 models – EC2 ($COV=24\%$) and MC2010 ($COV=19\%$).