Partial Shape Similarity by Multi-metric Hamiltonian Spectra Matching

Abstract

Estimating the similarity of non-rigid shapes and parts thereof plays an important role in numerous geometry analysis applications. We propose a method for evaluating the similarity and matching of shapes describing articulated objects that gracefully handles partiality. The correspondence between a part and a whole is formulated as the alignment of spectra of operators closely related to the Laplace-Beltrami operator (LBO). The proposed approach considers multiple metrics defined on the same surface, which provide a compact description of the underlying geometric structure from different perspectives. Specifically, we study the scale-invariant metric and the corresponding scale-invariant Laplace-Beltrami operator (SI-LBO) together with the regular metric and the regular LBO. We demonstrate that, unlike the regular LBO, the low pass part of the SI-LBO eigen-structure is sensitive to regions with high Gaussian curvature which are of semantic importance in articulated objects. Thus, the low part of the SI-LBO’s spectrum better captures curved regions and complements the information encapsulated in the lower part of the regular LBO’s spectrum. A two spectra matching loss lends itself to a method that outperforms state of the art axiomatic and learning based techniques when evaluated on the task of partial matching on well established benchmarks (Code and results are available at: https://github.com/davidgip74/DualSpectraAlignmnent).

1 Introduction

Non-rigid shape matching is a fundamental task in many computer vision applications such as augmented reality, medical image analysis, and face recognition. Aligning shapes captured in real-world scenarios, where occlusions and partial views are common, is particularly difficult when considering the missing information. Some recent papers [3, 15, 16, 18, 21, 23] address this challenge by introducing methods for partial shape matching.

In 2019, Rampini et al. [21] addressed the problem by matching a part of a given shape to the whole. The matching region in the full shape is found by aligning the eigenvalues of differential operators closely related to the LBO. Unlike methods that rely on local descriptors that produce dense point-to-point correspondences, the region matching formulation adopts a global perspective that makes it inherently resilient to local discrepancies [14]. Such spectral-based region matching can be adapted to challenging settings such as matching approximately isometric shapes or shapes with missing parts. In this paper we continue the shape-DNA [22] line of thought, and the more recent efforts [8, 17, 20], that argue that the eigenvalues of the Laplace-Beltrami operator (LBO), known as spectrum, could be used as shape descriptors. Exploiting this idea, we adopt and adapt the potential alignment method proposed in [21] and define a combination of two Hamiltonian operators [7] by which the shape matching by spectrum alignment is performed.

Roughly speaking, the LBO spectrum captures the surface structure as a whole. It therefore has a global flavor that limits its ability to describe fine details [19, 21] that are associated with local geometric structures of regions with high Gaussian curvature. We demonstrate that the spectrum of the scale-invariant LBO [2] depends mainly on curved regions which usually contain meaningful details, like joints and fingertips, that are essential when considering articulated objects. The complementary structures captured by each of the two spectra, that share the same support, motivates the proposed multi-metric approach. To demonstrate the advantage of this approach, we first show that comparing the dual spectra of full shapes results in improved separation of closely related classes of shapes, such as dogs and wolves. We then study the problem of matching a part of a shape to its whole. We demonstrate that matching two spectra allows to lock onto fine details that are missed when aligning a single spectrum.

The main contributions of this paper include,

• Matching part of a shape to its whole using more than a single metric defined on the same surface.

• A theoretical interpretation of the scale-invariant LBO spectrum as an indicator of regions with high Gaussian curvature that are semantically important when describing articulated objects.

• Outperforming state of the art learning and axiomatic methods for partial shape matching tested on challenging benchmarks like SHREC’16 CUTS [9] and PFARM [3, 13].

2 Background

Shapes as Riemannian Manifolds. We model a shape as a Riemannian manifold $\mathcal {M} = (S,g)$, where S is a smooth two-dimensional surface embedded in $\mathbb {R}^3$ and g a metric tensor, also referred to as first fundamental form. The metric tensor defines geometric quantities on the surface, such as lengths of curves and angles between vectors. Note, that the same surface S with a different metric $\tilde{g}$ can be used to define a different manifold $\tilde{\mathcal {M}}= (S,\tilde{g})$.

2.1 The Laplace-Beltrami Operator

The Laplace-Beltrami operator (LBO) ${\varDelta _{g}}$ is an ubiquitous operator in shape analysis. It generalizes the Laplacian operator to Riemannian manifolds,

$$\begin{aligned} \varDelta _g f \triangleq \frac{1}{\sqrt{|g|}} \text {div} (\sqrt{|g|} g^{-1} \nabla f) \, , \, \, f \in \mathcal {L}^2(\mathcal {M}) \,, \end{aligned}$$

(1)

where |g| is the determinant of g, and ${\mathcal {L}^2(\mathcal {M})}$ stands for the Hilbert space of square-integrable scalar functions defined on $\mathcal {M}$.

The LBO admits a spectral decomposition under homogeneous Dirichlet boundary conditions,

$$\begin{aligned} -\varDelta _{g} \phi _i(x)&= \lambda _{i} \phi _i(x) \, ,&x&\in \mathcal {M} \setminus \partial \mathcal {M} \nonumber \\ \phi _i(x)&= 0 \, ,&x&\in \partial \mathcal {M} \end{aligned}$$

(2)

where $\partial \mathcal {M}$ stands for the boundary of manifold $\mathcal {M}$. The set ${\{ \phi _i\}_{i\ge 0}}$ constitutes a basis invariant to isometric deformations. It can be regarded as a generalization of the Fourier basis [26].

2.2 The Hamiltonian Operator in Shape Analysis

In 2018, Choukroun et al. [7] adapted the well-known Hamiltonian operator $\text {H}_{g}$ from quantum mechanics to shape analysis,

$$\begin{aligned} \text {H}_{g} \triangleq -\varDelta _{g} + v, \end{aligned}$$

(3)

with $v: S \rightarrow \mathbb {R}^{+}$. $\text {H}_{g}$ is a semi-positive definite operator that admits a spectral decomposition under homogeneous Dirichlet boundary conditions.

Fig. 1.

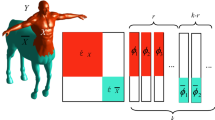
Top: First eigenvectors of the LBO of the partial shape $\mathcal {N}$. Bottom: First eigenvectors of the Hamiltonian of the full shape $\mathcal {M}$. The Hamiltonian is defined with a step potential v (in black) corresponding to the effective support of $\mathcal {N}$. With the potential v, the eigenfunctions of the LBO and the Hamiltonian are similar up to a sign.

The Hamiltonian operator was first introduced to shape analysis in [7] where a comprehensive survey in this context could be found, see also [12]. For our discussion, the most important property of the Hamiltonian is,

Property 1

Let $\mathcal {M} =(S,g)$ be a Riemmanian manifold and ${v: S \rightarrow \mathbb {R}^{+}}$ a potential function. The absolute value of eigenfunctions $\phi _i$ of the Hamiltonian exponentially decay in every ${\hat{s} \in S}$ for which ${v(\hat{s}) > \lambda _i}$.¹

Figure 1 illustrates that the potential can be considered as a mask determining the domain at which the LBO embedded in the Hamiltonian is effective. A second key property of the Hamiltonian is the differentiability of its eigenvalues with respect to its potential function [1].

Property 2

The eigenvalues $\{ \lambda _i \}_{i\ge 0}$ of the discretized Hamiltonian operator $\textbf{H}$ are differentiable with respect to the potential v.

3 A Single Surface Treated as Two Manifolds

Shape properties, including the notion of similarity itself, are affected by the choice of a metric. Two surfaces can be isometric w.r.t. one metric and non-isometric w.r.t. another, see examples in [11]. Considering multiple metrics for the same surface can therefore be viewed as considering alternative perspectives of the same shape, each being sensitive to different types of deformations. Specifically, we use the regular and the scale-invariant metrics. The leading eigenvalues in the spectrum of the SI-LBO are influenced by regions with high Gaussian curvature like joints and fingertips which are essential in representing articulated shapes. The LBO leading eigenvalues, at the other end, treat all surface points alike, and are thus less sensitive to these geometric structures.

3.1 Scale Invariance as a Measure of Choice

Scale Invariant Metric. One version of a scale-invariant metric for surfaces utilizes the Gaussian curvature K [10] as local scaling of the regular metric elements. A scale invariant pseudo-metric $\tilde{g}$ can be defined by its elements as,

$$\begin{aligned} \tilde{g}_{ij} \triangleq |K| \, g_{ij} \,, \end{aligned}$$

(4)

where $g_{ij}$ are the elements of the regular metric tensor. Adding a small positive constant $\epsilon \in \mathbb {R}^+$ to the Gaussian curvature, so that, $\tilde{g}_{ij} = \sqrt{\epsilon +K^2} \, g_{ij}$, defines a metric. The modulation by a Gaussian curvature conformally shrinks intrinsically flat regions into points. The LBO of a Riemmanian manifold $\tilde{\mathcal {M}}$, defined by the surface S equipped with the scale-invariant metric $\tilde{g}$ is called the scale-invariant Laplace-Beltrami Operator (SI-LBO) [2],

$$\begin{aligned} \varDelta _{\tilde{g}} = |K|^{-1}\varDelta _g. \end{aligned}$$

(5)

Scale-Invariant Metric and Articulated Objects. The scale-invariant metric inflates semantically important regions in articulated objects. Figure 2 shows the curvature magnitude for some shapes from SHREC’16 [9]. In the human case, for instance, the scale invariant metric accentuates the head, the hands and the feet, at the expense of flat regions such as the back and the legs. Intuitively, the scale-invariant metric shrinks intrinsically flat regions into points and inflates intrinsically curved regions. We formalize this intuition in the spectral domain with a direct generalization of the Weyl law for the SI-LBO.

Fig. 2.

Absolute value of the Gaussian curvature texture mapped to shapes from TOSCA [6]. Regions with large curvature magnitudes are darker, and have a larger influence on the spectrum of the SI-LBO, according to Theorem 1. These regions contain important details that can be used to classify an object.

Lemma 1

Let $\tilde{\mathcal {M}} = (S: \varOmega \subseteq \mathbb {R}^2 \rightarrow \mathbb {R}^3, \tilde{g})$ be a Riemmanian manifold defined with the scale-invariant metric tensor ${\tilde{g}}$ and $\{\tilde{\lambda }_i \}_{i\ge 1}$ the spectrum of the scale-invariant LBO of $\tilde{\mathcal {M}}$. It holds, $\tilde{\lambda }_i \sim \frac{2\pi i}{\int _{\omega \in \varOmega } |K(\omega )| da(\omega )}$, where $\sim$ stands for asymptotic equality.

Using Lemma 1, a simple perturbation analysis expresses the influence of the curvature on the spectrum of the SI-LBO.

Theorem 1

Consider a perturbation $\epsilon \, \delta _p$ of the curvature at $p \in \tilde{\mathcal {M}}$ where $\epsilon >0$ and $\delta$ is a Dirac delta function on $\tilde{\mathcal {M}}$. Denote by $\delta K \triangleq \frac{\int _{\varOmega }{\epsilon \, \delta _p(\omega )} da(\omega )}{\int _{\varOmega } |K(\omega )| da(\omega )}$ the relative perturbation of the curvature and by $\delta \tilde{\lambda }_{i} \triangleq \frac{\tilde{\lambda }_i - \tilde{\mu }_i}{\tilde{\lambda }_i}$ the relative perturbation of $\tilde{\lambda }_i$, where $\tilde{\mu }_i$ is the $i^{th}$ eigenvalue of the perturbed manifold. $\delta \tilde{\lambda }_i$ respects $\delta \widetilde{\lambda }_i \sim \delta K \,$.

Theorem 1² implies that the SI-LBO spectrum is mostly determined by regions with effective Gaussian curvature. To illustrate the benefits of the proposed multi-metric approach and the scale-invariant metric for matching articulated shapes, we apply the ShapeDNA representation by using the spectra of both the LBO ${\{\lambda _{i}\}^{k}_{i=1}}$ and the SI-LBO ${\{\tilde{\lambda }_i\}^{k}_{i=1}}$, defined for each shape. We normalize each spectrum to balance the two. As shown in Fig. 3, the incorporation of the SI-LBO results in a clear separation of shape classes such as quadrupeds like horses, cats, dogs, wolves, and humans, that can not be separated when only the LBO spectrum is considered.

Fig. 3.

Multidimensional scaling mapping to the plane applied to the distances between truncated spectra of the LBO (left) and that of the LBO together with the SI-LBO (right) for shapes from TOSCA [6]. Points that share the same color represent shapes of the same object in different poses. (Color figure online)

4 Dual Spectra Alignment for Region Localization

Overview. In this section we introduce a framework that finds the effective support of a given part of a shape in a shape given as a whole. Following [21], we use Property 1 to reduce the localization of a partial shape within a full shape to a search for a Hamiltonian’s potential v that represents the effective support of the partial shape. The search for the proper potential function is formulated by an alignment cost of the spectra of Hamiltonian operators defined on the full shape with the spectra of the Laplace-Beltrami operators defined on the partial shape. Finally, Property 2 allows the minimization of the cost function with a first-order optimization algorithm.

Notations. The full shape equipped with the regular metric is denoted by ${\mathcal {M}=(S_f, g)}$ and the spectrum of the Hamiltonian defined over ${\mathcal {M}}$ by ${\{\lambda _i\}^{k}_{i=1}}$ with ${\lambda _1 \le ... \le \lambda _k}$. ${\, \tilde{\mathcal {M}}=(S_f, \tilde{g})}$ stands for the full shape defined with the scale-invariant metric and ${\{\tilde{\lambda }_i\}^{k}_{i=1}}$, with ${\tilde{\lambda }_1 \le ... \le \tilde{\lambda }_k}$, for the spectrum of the scale-invariant Hamiltonian. We denote by ${\varPhi \in \mathbb {R}^{n \times k}}$ and ${\tilde{\varPhi } \in \mathbb {R}^{n \times k}}$ the k first eigenfunctions of the discrete versions of the Hamiltonian and of the scale-invariant Hamiltonian, respectively. In the same way, the partial shape equipped with the regular and the scale-invariant metrics are referred to as ${\mathcal {N}=(S_p, g), \, \tilde{\mathcal {N}}=(S_p, \tilde{g})}$. The spectra of the discrete versions of the LBO and of the SI-LBO are respectively denoted by ${\{\mu _i\}^{k}_{i=1}}$ and by ${\{\tilde{\mu }_i\}^{k}_{i=1}}$, with ${\mu _1 \le ... \le \mu _k}$ and ${\tilde{\mu }_1 \le ... \le \tilde{\mu }_k}$.

Cost Function. We consider a cost function that measures the alignment of the LBO spectrum of $\mathcal {N}$ and the SI-LBO of $\tilde{\mathcal {N}}$ with the spectra of the regular and the scale-invariant Hamiltonians of $\mathcal {M}$ and $\tilde{\mathcal {M}}$. Namely,

$$\begin{aligned} f(v)= & {} \Vert \lambda (v) -\mu \Vert ^{2}_{w} + \Vert \tilde{\lambda }(v) - \tilde{\mu }\Vert ^{2}_{w} \,. \end{aligned}$$

(6)

Following [21], the weighted L2 norm ${\Vert .\Vert _w}$ is defined as,

$$\begin{aligned} \Vert a - b\Vert ^{2}_{w}= & {} \sum ^{k}_{i=1} \frac{1}{b_{i}^{2}} (a_i - b_i)^2 \,, \end{aligned}$$

(7)

to mitigate the weight given to high frequencies.

Optimization. The cost function Eq. (6) induces a constrained optimization problem,

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{\text {v} \ge 0} f(v) \,. \end{aligned}$$

(8)

According to Property 2 and [1], the gradient of the last equation with respect to v is,

$$\begin{aligned} \nabla _{v}f= & {} 2 {\textbf {A}} \, (\varPhi \otimes \varPhi ) ((\lambda - \mu ) \oslash \mu ^2) + \,2 \, {\textbf {A}} {\textbf {|K|}} (\tilde{\varPhi } \otimes \tilde{\varPhi }) ((\tilde{\lambda } - \tilde{\mu }) \oslash \tilde{\mu }^2) \,. \end{aligned}$$

(9)

where $\oslash$ stands for point-wise division, $\otimes$ for the point-wise multiplication and ${\textbf {A}}$ for the mass matrix of the discretization of $\mathcal {M}$. To simplify the optimization process, we minimize an unconstrained relaxation of Eq. (8) instead,

$$\begin{aligned} \mathop {\mathrm {arg\,min}}\limits _{v} f(q(v)) \,, \end{aligned}$$

(10)

with $q: \mathbb {R} \rightarrow \mathbb {R}^{+}$ a smooth function operating element-wisely. We consider the saturation function $q(x) = \text {c} (\text {tanh}(x) + 1)$ with $\text {c} \gg \mu _k$. By promoting high step potentials, q limits the eigenfunctions that can be considered within the region where $v \approx 0$. Equation (10) is finally minimized with a trust-region procedure [28], a first order optimization algorithm.

Initialization Strategy for the Dual Spectra Alignment. We follow the initialization procedure described in [21], where the proposed method is performed over multiple initial potentials. The final solution is selected by comparing the projections of the SHOT descriptors [24] onto the first eigenfunctions of the regular and the scale-invariant Hamiltonian of the full shape, with the projection of SHOT descriptors [24] onto the first eigenfunctions of the LBO and the SI-LBO of the partial shape.

Gaussian Curvature Estimation. The Gaussian curvature K is approximated with the Gauss-Bonnet formula. We smooth the result to overcome discretization artifacts. For each vertex, we take the average of the approximated Gaussian curvatures obtained at the first ring neighbors. Moreover, following [2, 5, 11], we use the metric,

$$\begin{aligned} \tilde{g}_{ij}= & {} (\sqrt{\epsilon + K^2})^{\alpha } g_{ij}, \end{aligned}$$

(11)

with $\alpha \in [0, 1]$, which interpolates between the regular, for $\alpha =0$, and the scale-invariant metric, for $\alpha =1$. Interestingly, the introduction of the parameter $\alpha$ is meaningful in light of the interpretation of the scale-invariant metric proposed in Sect. 3.1. $\alpha$ regulates the influence of the shape prior and quantifies the importance given to features found in curved regions. In all our experiments we used $\alpha = 0.33$ and $\epsilon =10^{-8}$.

Table 1. Quantitative analysis of the proposed method compared to state-of-the-art techniques applied to SHREC’16 CUTS [9] and PFARM [3, 13]. The proposed framework achieved state-of-the-art results compared to both learning and axiomatic competing methods.

Fig. 4.

Region localization. Comparison of the proposed approach for partial shape similarity with competing state of the art methods applied to SHREC’16. Red regions correspond to parts on the full shapes that should match the query parts (left column). IoU is indicated below each mask.

Fig. 5.

Quantitative analysis. Cumulative IoU of each method on SHREC’16 CUTS. Areas under the curves are the mean IoUs reported in Table 1.

5 Experiments

5.1 Datasets

We evaluate the dual spectra alignment method on two databases. The first is SHREC’16 Partial Matching Benchmark (CUTS) [9], the standard benchmark to train and assess partial non-rigid shape matching frameworks. It contains 120 partial shapes from 8 classes: dog, horse, wolf, cat, centaur, and 3 human subjects. The partial shapes are obtained by cutting full shapes that have undergone various non-rigid transformations with random planes. The second is PFARM [3, 13], an extension of the FARM test set [13] proposed in [3]. PFARM contains 27 test pairs of humans with significantly different connectivity and vertex density. Shapes that make up a test pair are taken from different human individuals and are therefore only approximately isometric, see Fig. 6. PFARM allows to evaluate the generalization ability of the models in challenging setups which are closer to real-life applications.

5.2 Competing Methods

The proposed method is compared to state of the art methods for partial shape matching. The axiomatic methods we compare to are the spectrum alignment procedure proposed by Rampini et al. [21], Partial Functional Correspondences (PFC) [23], and a bag-of-words aggregation [27] of SHOT descriptors [24]. We also consider DPFM [3], the state of the art learning based method for partial shape matching. It has been shown to be superior to competing learning approaches such as [25]. Please refer to [3] for further comparisons with learning based methods. We use the original codes published by the authors. For DPFM [3], SHREC’16 [9] was split into three folds. Training was performed on two folds, keeping each time a third fold apart for evaluation.

5.3 Results

Comparison to State of the Art Methods. We compare the performance of the proposed dual spectra alignment procedure to existing methods using intersection over union (IoU) as the standard measure of quality. As shown in Fig. 5, our method achieves better results than competing approaches and improves upon the current state of the art in the SHREC’16 CUTS dataset by 12.4%, as demonstrated in Table 1. Table 1 also shows the precision and recall of the different methods. Notably, DPFM [3] and PFC [23] achieve high precision but low recall, due to many-to-one mappings that occasionally result when deriving a point-to-point map from a predicted functional map and lead to fragmented masks. In contrast, our method, which does not rely on local descriptors, avoids such discrepancies. Qualitative comparisons of the proposed method with alternatives on shapes from the SHREC’16 dataset are shown in Fig. 4. This figure illustrates the benefits of the multi-metric approach in detecting important parts such as the head of the third object or the tail of the centaur, which are missed by the single metric approach [21].

Fig. 6.

The proposed region localization procedure applied to approximately isometric, low resolution shapes from PFARM [3, 13].

Generalization Tested on Challenging Datasets. When comparing to the state of the art learning methods, generalization could become an issue. To that end, we trained DPFM on SHREC’16 and evaluated on PFARM. Table 1 shows that the proposed method significantly outperforms DPFM [3] and has an advantage when processing new databases with unknown shapes and challenging setups such as approximate isometries and inconsistent discretizations.

Fig. 7.

Ablation study. Comparison of the proposed multi-metric approach, which includes the spectra of both the LBO and SI-LBO, with a method based only on the spectrum of the LBO and the SI-LBO spectrum. The plot shows the cumulative score of each setup tested on SHREC’16 [9]. The multi-metric approach reaches a mean IoU of 0.75. The single metric approach, involving only the LBO, mean IoU is 0.71. While using only the SI-LBO the mean IoU is 0.7.

5.4 Ablation Study

Multi-metric vs Single Metric. To demonstrate the benefits of the multi-metric approach for region localization, we compare the alignment of single and multiple spectra considering the same number of eigenvalues. Figure 7 shows the cumulative IoU of the proposed framework applied to SHREC’16 [9] while using 20 eigenvalues of the LBO and 20 eigenvalues of the SI-LBO. It is compared to one setup with 40 eigenvalues of the LBO (without SI-LBO) and to a second setup with 40 eigenvalues of the SI-LBO (without LBO). The region alignment problems are thereby solved with the same number of constraints for each problem. Figure 7 shows that the multi-metric approach clearly outperforms single metric approaches.

6 Future Research Directions

We proposed a novel approach for shape similarity that leverages the complementary perspectives offered by the regular and scale-invariant metrics to achieve performance improvements compared to state of the art methods. In future research, we plan to extend the proposed spectra alignment procedure to more challenging datasets such as SHREC’16 Partial Matching (HOLES) [9]. It could be done by exploring new metric spaces and differentiable shape representations that also adopt a multi-metric perspective, such as self-functional maps [11]. Finally, the proposed method is fully differentiable and can potentially serve as an unsupervised loss to train a learning framework for partial shape matching.