Quantum Circuit Compilation for the Graph Coloring Problem

Abstract

In this work we investigate the performance of greedy randomised search (GRS) techniques to the problem of compiling quantum circuits that solve instances of the Graph Coloring problem. Quantum computing uses quantum gates that manipulate multi-valued bits (qubits). A quantum circuit is composed of a number of qubits and a series of quantum gates that operate on those qubits, and whose execution realises a specific quantum algorithm.

Current quantum computing technologies limit the qubit interaction distance allowing the execution of gates between adjacent qubits only. This has opened the way to the exploration of possible techniques aimed at guaranteeing nearest-neighbor (NN) compliance in any quantum circuit through the addition of a number of so-called swap gates between adjacent qubits. In addition, technological limitations (decoherence effect) impose that the overall duration (i.e., depth) of the quantum circuit realization be minimized.

One core contribution of the paper is the application of an upgraded version of the greedy randomized search (GRS) technique originally introduced in the literature that synthesises NN-compliant quantum circuits realizations, starting from a set of benchmark instances of different size belonging to the Quantum Approximate Optimization Algorithm (QAOA) class tailored for the Graph Coloring problem. We propose a comparison between the presented method and the SABRE compiler, one of the best-performing compilation procedures present in Qiskit, an open-source SDK for quantum development, both from the CPU efficiency and from the solution quality standpoint.

1 Introduction

Quantum algorithms process information represented as qubits, the basic unit of quantum information, and quantum operations (called gates) are the building blocks of quantum algorithms. In order to be run on real quantum computing hardware, quantum algorithms must be compiled into a set of elementary machine instructions (or gates). Since currently available quantum devices suffer a number of technological problems such as noise and decoherence, it is important that the process that carries out the quantum computation be somehow adapted to the physical limitations of the quantum hardware of interest, by means of a proper compilation.

For practical applications, it is essential to make quantum computation able to tackle problem instances of more and more realistic size. To this aim, the ability to produce compiled quantum circuits of good quality is of paramount importance. In this paper, we focus our efforts on the so-called Quantum Alternate Operator Ansatz (QAOA) algorithms [9] applied on the gate-model noisy intermediate-scale quantum (NISQ) processor units [18]. Our approach intends to improve over the compilation algorithms employed in the Qiskit quantum computing software development kit [1], and devise solutions that are easily adaptable to different classes of problems. In the NISQ era, the leading quantum processors are characterized by about 50 to a few hundred qubits but are not advanced enough to reach fault tolerance, nor large or sophisticated enough to continuously implement quantum error correction. The term “noisy” refers to the fact that quantum processors are very sensitive to the environment and may lose their quantum state due to quantum decoherence. The term “intermediate-scale” refers to the relatively small number of qubits and moderate gate fidelity. The term NISQ algorithms refers to algorithms designed for NISQ quantum processors. For example, the Variational Quantum Eigensolver (VQE) or the Quantum Alternate Operator Ansatz (QAOA) (and its sub-class, the Quantum Approximate Optimization Algorithm [6, 8]) are hybrid algorithms that use NISQ devices but reduce the calculation load by implementing some parts of the algorithm in usual classical processors.

Usually, NISQ algorithms require error mitigation techniques to recover useful data, which however make use of precious qubits to be implemented. Thus, the creation of a computer with tens of thousands of qubits and sufficient error correction capabilities would eventually end the NISQ era. These “beyond-NISQ” devices would be able, for example, to implement Shor’s algorithm, for very large numbers, and break RSA encryption. Until that point however, the need to produce circuits runnable in the current (or near-future) quantum architectures in a reasonably reliable manner (i.e., counting on noise minimization techniques rather than on error-correcting techniques) will stand. Hence, the need to provide quantum circuit compilation procedures that minimize the effects of decoherence by minimizing the circuit’s depth.

In this work, we investigate the performance of an upgraded version of the greedy randomized search (GRS) technique [10, 16, 19] originally introduced in [17] applied to the problem of compiling quantum circuits to emerging quantum hardware. In particular, we experiment on a set of benchmark instances belonging to the Quantum Alternate Operator Ansatz (QAOA) class tailored for the Graph Coloring problem, and devised to be executed on top of a hardware architecture inspired by Rigetti Computing Inc. [20]. We compare our algorithm’s performance against the SABRE compiler [13], one of the best compilers present in the Qiskit framework, and demonstrate the superiority of our approach.

The paper is organized as follows. Section 2 provides some background information. Section 3 formally describes the problem, whereas Sect. 4 describes the proposed heuristic solving algorithms and the Greedy Randomised Search approach. Finally, an empirical comparison with the results obtained from the SABRE compiler [1] and some conclusions close the paper.

2 Background

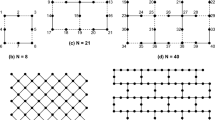
Quantum computing is based on the manipulation of qubits rather than conventional bits; a quantum computation is performed by executing a set of quantum gates on the qubits. A gate whose execution involves k qubits is called k-qubit quantum gate. Current NISQ devices only allow the direct execution of 1-qubit and 2-qubit quantum gates. In order to be executed, a quantum circuit must be mapped on a quantum chip which determines the circuit’s hardware architecture specification [14]. The chip can be seen as an undirected multigraph whose nodes represent the qubits (quantum physical memory locations) and whose edges represent the types of gates that can be physically implemented between adjacent qubits of the physical hardware (see Fig. 1 as an example of three chip topologies of increasing size). Since a 2-qubit gate requiring two specific qstates can only be executed on a pair of adjacent (NN) qubits, the required qstates must be made nearest-neighbors prior to gate execution. NN-compliance can be obtained by adding a number of swap gates so that every pair of qstates involved in the quantum gates can be eventually made adjacent, allowing all gates to be correctly executed.

Fig. 1.

Three quantum chip designs characterized by an increasing number of qubits ($N=8,21,40$) inspired by Rigetti Computing Inc. Every qubit is located at a different location (node), and the integers at each node represent the qubit’s identifier.

Figure 2 shows an example of quantum circuit that only uses the first three qubits of the chip ($N=8$) of Fig. 1, which assumes that qstates $q_1$, $q_2$ and $q_3$ are initially allocated to qubits $n_1$, $n_2$ and $n_3$. The circuit is composed of four generic 2-qubit gates (i.e., CNOT gates) and one generic 1-qubit gate (i.e., the Hadamard gate). Note that the circuit is not NN-compliant as the last gate involves two qstates resting on to two non-adjacent qbits ($n_1$ and $n_3$). The right side of Fig. 2 shows the same circuit made NN-compliant through the insertion of a swap gate.

In this work, we tackle the compilation problem of quantum circuit following a scheduling-oriented formulation, as described in the next sections. In particular, our approach is related to a body of heuristic efforts available in the current literature, see [11, 12] for two relatively recent representative works. Even though these papers pursue the same objective, i.e., optimizing the realization of nearest-neighbor compliant quantum circuits, they focus on quantum circuits characterized by pre-ordered non-commutative gates. On the contrary, our approach leverages the parallel nature of the considered planning/scheduling problem, and proposes a greedy randomized algorithm that exploits gate commutativity through a heuristic ranking function for quantum gate selection.

3 The QCC Problem

The problem tackled in this work consists in compiling a given quantum circuit on a specific quantum hardware architecture. To this aim, we focus on the Quantum Alternating Operator Ansatz (QAOA) framework [9] a generalization of the Quantum Approximate Optimization Algorithm (QAOA) circuits [6, 8], a class of hybrid quantum algorithms used in the literature to solve problems like the Max-Cut, while the Graph Coloring problem has received much less attention. The quantum hardware architecture we consider is inspired by the one proposed by Rigetti Computing Inc. [20]. The quantum circuits that solve the benchmark problems considered in this work are characterized by a high number of commuting quantum gates (i.e., gates among which no particular order is superimposed) that allow for great flexibility and parallelism in the solution, which makes the corresponding optimization problem very interesting and allows for an a significant depth minimization potential to limit circuit’s decoherence [21].

Fig. 2.

Example of quantum circuit: (a) not NN-compliant; (b) NN-compliant through the insertion of a swap gate between qbits $n_1$ and $n_2$ just before the last gate, which exchanges the position of their respective qstates. It is implicitly supposed that at the beginning, the i-th qstate is resting on the i-th qubit.

The rest of this section is devoted to: (i) describing the Graph Coloring problem and (ii) providing a formulation of the Quantum Circuit Compilation Problem (QCCP).

3.1 The Graph Coloring Problem

Given a graph G(V, E) with $n = |V|$ nodes and $m = |E|$ edges, the objective is to maximize the number of edges in E that have end points with different colours, using for each node one among k available colours ($k > 2$), see Fig. 3a. Similarly to the MaxCut problem case, the quantum state preparation circuit within the QAOA solving framework relative to the Graph Coloring problem is divided in the following ordered phases: (i) initial state preparation (INIT block), (ii) phase-shift (P-S block), and (iii) mixing (MIX block) (see Fig. 3b).

Specifically, the initial state preparation phase serves the purpose of initializing the quantum states to represent a feasible initial assignment, and its objective is to create a superposition with equal coefficients of all the $k^n$ possible colorings ($W_N$ state [4]), following the one-hot encoding [7]. According to the one-hot encoding, k qubits are required to represent the color of each vertex, where all but the i-th qubit ($1 \le i \le k$) are assigned the value and the i-th qubit, which is assigned the value, indicates whether that node is coloured with the colour i. As a consequence, in order to solve a Graph Coloring instance characterized by n nodes and k colors following the one-hot encoding, it is necessary to use quantum machines with at least nk qubits. More concretely, the feasible initial state assignment is obtained through the utilization of a series of controlled-G(p) rotations followed by an inverted CNOT ($W_N$ gates, see Fig. 3c). The analysis of the specific circuitry necessary to develop the $W_N$ quantum state is beyond the scope of this paper; the interested reader may refer to [4].

The P-S-phase is composed of a series of phase-shift ($R_{ZZ}$) gates whose task is counting the edges colored with different colors. For this purpose, an $R_{ZZ}$ gate (see Fig. 3c) is applied to all the $(k^2 - k)/2$ combinations of different colors associated to the end-points of any edge of the graph to be colored. All the phase-shift gates are commutative, so the compilation process does not need to worry about their order in the final circuit.

Finally, the MIX phase serves the purpose of implementing the rotation of all the k colors on every node on the graph, thus potentially allowing any possible color assignment. The basic component of the MIX phase is the $R_{XX}R_{YY}$ (or $MIX_{XY}$) gate (see Fig. 3c), applied to each vertex of the graph to be colored, and for each pair of adjacent colors in the graph that represents the color rotation on each vertex. The placement of the $MIX_{XY}$ gates in the compiled circuit requires some attention, as these gates are only partially commutative (see the next section).

Fig. 3.

(a) An example of Graph Coloring instance with $k=3$ colors. (b) Schema of the quantum state preparation circuit within the QAOA framework, composed of the initialization block, P-S- (phase-shift) block and MIX block. (c) Decomposition in terms of unary and binary basic gates of the quantum gates that respectively compose the three previous blocks.

Figure 3a shows an example of the graph G that represents a Graph Coloring problem instance composed of 5 vertices, 8 edges and $k=3$ colors. Figure 3b, presents the quantum state preparation schema of the QAOA framework, typically composed of the initial qubit allocation block (state initialization), the P-S (phase-shift) block and the MIX block. In the Graph Coloring problem case, each of the previous three blocks are composed of particular quantum gate aggregations, the $W_N$, the $R_{ZZ}$ (phase-shift), and the $MIX_{XY}$ gates respectively, shown in Fig. 3c. Generally, the P-S and the MIX blocks within the QAOA framework can be executed along multiple passes (p) in order to obtain more accurate results; in the context of this work, we consider quantum circuits composed of two passes ($p = 2$).

3.2 Quantum Gate Compilation Problem

Formally, the Quantum Circuit Compilation Problem (QCCP) is a tuple $P = \langle C_0, L_0, QM \rangle$, where $C_0$ is the input quantum circuit, representing the execution of the Graph Coloring algorithm, $L_0$ is the initial assignment of the i-th qstate $q_i$ to the i-th qubit $n_i$, and QM is a representation of the quantum hardware as a multigraph.

• The input quantum circuit is a tuple $C_0 = \langle Q, V_{C_0}, TC_0 \rangle$, where: (1) $Q = \{q_1, q_2,\ldots ,q_N\}$ is the set of qstates which, from a planning  & scheduling perspective, represent the resources necessary for each gate’s execution (see for example [15], Chap. 15); (2) $V_{C_0} = W_N \cup \textit{P-S} \cup MIX_{XY} \cup \{g_{\textit{start}}, g_{\textit{end}} \}$ represents the set of state initialization, phase-shift and mix gate operations that have to be scheduled. Note that all the previous gates are binary, in the sense that they require two qstates. Note also that $g_{\textit{start}}$ and $g_{\textit{end}}$ are two fictitious reference gate operations requiring no qstates. The execution of every quantum gate requires the uninterrupted use of the involved qstates during its processing time, and each qstate $q_i$ can process at most one quantum gate at a time. (3) Finally, $TC_0$ is a set of simple precedence constraints imposed on the $W_N$, P-S, $MIX_{XY}$ and $\{g_{\textit{start}}, g_{\textit{end}}\}$ sets, such that: (i) each gate in the three sets $W_N$, P-S, $MIX_{XY}$ occurs after $g_{\textit{start}}$ and before $g_{\textit{end}}$; moreover, within the same pass: (ii) every P-S gate must follow any $W_N$ gate with which it shares a qstate; (iii) any $MIX_{XY}$ gate must follow any P-S gate with which it shares a qstate; (iv) all the P-S are totally commutative; (v) a partial ordering exists in the $MIX_{XY}$ set, as follows: the $MIX_{XY}$ is initially partitioned in two sets called $MIX_{odd}$ and $MIX_{even}$ depending on the numbering of their initial qstate; all the gates $mix \in MIX_{odd}$ can commute as they have no qstate in common, and the same applies to all the gates $mix \in MIX_{even}$, while there exists a precedence imposed between a $mix \in MIX_{odd}$ and a $mix \in MIX_{even}$ if and only if they share at least one qstate. Between two consecutive passes, no P-S gate that belongs to the $i+1$-th pass can be executed before any $MIX_{XY}$ gate that belongs to the i-th pass if they share at least one qstate.

• $L_0$ is the initial assignment at the time origin $t=0$ of qstates $q_i$ to qubits $n_i$.

• QM is a representation of the quantum hardware as an undirected multi-graph $QM = \langle V_N, E_{W_N}, E_{\textit{p-s}},$ $E_{swap} \rangle$, where $V_N = \{n_1, n_2, \ldots , n_N\}$ is the set of qubits (nodes), $E_{\textit{p-s}}$, $E_{\textit{swap}}$ or $E_{W_N}$ is a set of undirected edges $(n_i, n_j)$ representing the set of adjacent locations the qstates $q_i$ and $q_j$ of the gates p-s($q_i,q_j$), swap($q_i,q_j$) or $W_N(q_i, q_j)$ can potentially be allocated to. Figure 1 shows an example of quantum hardware.

A feasible solution is a tuple $S = \langle \textit{SWAP}, TC \rangle$, which extends the initial circuit $C_0$ to a circuit $C_S = \langle Q, V_{C_S}, TC_{S} \rangle$, such that $V_{C_S} = \textit{SWAP} \cup W_N \cup \textit{P-S} \cup \textit{MIX} \cup \{g_{\textit{start}}, g_{\textit{end}} \}$ and $TC_{S} = TC_{0} \cup TC$ where: (i) SWAP is a set of additional swap($q_i,q_j$) gates added to guarantee the adjacency constraints for the set of $W_N$, P-S and $MIX_{XY}$ gates, and (ii) TC is a set of additional simple precedence constraints such that:

• for each qstate $q_i$, a total order $\preceq _i$ is imposed among the set $Q_i$ of operations requiring $q_i$, with $Q_i = \{op \in W_N \cup \textit{P-S} \cup MIX_{XY} \cup \textit{SWAP}: \textit{op requires} \, q_i \}$;

• all the $w_N(q_i, q_j)$, p-s($q_i,q_j$), $mix_{XY}(q_i, q_j)$ and swap($q_i,q_j$) gate operations are allocated on adjacent qubits in QM;

• the graph $\langle V_{C_S}, TC_{S}\rangle$ does not contain cycles.

Given a solution S, a path between the two fictitious gates $g_{start}$ and $g_{end}$ is a sequence of gates $g_{start}$, $op_1$, $op_2$, ..., $op_k$, $g_{end}$, with $op_j \in W_N \cup \textit{P-S} \cup MIX_{XY} \cup SWAP$, such that $g_{start} \preceq op_1$, $op_1 \preceq op_2, \dots , op_k \preceq g_{end} \in TC_0 \cup TC_S$. The length of the path is the number of all the path’s gates and depth(S) is the length of the longest path from $g_{start}$ to $g_{end}$. An optimal solution S is a feasible solution characterized by the minimum depth.

4 A Greedy Randomized Search Algorithm

In this section we provide a detailed description of the Greedy Randomized Search (GRS) procedure used to compile the circuit introduced in previous Sect. 3. GRS has traditionally proved to be a very effective method for the resolution of complex optimization problems (such as the QCCP), as it realizes a simple optimization process that quickly guides the search towards good solutions [10, 16, 19]). The GRS is particularly useful in cases where a high-quality solution is needed in a relatively short time. Among other applications, it is particularly suitable for constraint-based scheduling problems; since the QCCP can be reduced to a Planning and Scheduling (P &S) problem [17, 21].

Algorithm 1 depicts the complete randomized search algorithm for generating a near-optimal solutions, which is designed to invoke the CompileCircuit() procedure until a stop criterion is satisfied. It essentially realizes an optimization cycle in which a new solution S is computed at each iteration through the CompileCircuit() algorithm, and its depth (depth(S)) is compared with the best depth found so far (depth($S_{best}$)) in the iterative process. In case depth(S) is smaller than depth($S_{best}$), then the current solution S becomes the new best solution $S_{best}$. The optimization process continues until a stopping condition (generally a max time limit) is met, where the GRS procedure returns the best solution found. As can be readily observed, the efficacy of the GRS mainly depends on the efficacy of the CompileCircuit() procedure (described in the following section), which has the task of synthesizing increasingly better solutions.

4.1 Compile Circuit Algorithm

Algorithm 2 is a randomized algorithm, it operates on macro-gates containing primitive gates that use two qstates at most. Indeed, Algorithm 2 is in itself a heuristically-based iterative algorithm that implements a constructive methodology where a solution is built from scratch using a randomized ranking heuristic. This heuristic returns a ranking among the gates that takes into account the “neighbouring cost" of all the gates that have yet to be inserted in the solution. At each iteration, a subset of gates that guarantee the fastest realization of the neighbouring conditions of all the remaining gates is generated and one gate is selected at random from this subset, for insertion in the current partial solution.

Algorithm 2 takes as input a QCCP problem $P = \langle C_0, L_0, QM \rangle$, and proceeds by chronologically inserting in the partial solution S one gate operation at a time until all the gates in the set $W_N \cup \textit{P-S} \cup MIX_{XY}$ are in S. Let $op \in Q_i$ be a general gate operation that involves qstate $q_i$, we define a chain $ch_i = \{op \in Q_i: op \in S\}$ as the set of gates involving $q_i$ and currently present in the partial solution S, among which a total order is imposed. Let us also define $last(ch_i)$ as the last gate in the chain $ch_i$ according to the imposed total order and $nlast(ch_i)$ as the QM node at which the last operation in the chain $ch_i$ terminates its execution. Finally, we define the state of a partial solution as follows. Given a partial solution S, the state $L_S$ is the tuple $L_S = \langle nlast(ch_1), nlast(ch_2),$ $\ldots , nlast(ch_N) \rangle$ of QM locations (nodes) where each last chain operation $last(ch_i)$ terminates its execution. The first step of Algorithm 2 is the initialisation of the partial solution S; in particular, it sets the current state $L_S$ to the init value $L_0$ by initialising the locations of every qstate $q_i$ (i.e., for every chain $ch_i$) at the time origin¹ $t = 0$.

The core of the algorithm is the function SelectExecutableGate(), which returns at each iteration either one of the gates in the set $W_N \cup \textit{P-S} \cup MIX_{XY}$ or a swap($q_i,q_j$) gate in the $\textit{SWAP}$ set necessary to guarantee NN-compliance as described in the previous Sect. 3.

Indeed, it is a random algorithm targeted to minimize the solution depth, in particular its implementation is inspired to [3], such that the selection of a gate is based on two criteria: (i) the earliest start time gate selection (a value correlated to depth minimization); (ii) a metric to minimize the number of swaps. At each iteration, SelectExecutableGate(P , S , t) selects the next gate to be inserted in the solution by means of the InsertGate(op , S , t) method. In all time instants t where no quantum gate can be selected for insertion, the current time t is increased ($t = t + 1$). In particular, SelectExecutableGate() resembles Algorithm 3 (see [2], page 8) with the following important difference: while the cited Algorithm 3 generates a set of eligible gates $\varOmega$ and then selects a gate at random on the basis the proposed pheromone model (see [2]), the SelectExecutableGate() procedure chooses one gate at random following the same strategy proposed in [17], so that a set of equivalent gates $\varOmega ^*$ is extracted from $\varOmega$ by identifying one gate $op^*$ associated with the minimal lexicographic heuristic value $\varDelta _{sum}(op^*)$ (see [17] for further details on its definition) and by considering equivalent to $op^*$ all the gates op such that $\varDelta _{sum}(op) = \varDelta _{sum}(op^*)$, $\varOmega ^* = \{op: op \in \varOmega , \varDelta _{sum}(op) = \varDelta _{sum}(op^*)\}$. A full description of the procedure SelectExecutableGate() is given in [2]. The randomly selected gate $op \in \varOmega ^*$ is inserted in the partial solution S at the earliest feasible time as the last operation of the chains relative to the qstates involved in op: $last(ch_i) \leftarrow op$; subsequently, the state $L_S$ of the partial solution is updated accordingly. Algorithm 2 proceeds until a complete solution is built.

5 Experimental Evaluation

We have implemented and tested the proposed ideas leveraging the Qiskit open-source quantum-related framework [1]. Qiskit is a known open-source Software Development Kit for working with quantum computers at the level of pulses, circuits and application modules. It allows for the creation, modification, simulation, and optimization of quantum circuits on a set of both simulated and real quantum architectures, as well as allowing the possibility to test mapping algorithms on arbitrary quantum hardware topologies.

Our contribution for this study focuses on the process of quantum circuit compilation with reference to a given hardware topology with the aim of minimizing the circuit’s depth. The proposed procedure was implemented in Python in order to allow its integration within Qiskit. The performance of the algorithm was tested on a benchmark set specifically created to represent the application of quantum computing to the Graph Coloring problem.

5.1 Setup

The benchmark set for the graph colouring circuits is obtained as an extension of part of the N8 benchmark set for the Max-Cut problem [21]. Following the approach in [21], the graph G for which the optimal coloring assignment needs to be found are randomly generated as Erdös-Rényi graphs [5]. In particular, 100 graphs are generated for the $N=8$ qubit case. Half (50 problems) are generated by choosing N of $N(N-1)/2$ edges over 7 qstates randomly located on the circuit of size 8 qubits (referred as ‘Utilization’ $u=90\%$). The other 50 problems are generated by choosing N edges over 8 qstates - referred as utilization $u=100\%$). For the graph colouring benchmark, we only consider the N8 problems with utilization $u=100\%$, and such that the connected graph contains exactly 7 nodes, assigning three colours ($k = 3$) to each node of the graph, for a total of 22 graph instance problems. Hence, quantum processors with at least 21 qubits (7 nodes times 3 colours) are necessary for the execution of such instances (see Sect. 3.1). More specifically, we consider a Rigetti-inspired 21 qubit processor and set $p = 2$ (two PS-mixing passes).

5.2 Results

The Python version of the proposed greedy randomized search (GRS) algorithm compiles a QAOA circuit with the following choices: (i) a one-hot encoding to represent the graph-coloring problems [7], and (ii) a decomposition procedure for the QAOA blocks based on the identification of odd and even $MIX_{XY}$ gates [9, 22], as explained in Sect. 3.2.

Fig. 4.

Comparison between GRS and SABRE

Figure 4 compares the proposed GRS algorithm with the SABRE compiler available in Qiskit (SabreSwap), launched according to its three different heuristics (basic, lookahead, and decay). The algorithms are compared with respect to the depth of the compiled circuits (the circuit’s depth represents the longest path in the compiled circuit graph). For each algorithm, a CPU time limit of 10 seconds is imposed on each run.

From the results in Fig. 4 it is clear that GRS outperforms SABRE in all the latter’s execution modes. One possible explanation for the superiority of GRS is its capability to better exploit the commutativity rules of the gates in the QAOA-based Graph Coloring quantum circuit instances. Indeed, our algorithm imposes no particular order in the selection of the $W_N$, P-S, and $MIX_{XY}$ macro-gates as the solution is built, beyond the precedence constraints originally present in the input quantum circuit, contained in the $TC_0$ set described in Sect. 3.2. As opposed to GRS, SABRE performs the SWAP addition process reasoning directly on the circuit expressed in terms of basic gates, and it is not capable of changing the order of such gates after the circuit is loaded.

6 Conclusions

This study focused on quantum computing as an accelerator for optimization problem resolution. We have considered the compilation techniques for Noisy Intermediate-Scale Quantum (NISQ) devices [18]. In particular, we have explored the Quantum Alternating Operator Ansatz (QAOA) framework [9] for solving optimization problems and studied the quantum circuits for the Graph Coloring reference problem. We have proposed a greedy randomized search (GRS) algorithm targeted at optimizing the compilation of quantum circuits and defined an original benchmark set for testing compilation algorithms. On the basis of our empirical validation the proposed GRS algorithm outperforms other compilation algorithms available in the Qiskit framework.