Keywords

1 Introduction

Monitoring of atmospheric characteristics is an important task in remote sensing of the environment. In this paper, the question is raised about taking into account the influence of clouds on the characteristics of thermal radiation. Atmospheric sounding by the method of receiving atmospheric thermal radiation is the development of ground-based studies of atmospheric thermal radiation. One of the methods of such research is microwave radiometric sounding from artificial Earth satellites. Passive microwave radiometry [1,2,3,4,5] has long been used as a remote sensing approach in geophysics [7, 8], meteorology [9] and astronomy [6, 10, 11]. Observations of the thermal radiation of the atmosphere-ocean surface system [13,14,15] allow us to obtain information about the state of cloud fields in the atmosphere and quantify many meteorological parameters, for example, the mass of water vapor [18], water reserve [17] and the effective temperature of clouds [16]. The disadvantage of a significant part of most previous studies is the use of a homogeneous plane-layered model of the cloud layer, ignoring its heterogeneous structure [20].

Fig. 1.
figure 1

General sketch of the experimental radiometry of cloud fields.

Full size image

Clouds in the troposphere are involved in the scattering and reflection of sunlight and thermal radiation of the atmosphere. For this reason, cloud cover makes a significant contribution to the radiation and energy balance of the atmosphere, which plays a key role in climatic processes on the planet. To understand this role, it is necessary to study the radiation properties of cloud cover. Cloud fields are characterized by a random structure, so their properties are random and can be studied by statistical methods. One of the possible approaches is a direct numerical evaluation of the properties of the cloud fields of interest based on their specific implementations, followed by averaging. This approach is also used in this study.

The aim of this work is to numerically simulate the statistical properties of the thermal radio emission of Plank fields of broken clouds in the microwave range and to study systematic errors of meteorological parameters of the atmosphere associated with the random nature of real broken cloud fields. For this purpose, direct numerical modeling of cloud fields is carried out in the work and the characteristics determining the radio brightness temperatures of broken clouds at various frequencies of the microwave wavelength range are calculated. The calculated characteristics are directly compared with the results obtained in the works of other authors in the study of real fields of broken clouds.

2 Size Distributions and Geometry of Broken Cloud Fields

In the article [12] it is shown that when calculating the characteristics of radiation fields in the microwave range, the assumption of the cylindrical shape of clouds is acceptable.

2.1 The Plank Model

Plank [22] proposed the following distribution:

$$\begin{aligned} n\left( D\right) =Ke^{-\alpha D}, \quad 0\le D\le D_m \end{aligned}$$
(1)

where D is the diameter of the cloud, \(D_m\) is the maximum possible diameter of the cloud in the field, K is a normalization constant, \(\alpha \) is a constant parameter depending on local conditions [22].

The cumulative distribution of the number of clouds by size is, respectively, equal to:

$$\begin{aligned} N\left( D\right) =\frac{1-e^{-\alpha D}}{1-e^{-\alpha D_m}} \end{aligned}$$
(2)

Average diameter of clouds:

$$\begin{aligned} \left\langle D\right\rangle =D_m\left( \frac{1}{\alpha D_m}-\frac{1}{e^{\alpha D_m}-1}\right) \end{aligned}$$
(3)

2.2 Alternative Model

Distribution proposed in [19] based on aircraft measurements over Ukraine:

$$\begin{aligned} n\left( D\right) = KD\cdot \left( 1-\frac{D}{D_m}\right) ^{p_0},\quad 0\le D\le D_m \end{aligned}$$
(4)

where D is the diameter of the cloud, \(D_m\) is the maximum possible diameter of the cloud in the field, K is a normalization constant, \(p_0\) is a constant parameter depending on local conditions [19].

The cumulative distribution of the number of clouds by size is, respectively, writes as follows:

$$\begin{aligned} N\left( D\right) =1-\left( \left( 1+p_0\right) \frac{D}{D_m}+1\right) \left( 1-\frac{D}{D_m}\right) ^{p_0+1} \end{aligned}$$
(5)

Average diameter of clouds, respectively, is

$$\begin{aligned} \left\langle D\right\rangle =\frac{2D_m}{3+p_0} \end{aligned}$$
(6)

2.3 The Cloud Height Distribution

Following the work of [22], the power of the cloud and its diameter can be linked unambiguously by the ratio:

$$\begin{aligned} H=\eta D\left( \frac{D}{D_m}\right) ^\beta \end{aligned}$$
(7)

where \(\eta \) and \(\beta \) are the adjustable model parameters.

Since the height of the cloud is unambiguously related to its diameter by the formula (7), the cloud height in the cloud field is also a random variable with the corresponding statistical distribution. Since in a given model the height of a cloud is uniquely related to its diameter, the probability density of the height distribution is

$$\begin{aligned} p\left( H\right) =\frac{1}{N\left( D_m\right) }n\left( D\right) \frac{dD\left( H\right) }{dH} \end{aligned}$$
(8)

where \(N\left( D_m\right) \) is the total number of clouds in the field. So a certain density of the distribution of random heights of clouds (8) obviously satisfies the condition of normalization by one

$$\begin{aligned} \int _{0}^{D_m}p\left( H\right) dH=1 \end{aligned}$$
(9)

In frequency, for the Plank model of broken clouds (1) probability density of the cloud height distribution \(p\left( H\right) \) is equal to

$$\begin{aligned} P\left( H\right) =\frac{ { (D_m /(\alpha \eta H)) } ^{{\beta }/({\beta +1})} }{\left( 1-e^{-\alpha D_m}\right) \left( \beta +1\right) } \exp \left( {{-{(D_m/\alpha \eta )}^{{\beta }/({\beta +1})}H^{1/{(\beta +1)}} }}\right) \end{aligned}$$
(10)

For the non-Plank model (4) the density function of the height probability distribution is

$$\begin{aligned} P\left( H\right) = \frac{\left( p_0+1\right) \left( p_0+2\right) {\eta ^{{2\beta }/({\beta +1})} }}{H^{(1-\beta )/(\beta +1)} {D_m}^{2/(1+\beta )} (\beta +1)} \left( 1-\left( \frac{H}{\eta ^{\beta } D_m }\right) ^{1/(\beta +1)} \right) ^{p_0} \end{aligned}$$
(11)

It is obvious that the essential parameters of both cloud abundance distributions by diameter (1) and (4) and the corresponding cloud height distributions (10) and (11), the dependence on which is not reduced to a simple linear scaling of the values and arguments of the distribution functions, are in and, respectively, \(\alpha \) and \(p_0\). Otherwise, these distributions can be reduced to dimensionless normalized parameters \(D/D_m\) and \(H/\eta D_m\). In practice, this means that in further research, the values of the parameters \(\eta \) and \(D_m\) can be assumed to be equal to one without limitation of generality. Then, in particular, for \(\beta =0,\eta =1,D_m=1\) for the non-Plank cloud model (11) we get

$$\begin{aligned} p\left( H\right) =\left( 1-H\right) ^{p_0}H\left( p_0+1\right) \left( p_0+2\right) \end{aligned}$$
(12)

This height distribution has a well-defined maximum at \(H=\left( 1+p_0\right) ^{-1}\). For \(\beta =1/2,\eta =1,D_m=1\), respectively, the distribution (11) takes the form

$$\begin{aligned} p\left( H\right) =\frac{2}{3}\left( 1-H^{2/3}\right) ^{p_0}\cdot \root 3 \of {H}\left( p_0+1\right) \left( p_0+2\right) \end{aligned}$$
(13)

with a maximum at

$$\begin{aligned} H=\frac{1}{\sqrt{8p_0^3+12p_0^2+6p_0+1}} \end{aligned}$$
(14)

For \(\beta =-1/2, \eta =1,D_m=1\), respectively, the distribution (11) takes the form

$$\begin{aligned} p\left( H\right) =2H^3\left( 1-H^2\right) ^{p_0}\left( p_0+1\right) \left( p_0+2\right) \end{aligned}$$
(15)

with a maximum at

$$\begin{aligned} H=\frac{\sqrt{3}}{\sqrt{2p_0+3}} \end{aligned}$$
(16)

Probability density distributions (12), (13) and (15) for different values of the parameter \(p_0\) are shown in Figs. 2, 3 and 4, respectively. Thus, these random models of broken clouds can be identified with one of the types of cumulus clouds Cumulus [30] by matching the height of the clouds (according to the maximum probability of distribution or average values) by selecting appropriate combinations of model parameters.

Fig. 2.
figure 2

Probability density functions of the cloud heights distribution (12) for different values of the distribution parameter \(p_0\) (indicated by numbers with corresponding curves).

Full size image

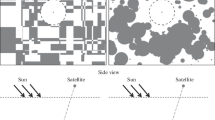
We developed a simple numerical procedure which generates the set of randomly distributed diameters of clouds and then places it randomly over the given rectangular area. The calculation was carried out in the C++ programming language using Intel C++ compiler. The distribution of clouds by size was controlled by the Kolmogorov statistical agreement criterion. The sample random cloud field generated with that procedure is shown in the Fig. 5. Cloud sizes are distributed according the Plank distribution (1) with \(D_m=4\) km and \(\alpha =1.\), \(\beta =0.5\), \(\eta =1.0\). Size of the whole cloud field area is \(100\times 100\) km, relative sky coverage parameter \(S=0.5\).

3 Radiative Properties of the Clouds and the Atmosphere

The total absorption coefficient \(\gamma _\lambda \left( h\right) \) in a cloudy atmosphere consists of molecular absorption in oxygen and water vapor, as well as absorption in small cloud droplets. Absorption in molecular oxygen depends on temperature and pressure, information about it can be found, for example, in [7, 7, 23]. The absorption coefficient in water vapor, in addition, has a close to linear dependence on absolute humidity [21, 23, 24].

The size distribution of droplets of layered clouds and cumulus clouds of good weather is given in [25]. The average droplet sizes of these clouds are 3.9–7.5 microns, and the maximum contribution to the water content is made by droplets with a radius of 10–20 microns [19]. Radar studies by E. Gossard [26] show the presence of droplets with a radius of 70 microns or more in powerful cumulus clouds, and the largest contribution to water content is made by droplets with a size of about 50 microns.

Fig. 3.
figure 3

Probability density functions of the cloud heights distribution (13) for different values of the distribution parameter \(p_0\) (indicated by numbers with corresponding curves).

Full size image

Taking the scattering of microwave radiation on spherical water particles in a cloud by Rayleigh, it is not difficult to obtain the formula [2] for the volume absorption coefficient of the liquid droplet phase in the cloud [20]

$$\begin{aligned} k=\frac{3w}{\rho }k Im{\left( \frac{m^2-1}{m^2+2}\right) } \end{aligned}$$
(17)

where w is the water content of the cloud, \(kg/m^3\), \(\rho \) is the density of water, \(kg/m^3\), \(k=\omega /c\) is the wave number of radiation, m is the refractive index of water.

The coefficients of absorption of radiation by water vapor and the values of total integral oxygen absorption in a vertical column of atmospheric air for different wavelengths can be calculated using the well-known formulas [23]. The complex permittivity of liquid water is determined by the Debye formula (see, for example, [2])

$$\begin{aligned} \varepsilon =\varepsilon _0+\frac{\varepsilon _s-\varepsilon _0}{1+i\frac{\mathrm {\Delta \lambda }}{\lambda }} \end{aligned}$$
(18)

where

$$\begin{aligned} \mathrm {\Delta \lambda }=2\pi \tau _p\frac{\varepsilon _s+2}{\varepsilon _0+2} \end{aligned}$$
(19)

\(\varepsilon _s\) - static permittivity of water (at frequencies \(\nu<<1/\tau _p\)), \(\varepsilon _0=4,9\) - optical permittivity of water (at frequencies \(\nu>>1/\tau _p\)), relaxation time [3]

$$\begin{aligned} \tau _p=exp{\left[ 9,8\left( \frac{273}{T+273}-0,955\right) \right] }\cdot {10}^{-12} s \end{aligned}$$
(20)
Fig. 4.
figure 4

Probability density functions of the cloud heights distribution (15) for different values of the distribution parameter \(p_0\) (indicated by numbers with corresponding curves).

Full size image

The static permittivity of water is described by the approximate formula [3]

$$\begin{aligned} \varepsilon _s\left( T\right) =88,045-0,4147\cdot T+6,295\cdot {10}^{-4}\cdot T^2+1,075\cdot {10}^{-5}\cdot T^3 \end{aligned}$$
(21)

Values of temperature, water reserve and cloud power for Cu cong and Cu med are given in [2, 30]. The altitude profile of the water content of each cloud was calculated using the formula [27, 30]

$$\begin{aligned} w\left( \xi \right) =w\left( \xi _0\right) \frac{\xi ^{\mu _0}\left( 1-\xi \right) ^{\psi _0}}{\xi _0^{\mu _0}\left( 1-\xi _0\right) ^{\psi _0}}=\frac{W}{H}\frac{\mathrm {\Gamma }\left( 2+\mu _0+\psi _0\right) }{\mathrm {\Gamma }\left( 1+\mu _0\right) \mathrm {\Gamma }\left( 1+\psi _0\right) }\xi ^{\mu _0}\left( 1-\xi \right) ^{\psi _0} \end{aligned}$$
(22)

where \(\xi =h/H\) is the reduced height inside the cloud, H is the power of the cloud, km, W is the water reserve of the cloud, \(kg/m^2\), \(w\left( \xi _0\right) \) is the water content of the cloud, \(kg/m^3\), w is the maximum water content clouds, \(\xi _0\) – the reduced height of the maximum water content of the cloud, \(\mu _0,\psi _0\) - dimensionless parameters of the model. According to [30], the parameter values are \(\mu _0=3.27,\psi _0=0.67,\xi _0=0.83\). The dependence of the water reserve of Cumulus-type clouds \((kg/m^2)\) on the cloud power (km) according to the tabular data given in [30] was approximated by the formula

$$\begin{aligned} W=0,132574\cdot H^{2,30215} \end{aligned}$$
(23)
Fig. 5.
figure 5

Sample of the random cloud field model generated with the algorithm developed here. Cloud sizes are distributed according the Plank distribution (1) with \(D_m=4\) km and \(\alpha =1.\), \(\beta =0.5\), \(\eta =1.0\). Size of the whole cloud field area is \(100\times 100\) km, relative sky coverage parameter \(S=0.5\).

Full size image

4 Microwave Thermal Radiation Simulation

In the microwave range, the influence of scattering processes in a cloudy atmosphere can be neglected. If the quantum energy at the radiation frequency is small compared to the temperature \(\hbar \omega \ll kT\), the Planck function is almost proportional to the temperature, which is known as the so-called Rayleigh-Jeans approximation [4, 5]. Thus the observed intensity can be expressed directly in the radio brightness temperature \(T_b\) units (degrees). Under these conditions, and also under the assumption of local thermodynamic equilibrium, the radio brightness temperature of a plane-layered atmosphere when observed from the Earth’s surface can be represented as [28, 29]

Fig. 6.
figure 6

Sounding ray direction.

Full size image
$$\begin{aligned} T_b\left( \lambda ,\theta \right) = \int _{0}^{\infty }{T\left( z\right) \gamma _\lambda \left( z\right) exp{\left( -\int _{0}^{z}{\gamma _\lambda \left( z^\prime \right) sec{\theta }dz^\prime }\right) sec{\theta }}dz} \end{aligned}$$
(24)

where T(z) is the temperature of the atmosphere at an altitude of z, \(\gamma _\lambda \left( z\right) \) is the total absorption coefficient, \(\theta \) is the zenith angle of the viewing direction (see the Fig. 6), \(\lambda \) is the wavelength. Similar integral equation can be written down also for the case of the space-borne observations

$$\begin{aligned} T_b\left( \lambda ,\theta \right) = T_{b0}\,exp{\left( -\int _{0}^{z_0}{\gamma _\lambda \left( z^\prime \right) sec{\theta }dz^\prime }\right) } + \end{aligned}$$
(25)
$$ \int _{0}^{z_0}{T\left( z\right) \gamma _\lambda \left( z\right) exp{\left( -\int _{z}^{z_0}{\gamma _\lambda \left( z^\prime \right) sec{\theta }dz^\prime }\right) sec{\theta }}dz} \,, $$

where \(T_{b0}\) is the radio brightness temperature of the underlying surface.

Fig. 7.
figure 7

2D view of the cloud field portion used for the sample \(T_b\) simulation. Cloud sizes are distributed according the Plank distribution (1) with \(D_m=4\) km and \(\alpha =1.\), \(\beta =0.5\), \(\eta =1.0\). Size of the whole cloud field area is \(50\times 50\) km.

Full size image
Fig. 8.
figure 8

3D view of the cloud field portion used for the sample \(T_b\) simulation. Cloud sizes are distributed according the Plank distribution (1) with \(D_m=4\) km and \(\alpha =1.\), \(\beta =0.5\), \(\eta =1.0\). Size of the whole cloud field area is \(50\times 50\) km.

Full size image
Fig. 9.
figure 9

Sample 2D mapping of the simulated distribution of the radio brightness temperature \(T_b\) (25) observed from space. Random cloud field is shown in the Figs. 7 and 8 over the sea surface (\(T_{b0}=100\, K \)). Viewing zenith angle \(\theta =70^\circ \), radiometer frequency 70 GHz.

Full size image

The expressions (24) and (25) can be immediately integrated numerically, which readily yields the radio brightness temperature \(T_b\). Repeating these calculations for a set of observation points and directions, one gets map of the radio brightness temperatures over the desired sea or land area.

5 Parallelization Efficiency Analysis

Since the integrand does not exhibit any singularities or irregularities, an integration procedure is rather simple. It can be easily parallelized dividing the integration domain or parametrically, using different threads for different sounding ray trajectories. However, for realistic practical purposes these routine calculations should be performed for rather large areas covered by the clouds. In addition, to investigate statistical characteristics of the radio brightness distributions they should be repeated many times. This implies the ultimate need in using high-performance parallel computer systems. The algorithm itself can be implemented using only the basic parallel programming techniques, e.g. the OpenMP or MPI standards.

Since all the integrals (24) and (25) can be evaluated independently from each other, parallelization of these calculations is rather effective both on MPP and SMP architectures. Namely, the computing work can be distributed among any reasonable number of processing cores. Because the threads do not interact with each other, the acceleration is roughly proportional to the number of the cores used. For relatively small cloud fields, SMP architectures are rather effective in practice.

For example, we performed these calculations for the sample portion of the broken cloud field shown in the Figs. 7 and 8 over the sea surface (\(T_{b0}=100\, K \)). The node with 8 computing cores (two 4-core CPUs) was used with the code using OpenMP standard. The result is shown in the Fig. 9. For simpler identification of characteristic features of the cloud field and corresponding features of the radio brightness map, we labeled some of them with the capital letters (A–F). Warm clouds can be clearly seen over the relatively cold sea surface. To account for the instrumental distortions, the calculated \(T_b\) map was convolved with the simple model Point Spreading Function (PSF). The PSF was chosen Gaussian with 2 km half width. This PSF is rather idealistic, however it is used here to show the distortion visually just for the illustrative purposes.

6 Conclusions and Remarks

In the course of the study, algorithms for generating cloud fields were developed based on well-known stochastic models of broken cumulus clouds proposed for real cloud distributions obtained empirically. For the obtained implementations of random cloud fields, numerical estimates of shading curves are made, i.e., the probability of sky overlap in a given direction, depending on the total cloud cover score. The estimates obtained are compared with published observational data on the probabilities of sky overlap.

As a result of the study, the compliance of the models of the broken cloud cover with the known observational data was verified. In addition, the developed algorithms and computer models of cloud fields form a significant practical basis for further studies of radiation processes in the cloud atmosphere.

The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University [31]. The authors thank both reviewers for valuable comments.