Abstract
Jones-optimality determines whether a specializer improves program performances. Reinterpreting this concept in terms of the precision of an abstract interpreter means to determine whether specializing a source program is able to improve the precision of a given static analysis. In the opposite direction, a specializer failing optimality (disoptimal) would decrease the precision of the analysis when applied to the specialized code. In this paper, we exploit this reinterpretation of Jones-optimality relatively to the precision of an abstract interpreter with the aim of systematically deriving obfuscated code. In line with the idea behind Futamura’s projections, we factorize the construction of the obfuscated code by separating specialization and interpretation. An interpreter specializer is then systematically made disoptimal by means of language transduction. The result is a language agnostic code obfuscator which is able to foil any given static analyzer.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Code obfuscation relies upon the idea of making security inseparable from code: a program, or parts of it, are transformed in order to make them hard to understand or analyze [10]. This technology is increasingly relevant in software security, providing an effective way for facing the problem of code protection against reverse engineering. This contributes to comprehensive digital asset protection, with applications in DRM systems, IPP systems, tamper resistant applications, watermarking and fingerprinting, and white-box cryptography [8, 9].
Obfuscation [2] exploits, by a suitably designed program transformation, the intensional nature of program analysis [4, 24], namely the fact that the precision of a program analysis algorithm depends upon the way the program is written and on how data structures are used. The attack scenario here considers the protection of a program—the asset, from an attacker which is implemented by a program analysis algorithm—the so called hostile observer.
In this paper, we consider program analysis as implemented by an abstract interpreter [13]. This is general enough to include most effective sound program analysis algorithms. The abstraction here plays the role of constraining the interpreter (i.e., a Universal Turing Machine) within the boundaries of expressivity as given by the chosen abstract domain. On the one hand, this realizes a case principle in computer security, where the security of a system (e.g., an encryption protocol) is always proved relatively to a constrained attacker, (e.g., by computational complexity). On the other, because any effective attack on code cannot avoid some form of automation of program analysis, this model can fruitfully represent a relevant part of the action of code attack by reverse engineering.
It is known that, by transforming a code we can improve or reduce the precision of any analyzer. It is in general impossible to design a compiler that automatically removes from any program all the false alarms produced by a non straightforward abstract interpreter [4]. However it is instead always possible to inject arbitrary many false alarms by compilation. One of such obfuscating compilers can be simply designed by specializing a suitably designed (called distorted) interpreter [20]. The key observation relies upon the semantic equivalence between the source code and an interpreter specialized on this code. In this case, [26]: (1) The transformed program (resulting from the specialization process) inherits the programming style of the interpreter; (2) The transformed program inherits the semantics of the original program. The reason for (1) is that the transformed program is the result of the specialization of the code of the interpreter. The reason for (2) is that even though the transformed program may be a disguised form of the source code
 , a correct interpreter must faithfully execute the operations that
, a correct interpreter must faithfully execute the operations that
 specifies. It is therefore always possible to act on the intensional properties of programs, and hence on the precision of program analysis, by specializing a suitably designed interpreter [20].
specifies. It is therefore always possible to act on the intensional properties of programs, and hence on the precision of program analysis, by specializing a suitably designed interpreter [20].
Paper Contribution. In this paper we go deeper into building obfuscating compilers by considering the role of the specializer and its interplay with the given interpreter in the action of producing obfuscated code. The notion of Jones optimality [25, 27] helps to give us the compass for understanding the role of program specialization in code obfuscation. Jones optimality was originally introduced to prove whether by compilation it is possible to improve program performance by removing the so called interpretational overhead [27]. We reinterpret Jones optimality in the light of the accuracy of an abstract interpreter. In particular, we show that obfuscating programs by specializing interpreters can be seen as a peculiar, and non-standard, case of Jones-(dis)optimality [25, 27], where, instead of considering performances, we consider precision. We introduce a new notion of optimality (Sect. 5) stating that a specializer is optimal w.r.t. an abstract interpreter if the abstract interpreter is complete (viz. precise [22]) for the resulting program obtained by specializing the concrete interpreter with the source code. Of course, optimal specializers removing all false alarms cannot exist for all programs and non straightforward abstract interpreters, otherwise by the second Futamura projection such compiler would exist [4]. However the degree of optimality of the specializer shows how the specializer is able to remove the imprecision injected by a distorted interpreter. In the case of code flattening, the code obtained by specializing a vanilla interpreter with the source code produces a truly flattened code whenever the program counter is forced to be a dynamic structure [20]. This inhibits a simple specializer to reconstruct the source structure, hence forcing its disoptimal behavior.
On this basis, we derive a constructive technique for building obfuscating compilers which are driven by the property to hide. The distortion phase is built by means of suitable transducers (Sect. 3) that syntactically act on code in order to make a fixed abstract interpreter incomplete for the property to hide. The core structure of our property-driven obfuscating compilers (Sect. 6) is language and property independent. The main conceptual innovation is in the correspondence between a modified version of Jones optimality, where concrete execution time is replaced by the precision of the abstract interpreter, and the process of protecting a program from the analysis obtained by that abstract interpreter. In order to formally characterize this correspondence we need to rethink program interpretation by separating the syntactic parsing from the semantic interpretation ( Sect. 4). This allows us to perform the distortion process on the syntactic phase only, without changing the semantic interpretation of code, hence further separating distortion from interpretation.
Related Works. The most related work is [20], based on the seminal paper [19], where obfuscation was formalized by means of completeness and interpreter specialization. Giacobazzi et al. [20] provide precisely the theoretical bases for obfuscating programs by interpreter specialization, in order to force intensional properties affecting the precision of a given static analysis. With respect to [20], we focus the attention on what we want to protect rather than on what the attacker can observe/analyze. Moreover, Giacobazzi et al. [20] did not provide any systematic approach for deriving the distorted interpreters. Our aim is to fill the gap between the identification of the property to make obscure and the process for building the distorted interpreter to specialize for obscuring the property.
Dalla Preda and Mastroeni [16] exploit the relation between obfuscation and completeness to design property-driven obfuscation strategies as program transformations revealing (preserving) some fixed semantic property while concealing a property to protect. In this work, it is also shown that the obfuscation approach based on distorted interpreters [20] is precisely a technique for revealing the I/O program semantics while concealing a given property to protect. The problem with this work is that it still does not provide a constructive method for obfuscating programs, but only a theoretical framework for designing obfuscation strategies. Finally, Giacobazzi et al. [21] exploit the relation between completeness and obfuscation for “measuring” obfuscation potency, namely the obfuscator capability of hiding properties.
2 Background
2.1 The Language \({{\,\mathrm{{\mathfrak {L}}}\,}}\) and Control Flow Graphs
Following [5, 30] (see also [37]) we consider the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\) of regular commands in Fig. 1 (where + denotes non-deterministic choice and \(*\) is the Kleene closure), which is general enough to cover deterministic imperative languages. We complete the Bruni et al. grammar [5] with an expressions grammar, and we make some syntactic change in order to simplify the parsing and interpretation processes. In particular, we use ; not for composing statements (composition is made by concatenation of statements) but for delimiting the end of a statement. We use delimiters
 and
and
 for determining the action range of +, we use
for determining the action range of +, we use
 and
and
 for the range of \(*\), and we use
for the range of \(*\), and we use
 and
and
 for delimiting programs. Let \({{\,\mathrm{{\mathfrak {L}}}\,}}\) denote also the set of programs in the language and
for delimiting programs. Let \({{\,\mathrm{{\mathfrak {L}}}\,}}\) denote also the set of programs in the language and
 the set of all the variables in
the set of all the variables in
 .
.
Programs will be graphically represented by means of their control flow graphs (CFG for short). The definition is quite standard [33], but we recall it here in order to fix the notation we use. The CFG of
 is the labeled directed graph whose nodes are program points
is the labeled directed graph whose nodes are program points
 and whose edge labels are in the language \({L}_\texttt{sp}\ni \ \texttt{l}::=\ x:=\textsf{e}\mid \textbf{skip}\mid \texttt{b}\). In order to build the CFG, in the following, we will use labeled programs in \({{\,\mathrm{{\mathfrak {L}}}\,}}\), namely code in \({{\,\mathrm{{\mathfrak {L}}}\,}}\) where program points are labeled with values in a set of labels \({ Lab}\). The labels are not in the syntax since they can be considered as program annotations added by a labeling function. Formally, let
and whose edge labels are in the language \({L}_\texttt{sp}\ni \ \texttt{l}::=\ x:=\textsf{e}\mid \textbf{skip}\mid \texttt{b}\). In order to build the CFG, in the following, we will use labeled programs in \({{\,\mathrm{{\mathfrak {L}}}\,}}\), namely code in \({{\,\mathrm{{\mathfrak {L}}}\,}}\) where program points are labeled with values in a set of labels \({ Lab}\). The labels are not in the syntax since they can be considered as program annotations added by a labeling function. Formally, let
 its CFG is
its CFG is
 , where
, where
 is inductively defined on the structure of \(\texttt{C}\) (we ignore the initial and final brackets).
is inductively defined on the structure of \(\texttt{C}\) (we ignore the initial and final brackets).

The nodes can be restricted to those involved in edges, i.e., \({ Nodes}({{\texttt{Cfg}}}(\texttt{C}))=\{q~|~\exists \langle q,\texttt{l},q' \rangle \in {{\texttt{Cfg}}}(\texttt{C})\ {or}\ \langle q',\texttt{l},q \rangle \in {{\texttt{Cfg}}}(\texttt{C}),\ \texttt{l}\in {L}_\texttt{sp}\}\). In Fig. 2 we have, on the right, an example of CFG extracted from a simple program and on the left we have a simplified version, where all the true transitions are omitted and states are relabeled.
2.2 The Language Semantics
Denotations are memories, i.e., partial functions \({{\,\mathrm{\mathbb {m}}\,}}:{ Var}\longrightarrow \mathbb {V}\cup \{\$\}\in \mathbb {M}\) where \(\mathbb {V}\) is a domain of values, e.g.,
 and \(\$\) denotes an uninstantiated value. A memory assigns values in \(\mathbb {V}\) only to a finite set of variables, i.e., it is a variable finite memory [4]. We abuse notation by denoting as \(\mathbb {M}\) precisely the set of such memories. We define
and \(\$\) denotes an uninstantiated value. A memory assigns values in \(\mathbb {V}\) only to a finite set of variables, i.e., it is a variable finite memory [4]. We abuse notation by denoting as \(\mathbb {M}\) precisely the set of such memories. We define
 and for \(\textsf{M}\subseteq \mathbb {M}\), we define \({ var}(\textsf{M})=\bigcup _{{{\,\mathrm{\mathbb {m}}\,}}\in \textsf{M}}{ var}({{\,\mathrm{\mathbb {m}}\,}})\). As usual we will often represent a memory \({{\,\mathrm{\mathbb {m}}\,}}\in \mathbb {M}\) as a tuple \([x_1/v_1,\ldots ,x_n/v_n]\) of its defined variable/value pairs, i.e., such that \({{\,\mathrm{\mathbb {m}}\,}}(y)=\$\) if \(y\notin \{x_1,\ldots ,x_n\}\) and \({{\,\mathrm{\mathbb {m}}\,}}(y)=v_i\) if \(y=x_i\) for all \(i\in [1,n]\). Memory update is written \({{\,\mathrm{\mathbb {m}}\,}}[x\mapsto v]\) and it associates with x the value v, while all the other associations remain the same. The concrete semantics of the program can be computed by a fine-grain small-step execution deriving the set of all the possible executions of programs. In the following,
and for \(\textsf{M}\subseteq \mathbb {M}\), we define \({ var}(\textsf{M})=\bigcup _{{{\,\mathrm{\mathbb {m}}\,}}\in \textsf{M}}{ var}({{\,\mathrm{\mathbb {m}}\,}})\). As usual we will often represent a memory \({{\,\mathrm{\mathbb {m}}\,}}\in \mathbb {M}\) as a tuple \([x_1/v_1,\ldots ,x_n/v_n]\) of its defined variable/value pairs, i.e., such that \({{\,\mathrm{\mathbb {m}}\,}}(y)=\$\) if \(y\notin \{x_1,\ldots ,x_n\}\) and \({{\,\mathrm{\mathbb {m}}\,}}(y)=v_i\) if \(y=x_i\) for all \(i\in [1,n]\). Memory update is written \({{\,\mathrm{\mathbb {m}}\,}}[x\mapsto v]\) and it associates with x the value v, while all the other associations remain the same. The concrete semantics of the program can be computed by a fine-grain small-step execution deriving the set of all the possible executions of programs. In the following,
 denotes the set of the (terminating) program computations modeled as finite traces of memories [12], while \((\!|\textsf{e}|\!){{\,\mathrm{\mathbb {m}}\,}}\) denotes the concrete evaluation of \(\textsf{e}\in {{\,\textrm{Exp}\,}}\) in the memory \({{\,\mathrm{\mathbb {m}}\,}}\).
denotes the set of the (terminating) program computations modeled as finite traces of memories [12], while \((\!|\textsf{e}|\!){{\,\mathrm{\mathbb {m}}\,}}\) denotes the concrete evaluation of \(\textsf{e}\in {{\,\textrm{Exp}\,}}\) in the memory \({{\,\mathrm{\mathbb {m}}\,}}\).
The Collecting Semantics. The collecting big-step semantics of programs in \({{\,\mathrm{{\mathfrak {L}}}\,}}\) (denoted by the subscript \({\mathcal C}\)) is defined as the additive lift of the standard I/O semantics and it is inductively defined on program’s syntax. We first define the collecting semantics for \(\textsf{a}\in {{\,\textrm{AExp}\,}}\), \({\llbracket \textsf{a} \rrbracket }_{{ {\mathcal C}}}:\wp (\mathbb {M})\longrightarrow \wp (\mathbb {V})\), as additive lift to sets of memories:
 . Similarly, for boolean expressions \(\textsf{b}\in {{\,\textrm{BExp}\,}}\), \({\llbracket \textsf{b} \rrbracket }_{{ {\mathcal C}}}:\wp (\mathbb {M})\longrightarrow \wp (\mathbb {M})\) is defined as
. Similarly, for boolean expressions \(\textsf{b}\in {{\,\textrm{BExp}\,}}\), \({\llbracket \textsf{b} \rrbracket }_{{ {\mathcal C}}}:\wp (\mathbb {M})\longrightarrow \wp (\mathbb {M})\) is defined as
 . The semantics of
. The semantics of
 is
is
 defined inductively as follows [4]Footnote 1 where
defined inductively as follows [4]Footnote 1 where
 and
and
 :
:

Note that the collecting semantics of any non terminating program
 is
is
 . In this case, if \(\varnothing \) denotes the undefined memory, then
. In this case, if \(\varnothing \) denotes the undefined memory, then
 is the collection of memories computed by
is the collection of memories computed by
 .
.
In the following we will use also the notion of store, allowing us to locally denote collecting updates by associating, with each program point the collection of memories reached at each point. This allows to define a collecting small-step semantics abstracting
 [1, 12]. Let us define,
[1, 12]. Let us define,
 such that for any \({{\,\mathrm{\mathbb {s}}\,}}\in \mathbb {S}\) there exists a finite set of program labels \(q\in { Lab}\) such that \({{\,\mathrm{\mathbb {s}}\,}}(q)\ne \$ \), in particular, given a program
such that for any \({{\,\mathrm{\mathbb {s}}\,}}\in \mathbb {S}\) there exists a finite set of program labels \(q\in { Lab}\) such that \({{\,\mathrm{\mathbb {s}}\,}}(q)\ne \$ \), in particular, given a program
 we have that
we have that
 (when not necessary or when clear from the context, we will avoid the subscript
(when not necessary or when clear from the context, we will avoid the subscript
 ). In the following, we will denote by \({{\,\mathrm{\mathbb {s}}\,}}^{q}\) the set of memories associated with \(q\in { Lab}\), i.e., \({{\,\mathrm{\mathbb {s}}\,}}(q)\in \wp (\mathbb {M})\). For the sake of readability, we will also use the following update notation:
). In the following, we will denote by \({{\,\mathrm{\mathbb {s}}\,}}^{q}\) the set of memories associated with \(q\in { Lab}\), i.e., \({{\,\mathrm{\mathbb {s}}\,}}(q)\in \wp (\mathbb {M})\). For the sake of readability, we will also use the following update notation:
 if \(q=q'\), \({{\,\mathrm{\mathbb {s}}\,}}(q')\) otherwise. Moreover, we will denote by \({{\,\mathrm{\mathbb {s}}\,}}_{\varnothing }\) the store mapping each program point to the emptyset, i.e., \(\forall q.\,{{\,\mathrm{\mathbb {s}}\,}}_{\varnothing }(q)=\varnothing \).
if \(q=q'\), \({{\,\mathrm{\mathbb {s}}\,}}(q')\) otherwise. Moreover, we will denote by \({{\,\mathrm{\mathbb {s}}\,}}_{\varnothing }\) the store mapping each program point to the emptyset, i.e., \(\forall q.\,{{\,\mathrm{\mathbb {s}}\,}}_{\varnothing }(q)=\varnothing \).
The Abstract Semantics. The abstract semantics of programs is an abstraction of the concrete small-step semantics [12,13,14], also called trace semantics. An abstract domain is a set of properties, here modeled as upper closure operators (uco for short), i.e., a monotone, extensive and idempotent operator on \(\wp (\mathbb {M})\) [14]. If \({\mathcal A}\in { uco}(\wp (\mathbb {M}^*))\) is an abstraction of program traces, then we can denote by
 the fix-point computation (inductively defined on the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\)) as the \(\mathcal {A}\) observation of
the fix-point computation (inductively defined on the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\)) as the \(\mathcal {A}\) observation of
 . In static analysis, it is quite common to define the semantic abstraction in terms of an abstraction of variable values \(\mathbb {V}\). In general, if a program has n variables, then concrete values for the program are n-tuples of values. Hence, abstract domains must be parametric on the number n of variables of the program to analyze, i.e., we have to consider, as abstract domains, families of abstractions \(\{\rho _n\in { uco}(\wp (\mathbb {V}^n))\}_{n\in \mathbb {N}}\) [4, 15]. For the sake of readability, in the following we simply denote this family of abstraction as \(\rho \), ignoring the technical aspect that it changes with the number of variables of the program to analyze, and we denote the corresponding abstract semantics as
. In static analysis, it is quite common to define the semantic abstraction in terms of an abstraction of variable values \(\mathbb {V}\). In general, if a program has n variables, then concrete values for the program are n-tuples of values. Hence, abstract domains must be parametric on the number n of variables of the program to analyze, i.e., we have to consider, as abstract domains, families of abstractions \(\{\rho _n\in { uco}(\wp (\mathbb {V}^n))\}_{n\in \mathbb {N}}\) [4, 15]. For the sake of readability, in the following we simply denote this family of abstraction as \(\rho \), ignoring the technical aspect that it changes with the number of variables of the program to analyze, and we denote the corresponding abstract semantics as
 . Given a value abstraction \(\rho \), we can define a memory abstraction, abstracting sets of memories in \(\mathbb {M}\) in abstract memories in \(\mathbb {M}^{\rho }\). Define the memory abstraction as the tuple \(\mathcal {A}_\rho =\langle \rho ,\mathbb {M}^{\rho },\alpha _\rho ,\gamma _\rho \rangle \), where we define \({\alpha _{\rho }:\wp (\mathbb {M})\rightarrow \mathbb {M}^{\rho }}\) (
. Given a value abstraction \(\rho \), we can define a memory abstraction, abstracting sets of memories in \(\mathbb {M}\) in abstract memories in \(\mathbb {M}^{\rho }\). Define the memory abstraction as the tuple \(\mathcal {A}_\rho =\langle \rho ,\mathbb {M}^{\rho },\alpha _\rho ,\gamma _\rho \rangle \), where we define \({\alpha _{\rho }:\wp (\mathbb {M})\rightarrow \mathbb {M}^{\rho }}\) (
 ), while the concretization is the function \({\gamma _\rho :\mathbb {M}^{\rho }\rightarrow \wp (\mathbb {M})}\) (defined on abstract collecting memories as
), while the concretization is the function \({\gamma _\rho :\mathbb {M}^{\rho }\rightarrow \wp (\mathbb {M})}\) (defined on abstract collecting memories as
 ).
).
In order to define the abstract semantics, we define the semantics of expressions \({\llbracket \textsf{e} \rrbracket }^{\rho }\) computing abstract operations in \(\rho \), and then we define the abstract semantics of basic instructions: Let \(\{x_i\}_{i\in I}\) be the set of defined variables ranging over i in the set of indexes \(I=[1,n]\).

In the assignment, we consider all the tuples where the potential relation among all the variables different from \(x_i\) remains unaltered, while \(x_i\) may have any value in \({\llbracket \textsf{e} \rrbracket }^{\rho }\overline{\textsf{M}}\). The abstract semantics, of a program
 , is simply denoted as
, is simply denoted as
 and it is inductively defined on the syntax of commands (loops, conditionals and compositions) as the composition of the abstract semantics of their components [4]. It is well known that abstract interpretation is not compositional, namely the composition of two best correct approximation (bca for short) semantics is not the bca semantics of the composition. This is indeed the main source of imprecision in program analysis. Note that, also for abstract semantics we can use (abstract) stores \(\mathbb {S}^{\rho }\) for defining abstract collecting rules where we associate with program points abstract memories in \(\mathbb {M}^{\rho }\).
and it is inductively defined on the syntax of commands (loops, conditionals and compositions) as the composition of the abstract semantics of their components [4]. It is well known that abstract interpretation is not compositional, namely the composition of two best correct approximation (bca for short) semantics is not the bca semantics of the composition. This is indeed the main source of imprecision in program analysis. Note that, also for abstract semantics we can use (abstract) stores \(\mathbb {S}^{\rho }\) for defining abstract collecting rules where we associate with program points abstract memories in \(\mathbb {M}^{\rho }\).
Program Specialization. Program specialization is a source-to-source program transformation also known as partial evaluation [26]. A specializer is a program \(\texttt{spec}\) such that for
 with “static” input \(\texttt{s}\in D\) and “dynamic” input \(\texttt{d}\in D\)
with “static” input \(\texttt{s}\in D\) and “dynamic” input \(\texttt{d}\in D\)
 where \({\mathcal S}[\cdot ]\) denotes generic semantics associating I/O meaning to programs independently from the language, hence distinguishing the I/O semantics from the collecting semantics \({\llbracket \cdot \rrbracket }_{{ {\mathcal C}}}\). A specializer executes
where \({\mathcal S}[\cdot ]\) denotes generic semantics associating I/O meaning to programs independently from the language, hence distinguishing the I/O semantics from the collecting semantics \({\llbracket \cdot \rrbracket }_{{ {\mathcal C}}}\). A specializer executes
 in two stages: (1)
in two stages: (1)
 is specialized to its static input \(\texttt{s}\) yielding a “residual program”
is specialized to its static input \(\texttt{s}\) yielding a “residual program”
 , (2)
, (2)
 can be run on
can be run on
 ’s dynamic input \(\texttt{d}\) [26].
’s dynamic input \(\texttt{d}\) [26].
A trivial specializer \(\texttt{spec}\) is easy to build by “freezing” the static input \(\texttt{s}\) (Kleene’s s-m-n Theorem of the 1930s s did specialization in this way.) A number of practical program specializers exist. Published partial evaluation systems include Tempo, Ecce, Logen, Unmix, Similix and PGG [11, 28, 29, 32, 34].
3 Symbolic Finite State Machines
In this section, we define a generic notion of symbolic machine and symbolic transducer by generalizing the symbolic automata and transducers defined in the literature [17, 35]. The idea consists in generalizing the symbolic approach (admitting potentially infinite alphabets) also to finite state machines/transducers equivalent to Turing Machines, namely with more than one stack and/or with writable input tape, while simplifying the notation, for instance by avoiding to introduce a further notion of interpretation for symbols. The following machines are non deterministic with \(\varepsilon \) transitions, where as usual \(\varepsilon \) is a special symbol used for executing transitions without reading symbols.
3.1 Finite State Machines
By finite state machines we mean any state machine with a finite number of states that reads an input sequence of symbols. Each symbol allows the execution of a transition, and final states decide which input sequences are accepted by the machine, accepted when the input reading leads to a final state. The notion is recalled only because we provide a unique parametric definition for automata and Turing machines.
Definition 1 (Finite state machines (FSM))
A FSM is the tuple \(M=\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varSigma , \varGamma , \texttt{S},\delta \rangle \) where
-
\(\mathbb {Q}\) is a finite set of states (\(q_\iota \in \mathbb {Q}\) initial state, \(q_{\texttt{f}}\in \mathbb {Q}\) final/accepting state)Footnote 2;
-
\(\varSigma \) and \(\varGamma \) are finite input and stack alphabets, respectively;
-
\(\texttt{S}\subseteq \{{ Stack}^n\}\cup \{{ Input}\}\) is a set of tapes which may contain \(n\ge 0\) \({ Stack}\)s (if \(n=0\) there are no stacks), i.e., LIFO tapes, and one
 tape, a writable and readable input tape where we can stop or move left/rightFootnote 3;
tape, a writable and readable input tape where we can stop or move left/rightFootnote 3; -
\(\delta :\mathbb {Q}\times \varSigma \times \varGamma ^n\rightarrow \wp (\mathbb {Q})\times \{R,L,H\}^{\{0,1\}}\times (\varGamma ^*)^n\) is the transition function. The transition \(q\rightarrow q'\) labeled with \(((s,M),\{t_i\rightarrow \gamma _i\}_{i\in [1,n]})\) (read \(s\in \varSigma \) in the state q with the top (popped) elements of the stacks \(\{t_i\}_{i\in [1,n]}\), reach \(q'\), push \(\{\gamma _i\}_{i\in [1,n]}\) on the n stacks, and move \(M\in \{R,L,H\}\))Footnote 4 iff \(\langle q',M,\{\gamma _i\}_{i\in [1,n]} \rangle \in \delta (q,s,\{t_i\}_{i\in [1,n]})\).
In order to make such a machine symbolic, we simply consider infinite alphabets (both for input and stack) and a recursive enumerable set of decidable predicates on the alphabet symbols. In this way, transitions are labeled with predicates allowing all the symbols satisfying the property to be read in the transition (on the input tape or on the stack).
Definition 2 (Symbolic finite state machines (SFSM))
A SFSM is the tuple \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varPsi _\varSigma ,\varPsi _\varGamma , \texttt{S}, \delta \rangle \) where
-
\(\mathbb {Q}\) is a finite set of states (\(q_\iota \in \mathbb {Q}\) initial state, \(q_{\texttt{f}}\in \mathbb {Q}\) final/accepting state);
-
\(\varSigma \) and \(\varGamma \) are infinite input and stack alphabets, respectively;
-
\(\varPsi _\varSigma \subseteq \wp (\varSigma )\) and \(\varPsi _\varGamma \subseteq \wp (\varGamma )\) are recursive enumerable sets of predicates on \(\varSigma \) and \(\varGamma \) (closed under logic connectives)Footnote 5;
-
 (\(n\ge 0\) number of stacks);
(\(n\ge 0\) number of stacks); -
\(\delta :\mathbb {Q}\times \varPsi _\varSigma \times (\varPsi _\varGamma )^n\rightarrow \wp (\mathbb {Q})\times \{R,L,H\}^{\{0,1\}}\times (\varGamma ^*)^n\), where we have the transition \(q\rightarrow q'\) labeled with \(((s,M),\{t_i\rightarrow \gamma _i\}_{i\in [1,n]})\) iff
 ,
,
 , \(\gamma \in \varGamma ^n\) and \(M\in \{R,L,H\}\) such that
, \(\gamma \in \varGamma ^n\) and \(M\in \{R,L,H\}\) such that
 , with
, with
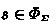 and
and
 .
.
3.2 Finite State Transducers
Finite state transducers are finite state machine providing an output sequence of symbols for each transition. The standard generalized notion is the following.
Definition 3 (Finite state transducers (FST))
A finite state transducer is a FSM with an output language, i.e., a tuple \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varSigma , \varGamma , \texttt{S},\tilde{\delta },\varOmega \rangle \), where \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varSigma , \varGamma , \texttt{S},\delta \rangle \) is a FSM, \(\varOmega \) is a finite output alphabet, and the transition function \(\tilde{\delta }:\mathbb {Q}\times \varSigma \times \varGamma ^n\rightarrow \wp (\mathbb {Q})\times \{R,L,H\}^{\{0,1\}}\times (\varGamma ^*)^n\times \varOmega ^*\) is \(\delta \) extended by returning also an output string \(\omega \in \varOmega ^*\) for each input symbol read, i.e.,
 .
.
In this case, we have the transition \(q\rightarrow q'\) labeled with
 (read \(s\in \varSigma \) in the state q with the top (popped) elements of the i-th stack
(read \(s\in \varSigma \) in the state q with the top (popped) elements of the i-th stack
 ) and reach state \(q'\), push
) and reach state \(q'\), push
 on the i-th stack (\(i\in [1,n]\)), move M and provide in output the sequence \(\omega \in \varOmega \)) iff
on the i-th stack (\(i\in [1,n]\)), move M and provide in output the sequence \(\omega \in \varOmega \)) iff
 , and therefore
, and therefore
 .
.
In the symbolic extension, following the Veanes et al. [35], we simply consider a function that for each input symbol read, provides a sequence of output symbols.
Definition 4 (Symbolic finite state transducers (SFST))
A symbolic finite state transducers is a SFSM with an output language, i.e., it is defined as a tuple \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}}, \varPsi _\varSigma ,\varPsi _\varGamma , \texttt{S},\tilde{\delta },\varOmega ,\texttt{f} \rangle \), where \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}}, \varPsi _\varSigma ,\varPsi _\varGamma , \texttt{S},\delta \rangle \) is a SFSM, \(\varOmega \) is an infinite output alphabet, \(\texttt{f}:\varSigma \rightarrow \varOmega ^*\), and the transition function \(\tilde{\delta }\) is defined as \(\langle \delta ,\texttt{f} \rangle \).
In this case, we have the transition
 labeled with
labeled with
 (read
(read
 in the state
in the state
 with the top (popped) elements of the i-th stack
with the top (popped) elements of the i-th stack
 (
(
 ) and reach state \(q'\), push
) and reach state \(q'\), push
 (
(
 ), move M and provide in output the symbols
), move M and provide in output the symbols
 ) iff
) iff
 and
and
 ,
,
 .
.
When dealing with symbolic transducers we can characterize the corresponding transduction function.
Definition 5 (Transduction)
[35] The transduction of a symbolic transducer \(\texttt{T}\) is the function \({\mathfrak {T}}_{\texttt{T}}:\varSigma ^*\rightarrow \wp (\varOmega ^*)\) where
 Footnote 6.
Footnote 6.
Note that a symbolic machine
 can be always transformed in the transducer
can be always transformed in the transducer
 , where the output language is precisely the input one.
, where the output language is precisely the input one.
We can compose transducers
 and
and
 by composing their transductions [35]
by composing their transductions [35]
 and
and
 as:
as:

3.3 Example: Parser as Symbolic Pushdown Automaton
Being the language generated by a context free grammar, the parser can be modeled as a symbolic pushdown (non deterministic) automaton. In particular, it is the automaton
 , where
, where
-
 ;
; -

 ;
; -
 ;
; -
 and \(\varPsi _\varGamma =\left\{ ~\{t\} \left| \begin{array}{l}t\in \varGamma \end{array} \right. \right\} \)Footnote 7;
and \(\varPsi _\varGamma =\left\{ ~\{t\} \left| \begin{array}{l}t\in \varGamma \end{array} \right. \right\} \)Footnote 7; -
 is graphically defined in Fig. 3, where each transition is labeled with \((s\in \phi ,t\rightarrow \gamma )\), meaning that \(\phi \) is a predicate on \(\varSigma \) and \(s\in \phi \), while from the stack we pop
is graphically defined in Fig. 3, where each transition is labeled with \((s\in \phi ,t\rightarrow \gamma )\), meaning that \(\phi \) is a predicate on \(\varSigma \) and \(s\in \phi \), while from the stack we pop
 (\(t=\varepsilon \) means that we don’t pop anything from the stack) and we push \(\gamma \in \varGamma ^*\)Footnote 8.
(\(t=\varepsilon \) means that we don’t pop anything from the stack) and we push \(\gamma \in \varGamma ^*\)Footnote 8.
This parser simply checks brackets balance, where \(+\) (\(*\)) is pushed whenever a bracket is opened, and the same symbol is popped when it is closed. We can terminate only if the stack is empty (when on the top there is
 ).
).
4 Program (Re)Interpretation
As usual the interpretation of programs is specified in two phases: The parsing phase of programs, where programs are viewed as sequences of statements, and the semantic interpretation phase, i.e., the corresponding transformation of memories/stores. The first phase is modeled as symbolic Turing Machine reading in input the sequence of symbols corresponding to the program syntax, and providing in output the precise sequences of single statements (skip and assignments) to execute and of guards to evaluate. This resulting set of sequences corresponds indeed to the CFG of the program, and on this structure we can perform the semantic interpretation phase, whose rule definitions are indeed independent from the sequence of statements/guards to execute/evaluate. Indeed, such semantic interpretation phase may be defined on concrete memories, on collecting memories of even on abstract memories, without affecting the computation of the previous interpretation phase.
4.1 First Phase: The Execution Sequence Extractor
The parsing of the input program, aiming also at extracting the sequence of executed statements and evaluated guards, is modeled as a symbolic Turing machine equipped with a stack. It should be clear that the input language is the language of the parser \(\texttt{pars}\), that is indeed embedded in the interpreter. Hence the first component is

-
 ;
; -
 and
and
 ;
; -
 ;
; -
 ;
; -
 graphically defined in Fig. 4 together with \(\texttt{f}:\varSigma \rightarrow \varOmega \), where each transition is labeled, as described before, with
graphically defined in Fig. 4 together with \(\texttt{f}:\varSigma \rightarrow \varOmega \), where each transition is labeled, as described before, with
 .
.
In particular, \(q_2\) handles the single statement execution or the guard evaluation. \(q_3\) handles the non deterministic choice. In particular it moves to \(q_1\) for executing the statement on the left of + (and when it finds the symbol + it skips, in \(q_4\), what remains up to the closed parenthesis
 ). \(q_3\) moves to \(q_4\) if it wants to execute the statements on the right of +. In this case it skips all the statements up to + again in \(q_4\). We use the stack for recognizing nested +. State \(q_7\) handles loops, in particular it moves to \(q_1\) for executing the body (the statements between
). \(q_3\) moves to \(q_4\) if it wants to execute the statements on the right of +. In this case it skips all the statements up to + again in \(q_4\). We use the stack for recognizing nested +. State \(q_7\) handles loops, in particular it moves to \(q_1\) for executing the body (the statements between
 and
and
 ). In this case when we read
). In this case when we read
 it moves to \(q_6\) for returning back at the beginning of the loop. \(q_7\) moves to \(q_8\) for skipping the loop, by looking for
it moves to \(q_6\) for returning back at the beginning of the loop. \(q_7\) moves to \(q_8\) for skipping the loop, by looking for
 and continuing the execution.
and continuing the execution.
In this way, if the input is a legal program, then it is accepted and the output sequences are the sequences of statements to execute and of guards to evaluate. We can observe that if we keep also the graph structure of the output (intuitively, ignoring
 -transitions and collapsing states recognizing the same language), then we obtain a graph equivalent to the CFG of the program.
-transitions and collapsing states recognizing the same language), then we obtain a graph equivalent to the CFG of the program.
Definition 6 (Partial interpreter evaluation)
The partial interpreter evaluation is the sequence/trace of statements/expressions to actually execute for a given program. Formally, given
 and the execution sequence extractor
and the execution sequence extractor
 , \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varPsi _\varSigma ,\varPsi _\varGamma \{{ Stack},{ Input}\},\tilde{\delta },\varOmega ,\texttt{f} \rangle \) (
, \(\langle \mathbb {Q},q_\iota ,q_{\texttt{f}},\varPsi _\varSigma ,\varPsi _\varGamma \{{ Stack},{ Input}\},\tilde{\delta },\varOmega ,\texttt{f} \rangle \) (
 ), the partial evaluation of
), the partial evaluation of
 is
is
 .
.
Let us denote
 the automaton recognizing the output language
the automaton recognizing the output language
 of \(\texttt{cfgEx}\) transduction of the input sequence
of \(\texttt{cfgEx}\) transduction of the input sequence
 . Then we can observe that
. Then we can observe that
 corresponds to the CFG (seen as SFSM) of
corresponds to the CFG (seen as SFSM) of
 , i.e.,
, i.e.,
 (up to label renaming and minimization). Note that
(up to label renaming and minimization). Note that
 is a FSM (no more symbolic), (the one of the statements in
is a FSM (no more symbolic), (the one of the statements in
 ) of the infinite
) of the infinite
 . Let us show this correspondence on some examples.
. Let us show this correspondence on some examples.
Example 1
Consider the program
 ,
,

In the picture we depict the whole path of interpretation by means of the given interpreter: We obtain so far the automaton
 generated by the transduction of the interpreter on
generated by the transduction of the interpreter on
 . Each transition is labeled with \(((s/o,M),t\rightarrow \gamma )\) meaning that we read s in input and we pop t from the stack, while we move M we output \(\omega \) and we push \(\gamma \) on the stack.
. Each transition is labeled with \(((s/o,M),t\rightarrow \gamma )\) meaning that we read s in input and we pop t from the stack, while we move M we output \(\omega \) and we push \(\gamma \) on the stack.

If we transitively collect the transitions with output \(\varepsilon \) and we collapse states recognizing the same language, while keeping the branch and the final states, we obtain the graph on the left of Fig. 5, which corresponds to the CFG of
 .
.
Consider now the program


the graph in the center of Fig. 5 corresponds to the automaton
 , where the labels are the output symbols. Finally, consider the program
, where the labels are the output symbols. Finally, consider the program


The graph on the right of Fig. 5 corresponds to
 , where the labels are the output symbols.
, where the labels are the output symbols.
4.2 Second Phase: The Semantic Interpretation
The semantic interpretation is just an interpretation function depending on the domain of denotations, and defined for each element of
 , the output symbols to interpret. In general, given a graph
, the output symbols to interpret. In general, given a graph
 , with initial state
, with initial state
 whose labels are in the language
whose labels are in the language
 , and given a semantic rule system
, and given a semantic rule system
 defining the small-step semantics for
defining the small-step semantics for
 , namely determining how semantic denotations in
, namely determining how semantic denotations in
 (e.g., stores in
(e.g., stores in
 ) are transformed by the execution of elements in
) are transformed by the execution of elements in
 , we can interpret its paths on denotations
, we can interpret its paths on denotations
 by using the following function on set of graph configurations
by using the following function on set of graph configurations
 , let
, let
 ,
,
 and
and


where
 denotes the least upper bound on
denotes the least upper bound on
 . Then, we can compute the fix-point interpretation of the graph
. Then, we can compute the fix-point interpretation of the graph
 , starting from an initial denotation
, starting from an initial denotation
 as the least fix-pointFootnote 9 of the extensive version of
as the least fix-pointFootnote 9 of the extensive version of
 , i.e.,
, i.e.,
 , defined in terms of the semantic rule system
, defined in terms of the semantic rule system
 . This fix-point computes the set of all the reachable configurations, hence in order to extract the final/terminating ones, we have simply to consider, in this fix-point, only the configurations in
. This fix-point computes the set of all the reachable configurations, hence in order to extract the final/terminating ones, we have simply to consider, in this fix-point, only the configurations in
 .
.

For instance, in order to define a collecting small-step semantics we have to define a collecting rule system
 interpreting
interpreting
 (Table 1) on stores
(Table 1) on stores
 , where, given the set of initial memories
, where, given the set of initial memories
 , the initial store is
, the initial store is
 ,
,
 , also denoted
, also denoted
 , Note that, the interpretation of
, Note that, the interpretation of
 is simply like interpreting
is simply like interpreting
 , and for this reason it is simply ignored.
, and for this reason it is simply ignored.
Then the graph
 collecting semantic interpretation is the following, where being interested only in the memories reached at the end of the program execution, we consider only the store memories at the final point
collecting semantic interpretation is the following, where being interested only in the memories reached at the end of the program execution, we consider only the store memories at the final point
 .
.

As observed before, when we consider an abstract semantics
 Footnote 10 we obtain an abstract interpreter. The idea is simple, we can define a rule system
Footnote 10 we obtain an abstract interpreter. The idea is simple, we can define a rule system
 which is precisely
which is precisely
 where the abstract semantics
where the abstract semantics
 for interpreting expressions is used instead of
for interpreting expressions is used instead of
 , and in terms of which we obtain, as before, a corresponding interpretation function
, and in terms of which we obtain, as before, a corresponding interpretation function
 . Then we can define
. Then we can define

4.3 Interpreting Programs
Finally we can compose the two phases and obtain the characterization of interpretation for programs
 . In particular, as observed in the previous section,
. In particular, as observed in the previous section,
 returns precisely a graph with
returns precisely a graph with
 as label’s language, hence we can use the above semantic interpretation on this resulting graph.
as label’s language, hence we can use the above semantic interpretation on this resulting graph.
Definition 7 (Program interpreter)
Given a semantic rule system
 for
for
 and
and
 inductively defined on its labels in \({L}_\texttt{sp}\). A program interpreter for the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\) is the pair
inductively defined on its labels in \({L}_\texttt{sp}\). A program interpreter for the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\) is the pair
 . Hence,
. Hence,
 the program interpretation is
the program interpretation is
 .
.
For instance, the collecting interpreter for
 is
is
 , while an abstract interpreter w.r.t. the variable values abstraction
, while an abstract interpreter w.r.t. the variable values abstraction
 is
is
 .
.
Combining all together, given
 , its collecting semantics starting from initial memories
, its collecting semantics starting from initial memories
 is computed as follows. The following result holds by construction and by the intuitive equivalence between the collecting program semantics and the collecting interpretation of its CFG.
is computed as follows. The following result holds by construction and by the intuitive equivalence between the collecting program semantics and the collecting interpretation of its CFG.
Proposition 1
Let
 , then we have
, then we have
 , where by construction
, where by construction
 . In the abstract case,
. In the abstract case,
 , where
, where
 .
.
4.4 Specializing Interpreters
In classical computational theory [31] the interpreter is indeed a program with two inputs, a fragment of code to execute and the set of initial memories from which to start execution. Our model of program interpretation distinguishes precisely between the application to the first input (the program) and the second input (the initial memories). In particular, the first phase consists precisely in applying the interpreter to the program, and the second phase consists in applying the resulting structure to the set of initial memories. In other words, it should be clear that the simple transduction
 is precisely the specialization of the interpreter on the program, precomputing the interpretation computation involving only the code, namely the characterization of the sequences of statements to execute and of guards to evaluate. This corresponds precisely to design the program CFG. The only interpretation steps that remain to perform are those concerning the semantic interpretation, depending also on data (formally on initial memories). Hence, we can write
is precisely the specialization of the interpreter on the program, precomputing the interpretation computation involving only the code, namely the characterization of the sequences of statements to execute and of guards to evaluate. This corresponds precisely to design the program CFG. The only interpretation steps that remain to perform are those concerning the semantic interpretation, depending also on data (formally on initial memories). Hence, we can write

Which is indeed a specializer because by construction we have:

5 Specializer (Dis)Optimality
In this section, we formally introduce specializer optimality, i.e., the specializer property characterizing the analysis precision.
5.1 Abstract Jones Optimality and Completeness
We consider code specialization in the specific context of the specialization of interpreters and abstract interpretation. Let
 be a semantic abstraction and let \(\texttt{int}\) be an interpreter. Note that, given the new definition of interpreter, a semantic abstraction could be both an approximation of the CFG, providing a CFG containing the concrete computations and/or an abstraction of data manipulated by programs. The following definition reinterprets the notion of Jones optimality where computation time is replaced by the precision of an abstract interpreter.
be a semantic abstraction and let \(\texttt{int}\) be an interpreter. Note that, given the new definition of interpreter, a semantic abstraction could be both an approximation of the CFG, providing a CFG containing the concrete computations and/or an abstraction of data manipulated by programs. The following definition reinterprets the notion of Jones optimality where computation time is replaced by the precision of an abstract interpreter.
Definition 8
(\(\mathcal {A}\)-optimality). A specializer \(\texttt{spec}\), implementing the function \({ spec}\), is \(\mathcal {A}\)-optimal w.r.t the interpreter \(\texttt{int}\) if it does not lose precision w.r.t. the semantic abstraction \(\mathcal {A}\), i.e., if
 .
.
Note that, if we replace
 with time complexity of P, this definition boils down precisely to Jones-optimality [25, 27]. When applied to the case of abstract interpretation, a stronger property is also important, as specified in the following definition.
with time complexity of P, this definition boils down precisely to Jones-optimality [25, 27]. When applied to the case of abstract interpretation, a stronger property is also important, as specified in the following definition.
Definition 9
(
 -suboptimality). A specializer \(\texttt{spec}\) implementing the function \({ spec}\) is \(\mathcal {A}\)-suboptimal w.r.t. an interpreter \(\texttt{int}\) if it does not add precision, i.e.,
-suboptimality). A specializer \(\texttt{spec}\) implementing the function \({ spec}\) is \(\mathcal {A}\)-suboptimal w.r.t. an interpreter \(\texttt{int}\) if it does not add precision, i.e.,
 .
.
While for straightforward abstractions
 , such as the identity and the top abstraction,
, such as the identity and the top abstraction,
 -suboptimality always holds, for non-straightforward abstractions
-suboptimality always holds, for non-straightforward abstractions
 ,
,
 -suboptimality depends upon the specializer
-suboptimality depends upon the specializer
 and the interpreter
and the interpreter
 .
.
Proposition 2
Given a self-interpreter (written in the interpreted language) \(\texttt{int}\), there exists an \(\mathcal {A}\)-(sub)optimal specializer.
Proof
The idea is similar to the case of trivial Jones-optimal [25]. Being \(\texttt{int}\) a self interpreter, there exists a trivial \(\mathcal {A}\)-optimal specializer semantics \(\overline{{ spec}}\), i.e.,

which is a (computable) specializer semantics, since
 .
.
Note that, when
 is not
is not
 -optimal, it may happen that we don’t have any relation between the original program and the specialized one, or it may happen that the specialized program is indeed less precise. In this case, namely when
-optimal, it may happen that we don’t have any relation between the original program and the specialized one, or it may happen that the specialized program is indeed less precise. In this case, namely when
 , then we say that
, then we say that
 , implementing the function
, implementing the function
 , is
, is
 -disoptimal w.r.t. the interpreter
-disoptimal w.r.t. the interpreter
 . Note that, both the notions of optimality and disoptimality may happen on a specific program, in particular we can say that
. Note that, both the notions of optimality and disoptimality may happen on a specific program, in particular we can say that
 is
is
 -suboptimal/optimal/disoptimal w.r.t. the interpreter \(\texttt{int}\) for the program
-suboptimal/optimal/disoptimal w.r.t. the interpreter \(\texttt{int}\) for the program
 if the corresponding definition holds for
if the corresponding definition holds for
 , i.e.,
, i.e.,
 .
.
Let us show the relation of optimality with precision in the abstract analysis, namely w.r.t completeness. Completeness in abstract interpretation means that the abstract computation
 is precise as the abstraction of the concrete computation, i.e.,
is precise as the abstraction of the concrete computation, i.e.,
 [14, 22]. In this case we say that
[14, 22]. In this case we say that
 is complete, while, if it holds for a program
is complete, while, if it holds for a program
 , we say that
, we say that
 is complete for
is complete for
 .
.
Lemma 1
Let
 be a (concrete) specializer implementing
be a (concrete) specializer implementing
 , \(\texttt{int}\) a collecting self interpreter and \(\mathcal {A}\) a semantic abstraction. Let
, \(\texttt{int}\) a collecting self interpreter and \(\mathcal {A}\) a semantic abstraction. Let
 , then we have the following facts:
, then we have the following facts:
-
1.

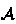 -suboptimal w.r.t. \(\texttt{int}\) \(\Rightarrow \)
-suboptimal w.r.t. \(\texttt{int}\) \(\Rightarrow \)
 (
(
 complete for \(\textsf{P}\) \(\Leftrightarrow \) \(\mathcal {A}\) complete for
complete for \(\textsf{P}\) \(\Leftrightarrow \) \(\mathcal {A}\) complete for
 );
); -
2.
 (
(
 complete for \(\textsf{P}\) and
complete for \(\textsf{P}\) and


 \(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
\(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
 );
); -
3.
 \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) \(\Rightarrow \)
\(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) \(\Rightarrow \)
 (
(
 complete for
complete for
 \(\Rightarrow \)
\(\Rightarrow \)
 complete for
complete for
 );
); -
4.
 (
(
 complete for
complete for
 \(\Rightarrow \)
\(\Rightarrow \)
 \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and
\(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and
 ).
).
Proof
Let us recall that, by construction
 .
.
-
1.
If \(\texttt{spec}\) is \(\mathcal {A}\)-suboptimal then
 . Suppose \(\mathcal {A}\) complete for
. Suppose \(\mathcal {A}\) complete for
 , then it means that
, then it means that
 , therefore we have
, therefore we have
 hence we have completeness also for
hence we have completeness also for
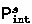 Analogously we can prove completeness for
Analogously we can prove completeness for
 when we have completeness for
when we have completeness for
 Intuitively, we have not the inverse implication since when \({\mathcal A}\) is both incomplete for
Intuitively, we have not the inverse implication since when \({\mathcal A}\) is both incomplete for
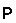 and
and
 we cannot imply anything on the optimality of the specializer, while when it is complete for both we can prove the following result.
we cannot imply anything on the optimality of the specializer, while when it is complete for both we can prove the following result. -
2.
If
 is complete for both
is complete for both
 and
and
 then
then
 and
and
 Therefore
Therefore
 meaning suboptimality w.r.t.
meaning suboptimality w.r.t.
 and
and

-
3.
If \(\texttt{spec}\) is \(\mathcal {A}\)-optimal then
 Suppose \(\mathcal {A}\) complete for
Suppose \(\mathcal {A}\) complete for
 , then it means that
, then it means that
 therefore we have
therefore we have
 Hence they are all equalities, and therefore we have completeness of
Hence they are all equalities, and therefore we have completeness of

-
4.
If, given
 , we have \(\mathcal {A}\) complete for
, we have \(\mathcal {A}\) complete for
 then
then
 hence we have
hence we have
 .
.
Theorem 1
Let \(\texttt{spec}\) be a (concrete) specializer implementing
 , \(\texttt{int}\) a collecting interpreter and \(\mathcal {A}\) a semantic abstraction. Let
, \(\texttt{int}\) a collecting interpreter and \(\mathcal {A}\) a semantic abstraction. Let
 , then we have that
, then we have that
 if \({\mathcal A}\) complete for \(\textsf{P}\) then: \({ spec}\) \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and \(\textsf{P}\) \(\Leftrightarrow \) \({\mathcal A}\) complete for
if \({\mathcal A}\) complete for \(\textsf{P}\) then: \({ spec}\) \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and \(\textsf{P}\) \(\Leftrightarrow \) \({\mathcal A}\) complete for
 \(\Leftrightarrow \) \({ spec}\) \(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
\(\Leftrightarrow \) \({ spec}\) \(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
 .
.
Proof
Trivial by Lemma 1. In particular, if
 is \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and
is \(\mathcal {A}\)-optimal w.r.t. \(\texttt{int}\) and
 , then by the hypothesis of completeness on P and by Lemma 1(3) we have \({\mathcal A}\) is complete for
, then by the hypothesis of completeness on P and by Lemma 1(3) we have \({\mathcal A}\) is complete for
 , and by Lemma 1(4) we have
, and by Lemma 1(4) we have
 \(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
\(\mathcal {A}\)-suboptimal w.r.t. \(\texttt{int}\) and
 . Finally, by definition
. Finally, by definition
 \(\mathcal {A}\)-suboptimal is also \(\mathcal {A}\)-optimal.
\(\mathcal {A}\)-suboptimal is also \(\mathcal {A}\)-optimal.
These results tell us that in order to obtain an obfuscator by specializing an interpreter we have to use a specializer which is not optimal w.r.t. the observation and the interpreter.
We now formalize the relation between the specializer optimality, w.r.t., a given interpreter, and our capability of obfuscating the source program by specializing an interpreter. Our aim is to exploit this relation for driving the distortion of the interpreter by means of the property we have to obfuscate, namely by the property to hide from the analyzer.
Theorem 2
Given an interpreter \(\texttt{int}\) and a specializer \(\texttt{spec}\) (with semantics
 ), we define the program transformer
), we define the program transformer
 . For any program
. For any program
 ,
,
 is an obfuscation of
is an obfuscation of
 w.r.t. the semantic abstraction \(\mathcal {A}\) iff
w.r.t. the semantic abstraction \(\mathcal {A}\) iff
 is \(\mathcal {A}\)-disoptimal w.r.t. \(\texttt{int}\) on
is \(\mathcal {A}\)-disoptimal w.r.t. \(\texttt{int}\) on
 .
.
Proof
If
 is \(\mathcal {A}\)-disoptimal w.r.t.
is \(\mathcal {A}\)-disoptimal w.r.t.
 then
then
 , and therefore we have
, and therefore we have
 by definition of
by definition of
 , meaning that
, meaning that
 is an obsfuscator for what we observed in previous sections. On the other hand, if
is an obsfuscator for what we observed in previous sections. On the other hand, if
 , then surely we have
, then surely we have
 meaning that the specializer is
meaning that the specializer is
 -disoptimal.
-disoptimal.
At this point it should be clear why disoptimality is defined by keeping a (strict) approximation relation and not by losing any relation. Indeed, in this way it guarantees the semantics observed on the obfuscated program to be conservative w.r.t. the original semantics by containing it. In this way, while we force to lose the property we aim at obfuscating, we also partially keep the semantics of the original program by over approximating it.
Finally, since
 -disoptimality depends on both the specializer and the interpreter, we can choose to force disoptimality by leaving the specializer unchanged, and by acting only on the interpreter. We characterize a distortion of the interpreter able to make the specializer
-disoptimality depends on both the specializer and the interpreter, we can choose to force disoptimality by leaving the specializer unchanged, and by acting only on the interpreter. We characterize a distortion of the interpreter able to make the specializer
 -disoptimal. This idea is enforced by two aspects: (1) Due to the construction proposed, the distortion can be simply characterized as a parser inductively transforming the code in a semantically equivalent programFootnote 11; (2) Distortion can be driven by the notion of completeness, which is a semantic property strongly related to optimality as shown before.
-disoptimal. This idea is enforced by two aspects: (1) Due to the construction proposed, the distortion can be simply characterized as a parser inductively transforming the code in a semantically equivalent programFootnote 11; (2) Distortion can be driven by the notion of completeness, which is a semantic property strongly related to optimality as shown before.
5.2 Distorting Interpreters
In order to understand how to distort interpreters for inducing incompleteness we observe the following facts:
-
For each (not straightforward) abstraction there always exists a program/code whose abstract semantics is incomplete, hence we can always characterize syntactic elements making an abstract semantics incomplete [23];
-
We can think of transforming statements that will be executed in a semantic preserving way, yet including these elements;
-
Clearly, it is not decidable to determine which statements will be executed, therefore in order to introduce incomplete syntactic elements in our code that will be surely executed, in general, we need to transform all program statements;
-
A language parser transforming each statements by introducing incomplete elements for a fixed abstraction
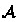 produces the required results.
produces the required results. -
By composing this parser with the interpreter, we obtain a distorted interpreter for which the control flow graph interpretation, i.e., its specialization w.r.t. the input program, is disoptimal, therefore obtaining an obfuscator obscuring the property expressed by
 on any input program.
on any input program.
We define a module that transforms the interpreter as a SFST accepting in input the language of the parser and in output the required syntactic transformation. This transducer is then composed with the interpreter, forcing the distorter output language to be the input one of the interpreter, hence generating a transformed CFG. This transformed CFG will be the source of interpretation.
Definition 10 (Interpreter Distorter)
Let
 be an interpreter accepting in input the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\). An interpreter distorter \(\texttt{D}\) is a SFST whose output language is a (strict) subset of \({{\,\mathrm{{\mathfrak {L}}}\,}}\) and preserving program semantics, i.e.,
be an interpreter accepting in input the language \({{\,\mathrm{{\mathfrak {L}}}\,}}\). An interpreter distorter \(\texttt{D}\) is a SFST whose output language is a (strict) subset of \({{\,\mathrm{{\mathfrak {L}}}\,}}\) and preserving program semantics, i.e.,
 is the distorted interpreter if
is the distorted interpreter if
 and
and
 .
.
Note that, if
 is the trivial transducer associated with \(\texttt{pars}\), then
is the trivial transducer associated with \(\texttt{pars}\), then
 .
.
Example: Trivial Syntactic Distorter. Suppose
 and
and
 be semantic preserving transformers, i.e.,
be semantic preserving transformers, i.e.,
 and
and
 , then the distorter in Fig. 6 is a trivial distorter, where the empty stack update
, then the distorter in Fig. 6 is a trivial distorter, where the empty stack update
 and the R moves are omitted in the transitions. As the parser, it is a symbolic pushdown automaton, which transforms the code while parsing it.
and the R moves are omitted in the transitions. As the parser, it is a symbolic pushdown automaton, which transforms the code while parsing it.
Theorem 3
Let
 be a
be a
 interpreter and let
interpreter and let
 be distorted by \(\texttt{D}\). Then
be distorted by \(\texttt{D}\). Then
 we have
we have
 .
.
This result tells us that the semantics of the program obtained by specializing the distorted interpreter is the same as the semantics of the original program, providing so far a potential obfuscation. Whether it is an obfuscation depends on the property we want to hide, and therefore it depends on the specific distortion and on the specific program semantics.
6 Obfuscation by Specializing Distorted Interpreters
In this section we show some examples of interpreter distortion making the CFG specializer disoptimal, therefore producing obfuscated code. As observed before, the first step is to fix the property to hide by obfuscation and a syntactic element making the analysis of this property incomplete. In other words, given a program property
 to hide, we define a
to hide, we define a
 -distorting interpreter, namely an interpreter for which the specializer implementing
-distorting interpreter, namely an interpreter for which the specializer implementing
 is
is
 -disoptimal. This is obtained by isolating a syntactic object producing imprecision and by embedding these objects into the code in such a way the abstract interpretation on
-disoptimal. This is obtained by isolating a syntactic object producing imprecision and by embedding these objects into the code in such a way the abstract interpretation on
 of the resulting program becomes incomplete.
of the resulting program becomes incomplete.
As an example, in order to obfuscate the program control flow we observe that incompleteness is obtained by injecting opaque predicates in the program [20], hence by using the trivial interpreter distorter we can obfuscate CFG simply by defining the following transformers where
 is an opaque predicate (e.g., an always true predicate),
is an opaque predicate (e.g., an always true predicate),
 and
and
 .Footnote 12
.Footnote 12

Data Obfuscation: Parity Obfuscation. Suppose we aim at obfuscating the parity \({ Par}\) (formalized as the well-known parity abstraction on numerical values) observation of data [18], i.e., of variable integer valuesFootnote 13. First of all we provide a general data abstraction distorter, where we define an expression transformers (
 and
and
 ) executing a value transformation hiding the property to obfuscate when storing data, and a complementary (i.e., which composed returns the identity) transformation when accessing data [18]. For instance, for obfuscating parity, when we store data we can multiply by \(2\) (hiding parity), and therefore when we access data we have to divide by \(2\). In order to make everything work, we have to make analogous transformations of variables values at the beginning (
) executing a value transformation hiding the property to obfuscate when storing data, and a complementary (i.e., which composed returns the identity) transformation when accessing data [18]. For instance, for obfuscating parity, when we store data we can multiply by \(2\) (hiding parity), and therefore when we access data we have to divide by \(2\). In order to make everything work, we have to make analogous transformations of variables values at the beginning (
 ) and at the end of the program (
) and at the end of the program (
 ). Hence, a simple pushdown automaton is not sufficient since, for these last variables updates, we have to scan the whole program for collecting variable names. In particular, in Fig. 7 we define
). Hence, a simple pushdown automaton is not sufficient since, for these last variables updates, we have to scan the whole program for collecting variable names. In particular, in Fig. 7 we define
 , where \(q_4\) extracts all the variables accessed in the program and put them on a stack (\({ var}(\textsf{e})\) and \({ var}(\textsf{b})\) are sequences of identifiers), \(q_5\) goes back to beginning of the program and \(q_6\) adds, at the beginning, an assignment involving each variable extracted to which we assign its transformation by
, where \(q_4\) extracts all the variables accessed in the program and put them on a stack (\({ var}(\textsf{e})\) and \({ var}(\textsf{b})\) are sequences of identifiers), \(q_5\) goes back to beginning of the program and \(q_6\) adds, at the beginning, an assignment involving each variable extracted to which we assign its transformation by
 . While creating this assignments we keep in the stack
. While creating this assignments we keep in the stack
 the names of all the variables for creating the final assignments at the end of the program (state \(q_7\)) assigning to each variable its transformation by
the names of all the variables for creating the final assignments at the end of the program (state \(q_7\)) assigning to each variable its transformation by
 .
.
Hence, we define
 by defining the transformations
by defining the transformations
 ,
,
 ,
,
 and
and
 as follows, where
as follows, where


In Fig. 8, on the left, we have the parity obfuscation of the program whose CFG is depicted in Fig. 2. The following theorem tells us that the so far designed interpreter distorter provides us with a parity obfuscation technique by specializing the distorted interpreter. Intuitively, at the first access to each variable, by dividing by 2 its value, we lose its parity, adding analysis imprecision and making so far the abstract parity interpreter incomplete, the specializer disoptimal and the resulting program obfuscated w.r.t. parity.
Theorem 4
Let
 be the distorted interpreter. It is a \({ Par}\)-distorting interpreter, meaning that
be the distorted interpreter. It is a \({ Par}\)-distorting interpreter, meaning that

 is an obfuscation of
is an obfuscation of
 w.r.t
w.r.t
 .
.
Control Obfuscation: CFG Flattening. The last example consists in obfuscating the CFG by flattening its structure [7, 36]. For obfuscating programs by flattening the CFG it is sufficient to make the program counter (\({ pc}\)) dynamic, i.e., a variable of the program manipulated during execution. Indeed, in this way the CFG observation (and therefore any CFG property) becomes imprecise [20]. Hence the idea is precisely to provide the transformers distorting the interpreter by handling the program counter while executing the program.
Then, let us consider the new variable \({ pc}\), we define the distorted parser by inserting each statement in a branch of a non-deterministic choice, whose guard is the value of \({ pc}\), value that is created and updated during execution. Also this distorter
 (Fig. 9) cannot be simply a pushdown automaton for two issues to face. First, we have to count the number of deterministic choices we insert, in order to know how many brackets
(Fig. 9) cannot be simply a pushdown automaton for two issues to face. First, we have to count the number of deterministic choices we insert, in order to know how many brackets
 we have to insert at the end (\(q_4\)). The stack cl is used precisely with this purpose. The other issue to face, is the fact that when we read
we have to insert at the end (\(q_4\)). The stack cl is used precisely with this purpose. The other issue to face, is the fact that when we read
 or
or
 we cannot know how many statement we will have respectively in the body or in the first branch, hence we cannot predict the value for \({ pc}\) that we can use for skipping the loop or for the other branch. For this reason we use two stacks p (principal) and s (secondary) in order to keep two disjoint chains of values for \({ pc}\) (even and odd values). Finally we have another stack c for keeping trace of the \({ pc}\) of the first statement of a loop and of the final \({ pc}\) of a branch. Moreover, we consider a special value
we cannot know how many statement we will have respectively in the body or in the first branch, hence we cannot predict the value for \({ pc}\) that we can use for skipping the loop or for the other branch. For this reason we use two stacks p (principal) and s (secondary) in order to keep two disjoint chains of values for \({ pc}\) (even and odd values). Finally we have another stack c for keeping trace of the \({ pc}\) of the first statement of a loop and of the final \({ pc}\) of a branch. Moreover, we consider a special value
 as final \({ pc}\).
as final \({ pc}\).
On the right of Fig. 8 the obfuscation of the program whose CFG is depicted in Fig. 2.
Formally, let us characterize the semantic abstraction made incomplete by flattening the program. Here we can simplify the previous characterization [20] since it is sufficient to find an abstraction made incomplete by a dynamic \({ pc}\) (we are not looking for an abstraction incomplete iff the \({ pc}\) is dynamic), and it should be clear that such an abstraction is precisely the CFG: Let us define

where it is well known that program collecting semantics is an abstraction of its small-step semantics and
In this way, it should be clear that
 is an abstraction of
is an abstraction of
 , since the set of possible executions contains the set of executionsFootnote 14.
, since the set of possible executions contains the set of executionsFootnote 14.
The following theorem tells us that in order to lose any property of the CFG structure we need to handle the program counter (\({ pc}\)) deciding the next statement to execute in the program. Intuitively in this way the semantic abstraction, by abstracting the guards involving the \({ pc}\), loses the CFG structure, and therefore any of its properties.
Theorem 5
Let
 be the distorted interpreter. It is a \({\mathcal {F}}\)-distorting interpreter, meaning that
be the distorted interpreter. It is a \({\mathcal {F}}\)-distorting interpreter, meaning that

 is an obfuscation of
is an obfuscation of
 w.r.t
w.r.t
 .
.
7 Conclusions
Our paper shows that code transformations for anti reverse engineering, such as code obfuscating transformations, can be designed systematically by specializing distorted interpreters. The idea proposed is to design an obfuscation starting from the static property \(\pi \) to conceal and determining syntactic elements such that the static analysis of \(\pi \) is imprecise/incomplete. Then we can build a distorter \(\texttt{D}\) inductively embedding these elements in single statements of programs without changing their semantics. Finally the distorted interpreter we obtain so far becomes an obfuscator of \(\pi \) when specialized w.r.t. the program to obfuscate, since for the resulting program the static analysis of \(\pi \) is forced to be incomplete. The result is a systematic method for building obfuscating compilers as straight applications of the well known Futamura’s projections, therefore going beyond the very first approach [20].
On the Limits of the Approach. The main limit of the proposed approach consists in the fact that it is built on a static model of attacker, namely aiming at defeating reverse engineering techniques based on static program analyses. In particular, on the one hand we believe that it is possible to capture any obfuscation technique where the information to obfuscate is a (static) program property that can be characterized as program/code abstraction, such as slicing obfuscation and opaque predicate obfuscation, on the other hand there probably exist dynamic obfuscation techniques that may not be modeled in the framework as it is, such as self-modifying code and virtualization. Indeed, what we propose is an interpreter distortion based on the distortion of the parser, which is a distortion limited to obfuscating properties strictly depending on how the code is written, namely for deceiving static analyses. Nevertheless, the separation of the static and the dynamic phases of the interpreter suggests us that we could try to capture other obfuscation techniques by distorting the semantic interpretation phase, where it is plausible to think of making possible to obfuscate dynamic analyses, but this clearly needs further work.
Another limit of this work is that it is not yet evaluated by means of an implementation. Anyway we believe that this will not represent a problem at least as far as the computational impact is concerned, since once we have built the interpreter depending on the property to obfuscate, then the complexity of the specialization is linear on the length of the program (transformation is performed while parsing the code). While, as far as the computational overhead of the obfuscated program is concerned, it does not depend on the proposed approach but on the way the code is transformed, and therefore on the specific chosen transformation.
Future Works. The notion of Jones optimality can be seen in a wider perspective, not just as a method for removing the overhead in time complexity, but as an universal paradigm to determine when a specializer applied to an interpreter and a program reestablish the initial conditions of the program relatively to some measure [6]. Hence, the existence of Jones optimal specializers is a key aspect in modern PL research (e.g., see the Brown and Palsberg striking result [3]). We believe that widening the range of applicability of the notion of Jones optimality to different (complexity) measures may provide the perfect theoretical framework to understand how the intensional nature of code affects the way we analyze it. Our paper provides a very first application to the case of the precision of an abstract interpreter.
Notes
- 1.
We avoid labels and initial and final brackets being not used in the semantics.
- 2.
Being the machine non deterministic with \(\epsilon \)-transition, w.l.g., we can suppose to have only one final state.
- 3.
Every FSM has a (only) readable input tape, where it is possible only to move right after each step, a finite state pushdown automaton is an automaton with also one stack, in any other cases we have a Turing Machine.
- 4.
Where R stands for move-right, L for move-left, and H for halt, and \(\{R,L,H\}^0\) means there is no writable input tape.
- 5.
We avoid the interpretation function [17] simply by denoting directly the predicates extensionally, as the sets of the elements satisfying the predicate.
- 6.
If \(\sigma =s_0\cdot s_1\cdots s_n\) then
 means that
means that
 , and
, and
 where \(\cdot \) stands for string concatenation.
where \(\cdot \) stands for string concatenation. - 7.
In this case the stack is not really symbolic.
- 8.
For the sake of readability we write s for singleton predicates \(\{s\}\) and the empty updates of the stack, i.e., \(\varepsilon \rightarrow \varepsilon \), are not depicted.
- 9.
Given an extensive and monotone function f, its least fix-point computation starting from x is
 , where \(f^0(x)=x\) and
, where \(f^0(x)=x\) and
 .
. - 10.
In this case, we consider directly the semantic abstraction induced by a memory abstraction \(\rho \) since we are abstracting in the semantic interpretation phase.
- 11.
Note that semantic equivalence on single (atomic) statements is decidable.
- 12.
For space reasons, and being quite intuitive, we do not provide the whole formalization of obfuscation by opaque predicates.
- 13.
For the sake of simplicity we suppose, without losing generality, that variables can only contain integer values, not boolean.
- 14.
We can also let the computations start from a subset of initial memories.
References
Arceri, V., Mastroeni, I.: Analyzing dynamic code: a sound abstract interpreter for evil eval. ACM Trans. Priv. Secur. 24(2), 10:1–10:38 (2021)
Barak, B., et al.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Brown, M., Palsberg, J.: Jones-optimal partial evaluation by specialization-safe normalization. Proc. ACM Program. Lang. 2(POPL), 14:1–14:28 (2018). https://doi.org/10.1145/3158102
Bruni, R., Giacobazzi, R., Gori, R., Garcia-Contreras, I., Pavlovic, D.: Abstract extensionality: on the properties of incomplete abstract interpretations. Proc. ACM Program. Lang. 4(POPL), 28:1–28:28 (2020). https://doi.org/10.1145/3371096
Bruni, R., Giacobazzi, R., Gori, R., Ranzato, F.: A logic for locally complete abstract interpretations. In: Symposium on Logic in Computer Science, LICS, pp. 1–13. IEEE (2021)
Campion, M., Dalla Preda, M., Giacobazzi, R.: Partial (in)completeness in abstract interpretation: limiting the imprecision in program analysis. Proc. ACM Program. Lang. 6(POPL), 1–31 (2022). https://doi.org/10.1145/3498721
Chow, S., Eisen, P., Johnson, H., van Oorschot, P.C.: A white-box DES implementation for DRM applications. In: Feigenbaum, J. (ed.) DRM 2002. LNCS, vol. 2696, pp. 1–15. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-44993-5_1
Collberg, C., Herzberg, A., Gu, Y., Giacobazzi, R., Wang, F., Davidson, J.: Toward digital asset protection. IEEE Intell. Syst. 26(06), 8–13 (2011). https://doi.org/10.1109/MIS.2011.106
Collberg, C., Nagra, J.: Surreptitious Software: Obfuscation, Watermarking, and Tamperproofing for Software Protection. Addison-Wesley Professional, Boston (2009)
Collberg, C., Thomborson, C.: Watermarking, tamper-proofing, and obduscation-tools for software protection. IEEE Trans. Software Eng. 735–746 (2002)
Consel, C., Lawall, J., Meur, A.F.L.: A tour of Tempo: a program specializer for the C language. Sci. Comput. Program. 52(17(1)), 47–92 (2004)
Cousot, P.: Constructive design of a hierarchy of semantics of a transition system by abstract interpretation. Theor. Comput. Sci. 277(1–2), 47–103 (2002)
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Conference Record of the 4th ACM Symposium on Principles of Programming Languages (POPL 1977), pp. 238–252. ACM Press (1977)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: Conference Record of the 6th ACM Symposium on Principles of Programming Languages ( POPL 1979), pp. 269–282. ACM Press (1979)
Cousot, P., Giacobazzi, R., Ranzato, F.: A\({^2}\)i: abstract\({^2}\) interpretation. Proc. ACM Program. Lang. 3(POPL), 42:1–42:31 (2019)
Dalla Preda, M., Mastroeni, I.: Characterizing a property-driven obfuscation strategy. J. Comput. Secur. 26(1), 31–69 (2018)
D’Antoni, L., Veanes, M.: Minimization of symbolic automata. In: POPL, pp. 541–554 (2014)
Drape, S.: Obfuscation of abstract data-types. Ph.D. thesis, University of Oxford (2004)
Giacobazzi, R.: Hiding information in completeness holes - new perspectives in code obfuscation and watermarking. In: Proceedings of the 6th IEEE International Conferences on Software Engineering and Formal Methods (SEFM 2008), pp. 7–20. IEEE Press (2008)
Giacobazzi, R., Jones, N.D., Mastroeni, I.: Obfuscation by partial evaluation of distorted interpreters. In: Kiselyov, O., Thompson, S. (eds.) Proceedings of the ACM SIGPLAN Symposium on Partial Evaluation and Semantics-Based Program Manipulation (PEPM 2012), pp. 63–72. ACM Press (2012)
Giacobazzi, R., Mastroeni, I., Dalla Preda, M.: Maximal incompleteness as obfuscation potency. Formal Asp. Comput. 29(1), 3–31 (2017)
Giacobazzi, R., Ranzato, F., Scozzari., F.: Making abstract interpretation complete. J. ACM 47(2), 361–416 (2000)
Giacobazzi, R., Logozzo, F., Ranzato, F.: Analyzing program analyses. In: Rajamani, S.K., Walker, D. (eds.) Proceedings of the 42nd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2015, Mumbai, India, 15–17 January 2015, pp. 261–273. ACM (2015)
Giacobazzi, R., Pavlovic, D., Terauchi, T.: Intensional and extensional aspects of computation: From computability and complexity to program analysis and security (NII Shonan Meeting 2018-1). In: NII Shonan Meeting Report 2018 (2018)
Glück, R.: Jones optimality, binding-time improvements, and the strength of program specializers. In: Asai, K., Chin, W. (eds.) Proceedings of the ACM SIGPLAN ASIA-PEPM 2002, Asian Symposium on Partial Evaluation and Semantics-Based Program Manipulation, Aizu, Japan, 12–14 September 2002, pp. 9–19. ACM (2002)
Jones, N.D.: Transformation by interpreter specialisation. Sci. Comput. Programm. 52(17(1)), 307–339 (2004)
Jones, N.D., Gomard, C.K., Sestoft, P.: Partial Evaluation and Automatic Program Generation. Prentice-Hall, Inc., Upper Saddle River (1993)
Jørgensen, J.: Similix: a self-applicable partial evaluator for scheme. In: Hatcliff, J., Mogensen, T.Æ., Thiemann, P. (eds.) DIKU 1998. LNCS, vol. 1706, pp. 83–107. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-47018-2_3
Leuschel, M.: Advanced logic program specialisation. In: Hatcliff, J., Mogensen, T.Æ., Thiemann, P. (eds.) DIKU 1998. LNCS, vol. 1706, pp. 271–292. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-47018-2_11
O’Hearn, P.W.: Incorrectness logic. Proc. ACM Program. Lang. (POPL) 4(10) (2020)
Rogers, H.: Theory of Recursive Functions and Effective Computability. The MIT Press, Cambridge (1992)
Romanenko, S.: Unmix, a Specializer for a Subset of Scheme. Keldysh Institute, Moscow (1993–2009). http://code.google.com/p/unmix/
Seidl, H., Wilhelm, R., Hack, S.: Compiler Design - Analysis and Transformation. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-17548-0
Thiemann, P.: Aspects of the PGG system: specialization for standard scheme. In: Hatcliff, J., Mogensen, T.Æ., Thiemann, P. (eds.) DIKU 1998. LNCS, vol. 1706, pp. 412–432. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-47018-2_17
Veanes, M., Hooimeijer, P., Livshits, B., Molnar, D., Bjørner, N.: Symbolic finite state transducers: algorithms and applications. In: POPL, pp. 137–150 (2012)
Wang, C., Davidson, J., Hill, J., Knight, J.: Protection of software-based survivability mechanisms. In: IEEE International Conference of Dependable Systems and Networks, Goteborg, pp. 193–202 (2001)
Winskel, G.: The Formal Semantics of Programming Languages: An Introduction. MIT Press, Cambridge (1993)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Giacobazzi, R., Mastroeni, I. (2022). Property-Driven Code Obfuscations Reinterpreting Jones-Optimality in Abstract Interpretation. In: Singh, G., Urban, C. (eds) Static Analysis. SAS 2022. Lecture Notes in Computer Science, vol 13790. Springer, Cham. https://doi.org/10.1007/978-3-031-22308-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-22308-2_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-22307-5
Online ISBN: 978-3-031-22308-2
eBook Packages: Computer ScienceComputer Science (R0)






 tape, a writable and readable input tape where we can stop or move left/right
tape, a writable and readable input tape where we can stop or move left/right (
( ,
,
 ,
,  , with
, with
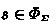 and
and
 .
. ;
;
 ;
; ;
; and
and  is graphically defined in Fig.
is graphically defined in Fig.  (
(
 ;
; and
and
 ;
; ;
; ;
; graphically defined in Fig.
graphically defined in Fig.  .
.


 -suboptimal w.r.t.
-suboptimal w.r.t.  (
(
 complete for
complete for  );
); (
(
 complete for
complete for 


 );
);
 (
(
 complete for
complete for

 complete for
complete for
 );
); (
(
 complete for
complete for


 ).
). . Suppose
. Suppose  , then it means that
, then it means that
 , therefore we have
, therefore we have
 hence we have completeness also for
hence we have completeness also for
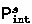 Analogously we can prove completeness for
Analogously we can prove completeness for
 when we have completeness for
when we have completeness for
 Intuitively, we have not the inverse implication since when
Intuitively, we have not the inverse implication since when  and
and
 we cannot imply anything on the optimality of the specializer, while when it is complete for both we can prove the following result.
we cannot imply anything on the optimality of the specializer, while when it is complete for both we can prove the following result. is complete for both
is complete for both
 and
and
 then
then
 and
and
 Therefore
Therefore
 meaning suboptimality w.r.t.
meaning suboptimality w.r.t.
 and
and

 Suppose
Suppose  , then it means that
, then it means that
 therefore we have
therefore we have
 Hence they are all equalities, and therefore we have completeness of
Hence they are all equalities, and therefore we have completeness of

 , we have
, we have  then
then
 hence we have
hence we have
 .
. produces the required results.
produces the required results. on any input program.
on any input program.

 .
.

 means that
means that
 , and
, and
 where
where  , where
, where  .
.