Keywords

1 Introduction

Nowadays, dual-arm robot manipulator robots are increasingly being applied in many different fields. Challenges in cooperative control include synchronizing position and controlling the force applied to an object. If too much force is applied to the object may deform its shape, or if the robot does not follow the predetermined path well, it can endanger the operator due to sudden movements. Therefore, it is necessary to design an efficient controller for this system to control position, orientation, and force with an uncertain dynamic model.

The problem of control under the kinematic uncertainty of the system has been solved by proposing the application of advanced control theories such as the sliding mode control in [1, 2] designed a controller for the robot to improve trajectory tracking quality. An adaptive controller for a dual-robot to hold an object with an unknown center of mass and moment of inertia has been proposed in [3]. A hybrid adaptive controller has been proposed in [4] to improve the efficiency of motion tracking and force adjustment when a cooperative dual-arm robot grasps an unknown object. In [5], a non-chattering robust sliding controller enhanced by a fuzzy logic unit to track the desired trajectory with high accuracy and safely transport the object. In addition, terminal sliding mode control (TSMC) is proposed by [6, 7] to improve the design of the sliding surface and lead to the tracking errors converging to zero in a finite time. In [8, 9] the authors present fast terminal sliding mode control (FTSMC) for nonlinear systems and demonstrate the convergent feature of the controller superior to the conventional sliding mode control.

An adaptive hybrid position/force controller using fuzzy backstepping has been proposed in [10], the fuzzy logic approximation properties are used to estimate the unknown dynamics of the system. The controller ensures that and the tracking errors of both position and force converge to the desired small value by selecting the appropriate design parameters. In [11] proposed an adaptive neuron force/position controller, the controller achieves the desired trajectories of the object and internal force tracking. A feedforward neural network is used to learn the unknown dynamics of the system with updated law based on Lyapunov stability analysis. Some research for the combined dual-arm robot system has solved two problems simultaneously: uncertain dynamic and uncertain environment. The neuron impedance controller has been proposed in [12] with two control loops, a position control loop and a force control loop to guarantee the desired trajectory and cooperation force. Several other powerful approximation techniques are based on differential equations or polynomials to estimate the uncertainty dynamic and disturbances of a multi-manipulators system moving an object [13, 14]. The robust adaptive controller proposed in [15] to deal with the problem of uncertain base coordinates, uncertainty model, and external disturbance, using the RBF neural network to estimate all kinds of these uncertainties.

Inspired by the analysis of previous studies mentioned above, in this paper, we focus on developing a generalized model for the dual-arm robot manipulator. Besides, an adaptive fast terminal sliding mode control is based on two neural networks to deal with nonlinear elements, uncertainties, and external disturbances. Finally, simulation results and conclusions are made to verify and show the achievements of this paper.

2 Dynamics of the Dual-Arm Robot–Object System

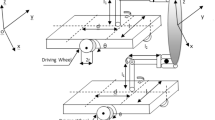
A dual-robot system under this study is illustrated in Fig. 1. The system consists of two manipulators arranged sort by duality, each arm is a robot with n degrees of freedom.

The coordinate frames are defined as follows:

  • {OXY}: The reference coordinate frame, located at the origin of the first robot arm;

  • {ovxvyv}: An object frame, located at the mass center of the object.

Ei \((i = 1 - 2)\) is the contact of the end-effector of the arm-robot ith with surface of the object; \(z = {[}r_{{o_{v} O}}^{T} ,\,\,\,\,\phi_{{o_{v} O}}^{T} {]}^{T}\) denotes the position \(r_{{o_{v} O}} = {[}x,\,y,\,z{]}^{T}\) vector and orientation \(\,\phi_{{o_{v} O}} = {[}\psi ,\,\,\varphi ,\,\theta {]}^{T}\) vector of the object frame concerning the reference coordinate frame; \(z_{{E_{i} o_{v} }} = {[}r_{{E_{i} o_{v} }}^{T} ,\,\,\,\phi_{{E_{i} o_{v} }}^{T} {]}^{T}\) denotes the position and orientation vector of the object frame concerning Ei frame.

Fig. 1.
figure 1

Model of a dual-arm robot holding an object

Full size image

The position and orientation of the object is determined through the homogenous transformation matrices of the corresponding coordinate frames and represented as follows:

$$ T_{O}^{{o_{v} }} = T_{O}^{{E_{i} }} .T_{{E_{i} }}^{{o_{v} }} . $$
(1)

From Eq. (1), the kinematic relationship between the object and the joint angles of the manipulators are built. From there, the relationship between the object’s motion velocity and the joint’s velocity is obtained [11]

$$ \dot{\user2{z}} = A_{i} \,\dot{\user2{q}}_{i} ;\,\,\user2{\ddot{z}} = A_{i} \,\user2{\ddot{q}} + \dot{A}_{i} \,\dot{\user2{q}} $$

That means

$$ \dot{\user2{q}} = A.\dot{\user2{z}};\,\,\user2{\ddot{q}} = A.\user2{\ddot{z}} + B\dot{\user2{z}}, $$
(2)

where \(A = {[(}A_{1}^{ - 1} )^{T} ,\,(A_{2}^{ - 1} {)}^{T} {]}^{T}\); \(\,B = {[( - }A_{1}^{ - 1} \dot{A}_{1} A_{1}^{ - 1} )^{T} ,\,\,( - A_{2}^{ - 1} \dot{A}_{2} A_{2}^{ - 1} {)}^{T} {]}^{T} .\)

The dynamic of the dual-arm can be formulated as in [10]

$$ H({\varvec{q}})\,\user2{\ddot{q}} + C({\varvec{q}},\dot{\user2{q}})\,\dot{\user2{q}} + G({\varvec{q}}) + {\varvec{\tau}}_{d} + J_{B}^{T} (q)\,F = {\varvec{\tau}}, $$
(3)

where \({\varvec{q}} = [{\varvec{q}}{\mkern 1mu}_{1}^{T} ,\,{\mkern 1mu} {\varvec{q}}_{2}^{T} ]^{T}\) is the joint angle \((2n \times 1)\) vector; \({\varvec{\tau}} = {[}{\varvec{\tau}}_{1}^{T} ,\,\,{\varvec{\tau}}_{2}^{T} {]}^{T}\) denotes the torque \((2n \times 1)\) vector applied to the joints; \({\varvec{\tau}}_{d} = {[}{\varvec{\tau}}_{d1}^{T} ,\,\,{\varvec{\tau}}_{d2}^{T} {]}^{T}\) denotes bounded unknown disturbances; \(F = {[}F_{1}^{T} ,\,\,F_{2}^{T} {]}^{T}\) is the vector of forces/moments on the object exerted by the manipulators at the end-effector; \(J_{B} ({\varvec{q}}) = {\text{blockdiag}}[J_{1} ({\varvec{q}}_{1} ),J_{2} ({\varvec{q}}_{2} ){]}\) represents the Jacobian analytical matrix of the manipulators; \(H({\varvec{q}}) = {\text{blockdiag[}}H_{1} ({\varvec{q}}_{1} ),\,\,H_{2} ({\varvec{q}}_{2} ){]}\), \(H_{i} (q_{i} )\) is the inertia matrix of the ith manipulator \(C({\varvec{q}},\dot{\user2{q}}) = {\text{blockdiag}}[C_{1} ({\varvec{q}}_{1} ,\dot{\user2{q}}_{1} ),\,\,C_{2} ({\varvec{q}}_{2} ,\dot{\user2{q}}_{2} ){]}\) denotes the matrix of Coriolis and centrifugal; \(G({\varvec{q}}) = {[}G_{1}^{T} ({\varvec{q}}_{1} ),\,\,G_{2}^{T} ({\varvec{q}}_{2} ){]}^{T}\) denotes the gravity vector.

The dynamic of the object also can be written in the following form [11]:

$$ H_{z} \,\user2{\ddot{z}} + C_{z} ({\varvec{z}},\dot{\user2{z}})\,\dot{\user2{z}} + g_{z} = F_{z} , $$
(4)

where \(H_{z} ,\,\,C_{z} ,\,\,g_{z}\) have the same meaning for the object as Eq. (3); \(F_{z}\) denotes the force/moment vector applied at the center of the object by the two manipulators.

Sum of force/moment applied at the object is expressed through the force and moment at the contact point generated by the manipulators at the end-effector: \(F_{z} = E\,F\), where E is the grasp matrix at the contact point, so:

$$ F = E^{ + } \,F_{z} , $$
(5)

where \(E^{ + } = E^{T} (E\,E^{T} )^{ - 1}\) is the pseudo-inverse of grasp-matrix E.

3 Fast Terminal Sliding Mode Controller Design

First of all, we define a reference velocity of the object by

$$ \dot{\user2{z}}_{r} = \dot{\user2{z}}_{d} + {{\varvec{\upgamma}}}{\varvec{e}}_{p} + {{\varvec{\upbeta}}}{\varvec{e}}_{p}^{\frac{m}{n}} , $$
(6)

where \({{\varvec{\upgamma}}} = diag\left( {\gamma_{1} ,\gamma_{2} ,\gamma_{3} ,\gamma_{4} ,\gamma_{5} ,\gamma_{6} } \right),\)\({{\varvec{\upbeta}}} = diag\left( {\beta_{1} ,\beta_{2} ,\beta_{3} ,\beta_{4} ,\beta_{5} ,\beta_{6} } \right),\)\(m,\,n\,\left( {m > n} \right)\) are positive odd numbers, and \(1 < \frac{m}{n} < 2\). The desired force is generated by an estimated reference model of the object as follows

$$ F_{z}^{d} = \hat{H}_{z} \user2{\ddot{z}}_{r} + \hat{C}_{z} ({\varvec{z}},\dot{\user2{z}}_{r} )\dot{\user2{z}}_{r} + \hat{g}_{z} $$
(7)

The reference model of the object is estimated by using RBFNN

$$ H_{z} \user2{\ddot{z}}_{r} + C_{z} ({\varvec{z}},\dot{\user2{z}}_{r} )\dot{\user2{z}}_{r} + g_{z} = {\text{W}}^{*T}_{0} \phi_{0} ({\varvec{x}}) + \varepsilon_{0} , $$
(8)

where \(\varepsilon_{0}\) is the approximate error, so

$$ \hat{H}_{z} \user2{\ddot{z}}_{r} + \hat{C}_{z} ({\varvec{z}},\dot{\user2{z}}_{r} )\dot{\user2{z}}_{r} + \hat{g}_{z} = {\hat{\text{W}}}^{T}_{0} \phi_{0} ({\varvec{x}}) $$

The tracking errors are defined \({\varvec{e}}_{p} = \left[ {\begin{array}{*{20}c} {e_{p1} } & {e_{p2} } & {e_{p3} } & {e_{p4} } & {e_{p5} } & {e_{p6} } \\ \end{array} } \right]^{T} = {\varvec{z}}_{d} - {\varvec{z}}\).

The error between actual and reference velocities is given by.

$$ {\varvec{s}}_{0} = \dot{\user2{z}} - \dot{\user2{z}}_{r} = - \dot{\user2{e}}_{p} - {{\varvec{\upgamma}}}{\varvec{e}}_{p} - {{\varvec{\upbeta}}}{\varvec{e}}_{p}^{\frac{m}{n}} $$
(9)

Consider that \({\varvec{s}}_{0} = 0,\) we have:

$$ \dot{\user2{e}}_{p} + {{\varvec{\upgamma}}}{\varvec{e}}_{p} + {{\varvec{\upbeta}}}{\varvec{e}}_{p}^{\frac{m}{n}} = 0\,{\text{or}}\,\dot{e}_{pk} + \gamma_{k} e_{pk} + \beta_{k} e_{pk}^{\frac{m}{n}} = 0 $$
(10)

in which \(k = 1 \div 6.\) Let \(u_{k} \user2{ = }e_{pk}^{\frac{1}{n}}\) then \(e_{pk}^{{}} \user2{ = }u_{k}^{n}\) substitute this into (10) leads to

$$ nu_{k}^{n - 1} \dot{u}_{k} = - \gamma_{k} u_{k}^{n} - \beta_{k} u_{k}^{m} $$
(11)

Divide both sides by \(u_{k}^{m}\) into (11) leads to

$$ nu_{k}^{n - m - 1} \frac{{du_{k} }}{{dt_{k} }} = - \gamma_{k} u_{k}^{\frac{n}{m}} - \beta_{k} $$
(12)

Integral of both sides into (12) leads to

$$ \int_{0}^{{t_{k} }} {dt_{k} = \int_{{{\mathbf{e}}_{pk} \left( 0 \right)}}^{0} {n\frac{{u_{k}^{n - m - 1} du_{k} }}{{ - \gamma_{k} u_{k}^{\frac{n}{m}} - \beta_{k} }}} } $$
(13)

Thus,

$$ t_{k} = \frac{n}{{\left( {n - m} \right)\gamma_{k} }}\left( {\ln \left( { - \gamma_{k} e_{pk}^{{1 - \frac{m}{n}}} \left( 0 \right) + \beta_{k} } \right) - \ln \beta_{k} } \right) $$
(14)

The desired force applied to the object is updated based on the estimates of the dynamic parameters of the object. The desired force at contact points should satisfy the relation given in (5)

$$ F^{d} = E^{ + } F_{z}^{d} $$
(15)

3.1 Design Control Law

Define the reference velocity of the ith robot: \(\dot{q}_{r}\).

The error between actual and reference velocities is given:

$$ {\varvec{s}} = \dot{\user2{q}} - \dot{\user2{q}}_{r} = A\,{\varvec{s}}_{0} $$
(16)

The dynamic of the dual-arm robot in Eq. (3), the matrices \(H(q),\,C(q)\), and vector \(G(q)\) contain all the parameters of the manipulators such as length, mass, and moment of inertia v.v. It is difficult to determine exact parameters due to errors in measurement, and environment v.v. Therefore, it is assumed that the components in Eq. (3) are written: \(H(q) = H_{0} (q) + \Delta H(q),\,C(q,\dot{q}) = C_{0} (q,\dot{q}) + \Delta C(q,\dot{q}),\,G(q) = G_{0} (q) + \Delta G(q)\), where \(H_{0} (q),\,C_{0} (q,\dot{q})\) and \(G_{0} (q)\) are nominal values and \(\Delta H(q),\,\Delta C(q,\dot{q})\) and \(\Delta G(q)\) are the component uncertainty of the dynamics model. So The dynamic of the dual-arm robot in Eq. (3) can be rewritten:

$$ H({\varvec{q}})\,\dot{s} = {\varvec{\tau}} - J_{B}^{T} ({\varvec{q}})\,F - f_{0} (q,\dot{q}_{r} ,\ddot{q}_{r} ) - C({\varvec{q}},\dot{\user2{q}})\,\,s - (\Delta f(q,\dot{q},\ddot{q}) + {\varvec{\tau}}_{d} ), $$
(17)

where \(f_{0} (q,\dot{q}_{r} ,\ddot{q}_{r} ) = H_{0} \ddot{q}_{r} + C_{0} \dot{q}_{r} + G_{0}\), \(\Delta f(q,\dot{q},\ddot{q}) = \Delta H\,\ddot{q} + \Delta C\,\dot{q} + \Delta G\)

The dynamic uncertainty and disturbances components are estimated using RBFNN.

$$ D = \Delta f(q,\dot{q},\ddot{q}) + {\varvec{\tau}}_{d} {\text{ = W}}^{*T} \phi (\overline{\user2{x}}) + {\varvec{\varepsilon}}, $$
(18)

where \(\varepsilon\) is the error approximation, so \(\hat{D}\) is the estimation of the function \(D\),

$$ \hat{D} = {\hat{\text{W}}}^{T} \phi (\overline{\user2{x}}) $$
(19)

So Eq. (17) as:

$$ H({\varvec{q}})\,\dot{\user2{s}} + C({\varvec{q}},\dot{\user2{q}})\,{\varvec{s}} + W^{*T} \phi (\overline{\user2{x}}) + {\varvec{\varepsilon}} = {\varvec{\tau}} - J_{B}^{T} ({\varvec{q}})\,F - f_{0} (q,\dot{q}_{r} ,\ddot{q}_{r} ) $$
(20)

Now, position control and force control without the measurement of force at contact points is proposed:

$$ {\varvec{\tau}} = f_{0} (q,\dot{q}_{r} ,\ddot{q}_{r} ) + {\hat{\text{W}}}\phi (\overline{\user2{x}}) + J_{B}^{T} F^{d} - K_{1} (A\,{\varvec{s}}_{0} ) - K_{2} {\text{sgn}} (s) - K_{3} {\text{sgn}} (s_{0} ) $$
(21)

3.2 Update Law for NN Weighs

Let an estimated error the dynamics of the object following is then obtained:

$$ \left( {H_{z} \user2{\ddot{z}} + C_{z} \dot{\user2{z}} + g_{z} } \right) - \left( {\hat{H}_{z} \user2{\ddot{z}}_{r} + \hat{C}_{z} \dot{\user2{z}}_{r} + \hat{g}_{z} } \right) = F_{z} - F_{z}^{d} $$
(22)

substitute Eqs. (8), (9) into (22) as:

$$ H_{z} \dot{\user2{s}}_{0} + C_{z} {\varvec{s}}_{0} + {\tilde{\text{W}}}_{0}^{T} \phi_{0} ({\varvec{x}}) + \varepsilon_{0} = F_{z} - F_{z}^{d} $$
(23)

The system is considered stable according to the Lyapunov stability principle, the candidate for the Lyapunov function can be selected as

$$ V = \frac{1}{2}{\varvec{s}}^{T} H\,{\varvec{s}} + \frac{1}{2}{\text{tr}}(\tilde{W}^{T} \,\varGamma^{ - 1} \tilde{W}) + \frac{1}{2}{\varvec{s}}_{0}^{T} H_{z} {\varvec{s}}_{0} + \frac{1}{2}{\text{tr}}(\tilde{W}_{0}^{T} \,\varGamma_{0}^{ - 1} \tilde{W}_{0} ) $$
(24)

The following lemmas as [11].

Lemma 1

\(A^{T} J_{B}^{T} = E\) and \(A^{T} J_{B}^{T} E^{ + } = I\), where I is the identity matrix.

The time derivative (24) of the Lyapunov function becomes:

$$ \dot{V} = {\varvec{s}}^{T} H\,\dot{\user2{s}} + \frac{1}{2}{\varvec{s}}^{T} \,\dot{H}\,{\varvec{s}} + {\text{tr}}(\tilde{W}^{T} \,\varGamma^{ - 1} \dot{\tilde{W}}) + {\varvec{s}}_{0}^{T} H_{z} \dot{\user2{s}}_{0} + \frac{1}{2}{\varvec{s}}_{0}^{T} \dot{H}_{z} {\varvec{s}}_{0} + {\text{tr}}(\tilde{W}_{0}^{T} \,\varGamma_{0}^{ - 1} \dot{\tilde{W}}_{0} ) $$

Using Eqs. (20) and (23) and the matric \(\dot{H} - 2C\) and \(\dot{H}_{z} - 2C_{z}\) are skew-symmetric, so \({\varvec{s}}^{T} (\dot{H} - 2C){\varvec{s}} = 0\) and \({\varvec{s}}_{0}^{T} (\dot{H}_{z} - 2C_{z} ){\varvec{s}}_{0} = 0\). Using Eqs. (15), (16) and due to properties of matrices \({\varvec{s}}_{0}^{T} A^{T} = (A\,\,{\varvec{s}}_{0} )^{T}\), and using Lemma 1, the derivative of the Lyapunov is determined as follows:

$$ \begin{aligned} & \dot{V} \le - (A\,\,{\varvec{s}}_{0} )^{T} K_{s} A\,{\varvec{s}}_{0} - \left\| {s^{T} } \right\|\left( {K_{2} {\text{sgn}} (A\,{\varvec{s}}_{0} ) - \left\| \varepsilon \right\|} \right) - (A\,\,{\varvec{s}}_{0} )^{T} \tilde{W}^{T} \phi (\overline{\user2{x}}) \\ & + {\text{tr}}(\tilde{W}^{T} \,\varGamma^{ - 1} \dot{\tilde{W}}) - \left\| {s_{0}^{T} } \right\|\left( {K_{3} {\text{sgn}} (s_{0} ) - \left\| {\varepsilon_{0} } \right\|} \right) - {\varvec{s}}_{0}^{T} A^{T} J_{B}^{T} E^{ + } (F_{z} - F_{z}^{d} ) \\ & + {\varvec{s}}_{0}^{T} (F_{z} - F_{z}^{d} ) - {\varvec{s}}_{0}^{T} \tilde{W}_{0}^{T} \phi_{0} ({\varvec{x}}) + {\text{tr}}(\tilde{W}_{0}^{T} \varGamma_{0}^{ - 1} \dot{\tilde{W}}_{0} ) \\ \end{aligned} $$
(25)

According to the Lyapunov stability principle, the condition for stability of closed dynamics is \(\dot{V} \le 0\) then

$$ {\text{tr}}(\tilde{W}^{T} \,\varGamma^{ - 1} \dot{\tilde{W}}) - (A\,\,{\varvec{s}}_{0} )^{T} \tilde{W}^{T} \phi (\overline{\user2{x}}) = 0 $$

and

$$ {\text{tr}}(\tilde{W}_{0}^{T} \varGamma_{0}^{ - 1} \dot{\tilde{W}}_{0} ) - {\varvec{s}}_{0}^{T} \tilde{W}_{0}^{T} \phi_{0} ({\varvec{x}}) = 0 $$

So, the updated law for the weights of the neural network may have the form:

$$ \begin{aligned} & \dot{\hat{W}} = - \varGamma \phi (\overline{\user2{x}})\,(A\,{\varvec{s}}_{0} )^{T} \\ & \dot{\hat{W}}_{0} = - \varGamma_{0} \phi_{0} ({\varvec{x}})\,\,{\varvec{s}}_{0}^{T} \\ \end{aligned} $$
(26)

Now, the derivative of the Lyapunov function is as follows:

$$ \dot{V} \le - (A\,\,{\varvec{s}}_{0} )^{T} K_{s} A\,{\varvec{s}}_{0} - \left\| {s^{T} } \right\|\left( {K_{2} {\text{sgn}} (A\,{\varvec{s}}_{0} ) - \left\| \varepsilon \right\|} \right) - \left\| {s_{0}^{T} } \right\|\left( {K_{3} {\text{sgn}} (s_{0} ) - \left\| {\varepsilon_{0} } \right\|} \right) $$
(27)

If \(K_{2}\) and \(K_{3}\) are selected, \(K_{2} > \left\| \varepsilon \right\|;\,\,K_{3} > \left\| {\varepsilon_{0} } \right\|\) then \(\dot{V} \le 0\).

It is possible to prove that the dynamic system is stable under the control input (21) combined with the updated law (26). According to the Lyapunov stability principle, the system is stable.

4 Simulation Results

In this section, numerical simulation tests are carried out to illustrate the effectiveness of the proposed method. The dual-arm robot is specified, with each arm being a 3-DOF manipulator that works in 2D space to preserve the computational time. The desired position and rotation angle of the object are set out with initial and terminal values as follows:

$$ \begin{aligned} & x_{0} = 0.54\,\left( {\text{m}} \right);y_{0} = 1.4\left( {\text{m}} \right);\theta_{0} = 0\,\left( {{\text{rad}}} \right) \\ & x_{f} = 1.2\,\left( {\text{m}} \right);y_{f} = 1.9\,\left( {\text{m}} \right);\theta_{f} = 0.349\left( {{\text{rad}}} \right) \\ \end{aligned} $$

To ensure smooth motion, the quintic polynomial curve is employed to construct reference trajectories from the initial pose to the terminal pose. Choosing the execution time \(T_{f} = 2.0592\,\left( s \right)\), the desired path is given by:

$$ \begin{aligned} & x_{d} = 0.54 + 0.756t^{3} - 0.5508t^{4} + 0.107t^{5} \\ & y_{d} = 1.4 + 0.5728t^{3} - 0.4173t^{4} + 0.0811t^{5} \\ & \theta_{d} = 0.3999t^{3} - 0.2913t^{4} + 0.0566t^{5} \\ \end{aligned} $$

The parameters for proposed controller are chosen as.

\(K_{s} = diag\left( {\left[ {100,100,100,100,100,100} \right]} \right);{{\varvec{\upgamma}}} = diag\left( {\left[ {300,600,600} \right]} \right);{{\varvec{\upbeta}}} = diag\left( {\left[ {100,100,150} \right]} \right)\) For the RBF system, the number of neurons in hidden layer is 1000, the center and width of Gaussian function are \(linspace\left( { - 2,2,1000} \right)\) and 30 respectively, the adaptive gains are \(\varGamma = 200;\,\,\varGamma_{0} = 200\). Since it is difficult to obtain accurate system parameters, we assume the uncertainty accounts for 30% of total dynamic model. Furthermore, the external noises acting on each arm are presented in Fig. 2. To clearly show the advantages of the proposed method, the comparisons in terms of tracking performance between the FTSMC controller and FTSMC integrated with the RBF neural network are implemented. From a qualitative perspective, Figs. 3 and 4 show the object’s trajectory on the x-axis and y-axis, respectively. The rotation angle of the object is presented in Fig. 5. The blue line, green line, and red dash line indicate the tracking error of the NN-FTSMC, original FTSMC, and the reference path respectively. Although the FTSMC method expresses robustness against disturbances, its performance is still adversely impacted, leading to large errors in tracking trajectories, especially on the x and y axis. On the other hand, with the support of the RBF approximation, the effects of disturbances are compensated and adapted in the control signal. Therefore, the system can ensure both robust and adaptive properties. The tracking errors of the NN-FTSMC are much lesser than the original FTSMC. It can be seen more specific in quantitative results using the root mean square error (RMSE) metrics on tracking errors in x, y-axis, and rotation angle as in Table 1. As compared to the original FTSMC controller, the tracking errors of NN-FTSMC are improved significantly, with 75.7% on the x-axis, 59.01% on the y-axis, and 68.62% in the rotation angle.

Fig. 2.
figure 2

External disturbances

Full size image
Fig. 3.
figure 3

The trajectory of the object in x-axis

Full size image
Fig. 4.
figure 4

The trajectory of the object in y-axis

Full size image
Fig. 5.
figure 5

The rotation angle of the object

Full size image
Table 1. RMSE comparison
Full size table
Fig. 6.
figure 6

Total forces and moments acting on the center of the object

Full size image

The total forces and moments acting on the center of the object are also illustrated in Fig. 6. It can be seen that the sum of the forces and moments applied to the object at the balance position is zero, which means the object is held stable at the balance position. The sign function is substituted by the saturation function to alleviate the chattering phenomenon; hence, the control inputs are applicable in real systems.

5 Conclusion

This paper proposed a robust adaptive controller based on a neural network to control a dual-arm robot manipulator manipulating a rigid object with uncertainties and external disturbances. Since in practice, it is difficult to accurately determine the parameters of the dynamic model of the system, so using two NN algorithms to estimate the model uncertainty of the dual-arm robot, the external disturbance, and the applied force. The stability of the closed-loop control system is proven stable according to the Lyapunov stability theory. The online adaptive learning law is suggested to ensure a stable system by using the Lyapunov principle. The simulation results on Matlab/Simulink have confirmed the stability, robust, fast response, the trajectory of the object convergence with the error to zero, and the guaranteeing object holding stable at the balanced position of the proposed controller.