Keywords

1 Introduction and Motivation

A supply chain is a network of actors (companies and organizations) directly or indirectly involved in fulfilling a customer request. When dealing with goods manufacturing, the supply chain not only includes manufacturers and suppliers, but also transporters, warehouses, retailers, and customers themselves [16]. From the view of the focal enterprise, the operational functions in the supply chain can be defined as procurement, production, and distribution. These three main activities are highly interconnected, and decisions at each stage do impact the other stages. Indeed, at the operational level, for example, decisions regarding the frequency of raw material arrival from the supplier determines the earliest time a production order can start at the manufacturing floor, while the completion times of production orders at the manufacturer defines the order availability for delivery by the transporter. The opposite is also valid: production planning is influenced by the planning of transportation of finished products.

However, because of the complexity of such integrated problem, decisions regarding production and transportation are most frequently made separately so that efficiencies at each stage can be reached [4]. On another hand, in order to supply these requests, companies are forced to increase inventory levels without taking into account that they impact the logistics costs of the product [11]. According to the literature (e.g., [12, 19], the logistics costs can constitute up to 30% of the product’s final cost. At the same time, transportation and inventory holding are the logistics activities that mainly absorb costs. Empirical studies have shown that each of them represents between 50% and 66% of the total logistics costs [2].

In the search of alternatives that allow obtaining a balance between customer satisfaction and logistics costs, several approaches have been studied in the literature to optimize the design of distribution routes. By doing so, it is possible to achieve a reduction in total operating costs of between 3% and 20% [17]. The problem of designing distribution routes is generally approached in the literature as the Vehicle Routing Problem, which is known to be NP-hard, since it generalizes the Travelling Salesman Problem (TSP) and the Bin Packing Problem (BPP) which are both well-known NP-hard problems [6]. This intractability means that optimal solutions are difficult to obtain in reasonable computational time. Hence, researchers and practitioners alike prefer the use of approximate algorithms to solve these problems.

A huge variety of versions of the VRP has been studied in the literature, as witnessed by several recent literature review papers (i.e., [1, 3, 5, 7,8,9, 13,14,15]). Among the different variants, the vehicle routing problem with order ready times has been rarely studied. In such a context, the aim of this paper is to propose both a mathematical formulation and a solution procedure for the VRP with order release times (VRP-RT). This variant of the problem is inspired from industrial applications arising in the combined production scheduling and vehicle routing problem [10, 20].

This paper is organized as follows. Section 2 describes the problem under study and its mathematical formulation. The proposed solution procedure based on the hybridization of Iterated Local Search and Variable Neighborhood Descent (ILS-VND) is presented in Sect. 3. Computational experiments and the analysis of results are presented in Sect. 4. This paper ends in Sect. 5 by presenting some conclusions and drawing opportunities for future research.

2 Problem Description and Mathematical Model

Starting from a set of production orders manufactured at the production stage of a supply chain, they are then delivered to a set of geographically dispersed customers. The completion times of each production order once manufacturing has finished become a release or ready time for delivery start. This delivery of finished products is modeled as a vehicle routing problem with release times (VRP-RT), which is computationally difficult to solve since it belongs to the class of NP-hard problems.

Formally speaking, a set of n production orders are to be manufactured and then shipped to customers once completed. The delivery is carry out using an infinite fleet of vehicles (e.g., trucks) with unlimited capacity Vehicles leave the factory every h hours. Each production order \(B_{i}\) consists of a set j of products \(B_{i}=\{J_{i,1}...J_{i,n}\}\) to be delivered to a customer with a known location. In addition, each delivery order \(B_i\) has a release time \(C_i\) defined by the completion time of manufacturing. We consider that vehicles must return to the factory after the delivery route is completed. Therefore, the vehicle routing problem is modeled as a VRP with order release times. In addition, each route r includes a start travel time \(H_r\), a total travel time \(D_r\), and the delivery time of the last order \(CR_r\). The longest delivery time \(CR_{Max}\) is defined as \(\max \{ CRr\} \forall r \in R\). The routing problem is modeled in a complete undirected graph \(G'=(V',A')\), where \(V'=(1...n)\) is the set of nodes (clients), and \(A'\) is the set of arcs connecting each pair of nodes (clients). Each arc has a non-negative integer value \(T_{l,h}\) representing the time a vehicle travels from node l to node h.

Since the objective of the problem is to minimize the maximum delivery date of the orders \(CR_{Max}\), a mathematical program can be proposed as follows:

Sets:

  • I :  Order sets (\(i \in I=\{0,1....n\})\)

  • R Set of routes (\(r\in R=\{1....R_n\}\))

  • Alias: \(j=i\)

Parameters:

  • \(C_i:\) Release time of the order i.

  • \(T_{i,j}:\) Distance between points i, j.

  • M :  Very large number.

  • N :  Total number of orders.

  • R :  Total number of routes.

  • Mk :  Makespan.

  • \(C_{min}:\) Completion time of first order in production.

Decision variables:

  • \(H_r\): Route start time r.

  • \(D_r\): Route total travel time r.

  • \(BN_{i,r}=\) 1 if order i is shipped on route r, 0 otherwise

  • \(CR_{MAX}\): Delivery time of last order.

  • \(XR_{r,i,j}\) = 1 if order j is delivered after order i on route r, 0 otherwise

  • \(U_{r,i}\): Number of arcs of node j on route r

Objective function:

$$\begin{aligned} Min: CR_{MAX} \end{aligned}$$
(1)

S.A

$$\begin{aligned} H_r=C_{min}+ h \ \forall r=1 \end{aligned}$$
(2)
$$\begin{aligned} H_r= H_{r-1}+h\ \forall r>1 \end{aligned}$$
(3)
$$\begin{aligned} H_r+M*(1-BN_{i,r})\ge C_i \ \forall i \ \forall r \end{aligned}$$
(4)
$$\begin{aligned} \sum _{\forall r}{BN_{i,r}}=1 \forall i \end{aligned}$$
(5)
$$\begin{aligned} \sum _{\forall j\ne i \ne 0}{XR_{r,i,j}}=BN_{i,r} \forall i>0 \ \forall r \end{aligned}$$
(6)
$$\begin{aligned} \sum _{\forall i\ne j \ne 0}{XR_{r,i,j}=BN_{j,r}} \forall j>0 \ \ \forall r \end{aligned}$$
(7)
$$\begin{aligned} \sum _{\forall j}{XR_{r,0,j}}=1 \ \forall r \end{aligned}$$
(8)
$$\begin{aligned} \sum _{\forall i}{XR_{r,i,0}}=1 \ \forall r \end{aligned}$$
(9)
$$\begin{aligned} U_{r,i}+1\le N*(1-XR_{r,i,j})+U_{r,j}) \ \ \forall i>0,j>0 \ \forall j\ne i \ \forall r \end{aligned}$$
(10)
$$\begin{aligned} D_r=\sum _{\forall i}{\sum _{\forall j}{ T_{i,j}*XR_{r,i,j}}} \ \forall r \end{aligned}$$
(11)
$$\begin{aligned} CR_{MAX} \ge D_r+H_r \ \forall r \end{aligned}$$
(12)
$$\begin{aligned} H_r,D_r\in Z \ \forall r \end{aligned}$$
(13)
$$\begin{aligned} BN_{i,r}\in \{0,1\} \ \ \forall r\ \forall i \end{aligned}$$
(14)
$$\begin{aligned} XR{r,i,j}\in \{0,1\} \ \ \forall r\ \forall i \ \forall j \end{aligned}$$
(15)
$$\begin{aligned} CR_{MAX} \in Z \end{aligned}$$
(16)

In this mathematical formulation, constraints (2) ensure that the first vehicle undertakes the trip h time units after the production system finishes processing the first order. Constraints (3) declare that subsequent trips start at intervals of h time units. Constraints (4) guarantee that orders start after the production completion time. Constraints (5), (6) and (7) make sure that all orders are assigned to a vehicle. Constraints (8) and (9) guarantee that the vehicle on each route starts and ends the route at the factory. Equations (10) correspond to subtour elimination. The total travel time for each r is calculated using Constraints (11). Constraints (12) compute the longest delivery time in the system. Finally, Constraints (13), (14), (15) and (16) ensure values of decision variables.

3 Proposed Solution Procedure

This paper proposes the solution approach shown in Fig. 1. This solution approach is divided into five steps. In the first step, the start times of each vehicle are determined and the orders to be delivered are assigned to the vehicle. For the allocation, the vehicle loads all orders that have a release time lower than the route start time and that have not been allocated yet. Next, the Nearest Neighbor (NN) heuristic is used to obtain an initial solution for each route. To improve these solutions, the Iterative Local Search (ILS) metaheuristic hybridized with the Variable Neighborhood Descent (VND) heuristic. Finally, the maximum delivery time is calculated.

Fig. 1.
figure 1

Solution approach

Full size image
figure a

The ILS metaheuristic is described in Algorithm 1, where \(S_0\) is the initial solution obtained with the NN heuristic. The current solution is defined as S while the best solution is defined as BS. In line 1, the algorithm improves the initial solution using the VND heuristic. In line 2, the best solution of the problem is updated. The loop between line 4 and line 8 is executed until the running time of the algorithm has elapsed. In line 4, a perturbation is applied to the current solution in order to avoid staying in a local optimum solution. This paper uses the 2-OPT movement. Line 5 refreshes the current solution using the VND heuristic. Line 6 evaluates if the current solution is the best available solution. If so, the best solution of the algorithm is updated in line 7.

The VND algorithm is described in Algorithm 2, where \(S_0\) is defined as the initial solution, S as the current solution and \(S*\) as the local solution of the algorithm. N is the set of neighborhoods, while K is the index of N and T as the total number of neighborhoods. N is composed of the “Relocate” and “Swap” moves and are explained next. The algorithm starts by converting the initial solution into the current solution and into the best solution (see lines 1 and 2). In line 3, the first neighborhood of N is selected. Until the local search has been applied to the last neighborhood, the algorithm is executed cyclically from line 5 to line 11. In line 5, S is updated by applying the local search on the \(N_k\) neighborhood. In local search algorithm, best move that improves the assignment is selected. An evaluation is made to see if the current solution is better than the local solution in line 6. If so, the local solution is updated and the search is directed to neighborhood 1 (see lines 7 and 8). Otherwise, the algorithm moves to the next neighborhood (see line 10). Finally in line 12, the best local solution is returned.

figure b

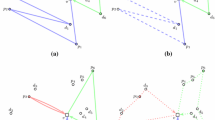
Neighborhoods. The neighborhoods used to solve this problem were Relocate and Swap. Relocate is performed between the same route and on other routes. In order to apply Relocate on other routes, we evaluate if the vehicle start time is greater than the order release time. When this occurs, \(\Delta _A\) and \(\Delta _B\) are determined as shown in Eqs.  (17) and (18). In Fig. 2, node x, which belongs to route B and is located between nodes i and j (see graph 1), is relocated on route A between nodes k and l (see graph 2). To compute the new \(CR_{Max}\), Eq. (19) is used. If the movement is applied on the same route to update the \(CR_{max}\), we use Eq. (20).

$$\begin{aligned} \Delta _A=T_{i,j}-T_{i,x}-T_{x,j} \end{aligned}$$
(17)
$$\begin{aligned} \Delta _B=T_{k,x}+T_{x,l}-T_{k,l} \end{aligned}$$
(18)
$$\begin{aligned} CR_{MAX}=\max \{CR_A+\Delta _A,CR_B+\Delta _B,\max \{CR_r\} \forall r\in R- \{A,B\}\} \end{aligned}$$
(19)
$$\begin{aligned} CR_{A}=CR_A+\Delta _A+\Delta _B \end{aligned}$$
(20)
Fig. 2.
figure 2

Relocate

Full size image

4 Computational Experiments and Results

The proposed solution approach was run on a PC with 4.1 GHz, 4 cores and 20 GB RAM. Since there are not benchmark instances available in the literature for the problem under study, experiments were carried out by adapting the VRP datasets from [18]. The mathematical model was coded in Python programming language and solved using Gurobi 9.12 and the solver CPLEX 20.10, while the algorithm was coded in Java language. To divide the routes, we established that each vehicle starts its delivery every 2 h from the factory.

4.1 Algorithm Calibration

In order to calibrate the parameters of the algorithm, a preliminary experiment was carried out using a sample of five (out of 30) instances. These instances were selected based on their size. The instances selected allowed to define the running time of the algorithm. Each of these instances was run for one hour and convergence curves were drawn (see Fig. 3). Most of the instances converge in less than one minute. However, instance TRM30 converges in around 2 min. Therefore, the running time for the other instances was set to 5 min to prevent losing good results.

Fig. 3.
figure 3

Algorithm convergence

Full size image
Fig. 4.
figure 4

Box-plot factorial experiment

Full size image

A factorial experiment was also designed to define the order of execution of the two neighborhoods in the VND algorithm. This experiment is composed of two factors. The first factor evaluates which of the two neighborhoods should be executed first, while the second factor is the set of five instances previously selected. Each experiment was run for 5 min as defined above, and run using three replications to obtain statistical results. The best solution and the time required to reach it are both registered. Figure 4 contains the box plot for the \(CR_{MAX}\) and running time. In addition, we verified that output variable \(CR_{MAX}\) meets the assumptions of normality, stochasticity and independence. For this, we used Kolmogorov-Smirnov, Bartlett and Durbin-Watson tests. The sample gave us that the residuals do not behave normally, therefore a parametric test cannot be applied. Therefore, nonparametric Wilcoxon signed-rank test for related data was selected with 95% confidence level. It was obtained that the order of execution of the neighborhoods does not significantly influence \(CR_{MAX}\), as illustrated in Fig. 4. Also, to identify if there is a significant difference around the running time of the algorithm, normality assumptions were tested. As a result, the sample errors with respect to time do not behave normally. Considering that the data are not related, the Wilcox test was hence performed, giving as a result that there is a significant difference in the time to obtain the best solutions. To sum up, this experiment showed that there is no significant difference in the order of execution of the neighborhoods, but results are obtained faster if the swap neighborhood is executed before relocate. Therefore, this neighborhood configuration was used for the full computational experiment.

Table 1. Computations results
Full size table
Table 2. ILS and CPLEX comparison
Full size table

4.2 Computational Results

The computational results for the set of 30 instances are presented in Table 1. For each instance, five replications were performed. In Table 1 the number of clients of the instance is shown. The best solution of the algorithm, the average of the five replications, the worst solution found and the standard deviation for each instance are reported. Also, the table reports the lowest, the average and the highest response time for each instance. The first conclusion from these results is that the proposed algorithm has a low variance. In addition, a comparison with the solution obtained with the mathematical model is presented (see Table 2). The execution time of the mathematical model was limited to three hours per instance. From the results returned by the solver, the table reports the relaxed lower bound, the integer feasible solution (if found), the GAP between them, and the running time. From these results, four optimal solutions were found (TRM18, TRM19, TRM23 and TRM24), while the solver could not find feasible solutions for instances TRM11, TRM14, TRM21, TRM22 and TRM30. For the solutions that are feasible, the most complex instances are TRM0, TRM1, TRM2, TRM3, TRM4, TRM5, TRM6, TRM7, TRM8 and TRM9.

Comparing the feasible results returned by the ILS-VND algorithm with the solver, it is observed that the algorithm in a short period of time yields to better solutions. In addition, we observe that the algorithm is able to find optimal solutions as it finds the optimum of the solutions TRM18, TRM19, TRM23 and TRM24. Moreover, for serveral instances (TRM0, TRM12, TRM16, TRM20, TRM21, TRM22, TRM25, TRM26 and TRM27) the gap is even lower than 3%, which is very good performance. Although for the most complex instances outlined above, the gap with respect to the relaxed lower bound is very high, and in most cases it outperforms the solutions found by the solver.

5 Conclusions and Perspectives

This paper proposed a mathematical model and a hybrid algorithm to solve the vehicle routing problem with order release times. This problem, inspired by practical real-life situations of production-distribution systems, has been rarely studied in the literature, making this paper one of the first contributions. The proposed algorithm consists on an Iterated Local Search and a Variable Neighborhood Descent. Computational experiments were carried out using adapted benchmark instances from the literature. Experimental results are promising and motivate further studies about this problem.

Following the findings of this work, several opportunities for further research are identified. For example, several parameter sets of the metaheuristic can be tested, followed by the design of a solution procedure that addresses the joint production and routing problem. It would also be interesting to formulate a multi-objective algorithm, to address also environmental or social performance indicators, in addition to routing costs or times. In addition, other constraints could be added to the problem, such as time windows, service times, vehicle capacity, etc.