Mind the Gap! Predictive Flocking of Aerial Robot Swarm in Cluttered Environments

Abstract

Flocking, coordinated movement of individuals, widely observed in animal societies, and it is commonly used to guide robot swarms in cluttered environments. In standard flocking models, robot swarms often use local interactions between the robots and obstacles to achieve safe collective motion using virtual forces. However, these models generally involve parameters that must be tuned specifically to the environmental layout to avoid collisions. In this paper, we propose a predictive flocking model that can perform safe collective motion in different environmental layouts without any need for parameter tuning. In the model, each robot constructs a search tree consisting of its predicted future states and utilizes a heuristic search to find the most promising future state to use as the next control input. Flocking performance of the model is compared against the standard flocking model in simulation in different environmental layouts, and it is validated indoors with a swarm of six quadcopters. The results show that more synchronized and robust flocking behavior can be achieved when robots use the predicted states rather than the current states of others.

1 Introduction

Flocking, the coherent motion of a group of individuals, is commonly encountered in animal societies [1] with schools of fish and flocks of birds demonstrating impressive examples of coordinated motion [10, 11]. Flocking has also been an interest in artificial systems. One of the earliest attempts to implement flocking in artificial systems is due to Reynolds [13]. In his model, flocking is modeled using repulsion, velocity alignment, and attraction behaviors. Repulsion ensures collision avoidance, velocity alignment maintains the coherent motion, and attraction keeps the flock together. Numerous flocking models have been proposed based on these interactions to describe various systems such as animal groups [5] and migrating cells [9].

In the virtual force model [16], these behaviors are generated via virtual forces exerted on the agents where the magnitude and direction of the forces depend on the local interactions between neighboring agents. The virtual force model is often used for implementing robot swarms in cluttered or confined environments due to its reactivity, and low computational complexity [7, 18]. However, these implementations frequently involve parameters that must be tuned specifically to the environmental layout. Consequently, sudden changes in the environmental layout may cause collisions or decrease flocking performance, which makes these models unreliable in real-world.

Recent studies [2, 6] claim that natural swarms, such as schools of fish or swarms of bats, use predicted future states of their neighbors rather than the current states. In accordance with this claim, in [3] it was demonstrated that the neural activity in bat’s brain encodes non-local navigational information up to a few meters away from the bat’s present state during both random exploration and goal-directed motion.

Inspired by the natural swarms, predictive flocking models based on distributed model predictive control (DMPC) have emerged since DMPC can handle actuation constraints of robots and optimize flocking performance [8, 14]. Previous work showed that aerial robot swarms using DMPC-based flocking model could perform safe collective motion with noisy sensor measurements in a cluttered environment [14] and in the presence of dynamic obstacles [8]. Although DMPC-based flocking models perform more robust collective motion compared to standard flocking models, their onboard implementation remains a challenge due to the computational complexity and the requirement of excessive communication between robots.

In this paper, we propose a novel flocking model based on a predictive search method that can perform safe collective motion in different environmental layouts without parameter tuning. In the proposed model, robots can sense obstacles and other robots within a limited range and only use the local information. Each robot constructs a search tree consisting of their possible future states and finds the trajectory that fulfills the flocking objectives by using a heuristic search algorithm to determine its next move.

2 Methodology

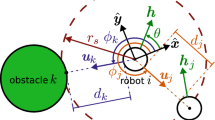
Consider a swarm consisting of N robots with a radius $r_a$ moving in a 2D environment. Robots can sense obstacles and other robots within a limited range, $r_s$. At each time step, $\varDelta t$, the next velocity of the robot is determined according to the updated information of the neighboring robots and obstacles. The number of neighbors and obstacles closest to robot i are indicated by M and O, respectively. Their values are limited to $M\le M_{max}$ and $O \le O_{max}$. The position and velocity of robot i are denoted by $\boldsymbol{p}_i$ and $\boldsymbol{v}_i$. The position of the point closest to robot i on the boundary of obstacle k is indicated by $\boldsymbol{o}_k$. The distance between robot i and its $j^{th}$ neighbor is denoted by $d_{ij}=\Vert \boldsymbol{p}_i - \boldsymbol{p}_j \Vert - 2r_a$ whereas the distance between robot i and obstacle k is indicated by $d_{ik}=\Vert \boldsymbol{p}_i - \boldsymbol{o}_k \Vert -r_a$. $\boldsymbol{v}_{mig}$ is defined as the migration velocity to the robots. Each robot moves in the direction of its heading $\boldsymbol{u}_i$, with the heading angle $\theta _i$ calculated with respect to the frame of reference (Fig. 1). Unit vectors along the x, y, and z-axis of the frame of reference are denoted by $\boldsymbol{\hat{x}}$, $\boldsymbol{\hat{y}}$ and $\boldsymbol{\hat{z}}$. The common frame of reference is used for ease of description. In the following models, a robot can calculate its next velocity using a local frame of reference and relative positions and velocities of others.

Fig. 1.

Illustration of a robot swarm in a 2D environment with (a) robot’s radius, heading angle, position and velocity vectors, (b) sensing range, heading, relative distances, and virtual forces.

2.1 Standard Flocking Model (SFM)

We extended the Active Elastic Sheet (AES) model [4], which uses spring-like virtual interaction forces between robots, by adding an obstacle avoidance force to prevent robot-obstacle collision and a migration force to provide migration velocity. The total force acting on robot i is obtained as the sum of three forces as:

$$\begin{aligned} \displaystyle \boldsymbol{f}_{i} = \boldsymbol{f}_{i}^{r} + \boldsymbol{f}_{i}^{o} + \boldsymbol{f}^{m} \end{aligned}$$

(1)

where $\boldsymbol{f}_{i}^{r}$ is the inter-robot force, $\boldsymbol{f}_{i}^{o}$ is the obstacle avoidance force and $\boldsymbol{f}^{m}$ is the migration force (Fig. 1b).

The spring-like inter-robot force is calculated as:

$$\begin{aligned} \displaystyle \boldsymbol{f}_{i}^{r} = \sum _{j=1}^{M} k^{r} \left( d_{ij} - d_{eq} \right) \boldsymbol{u}_{ij} \end{aligned}$$

(2)

where $k^{r}$ is the inter-robot force gain, $d_{eq}$ is the equilibrium distance and $\boldsymbol{u}_{ij}$ is the unit vector directed from robot i to its $j^{th}$ neighbor.

The obstacle avoidance force is calculated as:

$$\begin{aligned} \displaystyle \boldsymbol{f}_{i}^{o}= \sum _{k=1}^{O} -k^{o} \frac{1}{ d_{ik} ^2} \boldsymbol{u}_{ik} \end{aligned}$$

(3)

where $k^{o}$ is the obstacle avoidance force gain and $\boldsymbol{u}_{ik}$ is the unit vector directed from robot i to obstacle k. In [7], it has been shown that as the robot approaches an obstacle, the obstacle avoidance force must increase significantly compared to the inter-robot force to avoid the robot-obstacle collision. Thus, $\boldsymbol{f}^o_i$ designated as its magnitude increases exponentially as robot i gets closer to obstacle k, whereas the magnitude of $\boldsymbol{f}^r_i$ increases linearly as two robots get closer to each other.

The migration force keeps the velocity of robots at the migration velocity and it is calculated as:

$$\begin{aligned} \displaystyle \boldsymbol{f}^{m} = k^{m} \boldsymbol{v}_{mig} \end{aligned}$$

(4)

where $k^{m}$ is the migration force gain.

The linear speed of the robot is computed by projecting $\boldsymbol{f}_{i}$ onto $\boldsymbol{u}_i$ and multiplying it by the linear speed gain $k^{l}$ as:

$$\begin{aligned} \displaystyle v_{i} = k^{l} ( \boldsymbol{f}_{i} \cdot \boldsymbol{u}_i ). \end{aligned}$$

(5)

The angular speed of the robot is obtained by projecting $\boldsymbol{f}_{i}$ onto the vector perpendicular to its heading and multiplying it by the angular speed gain $k^{a}$ as:

$$\begin{aligned} \displaystyle \omega _{i} = k^{a} ( \boldsymbol{f}_{i} \cdot \boldsymbol{u}^{\perp }_i ). \end{aligned}$$

(6)

The linear speed is bounded between $v_{min}$ and $v_{max}$ whereas the angular speed is bounded between $-\omega _{max}$ and $\omega _{max}$. Then, the linear and angular velocities of robot i are obtained as:

$$\begin{aligned} \displaystyle \boldsymbol{v}_{i} = v_i \boldsymbol{u}_i, \end{aligned}$$

(7)

$$\begin{aligned} \displaystyle \boldsymbol{\omega }_{i} = \omega _i \boldsymbol{\hat{z}}. \end{aligned}$$

(8)

2.2 Predictive Flocking Model (PFM)

The predictive flocking model searches for a trajectory that fulfills the flocking objectives only using local information. Each robot constructs a search tree consisting of nodes that contain its possible future position and velocity states where levels of the search tree represent future time steps.

Let the heading angle and speed of a parent node at the $c^{th}$ level of the search tree be denoted by $\theta ^c$ and $v^c$, respectively. Then, the heading angle and speed values of its child nodes at the next level of the search tree are calculated as:

$$\begin{aligned} \displaystyle \theta ^{c+1}_{a} = \theta ^c + a \varDelta \theta \qquad a \in \mathbb {Z} : -A \le a \le A, \end{aligned}$$

(9)

$$\begin{aligned} \displaystyle {v}^{c+1}_{b} = v^c + b \varDelta v \qquad b \in \mathbb {Z} : -B \le b \le B \end{aligned}$$

(10)

where $\varDelta \theta$ and $\varDelta v$ are the search step parameters, A and B are the parameters that determine the number of considered reachable heading angle and speed values at the next time step, respectively. Since the calculated heading angle and speed values should satisfy the actuation constraints of the robot, the speed term ${v}^{c+1}_{b}$ is bounded between $v_{min}$ and $v_{max}$, and the parameters are selected as the constraints $A \varDelta \theta \le \omega _{max} \varDelta t$ and $B \varDelta v \le a_{max} \varDelta t$ are satisfied where $\omega _{max}$ and $a_{max}$ are the maximum angular speed and the maximum acceleration of the robot. Then, the velocity and position states of the child nodes are calculated as:

$$\begin{aligned} \displaystyle \boldsymbol{v}^{c+1}_{a,b} = {v}^{c+1}_{b} \big ( cos(\theta ^{c+1}_{a}) \boldsymbol{\hat{x}} + sin(\theta ^{c+1}_{a} ) \boldsymbol{\hat{y}} \big ), \end{aligned}$$

(11)

$$\begin{aligned} \displaystyle \boldsymbol{p}^{c+1}_{a,b} = \boldsymbol{p^c} + \varDelta t \boldsymbol{v}^{c+1}_{a,b} \end{aligned}$$

(12)

where $\boldsymbol{p}^c$ is the position state of the parent node.

Fig. 2.

Illustration of an example search tree for the parameters $\beta =2$, $d=2$, $A=1$ and $B=0$. $\boldsymbol{p}^0$ and $\boldsymbol{v}^0$ represent the current position and velocity of the robot. The gray nodes are pruned, and the remaining nodes are expanded. The next velocity of the robot is obtained as $\boldsymbol{v}^1_{-1,0}$ which is the first velocity state of the found trajectory.

The positions of the neighboring robots at the $c^{th}$ level of the search tree are predicted assuming their velocities remain the same as:

$$\begin{aligned} \displaystyle \boldsymbol{p}^c_j = \boldsymbol{p}^0_j + c \varDelta t \boldsymbol{v}^0_j \end{aligned}$$

(13)

where $\boldsymbol{p}^0_j$ and $\boldsymbol{v}^0_j$ are the current position and velocity of the $j^{th}$ neighboring robot.

The cost values of each node are calculated using the flocking heuristic functions. For the $i^{th}$ node at the $c^{th}$ level of the search tree, $\boldsymbol{p}_i$ and $\boldsymbol{v}_i$ are taken as the position and velocity states of the $i^{th}$ node whereas $\boldsymbol{p}_j$ taken as the predicted position of the $j^{th}$ neighboring robot at the $c^{th}$ level of the search tree.

For consistency with SFM, the inter-robot heuristic function is designated in the form of the spring potential energy function as:

$$\begin{aligned} \displaystyle h_{i}^{r} = \sum _{j=1}^{M} w^{r} \left( d_{ij} - d_{eq} \right) ^2 \end{aligned}$$

(14)

where $w^{r}$ is the inter-robot heuristic coefficient.

Similarly, the obstacle avoidance heuristic function is taken as the potential function of the obstacle avoidance force as:

$$\begin{aligned} \displaystyle h_{i}^{o} = \sum _{k=1}^{O} w^{o} \frac{1}{ d_{ik}} \end{aligned}$$

(15)

where $w^{o}$ is the obstacle avoidance heuristic coefficient.

The migration heuristic is taken as the combination of the speed and direction heuristic functions. The speed heuristic maintains the speed of the robots at migration speed, and the direction heuristic moves robots towards the migration direction. The speed and direction heuristics are calculated as:

$$\begin{aligned} \displaystyle h_{i}^{s} = w^{s} \big | \Vert \boldsymbol{v}_{mig}\Vert - \Vert \boldsymbol{v}_{i}\Vert \big |, \end{aligned}$$

(16)

$$\begin{aligned} \displaystyle h_{i}^{d} = w^{d} \left( 1 - \frac{\boldsymbol{v}_{mig} \cdot \boldsymbol{v}_i}{\Vert \boldsymbol{v}_{mig} \Vert \Vert \boldsymbol{v}_i \Vert } \right) \end{aligned}$$

(17)

where $w^{s}$ and $w^{d}$ are the speed and direction heuristic coefficients, respectively.

The sum of the inter-robot, obstacle avoidance, speed, and direction heuristics is calculated as:

$$\begin{aligned} \displaystyle h_{i}^{u} = h_{i}^{r} + h_{i}^{o} + h_{i}^{s} + h_{i}^{d}. \end{aligned}$$

(18)

The heuristic cost of the $i^{th}$ node is obtained as:

$$\begin{aligned} \displaystyle h_{i} = h_{i}^{u} + h_{i}^{p} \end{aligned}$$

(19)

where $h_{i}^{p}$ is the heuristic cost of the parent node of the $i^{th}$ node.

To find a trajectory that meets the flocking objectives, each robot utilizes a beam-search algorithm that expands only the $\beta$ number of nodes with the lowest heuristic cost at each level of the search tree and prunes the remaining nodes to reduce the required time and memory for the search. The total number of levels in the search tree, which determines the total number of predicted future steps, is called the depth, d. The starting node of the search tree is represented as node 0, whose states are the current position and velocity of the robot, and its heuristic cost is taken as $h_0=0$ since its value does not affect the search result. The trajectory of the node with the smallest heuristic cost at the $d^{th}$ level of the search tree is taken as the found trajectory. Each robot repeats the search process within a short time interval, $\varDelta t$, and takes its next velocity command as the first velocity state of the found trajectory, as illustrated in Fig. 2.

Fig. 3.

Simulated trajectories of (top) PFM and (bottom) SFM in (a) the first, (b) second, and (c) third environment. Videos are available at https://tinyurl.com/Giray22.

3 Experimental Setup

We prepared three test environments consisting of a $L \times L$ rectangular arena with cylindrical obstacles to compare SFM and PFM in kinematic simulations. The first environment has low obstacle density, the second environment has high obstacle density, and the third environment contains a wall consisting of intertwined obstacles (Fig. 3).

2D Gaussian noise ($\mu = 0, \sigma _n = 0.02$) is added to the positions and velocities of the robots to test the robustness of the models. At the beginning of each test, robots are randomly placed in the environment. The tests are completed when all robots cross the finish line at $y_f$, and the maximum time allowed to complete a test is limited to $t_{max}$. Each test is repeated 10 times.

To test the applicability of PFM on real robots, we used a swarm of six Crazyflie 2.1 quadcopters¹ in an indoor flight arena populated with obstacles and communicated with them using the Crazyswarm platform [12]. Positions of the quadcopters are tracked using the Vicon motion capture system, and the velocity commands are computed on a single computer in different threads to mimic the decentralized behavior.

The parameters used in simulation and real robot tests are provided in Tables 1 and 2.

The order, speed error, and proximity metrics are introduced based on previous work [15, 17] to evaluate the performance of the flocking models. The order metric measures the coherence of the heading directions of the neighboring robots:

$$\begin{aligned} \displaystyle \varTheta _{ord} = \sum _{i=1}^{N} \sum _{j=1}^{M} \frac{ \boldsymbol{v}_i \cdot \boldsymbol{v}_j }{N M \Vert \boldsymbol{v}_i \Vert \Vert \boldsymbol{v}_j \Vert }. \end{aligned}$$

(20)

$\varTheta _{ord}$ becomes 1 when the neighboring robots are perfectly aligned, and it becomes $-1$ in case of complete disorder.

The speed error metric measures the normalized mean difference between the speed of the robots and the desired migration speed:

$$\begin{aligned} \displaystyle E_{spd} = \sum _{i=1}^{N} \frac{\big | \Vert \boldsymbol{v}_{mig} \Vert - \Vert \boldsymbol{v}_{i} \Vert \big |}{N \Vert \boldsymbol{v}_{mig} \Vert }. \end{aligned}$$

(21)

$E_{spd}$ becomes 0 when the robots’ speed is equal to the migration speed, whereas its value gets larger when the difference between robots’ speed and migration speed increases.

Table 1. Parameters of PFM and SFM used in simulation and real robot tests.

Table 2. Common parameters that are used in both simulation and real robot tests.

The proximity metric measures the normalized mean distance between the robots and their neighbors:

$$\begin{aligned} \displaystyle D_{prox} = \sum _{i=1}^{N} \sum _{j=1}^{M} \frac{d_{ij}}{N M {d}_{eq}}. \end{aligned}$$

(22)

$D_{prox}$ becomes 1 when the mean inter-robot distance is equal to the equilibrium distance. Its value decreases as the robots get closer to each other and increases as they move away from each other.

Fig. 4.

(a) The order, (b) speed error, and (c) proximity metric values of PFM and SFM for the 10 times repeated tests in three different environments. Colored regions illustrate the data distribution, and white dots within the colored regions represent the median values.

4 Results and Discussion

The metric values of simulation tests for PFM and SFM in three different environments are depicted in Fig. 4 as violin plots. In violin plots, the first 0.5 seconds of each test are excluded in order to eliminate the initial transient period. PFM has order values close to 1 in all environments, whereas the order values of SFM decreased significantly in the second and third environments compared to the first one due to the change in environmental conditions (Fig. 4a). The effect of environmental change is further evident in the speed error metric; PFM has almost zero speed error values, whereas the SFM has significantly large speed error values in all environments (Fig. 4b). In the third environment, SFM only completed half of the tests within the maximum allowed time, $t_{max}$, and completed the remaining ones 3 to 6 times slower than PFM because of the highly reduced speed of the robots around the obstacle boundary. The performance of PFM and SFM is close in terms of cohesion; both models kept the proximity values close to 1 in all environments (Fig. 4c), and no collisions were observed throughout the tests.

Fig. 5.

(a) The order, (b) normalized speed, and (c) normalized inter-robot distance of (top) PFM and (bottom) SFM in the second environment. The plots are grey-scaled from the time PFM completes the task. In (b) and (c), solid lines are the mean values of the normalized speed and normalized inter-robot distance, whereas shades represent the maximum and minimum values. (Color figure online)

Fig. 6.

(a) Trajectories of the quadcopters, (b) the order, (c) normalized speed, (d) normalized inter-robot distance of PFM in a real robot test, and (e) Crazyflie 2.1 quadcopter. In (c) and (d), solid lines are the mean values of the normalized speed and normalized inter-robot distance, whereas shades represent the maximum and minimum values. Video is available at https://tinyurl.com/Giray22.

For a more detailed comparison of PFM and SFM, trajectories of robots in three environments with the same initial positions are given in Fig. 3. While both models have smooth trajectories in the first environment (Fig. 3a), the trajectories of SFM are distorted near obstacle boundaries in the second and third environments (Fig. 3b, c). The order, normalized speed, and normalized inter-robot distance plots for both models in the second environment are given in Fig. 5. PFM completed the test faster than SFM by performing more ordered motion (Fig. 5a) and tracking the migration speed much better (Fig. 5b) while maintaining the mean inter-robot distance close to the equilibrium distance (Fig. 5c).

The results of the real robot test are given in Fig. 6. Similar to simulation tests, PFM completed the real robot test with nearly perfect order values (Fig. 6b) by tracking the migration speed with small errors (Fig. 6c) while keeping the mean inter-robot distance around the equilibrium distance (Fig. 6d).

Results of the tests showed that SFM might lead to oscillatory flocking behavior in cluttered environments due to its reactivity, and this behavior has a negative impact on the coherence of the robot swarm. Moreover, it is observed that the short-sightedness of SFM may cause robots to get stuck in obstacles and swarm speed to slow down drastically. On the other hand, it has been shown that PFM can achieve coherent flocking motion at desired migration speed in different environments by allowing the robot swarm to move according to predicted future states.

In this work, it is assumed that robots can only sense the closest point on the boundary of an obstacle. Since planning long-range trajectories without knowing the exact positions and shapes of the obstacles may be misleading, the depth of the search tree is kept small. Furthermore, it is observed that increasing the value of $\beta$ does not improve the flocking behavior significantly for small depth values. Therefore, small $\beta$ and d values are used in both simulation and real robot tests, reducing the required time for the trajectory search. Planning short-range trajectories also let robots use the constant velocity assumption for their neighbors, simplifying the prediction process and reducing the computational cost of PFM.

5 Conclusion

In this study, we proposed a novel search-based predictive flocking model (PFM) that only depends on local information of the neighboring robots and the environment. We compared PFM with the virtual force-based standard flocking model (SFM) in different environments based on order, speed error, and proximity metrics. Results showed that the proposed PFM could perform successful flocking behavior despite environmental differences, unlike SFM. We tested the applicability of PFM on real robots with a swarm of six quadcopters in a cluttered flight arena and validated that PFM works successfully with robot swarms as in simulation. Future work will include the dynamic obstacle avoidance and the application of the search-based prediction model for other collective behaviors such as aggregation and foraging.