Uncertainty Quantification in Depth Estimation via Constrained Ordinal Regression

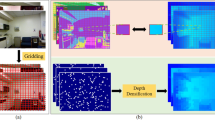
Abstract

Monocular Depth Estimation (MDE) is a task to predict a dense depth map from a single image. Despite the recent progress brought by deep learning, existing methods are still prone to errors due to the ill-posed nature of MDE. Hence depth estimation systems must be self-aware of possible mistakes to avoid disastrous consequences. This paper provides an uncertainty quantification method for supervised MDE models. From a frequentist view, we capture the uncertainty by predictive variance that consists of two terms: error variance and estimation variance. The former represents the noise of a depth value, and the latter measures the randomness in the depth regression model due to training on finite data. To estimate error variance, we perform constrained ordinal regression (ConOR) on discretized depth to estimate the conditional distribution of depth given image, and then compute the corresponding conditional mean and variance as the predicted depth and error variance estimator, respectively. Our work also leverages bootstrapping methods to infer estimation variance from re-sampled data. We perform experiments on both simulated and real data to validate the effectiveness of the proposed method. The results show that our approach produces accurate uncertainty estimates while maintaining high depth prediction accuracy. The code is available at https://github.com/timmy11hu/ConOR

1 Introduction

Estimating depth from 2D images has received much attention due to its vital role in various vision applications, such as autonomous driving [15] and augmented reality [41]. In the past decade, a variety of works have successfully addressed MDE by using supervised and self-supervised approaches [6, 18, 19, 24, 50, 54, 57, 78]. Yet, the ill-posed nature of the task leads to more uncertainty in the depth distribution, resulting in error-prone models. In practice, overconfident incorrect predictions can be harmful or offensive; hence it is crucial for depth estimation algorithms to be self-aware of possible errors and provide trustworthy uncertainty information to assist decision making.

Fig. 1.

From a single input image (1a) we estimate depth (1b) and uncertainty (1d) maps. (1c) is the actual error as the difference between (1b) and ground truth. The black parts do not have ground truth depth value

This work aims to estimate the uncertainty of a supervised single-image depth prediction model. From a frequentist perspective, we quantify the uncertainty of depth prediction by using the predictive variance, which can be decomposed into two terms: (i) error variance and (ii) estimation variance. Error variance describes the inherent uncertainty of the data, i.e. depth variations that the input image cannot explain, also known as aleatoric uncertainty [37]. Estimation variance arises from the randomness of the network parameters caused by training on finite data, which is conventionally called epistemic uncertainty [37].

One straightforward method to estimate the error variance is to predict the conditional variance as well as the expected depth value by optimizing the heteroskedastic Gaussian Likelihood (GL) with input-dependent variance parameters [65]. However, this approach often leads to unstable and slow training due to the potentially small variances for specific inputs. Moreover, directly regressing depth value on the input images has been shown sub-optimal prediction performance [6, 24, 25]. Alternatively, Yang et al. formulate MDE as a classification problem and measure the uncertainty by Shannon entropy [86]. However, the classification model also leads to sub-optimal prediction performance due to ignorance of the ordinal relation in depth. Moreover, there is a gap between Shannon entropy and the uncertainty of the regression model.

To estimate the error variance without sacrificing the prediction accuracy, we base our work on the deep ordinal regression (OR) model [24]. The original OR model was trained on discretized depth values with ordinal regression loss, which showed a significant boost in prediction accuracy compared to vanilla regression approaches. However, due to the discretization of depth, an optimal method to estimate the error variance for this model remains elusive. To tackle this problem, we take the advantage of the recent progress on distributional regression [54] to learn a likelihood-free conditional distribution by performing constrained ordinal regression (ConOR) on the discretized depth values. Compared to OR [24], ConOR guarantees the learning of conditional distributions of the original continuous depth given input images. Thus, we can take the expectation from the conditional distribution estimator as predicted depth, and the variance as the estimate of error variance.

Estimation variance is a long-standing problem in statistics and machine learning. If the model is simple, e.g. a linear model, one could easily construct confidence intervals of the parameters via asymptotic analysis. In our case, as the asymptotic theory for deep neural networks is still elusive, we leverage the idea of bootstrap to approximate the estimation variance by the sample variance of depth estimation calculated from re-sampled datasets. More specifically, we utilize two types of re-sampling schemes: Wild Bootstrap [84] (WBS) and Multiplier Bootstrap [10] (MBS). While the WBS performs re-weighting on the residuals to generate resamples, the MBS samples the weights that act as a multiplier of the training loss. To speed up training, we first train a single model on the entire training set and use the model parameters as initialization for training the bootstrap models. We evaluate our proposed method on both simulated and real datasets, using various metrics to demonstrate the effectiveness of our approach. Figure 1 shows the masked output of our uncertainty estimator, against the mistake made by our predicted depth.

2 Related Work

Monocular Depth Estimation. Early MDE approaches tackle the problem by applying hand-handcrafted filters to extract features [3, 11, 26, 34, 47, 49, 55, 69, 73, 74, 76, 88]. Since those features alone can only capture the local information, a Markov Random Field model is often trained in a supervised manner to estimate the depth value. Thanks to representation learning power of CNNs, recent approaches design various neural network architectures to estimate depth in an end-to-end manner [2, 4, 18, 19, 38, 50, 52, 53, 57, 63, 72, 75, 82, 87]. Eigen et al. [19] formulate the problem as a supervised regression problem and propose a multi-scale network architecture. By applying recent progress in CNN technology, Laina et al. [50] solve the problem by using a reverse Huber loss and train a fully convolutional residual network with up-convolutional blocks to increase the output resolution. Cao et al. [6] address the problem as a classification problem and use a fully connected Conditional Random Fields to smooth the depth estimation. To utilize the ordinal nature of the discretized depth class, Fu et al. [24] formulate the problem as ordinal regression [23], and use a standard encoder-decoder architecture to get rid of previous costly up-sampling techniques. Their network consists of multiple heads, and each head solves a independent binary classification problem whether a pixel is either closer or further away from a certain depth threshold. However, the network does not output a valid distribution since the probabilities across the thresholds are not guaranteed to be monotonic.

Aside from supervised learning, many works try to eliminate the need for labeled data, as depth sensors are usually needed to obtain groundtruth depth. One direction is to use self-supervised learning, which takes a pair of images and estimate a disparity map for one of the images as an intermediate step to minimize the reconstruction loss [29, 32, 70, 71, 81, 89]. Another direction is to consider depth estimation problem in a weakly-supervised manner by estimating the relative depth instead of the absolute metric value [7, 9, 25, 56, 61, 85, 90].

Uncertainty Quantification via Bayesian Inference. Uncertainty quantification is a fundamental problem in machine learning. There is a growing interest in quantifying the uncertainty of deep neural networks via Bayesian neural networks [8, 43, 58, 83], as the Bayesian posterior naturally captures uncertainty. Despite the effectiveness in representing uncertainty, computation of the exact posterior is intractable in Bayesian deep neural networks. As a result, one must resort to approximate inference techniques, such as Markov Chain Monte Carlo [8, 16, 48, 59, 62, 64] and Variational Inference [5, 13, 14, 22, 31, 40, 45, 79]. To reduce computational complexity, Deep Ensemble [36, 51] (DE) is proposed to sample multiple models as from the posterior distribution of network weights to estimate model uncertainty. In addition, the connection between Dropout and Bayesian inference is explored and results in the Monte Carlo Dropout [27, 28] (MCD). Despite its efficiency, [21] points out that MCD changes the original Bayesian model; thus cannot be considered as approximate Bayesian inference.

Distributional Regression. Over the past few years, there has been increasing interest in distributional regression, which captures aspects of the response distribution beyond the mean [17, 35, 46, 60, 66, 68]. Recently, Li et al. [54] propose a two-stage framework that estimates the conditional cumulative density function (CDF) of the response in neural networks. Their approach randomly discretizes the response space and obtains a finely discretized conditional distribution by combining an ensemble of random partition estimators. However, this method is not scalable to the deep CNNs used in MDE. Therefore, we modify their method to obtain a well-grounded conditional distribution estimator by using one single network with the Spacing-Increasing Discretization [24].

3 Method

To illustrate our method, we first show our formulation of the uncertainty as predictive variance and decompose it into error variance and estimation variance. We then introduce how to make prediction and estimate error variance via learning a conditional probability mass function (PMF) from a constrained ordinal regression (ConOR). Finally, we discuss how we infer estimation variance using re-sampling methods. Figure 2 demonstrate a brief idea of the training and testing phase of our method.

3.1 Uncertainty as Predictive Variance

Variance is commonly used in machine learning to measure uncertainty, which describes how far a set of real observations is dispersed from the expected value. To quantify how much uncertainty is in the depth prediction, for simplicity let us consider the depth prediction network as a general location-scale model [20]. We then formulate the model as:

$$\begin{aligned} y_i = g(x_i) + \sqrt{V(x_i)}\epsilon _i, \ \ \ \text {for } i = 1,\dots ,n, \end{aligned}$$

(1)

where $x_i, y_i$ denote the feature and the response variable respectively, g(x) stands for the mean function, $\epsilon _i$ represents the random errors with zero mean and unit variance, and V(x) denotes the variance function. Suppose $\hat{g}$ is an estimator of g based on the training observations $\{(x_i,y_i)\}_{i=1}^{n}$. With $x_{*}$ as a new input, the corresponding unknown response value is

$$\begin{aligned} y_* = g(x_*) + \sqrt{V(x_*)}\epsilon _*, \end{aligned}$$

(2)

where $\epsilon _*$ is a random variable with zero mean and unit variance. Given the estimator $\hat{g}$, the value of $y_*$ is predicted by $\hat{y}_* = \hat{g}(x_*)$, thus the predictive variance can be written as:

$$\begin{aligned} \textrm{Var}\left[ y_* - \hat{y}_*\right] = Var \left[ g(x_*) + \sqrt{V(x_*)}\epsilon _* -\hat{g}(x_*)\right] . \end{aligned}$$

(3)

Since $y_*$ is a new observation and $\hat{g}$ only depends on the training observations ${\{(x_i, y_i)\}}_{i=1}^n$, the random noise $\epsilon _*$ and $\hat{g}$ can be seen as independent. This gives

$$\begin{aligned} Var \left[ y_* - \hat{y}_*\right] = \underbrace{V(x_*)}_{\text {error variance}} + \underbrace{Var \left[ \hat{g}(x_*)\right] }_{\text {estimation variance}}. \end{aligned}$$

(4)

The first component is known as error variance [12], and we refer to the second component as the estimation variance. Therefore, one can estimate two terms separately and quantify the total uncertainty by the summation of two terms. In the following sections, we present how to obtain their empirical estimators $\hat{V}(x_*)$ and $\widehat{Var }\left[ \hat{g}(x_*)\right]$.

Fig. 2.

Our approach first uses an encoder-decoder network $\varPhi$ to extract pixel-wise features $\eta _i^{(w,h)}$ from input image $x_i$, and output the conditional PMF. During training, we obtain conditional CDF and construct an ordinal regression loss with the ground truth depth. In the test phase, we compute the expectation and variance from the conditional PMF estimator as depth prediction and error variance

3.2 Constrained Ordinal Regression

Discretization. To learn a likelihood-free distribution, we first discretize continuous depth into discrete categories with ordinal nature. Considering that computer vision systems as well as humans are less capable of making precise prediction for large depths, we apply the Spacing-Increasing Discretization (SID) [24, 25], which partitions the range of depth $[\alpha , \beta ]$ uniformly on the log space by $K+1$ thresholds $t_0<t_{1}< t_{2}< \dots < t_{K}$ into K bins, where

$$\begin{aligned} t_k = \exp \left[ \log {\left( \alpha \right) }+k\log {\left( \beta /\alpha \right) }/K \right] \text {, for } k\in \{0,1,\dots ,K\}. \end{aligned}$$

(5)

Let $B_k =(t_{k-1}, t_k]$ denote the kth bin, for $k\in \{1,2,\dots ,K\}$, we recast the problem to a discrete classification task that predicts the probability of pixel’s depth falling into each bin. Let $x_i$ denote an image of size $W\times {H}\times {C}$ and $\varPhi$ indicate a feature extractor. The $W\times {H}\times {K}$ feature map obtained from the network can be written as $\eta _i=\varPhi (x_i)$, and $\eta _i^{(w,h)}$ points to the features of (w, h) pixel. The conditional PMF, probabilities that $Y_i^{(w,h)}$ belongs to the kth bin, can be predicted by feeding K-dimensional feature $\eta _i^{(w,h)}$ into a softmax layer:

$$\begin{aligned} P \left( Y_i^{(w,h)} \in B_k|\varPhi (x_i)\right) = \frac{e^{\eta _{i,k}^{(w,h)}}}{\varSigma _{j=1}^{K}{e^{\eta ^{(w,h)}_{i,j}}}}, \text { for } k\in \{1,2,\dots ,K\}, \end{aligned}$$

(6)

where $\eta _{i,k}^{(w,h)}$ represents the kth element of $\eta _i^{(w,h)}$ (also known as logits). The softmax normalization ensures the validity of output conditional distributions.

Learning. During the training, to incorporate the essential ordinal relationships among the discretized classes into the supervision, we obtain the conditional CDF in a staircase form by cumulatively summing the value of conditional PMF:

$$\begin{aligned} P \left( Y_i^{(w,h)} \le t_k |\varPhi (x_i)\right) = \sum _{j=1}^{k} P \left( Y_i^{(w,h)} \in B_j|\varPhi (x_i)\right) ,\text { for } k\in \{1,2,\dots ,K\}. \end{aligned}$$

(7)

This can be regarded as the probabilities of $Y_i^{(w,h)}$ less than or equal to the kth threshold. Given the ground truth depth value $y_i^{(w,h)}$, we construct an ordinal regression loss by solving a pixel-wise binary classification across K thresholds:

$$\begin{aligned} \ell \left( x_i,y_i^{(w,h)},\varPhi \right) = - \sum _{k=1}^K \Big \{ \mathbbm {1}\left( y_i^{(w,h)} \le t_k\right) \log \left( P (Y_i^{(w,h)} \le t_k |\varPhi (x_i))\right) \\ + \left[ 1-\mathbbm {1}\left( y_i^{(w,h)} \le t_k\right) \right] \left[ 1-\log \left( P (Y_i^{(w,h)} \le t_k |\varPhi (x_i))\right) \right] \Big \} , \end{aligned}$$

(8)

where $\mathbbm {1}$ is the indicator function. We optimize the network to minimize the ordinal regression loss over all the training examples with respective to $\varPhi$:

$$\begin{aligned} \mathcal {L}\left( \varPhi \right) = \sum _{i=1}^n \sum _{w=1}^W \sum _{h=1}^H \ell \left( x_i,y_i^{(w,h)},\varPhi \right) . \end{aligned}$$

(9)

Prediction. After training, we obtain an estimator $\hat{\varPhi }={{\,\textrm{argmin}\,}}_\varPhi \mathcal {L}\left( \varPhi \right)$ . In the test phase, considering the multi-modal nature of the predicted distribution, given a new image $x_*$, for each pixel, we take the expectation of the conditional PMF as our prediction:

$$\begin{aligned} \hat{g}^{(w,h)}(x_*) = E \left[ Y_*^{(w,h)}| x_*;\hat{\varPhi }\right] = \sum _{k=1}^K \mu _k P \left( Y_*^{(w,h)} \in B_k|\hat{\varPhi }(x_*)\right) , \end{aligned}$$

(10)

where $\mu _k = (t_{k-1}+t_k)/2$ is the expected value of kth bin. This gives a smoother depth prediction, compared to the hard bin assignment used by [24]. More importantly, the expected value suits well the following uncertainty inference using variance.

3.3 Error Variance Inference

The inherent variability of response value $Y_*^{(w,h)}$ comes from the noisy nature of the data, which is irreducible due to the randomness in the real world. While the expected value describes the central tendency of the depth distribution, the variance can provide information about the spread of predicted probability mass. Thus we use the variance from estimated conditional PMF to infer the variance of the response error:

$$\begin{aligned} \widehat{V}^{(w,h)}(x_*)&= Var \left[ Y_*^{(w,h)}| x_*;\hat{\varPhi } \right] \end{aligned}$$

(11)

$$\begin{aligned}&= \sum _{k=1}^K { \left( \mu _k - E \left[ Y_*^{(w,h)}| x_*;\hat{\varPhi }\right] \right) }^2 P \left( Y_*^{(w,h)} \in B_k|\hat{\varPhi }(x_*) \right) . \end{aligned}$$

(12)

Hence our ConOR can predict the depth value together with error variance in the test phase.

3.4 Estimation Variance Inference

The second component, estimation variance, represents the discrepancy of our model prediction $E \big [Y_*^{(w,h)}\mid x_*;\hat{\varPhi }\big ]$, which is usually caused by finite knowledge of training observations $\mathcal {D}$. Ideally, if we have the access to the entire population, given a model class $\varPhi$ and M i.i.d. datasets $\{\mathcal {D}_m\}_{m=1}^M$, we can have M independent empirical estimators:

$$\begin{aligned} \hat{\varPhi }_m = \mathop {{{\,\textrm{argmin}\,}}}_\varPhi \sum _{i=1}^n \sum _{w=1}^W \sum _{h=1}^H \ell \left( x_{m,i},y_{m,i}^{(w,h)},\varPhi \right) , \text { for } m = 1,2,\dots ,M, \end{aligned}$$

(13)

where $(x_{m,i}, y_{m,i})$ represents ith training pair in $\mathcal {D}_m$. Then the estimation variance $Var \big [E [Y_*^{(w,h)}|x_*;\hat{\varPhi }]\big ]$ could be approximated by the sample variance of prediction from different estimators:

$$\begin{aligned} \frac{1}{M-1}\sum _{m=1}^M{\left( E \left[ Y_*^{(w,h)}|x_*;\hat{\varPhi }_m\right] - \frac{1}{M}\sum _{j=1}^M{E \left[ Y_*^{(w,h)}|x_*;\hat{\varPhi }_j\right] }\right) }^2. \end{aligned}$$

(14)

However in practice, we cannot compute the estimation variance as we do not have a large number of datasets from the population. To address this problem, we adapt re-sampling methods. As a frequentist inference technique, bootstrapping a regression model gives insight into the empirical distribution of a function of the model parameters [84]. In our case, the predicted depth can be seen as a function of the network parameters. Thus we use the idea of bootstrap to achieve M empirical estimators $\{\hat{\varPhi }_m\}_{m=1}^M$ and then use them to approximate $Var \big [E [Y_*^{(w,h)}|x_*;\hat{\varPhi }]\big ]$. To speed up training, we initialize the M models with the parameters of the single pre-trained model for prediction and error variance estimation. We discuss the details of the re-sampling approaches below.

Wild Bootstrap (WBS). The idea of Wild Bootstrap proposed by Wu et al. [84] is to keep the inputs $x_i$ at their original value but re-sample the response variable $y_i^{(w,h)}$ based on the residuals values. Given $\hat{y}_i^{(w,h)} = E [Y_i^{(w,h)}|x_i;\hat{\varPhi }]$ as the fitted value, and $\hat{\epsilon }_i^{(w,h)} = y_i^{(w,h)} - \hat{y}_i^{(w,h)}$ as the residual, we re-sample a new response value for mth replicate based on

$$\begin{aligned} \upsilon _{m,i}^{(w,h)}=\hat{y}_i^{(w,h)} + \hat{\epsilon }_i^{(w,h)}\cdot \tau _{m,i}^{(w,h)}, \end{aligned}$$

(15)

where $\tau _{m,i}^{(w,h)}$ is sampled from standard Gaussian distribution. For each replicate, we train the model on the new sampled training set:

$$\begin{aligned} \hat{\varPhi }_m = \mathop {{{\,\textrm{argmin}\,}}}_\varPhi \sum _{i=1}^n \sum _{w=1}^W \sum _{h=1}^H \ell \left( x_{i},\upsilon _{m,i}^{(w,h)},\varPhi \right) , \text { for } m = 1,2,\dots ,M, \end{aligned}$$

(16)

The overall procedure is outlined in Supplementary Material (SM) Sect. 1.

Multiplier Bootstrap (MBS). The idea the Multiplier Bootstrap [80] is to sample different weights used to multiply the individual loss of each observation. Here, we maintain the value of training data but re-construct the loss function for the mth replicate by putting different sampled weights across observations:

$$\begin{aligned} \hat{\varPhi }_m = \mathop {{{\,\textrm{argmin}\,}}}_\varPhi \sum _{i=1}^n \sum _{w=1}^W \sum _{h=1}^H \omega _i^{(w,h)} \ell (x_i,y_i^{(w,h)},\varPhi ), \text { for } m = 1,2,\dots ,M, \end{aligned}$$

(17)

where $\omega _i^{(w,h)}$ is the weight sampled from Gaussian distribution with unit mean and unit variance. Details are given in SM Sect. 1.

4 Experiment

To verify the validity of our method, we first conduct intuitive simulation experiments on toy datasets, by which we straightly compare our estimated uncertainty with the ground truth value. The qualitative and quantitative results can be found in SM Sect. 2. In this section, we evaluate on two real datasets, i.e., KITTI [30] and NYUv2 [77]. Some ablation studies are performed to give more detailed insights into our method.

4.1 Datasets

KITTI. The KITTI dataset [30] contains outdoor scenes (1–80 m) captured by the cameras and depth sensors in a driving vehicle. We follow Eigen’s split [19] for training and testing, where the train set contains 23,488 images from 32 scenes and the test set has 697 images. The ground-truth depth maps improved from raw LIDAR are used for learning and evaluating. We train our model on a random crop of size $370\times 1224$ and evaluate the result on a center crop of the same size with the depth range of 1 m to 80 m.

NYUv2. The NYU Depth v2 [77] dataset consists of video sequences from a variety of indoor scenes (0.5–10 m) and depth maps taken from the Microsoft Kinect. Following previous works [1, 4], we train the models using a 50K subset, and test on the official 694 test images. The models are trained on a random crop size of $440\times 590$ and tested based on the pre-defined center crop by [19] with the depth range of 0 m to 10 m.

4.2 Evaluation Metrics

The evaluation metrics of the depth prediction follow the previous works [19, 57]. For the comparison of uncertainty estimation, as there is no ground truth label, we follow the idea of sparsification error [39]. That is, when pixels with the highest uncertainty are removed progressively, the error should decrease monotonically. Therefore, given an error metric $\xi$, we iteratively remove a subset ($1\%$) of pixels according to the descending order of estimated uncertainty and compute $\xi$ on the remaining pixels to plot a curve. An ideal sparsification (oracle) is obtained by sorting pixels in descending order of true errors; hence we measure the difference between estimated and oracle sparsification by the Area Under the Sparsification Error (AUSE) [39]. We also calculate the Area Under the Random Gain (AURG) [67], which measures the difference between the estimated sparsification and a random sparsification without uncertainty modelling. We adopt root mean square error (rmse), absolute relative error (rel), and $1-\delta _1$ as $\xi$. Both AUSE and AURG are normalized over the considered metrics to eliminate the factor of prediction accuracy, for the sake of fair comparison [39].

4.3 Implementation Details

We use ResNet-101 [33] and the encoder-decoder architecture proposed in [24] as our network backbone. We add a shift $\gamma$ to both $\alpha$ and $\beta$ so that $\alpha + \gamma = 1.0$, then apply SID on $\left[ \alpha + \gamma , \beta + \gamma \right]$. We set $\alpha , \beta , \gamma$ to 1, 80, 0 for KITTI [30] and 0, 10, 1 for NYUv2 [77]. The batch size is set to 4 for KITTI [30] and 8 for NYUv2 [77]. The networks are optimized using Adam [44] with a learning rate of 0.0001 and trained for 10 epochs. We set our bootstrapping number to 20. To save computational time, we finetune the bootstrapping model for two epochs from the pre-trained model. This speedup yields only a subtle effect on the result.

For comparison, we implement Gaussian Likelihood (GL) and Log Gaussian Likelihood (LGL) for estimating the error variance and apply Monte Carlo Dropout (MCD) [28] and Deep Ensemble (DE) [51] for approximating estimation variance. Following previous works [42, 51], we adapt MCD [28] and DE [51] on GL and LGL, which is designed under Bayesian framework. We also implement Gaussian and Log Gaussian in our framework with WBS and MBS. We incorporate a further comparison to the other methods that model the uncertainty on supervised monocular depth prediction, including Multiclass Classification [6, 25] (MCC) and Binary Classification [86] (BC), applying the same depth discretization strategy as ours. Using softmax confidence (MCC) and entropy (BC) is generally seen as a total uncertainty [37], thus they are not adapted in any framework. We make sure the re-implemented models for comparison have an identical architecture to ours but only with a different prediction head.

4.4 Results

Table 1 and Table 2 give the results on KITTI [30] and NYUv2 [77], respectively. Here we only show three standard metrics of depth evaluation, more details can be found in SM Sect. 3.1. We put the plots of the parsification curve in SM Sect. 3.2. Firstly, our methods achieve the best result on the depth prediction in terms of all the metrics. Secondly, our methods outperform others in both AUSE and AURG. This strongly suggests that our predicted uncertainty has a better understanding of the error our model would make. The results show our method applies to both indoor and outdoor scenarios. Qualitative results are illustrated in Fig. 3 and Fig. 4, more results can be found in SM Sect. 3.3.

Table 1. Performance on KITTI

Fig. 3.

Depth prediction and uncertainty estimation on KITTI using ConOR and MBS. The masked variance is obtained from predictive variance. The black parts do not have ground truth depth in KITTI. Navy blue and crimson indicate lower and higher values respectively (Color figure online)

Table 2. Performance on NYUv2

Fig. 4.

Depth prediction and uncertainty estimation on NYUv2 using ConOR and WBS. Navy blue and crimson indicate lower and higher values respectively (Color figure online)

4.5 Ablation Studies

In this section, we study the effectiveness of modelling the error variance and the estimation variance. We first inspect the dominant uncertainty in our predictive variance, then illustrate the advantage of ConOR and analyze the performance between bootstrapping and previous Bayesian approaches. Lastly, we perform a sensitivity study of ConOR on KITTI [30].

Dominant Uncertainty. The uncertainty evaluation of our proposed method is based on the estimated predictive variance, which is composed of error variance and estimation variance. Table 3 reports the performance of uncertainty evaluation by applying different variances. We can notice that using predictive variance can achieve the best performance on AUSE and AURG for both datasets. In the predictive variance, the error variance is more influential than the estimation variance since its individual score is significantly close to the final scores of predictive variance. This indicates that the error variance estimated by ConOR (aleatoric uncertainty) can already explain most of the predictive uncertainty, and our approach can further enhance the uncertainty understanding using re-sampling methods. This result is reasonable because the large sample size of KITTI [30] and NYUv2 [77] training set leads to low estimation variance.

Table 3. Comparison of uncertainty evaluation on ConOR applying different variance

ConOR. We then conduct a comparison between ConOR and other methods that capture the error variance. We also re-implement OR [25] for contrast by taking the variance from the estimated distribution. Although we observe the invalid CDFs from the OR model, our purpose is to investigate how the performance is affected by the ill-grounded distribution estimator. Table 4 shows that ConOR yields the best performance in terms of both depth prediction and uncertainty estimation. Moreover, ConOR surpasses OR by a large margin on the uncertainty evaluation, which indicates the significance to make statistical inference based on a valid conditional distribution.

Table 4. Performance of different models for depth and error variance estimation

Bootstrapping. To analyze the strength of bootstrapping methods, we also apply ConOR under other frameworks i.e. MCD [28] and DE [51]. From Table 5 we can conclude that, compared to the baseline ConOR, MCD [28] does not provide correct estimation variance as the performance of uncertainty evaluation slightly decreases. DE [51] can improve some of the metrics for the uncertainty estimation. By using bootstrapping methods our predictive variance learns a better estimation variance approximation since all the metrics of uncertainty estimation have been boosted.

Table 5. Comparison of different methods to capture the estimation variance of ConOR

Discretization. To examine the sensitivity of ConOR to the discretization strategy, we compare SID with another common scheme, uniform discretization (UD), and apply the partition with a various number of bins. In Fig. 5, we can see that SID can improve the performance of both prediction and uncertainty estimation on ConOR. In addition, ConOR is robust to a large span of bin numbers regarding the prediction accuracy since the rmse ranges between 2.7 and 2.8 (orange line in Fig. 5a). We also find that increasing the number of bins tends to boost the performance of uncertainty estimation (Fig. 5b and 5c) due to a more finely-discretized distribution estimator. However, excessively increasing the bin number leads to diminishing returns but adds more computational burden. Hence, it is better to fit more bins within the computational budget.

Fig. 5.

Performance of UD and SID with a range of different bin numbers on KITTI (Color figure online)

5 Conclusions

In this paper, we have explored uncertainty modelling in supervised monocular depth estimation from a frequentist perspective. We have proposed a framework to quantify the uncertainty of depth prediction models by predictive variance which can be estimated by the aggregation of error variance and estimation variance. Moreover, we have developed a method to predict the depth value and error variance using a conditional distribution estimator learned from the constrained ordinal regression (ConOR) and approximated the estimation variance by performing bootstrapping on our model. Our approach has shown promising performance regarding both uncertainty and prediction accuracy.