Relative Pose from SIFT Features

Abstract

This paper derives the geometric relationship of epipolar geometry and orientation- and scale-covariant, e.g., SIFT, features. We derive a new linear constraint relating the unknown elements of the fundamental matrix and the orientation and scale. This equation can be used together with the well-known epipolar constraint to, e.g., estimate the fundamental matrix from four SIFT correspondences, essential matrix from three, and to solve the semi-calibrated case from three correspondences. Requiring fewer correspondences than the well-known point-based approaches (e.g., 5PT, 6PT and 7PT solvers) for epipolar geometry estimation makes RANSAC-like randomized robust estimation significantly faster. The proposed constraint is tested on a number of problems in a synthetic environment and on publicly available real-world datasets on more than 800 00 image pairs. It is superior to the state-of-the-art in terms of processing time while often leading more accurate results. The solvers are included in GC-RANSAC at https://github.com/danini/graph-cut-ransac.

1 Introduction

This paper addresses the problem of interpreting orientation- and scale-covariant features, e.g. SIFT [23] or SURF [13], w.r.t. the epipolar geometry characterized either by a fundamental or an essential matrix. The derived relationship is then exploited to design minimal relative pose solvers that allow significantly faster robust estimation than by using the traditional point-based solvers.

Nowadays, a number of algorithms exist for estimating or approximating geometric models, e.g., homographies, using fully affine-covariant features. Some methods [31, 36] approximate the epipolar geometry from one or two affine correspondences by converting them to point pairs. Bentolila et al. [14] proposed a solution for estimating the fundamental matrix using three affine features. Raposo et al. [34, 35] and Barath et al. [9] showed that two correspondences are enough for estimating the relative pose when having calibrated cameras. Moreover, two correspondences are enough for solving the semi-calibrated case, i.e., when the objective is to find the essential matrix and a common unknown focal length [6]. Guan et al. [16] proposed ways of estimating the generalized pose from affine correspondences. Also, homographies can be estimated from two affine correspondences as shown in the dissertation of Kevin Koser [19], and, in the case of known epipolar geometry, from a single correspondence [4]. There is a one-to-one relationship between local affine transformations and surface normals [11, 19]. Pritts et al. [32, 33] showed that the lens distortion parameters can be retrieved using affine features. The ways of using such solvers in practice are discussed in [12].

Affine correspondences encode higher-order information about the underlying the scene geometry. This is why the previously mentioned methods solve geometric estimation problems (e.g., homographies and epipolar geometry) using only a few correspondences – significantly fewer than what point-based methods need. However, requiring affine features implies their major drawback. Detectors for obtaining accurate affine correspondences, for example, Affine-SIFT [29], Hessian-Affine or Harris-Affine [24], MODS [26], HesAffNet [27], are slow compared to other detectors. Therefore, they are not applicable in time-sensitive applications, where real-time performance is required.

In this paper, the objective is to bridge this problem by exploiting partially affine covariant features. The typically used detectors (e.g., SIFT and ORB) obtain more information than simply the coordinates of the feature points, for example, the orientation and scale. Even though this information is actually available “for free”, it is ignored in point-based solvers. We focus on exploiting this already available information without requiring additional computations, e.g., to extract expensive affine features.

Fig. 1.

Example image pairs from the PhotoTourism [3] and KITTI [15] datasets where the proposed SIFT-based solver estimates the (a) fundamental and (b) essential matrix and (c) solves the semi-calibrated case (i.e., unknown focal length). A hundred random inliers are drawn.

Using partially affine covariant features for model estimation is a known approach with a number of papers published in the recent years. In [25], the feature orientations are used to estimate the essential matrix. In [1], the fundamental matrix is assumed to be a priori known and an algorithm is proposed for approximating a homography exploiting the rotations and scales of two SIFT correspondences. The approximative nature comes from the assumption that the scales along the axes are equal to the SIFT scale and the shear is zero. In general, these assumptions do not hold. The method of Barath et al. [7] approximates the fundamental matrix by enforcing the geometric constraints of affine correspondences on the epipolar lines. Nevertheless, due to using the same affine model as in [1], the estimated epipolar geometry is solely an approximation.

Fig. 2.

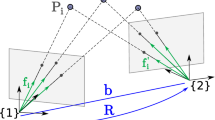
(a) The geometric interpretation of the relationship of a local affine transformations and the epipolar geometry (Eq. (6); proposed in [6]). Given the projection $\textbf{p}_i$ of point $\textbf{P}$ in the ith camera $\textbf{K}_i$, $i \in \{1,2\}$. The normal $\textbf{n}_1$ of epipolar line $\textbf{l}_1$ is mapped by affinity $\textbf{A}\in \mathbb {R}^{2 \times 2}$ into the normal $\textbf{n}_2$ of epipolar line $\textbf{l}_2$. (b) Visualization of the orientation- and scale-covariant features. Point ${\textbf {P}}$ and the surrounding patch projected into cameras ${\textbf {K}}_1$ and ${\textbf {K}}_2$. The rotation of the feature in the ith image is $\alpha _i \in [0, 2\pi )$ and the size is $q_i \in \mathbb {R}$. The scaling from the 1st to the 2nd image is calculated as $q = q_2 / q_1$ and the rotation as $\alpha = \alpha _2 - \alpha _1$.

In [2], a two-step procedure is proposed for estimating the epipolar geometry. First, a homography is obtained from three oriented features. Finally, the fundamental matrix is retrieved from the homography and two additional correspondences. Even though this technique considers the scales and shear as unknowns, thus estimating the epipolar geometry instead of approximating it, the proposed decomposition of the affine matrix is not justified theoretically. Therefore, the geometric interpretation of the feature rotations is not provably valid. Barath et al. [8] proposes a way of recovering affine correspondences from the feature rotation, scale, and the fundamental matrix. In [10], a method is proposed to estimate the homography from two SIFT correspondences and a theoretically justifiable affine decomposition and general constraints on the homography are provided. Even though having a number of methods estimating geometric entities from SIFT features, there are no solvers that directly exploit the feature orientations and scales for estimating the epipolar geometry in the general case. The reason is that the constraints derived in [10] does not allow directly solving for the pose since each new correspondence yields two equations and, also, two additional unknowns – no constraint is gained on epipolar geometry from considering the orientation and scale.

The contributions of the paper are: (i) We introduce new constraints relating the oriented circles centered on the observed point locations. These constraints relate the SIFT orientations and scales in two images with the elements of affine correspondence $\textbf{A}$. As such, we show that constraints relating $\textbf{A}$ and the parameters of a SIFT correspondence derived in [10] do not describe the full geometric relationship and, therefore, are not sufficient for estimating the epipolar geometry. (ii) Exploiting the new constraints that relate $\textbf{A}$ and the SIFT correspondence, we derive the geometric relationship between orientation and scale-covariant features and epipolar geometry. The new SIFT-based constraint is a linear equation that can be straightforwardly used together with the well-known epipolar constraint to efficiently solve relative pose problems. (iii) Finally, we exploit the new constraint in minimal solvers for estimating epipolar geometry of uncalibrated, calibrated and partially-calibrated cameras with unknown focal length. The new solvers require four SIFT correspondences for estimating the fundamental matrix and three for finding the essential matrix both in the fully and in the partially calibrated cases. The reduced sample size accelerates randomized robust estimation by a large margin on a number of real-world datasets while often leading to better accuracy. Example image pairs are shown in Fig. 1.

2 Theoretical Background

Affine correspondence $(\textbf{p}_1, \textbf{p}_2, \textbf{A})$ is a triplet, where $\textbf{p}_1 = [u_1 \; v_1 \; 1]^\text {T}$ and $\textbf{p}_2 = [u_2 \; v_2 \; 1]^\text {T}$ are a corresponding homogeneous point pair in two images and $\textbf{A}$ is a $2 \times 2$ linear transformation which is called local affine transformation. Its elements in a row-major order are: $a_1$, $a_2$, $a_3$, and $a_4$. To define $\textbf{A}$, we use the definition provided in [28] as it is given as the first-order Taylor-approximation of the $\text {3D} \rightarrow \text {2D}$ projection functions. For perspective cameras, the formula for $\textbf{A}$ is the first-order approximation of the related homography matrix as:

$$\begin{aligned} \begin{array}{lllllll} a_{1} &{} = &{} \frac{\partial {\textbf {u}}_2}{\partial u_1} = \frac{h_{1} - h_{7} u_2}{s}, &{} &{} a_{2} &{} = &{} \frac{\partial {\textbf {u}}_2}{\partial v_1} = \frac{h_{2} - h_{8} u_2}{s}, \\[2mm] a_{3} &{} = &{} \frac{\partial {\textbf {v}}_2}{\partial u_1} = \frac{h_{4} - h_{7} v_2}{s}, &{} &{} a_{4} &{} = &{} \frac{\partial {\textbf {v}}_2}{\partial v_1} = \frac{h_{5} - h_{8} v_2}{s}, \end{array} \end{aligned}$$

(1)

where ${\textbf {u}}_i$ and ${\textbf {v}}_i$ are coordinate functions given the projection function in the ith image ($i \in \{1,2\}$) and $s = u_1 h_7 + v_1 h_8 + h_9$ is the projective depth. The elements of homography $\textbf{H}$ in a row-major order are written as $h_1$, $h_2$, ..., $h_9$.

The relationship of an affine correspondence and a homography is described by six linear equations [4]. First, since an affine correspondence contains a point pair, the well-known equations (from $\alpha \textbf{H}\textbf{p}_1 = \textbf{p}_2$, $\alpha \in \mathbb {R}$) relating the point coordinates hold [18]. The resulting two linearly independent equations are written as follows:

$$\begin{aligned} \begin{array}{ll} u_1 h_1 + v_1 h_2 + h_3 - u_1 u_2 h_7 - v_1 u_2 h_8 - u_2 h_9 &{}= 0, \\ u_1 h_4 + v_1 h_5 + h_6 - u_1 v_2 h_7 - v_1 v_2 h_8 - v_2 h_9 &{}= 0. \end{array} \end{aligned}$$

(2)

Second, after re-arranging Eq. (1), 4 linear constraints are obtained from $\textbf{A}$ as

$$\begin{aligned} \begin{aligned} h_{1} - \left( u_2 + a_{1} u_1 \right) h_{7} - a_{1} v_1 h_{8} - a_{1} h_{9}&= 0,&h_{2} - \left( u_2 + a_{2} v_1 \right) h_{8} - a_{2} u_1 h_{7} - a_{2} h_{9}&= 0, \\ h_{4} - \left( v_2 + a_{3} u_1 \right) h_{7} - a_{3} v_1 h_{8} - a_{3} h_{9}&= 0,&h_{5} - \left( v_2 + a_{4} v_1 \right) h_{8} - a_{4} u_1 h_{7} - a_{4} h_{9}&= 0. \end{aligned} \end{aligned}$$

Consequently, an affine correspondence provides six linear equations in total, for the elements of the related homography matrix.

Fundamental matrix $\textbf{F}$ relating two images of a rigid scene is a $3 \times 3$ projective transformation ensuring the so-called epipolar constraint

$$\begin{aligned} \textbf{p}_2^\text {T}\textbf{F} \textbf{p}_1 = 0. \end{aligned}$$

(3)

Since its scale is arbitrary and $\det (\textbf{F}) = 0$, matrix $\textbf{F}$ has 7 degrees-of-freedom (DoF).

The relationship of the epipolar geometry (either a fundamental or essential matrix) and affine correspondences are described in [6] through the effect of $\mathbf {{A}}$ on the corresponding epipolar lines. Suppose that fundamental matrix $\textbf{F}$, point pair $\textbf{p}$, $\textbf{p}'$, and the related affinity $\textbf{A}$ are given. It can be proven that $\textbf{A}$ transforms $\textbf{v}$ to $\textbf{v}'$, where $\textbf{v}$ and $\textbf{v}'$ are the directions of the epipolar lines ($\textbf{v}, \textbf{v}' \in \mathbb {R}^2$ s.t. $\left\Vert \textbf{v}\right\Vert _2 = \left\Vert \textbf{v}'\right\Vert _2 = 1$) in the first and second images [14], respectively. It can be seen that transforming the infinitesimally close vicinity of $\textbf{p}$ to that of $\textbf{p}'$, $\textbf{A}$ has to map the lines going through the points. Therefore, constraint $\textbf{A} \textbf{v} \parallel \textbf{v}'$ holds.

As it is well-known [40], formula $\textbf{A} \textbf{v} \parallel \textbf{v}'$ can be reformulated as follows:

$$\begin{aligned} \textbf{A}^{-\text {T}} \textbf{n} = \beta \textbf{n}', \end{aligned}$$

(4)

where $\textbf{n}$ and $\textbf{n}'$ are the normals of the epipolar lines ($\textbf{n}, \textbf{n}' \in \mathbb {R}^2$ s.t. $\textbf{n} \bot \textbf{v}$, $\mathbf {n'} \bot \mathbf {v'}$). Scalar $\beta$ denotes the scale between the transformed and the original vectors if $\left\Vert \textbf{n}\right\Vert _2 = \left\Vert \textbf{n}'\right\Vert _2 = 1$. The normals are calculated as the first two coordinates of epipolar lines

$$\begin{aligned} \textbf{l} = \textbf{F}^\text {T}\textbf{p}' = \left[ a \; b \; c \right] ^\text {T}, \quad \textbf{l}' = \textbf{F} \textbf{p} = \left[ a' \; b' \; c' \right] ^\text {T}. \end{aligned}$$

(5)

Since the common scale of normals $\textbf{n} = \textbf{l}_{[1:2]} = \left[ a \; b \right] ^\text {T}$ and $\textbf{n}' = \textbf{l}_{[1:2]}' = \left[ a' \; b' \right] ^\text {T}$ comes from the fundamental matrix, Eq. (4) is modified as follows:

$$\begin{aligned} \textbf{A}^{-\text {T}} \textbf{n} = -\textbf{n}'. \end{aligned}$$

(6)

Formulas (5) and (6) yield two equations which are linear in the parameters of the fundamental matrix as:

$$\begin{aligned} \begin{array}{r} (u' + a_1 u) f_1 + a_1 v f_2 + a_1 f_3 + (v' + a_3 u) f_4 + a_3 v f_5 + a_3 f_6 + f_7 = 0, \end{array}\end{aligned}$$

(7)

$$\begin{aligned} \begin{array}{r} a_2 u f_1 + (u' + a_2 v) f_2 + a_2 f_3 + a_4 u f_4 + (v' + a_4 v) f_5 + a_4 f_6 + f_8 = 0. \end{array} \end{aligned}$$

(8)

Points ($u_1$, $v_1$) and ($u_2$, $v_2$) are the points in the first and second image, respectively.

In summary, the linear part of a local affine transformation gives two linear equations, Eqs. (7) and (8), for epipolar geometry estimation. A point correspondence yields a third one, Eq. (3), through the epipolar constraint. Thus, an affine correspondence yields three linear constraints. As the fundamental matrix has seven DoF, three affine correspondences are enough for estimating $\textbf{F}$ [12].¹ Essential matrix $\textbf{E}$ has five DoF and, thus, two affine correspondences are enough for the estimation [9].

3 Epipolar Geometry and SIFT Features

In this section, we show the relationship of epipolar geometry and orientation and scale-covariant features. Even though we will use SIFT as an alias for this kind of features, the derived formulas hold for all of them. First, the affine transformation model is described in order to interpret the SIFT angles and scales. This model is substituted into the relationship of affine transformations and epipolar geometry. Combining the derived constraint using elimination ideals [20], we finally propose a linear equation characterizing the epipolar consistency of the orientation and scale part of the SIFT features.

3.1 Interpretation of SIFT Features

Reflecting the fact that we are given a scale $q_i \in \mathbb {R}^+$ and rotation $\alpha _i \in [0, 2 \pi )$ independently in each image ($i \in \{ 1, 2 \}$; see Fig. 2b), the objective is to define affine correspondence $\textbf{A}$ as a function of them. Such an interpretation was proposed in [10]. In this section, we simplify the formulas in [10] in order to reduce the number of unknowns in the system. To understand the orientation and scale part of SIFT features, we exploit the definition of affine correspondences proposed by Barath et al. [11]. In [11], $\textbf{A}$ is defined as the multiplication of the Jacobians of the projection functions w.r.t. the image directions in the two images as follows:

$$\begin{aligned} {\textbf {A}} = \textbf{J}_2 \textbf{J}_1^{-1}, \end{aligned}$$

(9)

where $\textbf{J}_1$ and $\textbf{J}_2$ are the Jacobians of the 3D $\rightarrow$ 2D projection functions. Proof is in [10]. For the ith Jacobian, we use the following decomposition:

$$\begin{aligned} \small {\textbf {J}}_i = {\textbf {R}}_i {\textbf {U}}_i = \begin{bmatrix} \cos (\alpha _i) &{} -\sin (\alpha _i) \\ \sin (\alpha _i) &{} \cos (\alpha _i) \end{bmatrix} \begin{bmatrix} q_{u,i} &{} w_i \\ 0 &{} q_{v,i} \end{bmatrix}, \end{aligned}$$

(10)

where angle $\alpha _i$ is the rotation in the ith image, $q_{u,i}$ and $q_{v,i}$ are the scales along axes u and v, and $w_i$ is the shear. Plugging Eq. (10) into Eq. (9) leads to ${\textbf {A}} = {\textbf {R}}_2 {\textbf {U}}_2 ({\textbf {R}}_1 {\textbf {U}}_1)^{-1} = {\textbf {R}}_2 {\textbf {U}}_2 {\textbf {U}}_1^{-1} {\textbf {R}}_1^{\text {T}}$, where ${\textbf {U}}_1$ and ${\textbf {U}}_2$ contain the unknown scales and shears in the two images. Since we are not interested in finding them separately, we replace ${\textbf {U}}_2 {\textbf {U}}_1^{-1}$ by upper-triangular matrix $\mathbf {{U}} = {\textbf {U}}_2 {\textbf {U}}_1^{-1}$ simplifying the formula to

$$\begin{aligned} {\textbf {A}} = {\textbf {R}}_2 \mathbf {{U}} {\textbf {R}}_1^{\text {T}} = \begin{bmatrix} \cos (\alpha _2) &{} -\sin (\alpha _2) \\ \sin (\alpha _2) &{} \cos (\alpha _2) \end{bmatrix} \begin{bmatrix} q_{u} &{} w \\ 0 &{} q_{v} \end{bmatrix} \begin{bmatrix} \cos (\alpha _1) &{} \sin (\alpha _1) \\ -\sin (\alpha _1) &{} \cos (\alpha _1) \end{bmatrix}. \end{aligned}$$

Angles $\alpha _1$ and $\alpha _2$ are known from the SIFT features. Let us use the notation $c_i = \cos (\alpha _i)$ and $s_i = \sin (\alpha _i)$. The equations after the matrix multiplication become

$$\begin{aligned} \small {\textbf {A}} = \begin{bmatrix} a_1 &{} a_2 \\ a_3 &{} a_4 \end{bmatrix} = \begin{bmatrix} c_2 (c_1 q_{u} - s_1 w) + s_2 s_1 q_v &{} c_2 (s_1 q_u + c_1 w) - s_2 c_1 q_{v} \\ s_2 (c_1 q_{u} - s_1 w) - c_2 s_1 q_v &{} s_2 (s_1 q_u + c_1 w) + c_2 c_1 q_{v} \end{bmatrix}. \end{aligned}$$

After simplifying the equations, we get the following linear system

$$\begin{aligned} \begin{array}{lrclr} a_1 &{} = c_2 c_1 q_{u} - c_2 s_1 w + s_2 s_1 q_v, &{} \quad &{} a_2 &{} = c_2 s_1 q_u + c_2 c_1 w - s_2 c_1 q_{v},\\ a_3 &{} = s_2 c_1 q_{u} - s_2 s_1 w - c_2 s_1 q_v, &{} \quad &{} a_4 &{} = s_2 s_1 q_u + s_2 c_1 w + c_2 c_1 q_{v}, \end{array} \end{aligned}$$

(11)

where the unknowns are the affine parameters $a_1$, $a_2$, $a_3$, $a_4$, scales $q_u$, $q_v$ and shear w.

In addition to the previously described constraints, we are given two additional ones. First, it can be seen that the uniform scales of the SIFT features are proportional to the area of the underlying image region and, therefore, the scale change provides constraint

$$\begin{aligned} \small \det {\textbf {A}} = \det \left( {\textbf {R}}_2 \mathbf {{U}} {\textbf {R}}_1^{\text {T}} \right) = \det \mathbf {{U}} = q_u q_v = \frac{q_2^2}{q_1^2}, \end{aligned}$$

(12)

where $q_1$ and $q_2$ are the SIFT scales in the two images. Second, the SIFT orientations and scales in the two images provide an additional constraint as

$$\begin{aligned} \small q_1 {\textbf {A}} \begin{bmatrix} \cos (\alpha _1) \\ \sin (\alpha _1) \end{bmatrix} = q_2 \begin{bmatrix} \cos (\alpha _2) \\ \sin (\alpha _2) \end{bmatrix} \end{aligned}$$

(13)

relating the oriented circles centered on the point correspondence. Next, we show how these constraints can be used to derive the constraint relating the SIFT orientation and scale with the epipolar geometry.

3.2 SIFT Epipolar Constraint

Our goal is to derive constraints that relate epipolar geometry and orientation- and scale-covariant features. To do this, we consider the constraints that relate the elements of $\textbf{A}$ and the measured orientations $\alpha _i$ and scales $q_i$ of the features in the images. In [10], such constraints were derived by eliminating $q_u$, $q_v$ and w from the ideal generated by (11), (12) and trigonometric identities $c_i^2 + s_i^2 = 1$ for $i \in \{1,2\}$, using the elimination ideal technique [20]. This method resulted into two constraints, i.e., the generators of the elimination ideal, one of which is directly (12) and the second one is of form

$$\begin{aligned} \small c_1 s_2 a_1 + s_1 s_2 a_2 - c_1 c_2 a_3 - c_2 s_1 a_4 = 0. \end{aligned}$$

(14)

Here, we will show that once the constraints (13) are added to the ideal, and we ensure $q_1 \ne 0$ and $q_2 \ne 0$ by saturating the ideal with $q_1$ and $q_2$, then the elimination ideal is generated directly by constraints (12) and (13). This means that for the derivation of the constraints that relate the elements of matrix $\textbf{A}$ and the measured orientations $\alpha _i$ and scales $q_i$, equations (11) are not necessary. These new constraints are as follows:

$$\begin{aligned} \small a_2 a_3 - a_1 a_4 + q^2= & {} 0,\end{aligned}$$

(15)

$$\begin{aligned} a_3 c_1+a_4 s_1 - s_2 q= & {} 0, \end{aligned}$$

(16)

$$\begin{aligned} a_1 c_1+a_2 s_1 - c_2 q= & {} 0, \end{aligned}$$

(17)

where $q= \frac{q_2}{q_1}$. Moreover, thanks to constraints (13) relating the oriented circles centered on the points, which were not used in [10], we have three constraints, compared to the two polynomials derived in [10]². This will help us to derive a new constraint relating epipolar geometry and covariant features that was not possible to derive using only the two constraints proposed in [10]. For this purpose, we create an ideal J generated by polynomials (15)–(17), (7) and (8). Then the unknown elements of the affine transformation $\textbf{A}$ are eliminated from the generators of J. We do this by computing the generators of the elimination ideal $J_1 = J \cap \mathbb {C}[f_1,\dots ,f_9,u_1,v_1,u_2,v_2,q,s_1,c_1,s_2,c_2]$. The elimination ideal $J_1$ is generated by the polynomial

$$\begin{aligned} c_2qf_1u_1+s_2qf_4u_1+c_2qf_2v_1+s_2qf_5v_1+c_2qf_3+s_2qf_6+\\ \nonumber c_1f_1u_2+s_1f_2u_2+c_1f_4v_2+s_1f_5v_2+c_1f_7+s_1f_8= 0. \end{aligned}$$

(18)

Note that (18) is linear in the elements of $\textbf{F}$ and, as such, it can be straightforwardly used together with the well-known epipolar constraint for point correspondences to estimate the epipolar geometry.

3.3 Solvers for Epipolar Geometry

In this section, we will describe different solvers for estimating epipolar geometry using orientation- and scale-covariant features (e.g., SIFT correspondences). In Sect. 3.2, we showed that each SIFT correspondence gives us two linear constraints on the elements of the fundamental (or essential) matrix. One constraint is the well-known epipolar constraint (3) for point correspondences and one is the new derived SIFT-based constraint (18). As such, we can directly transform all existing point-based solvers for estimating epipolar geometry to solvers working with SIFT features. The only difference will be that for solvers that estimate the geometry from n point correspondences, we will use $\lceil \frac{n}{2} \rceil$ SIFT ones, and in the solver we will replace $\lfloor \frac{n}{2} \rfloor$ epipolar constraints (3) from point correspondences with $\lfloor \frac{n}{2} \rfloor$ SIFT constraints of the form (18). This will affect only some coefficients in coefficient matrices used in these solvers and not the structure of the solver. Moreover, for problems where n, which in this case corresponds to the DoF of the problem, is not a multiple of two, we can use all $\lceil \frac{n}{2} \rceil$ available constraints of the form (18) to simplify the solver. Next, we will describe solutions to three important relative pose problems, i.e. for uncalibrated, calibrated, and partially calibrated perspective cameras with unknown focal length. However, note, that our method is not only applicable to these problems and presented solvers, but can be directly applied to all existing point-based solvers for estimating epipolar geometry.

Fundamental Matrix. This is a 7 DoF problem, which means that we need four SIFT correspondences $(\textbf{p}_1^i, \textbf{p}_2^i,\alpha _1^i,\alpha _2^i,q)$, $i \in \{1,2,3,4\}$ to solve it. For the ith correspondence, the epipolar constraint (3) and the proposed SIFT-based constraint (18) can be written as $\textbf{C}_i \textbf{f} = 0$, where matrix $\textbf{C}_i \in \mathbb {R}^{2\times 9}$ is the coefficient matrix consisting of two rows and vector $\textbf{f} = [ f_1, f_2, f_3, f_4, f_5, f_6, f_7, f_8, f_9 ]^\text {T}$ consists of the unknown elements of the fundamental matrix. As mentioned above, in this case, we can either use all four constraints of the form (18) and simplify the solver by not using the $\det \mathbf {{F}} = 0$ constraint³, or we can use just three equations of the form (18) and solve the obtained cubic polynomial implied by the constraint $\det \mathbf {{F}} = 0$. In our experiments, we decided to test the second solver, which corresponds to the well-known seven-point solver [18] and which leads to more accurate results.

Essential Matrix. The relative pose problem for calibrated cameras is a 5 DoF problem and we need three SIFT correspondences $(\textbf{p}_1^i, \textbf{p}_2^i,\alpha _1^i,\alpha _2^i,q)$, $i \in \{1,2,3\}$ to solve it. Similarly to the uncalibrated case, for the ith correspondence, the epipolar constraint and the new SIFT-based one can be written as $\textbf{C}_i \textbf{e} = 0$, where $\textbf{e} = [ e_1, \dots , e_9 ]^\text {T}$ is the vector of the unknown elements of the essential matrix. Matrix $\textbf{C}_i \in \mathbb {R}^{2\times 9}$ is the coefficient matrix consisting of two rows, the first one containing coefficients from the epipolar constraint and the second one from the SIFT-based one (18). Considering the three feature case, $\textbf{C}$ is of size $6 \times 9$ as $\textbf{C} = [ \textbf{C}_1^\text {T}, \textbf{C}_2^\text {T}, \textbf{C}_3^\text {T}]^\text {T}$. While using the top $5 \times 9$ sub-matrix of $\textbf{C}$ would allow using the well-known solvers for solving the five-point problem [17, 21, 30], having 6 rows in $\textbf{C}$ allows to use simpler solvers. We, thus, adopt the solver from [9] proposed, originally, for estimating from affine correspondences.

First, the 3-dimensional null-space of $\textbf{C}$ is obtained by, e.g., LU decomposition as it is significantly faster than the SVD and Eigen decompositions. The solution is given by a linear combination of the three null-space basis vectors $\textbf{n}_1$, $\textbf{n}_2$, and $\textbf{n}_3$ as $\textbf{e} = \alpha \textbf{n}_1 + \beta \textbf{n}_2 + \gamma \textbf{n}_3$, where parameters $\alpha$, $\beta$, and $\gamma$ are unknown non-zero scalars. These scalars are defined up to a common scale, therefore, one of them can be set to an arbitrary value. In the proposed algorithm, $\gamma = 1$.

By substituting this expression for $\textbf{e}$ to the determinant constraint $\det \textbf{E} = 0$ and the trace constraint, i.e., $\textbf{E} \textbf{E}^\text {T}\textbf{E} - \frac{1}{2} \text {trace}(\textbf{E} \textbf{E}^\text {T}) \textbf{E} = 0$, ten polynomial equations in two unknowns $\alpha$ and $\beta$ are obtained. They can be formed as $\textbf{Q} \textbf{y} = \textbf{b}$, where $\textbf{Q}$ and $\textbf{b}$ are the coefficient matrix and the inhomogeneous part (i.e., coefficients of monomial 1), respectively. Vector $\textbf{y} = [ \alpha ^3 , \beta ^3 , \alpha ^2 \beta , \alpha \beta ^2 , \alpha ^2 , \beta ^2 , \alpha \beta , \alpha , \beta ]^\text {T}$ consists of nine monomials of the system and $\textbf{Q}$ is a $10 \times 9$ coefficient matrix. Not considering dependencies of monomials in $\textbf{y}$, we can consider this an over-determined system of ten linear equations in nine unknowns. Its optimal solution in least squares sense is given by $\textbf{y} = \textbf{Q}^{\dag } \textbf{b}$, where matrix $\textbf{Q}^{\dag }$ is the Moore-Penrose pseudo-inverse of matrix $\textbf{Q}$. The solver has only a single solution which is beneficial for the robust estimation.

The elements of the solution vector $\textbf{y}$ are dependent. Thus $\alpha$ and $\beta$ can be obtained in multiple ways, e.g., as $\alpha _1 = y_8$, $\beta _1 = y_9$ or $\alpha _2 = \root 3 \of {y_1}$, $\beta _2 = \root 3 \of {y_2}$. To choose the best candidates, we paired every possible $\alpha$ and $\beta$ and selected the one minimizing the trace constraint $\textbf{E} \textbf{E}^\text {T}\textbf{E} - \frac{1}{2} \text {trace}(\textbf{E} \textbf{E}^\text {T}) \textbf{E} = 0$.

Fundamental Matrix and Focal Length. Assuming the unknown common focal length in both cameras, the relative pose problem has 6 DoF. As such, it can be solved from three SIFT correspondences $(\textbf{p}_1^i, \textbf{p}_2^i,\alpha _1^i,\alpha _2^i,q)$, $i \in \{1,2,3\}$. In this case, three SIFT correspondences generate exactly the minimal case. We can apply one of the standard 6PT solvers [17, 20, 22, 37]. We choose the method from [20] that uses elimination ideals to eliminate the unknown focal length and generates a smaller elimination template matrix than the original Gröbner basis solver [37].

4 Experiments

In this section, we test the proposed SIFT-based solvers in a fully controlled synthetic environment and on a number of publicly available real-world datasets.

Fig. 3.

Synthetic experiments. (a) The frequencies (100 000 runs; vertical axis) of $\text {log}_{10}$ sym. epipolar errors (horizontal; in pixels) in the essential and fundamental matrices estimated by point and SIFT-based solvers. (b) The frequencies of $\text {log}_{10}$ relative focal length errors (horizontal) estimated by point and SIFT-based solvers. (c) The symmetric epipolar error plotted as a function of the image noise in pixels.

4.1 Synthetic Experiments

To test the accuracy of the relative pose obtained by exploiting the proposed SIFT constraint, first, we created a synthetic scene consisting of two cameras represented by their $3 \times 4$ projection matrices $\textbf{P}_1$ and $\textbf{P}_2$. They were located randomly on a center-aligned sphere with its radius selected uniformly randomly from range [0.1, 10]. Two planes with random normals were generated at most one unit far from the origin. For each plane, ten random points, lying on the plane, were projected into both cameras. Note that we need the correspondences to originate from at least two planes in order to avoid having a degenerate situation for fundamental matrix estimation. To get the ground truth affine transformation for a correspondence originating from the jth plane, $j \in \{1, 2\}$, we calculated homography $\textbf{H}_j$ by projecting four random points from the plane to the cameras and applying the normalized DLT [18] algorithm. The local affine transformation of each correspondence was computed from the ground truth homography by (1). Note that $\textbf{H}$ could have been calculated directly from the plane parameters. However, using four points promised an indirect but geometrically interpretable way of noising the affine parameters: adding noise to the coordinates of the four points initializing $\textbf{H}$. To simulate the SIFT orientations and scales, $\textbf{A}$ was decomposed to $\textbf{J}_1$, $\textbf{J}_2$. Since the decomposition is ambiguous, $\alpha _1$, $q_{u,1}$, $q_{v,1}$, $w_1$ were set to random values. $\textbf{J}_1$ was calculated from them. Finally, $\textbf{J}_2$ was calculated as $\textbf{J}_2 = \textbf{A}\textbf{J}_1$. Zero-mean Gaussian-noise was added to the point coordinates, and, also, to the coordinates which were used to estimate the affine transformations.

Figure 3a reports the numerical stability of the methods in the noise-free case. The frequencies (vertical axis), i.e., the number of occurrences in 100 000 runs, are plotted as the function of the $\log _{10}$ average symmetric epipolar error (in pixels; horizontal) computed from the estimated model and the unused correspondences. All methods on all problems lead to stable solutions. While the 3SIFT essential matrix solver seems the least stable, it is important to note that the horizontal axis is in pixels and, therefore, having ${\approx }10^{-5}$ pixel maximum error can be considered stable. Figure 3b reports the numerical stability of the estimated focal lengths in the semi-calibrated case. The horizontal axis is the $\log _{10}$ relative focal length error calculated as $\epsilon _f = |f_{\text {est}} - f_{\text {gt}}| / f_{\text {gt}}$. Both methods lead to stable solutions.

In Fig. 3c, the average symmetric epipolar (over 10 000 runs; in pixels) errors are plotted as the function of the image noise added both to the point coordinates and affine parameters (indirectly, via contaminating the initializing homography). The error is calculated on correspondences not used for the estimation. The SIFT-based solvers are slightly more sensitive to the noise than the point-based one. This is expected since the image noise has a larger impact on the affine parameters, due to their localized nature, than on the point coordinates [12]. Interestingly, this is not the case when solving the semi-calibrated case, where the SIFT-based solver leads to the most accurate relative poses. Still, the main message from Fig. 3c is that the solvers behave reasonably well against increasing image noise. In the next section, we will show that, due to the reduced combinatorics of the problem, the SIFT-based methods often yield more accurate solutions than their point-based counterparts inside RANSAC.

4.2 Real-World Experiments

Table 1. Average rotation, translation (in degrees) and focal length errors, run-times (in milliseconds), and iteration numbers on the KITTI [15] and PhotoTourism [3] datasets for essential (E) and fundamental (F) matrix estimation and, also, focal length plus fundamental matrix estimation (F + f). On the PhotoTourism dataset, we show the median errors.

Fig. 4.

The cumulative distribution functions of the rotation and translation errors ($^\circ$) and run-times (secs) of epipolar geometry estimation by GC-RANSAC [5] combined with point-based and the proposed SIFT-based minimal solvers on 69 537 image pairs from the KITTI dataset [15]. The frame difference is denoted by color, e.g., pairs ($I_i$, $I_{i+2}$) are considered for the green curve.

For testing the methods, we use the KITTI benchmark [15] and the datasets from CVPR tutorial RANSAC in 2020 [3]. Considering that the orientation and scale of local features are noisier than their point coordinates, we chose to use a locally optimized RANSAC, i.e., GC-RANSAC [5], as the robust estimator, where the local optimization is applied to only the point coordinates, similarly as in [10, 12]. The required confidence is set to 0.99 and the maximum iteration number to 5000.

In GC-RANSAC (and other RANSAC-like methods), two different solvers are used: (a) one for fitting to a minimal sample and (b) one for fitting to a non-minimal sample when doing model polishing on all inliers or in the local optimization step. For (a), the main objective is to solve the problem using as few points as possible since the run-time depends exponentially on the number of points required for the model estimation. The proposed and compared solvers were included in this part of the robust estimator.

The KITTI odometry benchmark consists of 22 stereo sequences. Only 11 sequences (00–10) are provided with ground truth trajectories for training. We use these 11 sequences to evaluate the compared solvers. Each image is of resolution $1241 \times 376$. We ran the methods on image pairs formed such that the frame distance is 1, 2 or 4. For example, frame distance 2 means that we form pairs from images $I_i$ and $I_{i+2}$, where $i \in [1, n]$ and $n \in \mathbb {N}^+$ is the number of images in a sequence. In total, the algorithms were tested on 69 537 pairs. To form tentative correspondences, we detected 8000 SIFT keypoints in both images to have a reasonably dense point cloud reconstruction and precise camera poses [39]. We combined mutual nearest neighbor check with standard distance ratio test [23] to establish tentative correspondences, as recommended in [39].

The RANSAC tutorial dataset comes from the train and validation sets of the CVPR IMW 2020 PhotoTourism challenge. We use the two scenes, each consisting of 4950 image pairs, provided for validation purposes to test the proposed SIFT-based and the traditional point-based solvers.

4.3 Essential Matrix Estimation

For essential matrix estimation, we compare the 5PT algorithm (implemented in the Theia library [38]) to the SIFT-based solver described in Sect. 3.3. The solver used for fitting to a larger-than-minimal sample in GC-RANSAC is the 5PT algorithm. The inlier-outlier threshold is set to 0.75 pixels and is normalized by the focal lengths.

The cumulative distribution functions (CDF) of the rotation and translation errors (in degrees) and run-times (in seconds) of $\textbf{E}$ estimation on the 69 537 image pairs from the KITTI dataset are in Fig. 4a. The frame difference is denoted by color, e.g., image pairs ($I_i$, $I_{i+2}$) are considered for the green curve. The proposed solver yields almost exactly the same accuracy as the widely used point-based one while being significantly faster as shown in the right plot. For example, when the frame distance is 4, GC-RANSAC with the point-based solver finishes earlier than 0.1 s only on the ${\approx }17\%$ of the images pairs. GC-RANSAC with the SIFT-based solver finishes faster than 0.1 s in the $98\%$ of the cases. The results on the PhotoTourism dataset look similar in Fig. 5a. In this case, the proposed solver leads to comparable results to the 5PT algorithm and it is, again, significantly faster.

The corresponding avg. errors, run-times and iteration numbers are reported in the first two rows of Table 1. On KITTI, all methods have similar accuracy with the SIFT-based ones being five times faster and real-time. On the PhotoTourism dataset, we show the median errors since it is significantly more challenging than KITTI and, thus, all methods fail on some pairs. Both the rotation and translation errors are similar for all solvers. The run-time of the 3SIFT solver is eight times lower than that of 5PT.

4.4 Fundamental Matrix Estimation

For $\textbf{F}$ estimation, we compare the 7PT algorithm [18] to the SIFT-based solver described in Sect. 3.3. The solver used for fitting to a larger-than-minimal sample in GC-RANSAC is the normalized 8PT algorithm. The inlier threshold is set to 0.75 px.

The CDFs of the rotation and translation errors (in degrees) and run-times (in seconds) of $\textbf{F}$ estimation on the 69 537 image pairs from KITTI are in Fig. 4b. Similarly as in the $\textbf{E}$ estimation figure, the proposed solver yields almost exactly the same accuracy as the widely used point-based one while being significantly faster as shown in the right plot. The run-time difference is marginally smaller in this case due to the 7PT solver, used for $\textbf{F}$ fitting, having fewer solutions than the 5PT algorithm. The results on the PhotoTourism dataset in Fig. 5b show that the proposed solver leads to the most accurate results while being three times faster than its point-based counterpart.

The corresponding average errors, run-times and iteration numbers are reported in the second two rows of Table 1. On KITTI, all methods have similar accuracy while the SIFT-based solver is almost three times faster than the point-based one. On the PhotoTourism dataset, the SIFT-based solver leads to results superior to the point-based one both in terms of relative pose accuracy and run-time. Additional experiments are in the supplementary material.

4.5 Fundamental Matrix and Focal Length Estimation

For $\textbf{F}$ with focal length estimation, we compare the 6PT algorithm of [20] to the SIFT-based solver described in Sect. 3.3. The inlier-outlier threshold is set to 0.75 pixels. The CDFs of the rotation and translation errors (in degrees) and run-times (in seconds) on the 69 537 image pairs from the KITTI dataset are in Fig. 4c. Similarly as in the previous experiments, the proposed solver leads to almost exactly the same accuracy as the widely used point-based one while being significantly faster as shown in the right plot. The results on the PhotoTourism dataset in Fig. 5c show that the proposed solver leads to increased accuracy compared to the 6PT solver while, also, being notably faster. Note that, in order to use this solver, we used only those image pairs from the PhotoTourism dataset where the focal lengths are similar.

The corresponding average errors, run-times and iteration numbers are reported in the last two rows of Table 1. The proposed solvers lead to the most accurate results while being the fastest by a large margin on both datasets.

Fig. 5.

The cumulative distribution functions of the rotation and translation errors ($^\circ$) and run-times (secs) of epipolar geometry estimation by GC-RANSAC [5] combined with point-based and the proposed SIFT-based minimal solvers on 9900 image pairs from the PhotoTourism dataset [3].

5 Conclusion

We derive the general relationship of the epipolar geometry of perspective cameras and orientation and scale-covariant features. It is characterized by two linear equations, one from the point correspondence and one from the orientations and scales. These constraints can be used within all existing relative pose solvers to halve the number of correspondences required for the estimation. This leads to either similar or better accuracy while significantly accelerating the robust estimation – by 4.3 times, on average, on the tested popular computer vision problems.