Scheduling with Machine Conflicts

Abstract

We study the scheduling problem of makespan minimization with machine conflicts that arise in various settings, e.g., shared resources for pre- and post-processing of tasks or spatial restrictions. In this context, each job has a blocking time before and after its processing time, i.e., three parameters. Given a set of jobs, a set of machines, and a graph representing machine conflicts, the problem SchedulingWithMachineConflicts (smc), asks for a conflict-free schedule of minimum makespan in which the blocking times of no two jobs intersect on conflicting machines.

We show that, unless $\text {P} =\text {NP}$, smc on m machines does not allow for a $\mathcal {O}(m^{1-\varepsilon })$-approximation algorithm for any $\varepsilon >0$, even in the case of identical jobs and every choice of fixed positive parameters, including the unit case. Complementary, we provide approximation algorithms when a suitable collection of independent sets is given. Finally, we present polynomial time algorithms to solve the problem for the case of unit jobs smc-Unit on special graph classes. As our main result, we solve smc-Unit for bipartite graphs by using structural insights for conflict graphs of star forests. As the set of active machines at each point in time induces a bipartite graph, the insights yield a local optimality criterion.

D. Schmidt genannt Waldschmidt—was funded by the DFG under Germany’s Excellence Strategy - The Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689).

1 Introduction

Distributing tasks smartly is a challenge we face in numerous settings, ranging from every day life to optimization of industrial processes. Often these assignments must satisfy additional requirements. In this work, we study a variant of the well-studied scheduling problem of makespan minimization when machine conflicts are present. These conflicts arise in various contexts as a result of shared resources or spatial constraints which prohibit machines to complete certain tasks simultaneously. We are particularly interested in situations when external pre- and post-processing of jobs is necessary immediately before and after jobs are internally processed by a machine.

Conflicts of pre- and post-processing may be due to shared resources or spatial constraints. Examples of shared resources arise in manufacturing and logistics, where a common server is used for loading and unloading jobs onto and from machines immediately before or after jobs can be processed. Specific examples mentioned in the literature include manufacturing systems served by a single robot which can only serve one machine at a time [22, 30] or steel production in which furnaces must be served non-preemptively before and after heating processes [41]. Another example of shared resources appears in computing problems, in which different processors may share different databases or external processors that must be accessed before and after executing tasks on the processor and can only be accessed by one processor at a time. An up-to-date example of spatial conflicts occurs in pandemics when schedulers are faced with potentially infectious jobs which should keep sufficient distance to each other, e.g., in testing or vaccination centers. Similarly, spatial conflicts play a crucial role when jobs may have private information or data that should not be shared; e.g., the interrogation of suspects in multiple rooms.

The Problem. SchedulingWithMachineConflicts (smc) is a scheduling problem in which jobs on conflicting machines are processed such that certain blocking intervals of their processing time do not overlap. An instance of $\textsc {smc}$ is defined by a set of jobs $\mathcal {J}$ and a conflict graph $G=(V,E)$ on a set of machines V where two machines i and $i'$ are in conflict if and only if $\{i,i'\} \in E$. In contrast to classical scheduling problems, each job j has three parameters  , where and denote the first and second blocking time of j, respectively, and $p_j$ denotes its processing time. Together they constitute the system time ; note that the order must be maintained. We seek schedules in which the blocking times of no two jobs on conflicting machines intersect. For an example consider Fig. 3. Formally, a (conflict-free) schedule $\varPi$ is an assignment of jobs to machines and starting times such that

• for each point in time, every machine executes at most one job,

• for every edge $\{i,i'\} \in E$ and two jobs $j,j'\in \mathcal {J}$ assigned to machines i and $i'$, respectively, the intervals of the blocking times of j and $j'$ do not overlap interiorly in time.

Moreover, jobs cannot be interrupted, i.e., the starting and completions times of each job differ by the system time. In other words, all schedules are non-preemptive. The makespan $\Vert \varPi \Vert$ of a schedule $\varPi$ is defined as the earliest point in time when all jobs are completed. We seek for a schedule with minimum makespan. Throughout this paper, we use $n:=|\mathcal {J}|$ and $m:=|V|$ to refer to the number of jobs and machines, respectively.

1.1 Our Contribution and Organization

We first consider the problem smc with identical jobs (smc-Id). Identifying intrinsic connections to maximum independent sets, we show that even if are fixed positive parameters for any $\epsilon > 0$, there is no $\mathcal {O}(m^{1-\varepsilon })$-approximation for smc-Id, unless $\text {P} =\text {NP}$ (Theorem 1). However, when a suitable collection of maximum independent sets is given or can be found in polynomial time, we present approximation algorithms with performance guarantee better than 2.5 (Theorem 2). An approximation algorithm can also be obtained when approximate maximum independent sets are at hand (Theorem 3).

In Sect. 3, we consider smc with unit jobs (smc-Unit), i.e., . Motivated by the inapproximability result for smc-Unit on general graphs (Theorem 1), we focus on special graph classes. As our main result, we present a polynomial time algorithm to compute optimal schedules on bipartite graphs. Bipartite graphs are of special interest, because for any conflict graph and for every point in time, the set of active machines induces a bipartite graph. Hence, our insights can be understood as local optimality criteria of schedules for all graphs. To solve the problem to optimality we develop a divide-and-conquer algorithm based on structural insights for stars. Moreover, we provide an efficient representation of schedules so that the running time of our algorithm is polynomial in the size of G and $\log (n)$.

Full details of all proofs are presented in the appendix (see Sect. 5 and Sect. 6). A full version can be found at [11].

1.2 Related Work

The problem smc generalizes the classical scheduling problem of makespan minimization on parallel identical machines, also denoted by $P||C_{\max }$ in the three-field notation [21]. In fact, $P||C_{\max }$ is equivalent to two special cases of $\textsc {smc}$:

• if the blocking times of all jobs vanish, i.e., for all $j\in \mathcal {J}$, and

• if the edge set of the conflict graph is the empty set.

For a constant number of machines, $P||C_{\max }$ is weakly NP-hard, while it is strongly NP-hard when m is part of the input [18]. Graham [19, 20] introduced list scheduling algorithms to obtain the first constant approximation algorithms for this problem. Improved approximation guarantees have been achieved by a fully polynomial time approximation scheme (FPTAS) when m is constant [38] and a polynomial time approximation scheme (PTAS) when m is part of the input [26]. In subsequent work, the latter has been improved to efficient polynomial time approximation schemes (EPTAS), we refer to [4, 13, 25, 28, 29].

Scheduling with pre- and post-processing has been considered in different models in the literature. One such model was introduced by Hall et al. [22] in which jobs must be scheduled non-preemptively on identical parallel machines but have to be pre-processed by a common server immediately. This model corresponds to smc with for all jobs j and a complete graph as the conflict graph. The special cases of unit first blocking times and $m=2$ [22] and the case of identical processing times $p_j=p\, \forall j$ and $m=2$ [10] were shown to be weakly $\text {NP}$-hard, while the cases of and $m=2$ [22] and the case of  [35] were shown to be strongly $\text {NP}$-hard. On the positive side, if the problem can be solved in time $\mathcal {O}(n)$ [22]. Moreover, Kravchenko and Werner [35] present a pseudo-poynomial algorithm for the case of and $m=2$. Xie et al. [41] extend this model to a single server used for pre- and post-processing. This problem corresponds to smc with $K_m$ as the conflict graph. Xie et al. [41] and Jiang et al. [30] analyze the worst case performance of the list scheduling algorithms introduced by Graham [19, 20]. Furthermore, heuristics and mixed-integer programming techniques were developed for several special cases [1,2,3, 16, 33]. Two other models are the master-and-slave problem introduced by Kern and Nawijn [31] and termed by Sahni [39] and the problem of scheduling jobs with segmented self-suspension introduced by Rajkumar et al. [37]. Chen et al. [12] present an approximation algorithm for the special case of a single suspension interval in which each job consists of three components.

The concept of machine conflicts has previously also been considered in the context of buffer minimization on multiprocessor systems. Chrobak et al. [14] show that there is no polynomial approximation ratio unless $\text {P} =\text {NP}$. For the online case, they present competitive algorithms for general graphs as well as special graph classes. Höhne and van Stee [27] develop competitive algorithms when the conflict graph is a path.

Scheduling with conflict graphs has also been investigated in presence of job conflicts. While in one model, the conflicting jobs cannot be scheduled on the same machine [7, 9, 15], in a second model, the conflicting jobs may not be processed concurrently on different machines [5, 6, 8, 17, 23, 40]. In these works, the complexity and approximability has been investigated for special classes of conflict graphs in both settings.

2 Identical Jobs

In this section, we consider smc with identical jobs, denoted by smc-Id. More specifically, smc-Id $(G,n,($ ,p, $))$ denotes an instance with a conflict graph G and n identical jobs with parameters . We present hardness and approximation results for any fixed choice of . Using the fact that there exists no $O(m^{\varepsilon -1})$-approximation for computing maximum independent sets [24, 36, 42], we obtain an inapproximability result for all fixed positive constants .

Theorem 1

For any $\epsilon > 0$, there exists no $\mathcal {O}(m^{1-\varepsilon })$-approximation for smc-Id, unless $\text {P} =\text {NP}$. This even holds for any fixed positive parameters .

Note that this result holds even for the case when the running time depends polynomially on n (instead of $\log (n)$).

Proof-Sketch

We distinguish the two cases when either all jobs have long blocking times, i.e., (Theorem 5), or all jobs have short blocking times, i.e., (Theorem 8). By symmetry, we may assume that .

For long blocking times, we show that any schedule is basic, i.e., it uses only an independent set of machines (Lemma 8). The inapproximability result follows from the connection to the problem of finding a maximum independent set.

For short blocking times, we use a notion generalizing a maximum independent set. For a graph $G=(V,E)$ and $c\in \mathbb {N}_{\ge 1}$, a maximum induced c-colorable subgraph, or short maximum c-IS, of G is a set of c disjoint independent sets $\mathcal {I} _1,\ldots ,\mathcal {I} _c \subseteq V$ whose union has maximum cardinality. Clearly, a 1-IS is an independent set. Any schedule induces a c-IS and it can be found in polynomial time (Lemma 9). Because the length of a schedule is related to the size of its induced c-IS (Lemma 12), an approximation algorithm yields an approximate maximum c-IS with a performance guarantee of the same order. However, for any $c\in \mathbb {N}_{\ge 1}$, a maximum c-ISs is inapproximable [36].

By the proof of Theorem 1, finding a maximum c-IS polynomially reduces to smc-Id. One may wonder how the difficulty changes, when maximum c-ISs of the graph are at hand. We show that if we are given a suitable collection of maximum independent sets of the conflict graph, we obtain approximation algorithms with performance guarantee better than 2.5. To this end, we define a class of partial schedules using a collection of independent sets of machines.

c-Patterns. Consider an instance of smc-Id on a conflict graph G. Let $c\in \mathbb {N}_{\ge 1}$ with and let $\mathcal {I}=(I_1,I_2,\dots , I_c)$ be a c-tuple of disjoint independent sets of G. A partial schedule of length starting at time t is called a c-pattern on $\mathcal {I}$ if on each machine i in $I_{\ell }$ with $\ell \in \{1,\dots ,c\}$, there is one job starting at time , see also Fig. 1.

Fig. 1.

A 3-pattern on three disjoint independent sets $I_1,I_2,I_3$.

Theorem 2

Let G be a graph and let be the system time. If and we are given a maximum 1-IS of G, then an optimal schedule of smc-Id can be computed in polynomial time.

If and we are given a maximum -IS of G, then smc-Id allows for a -approximation, where . If , it even allows for an $(1+p/q)$-approximation, where $(1+p/q)<2$.

Proof-Sketch

For long blocking times, any schedule is basic and hence, an optimal schedule uses the provided maximum independent set and can thus be computed in polynomial time (Theorem 6).

For short blocking times, we provide a lower bound on the optimal makespan. Specifically, we bound the number of jobs starting within an interval of length $\lambda$ for some specific $\lambda \le q$. We then show that the number of jobs is bounded by $\alpha$, the size of a maximum -IS. This yields a lower bound of $\lambda \cdot \lceil n/\alpha \rceil$ on the optimal makespan. To obtain an upper bound, we construct a schedule which repeatedly uses $(k+1)$-patterns, where .    $\square$

Similarly, if we are given an approximate c-IS of the conflict graph for some suitable c, corresponding approximation results can be derived.

Theorem 3

Let G be a graph. If and we are given a $1/\gamma$-approximate 1-IS of G, then smc-Id allows for a $\lceil \gamma \rceil$-approximation.

If and we are given a $1/\gamma$-approximate -IS of G, then smc-Id allows for a $5\gamma$-approximation.

3 Unit Jobs

Now, we turn our attention to smc-Unit in which we are given n identical unit jobs where for all jobs. On one hand, there exists no $\mathcal {O}(m^{1-\varepsilon })$-approximation for smc-Unit on general graphs with m vertices, unless $\text {P} =\text {NP}$ (Theorem 1). On the other hand, Theorem 2 yields a $4/3$-approximation algorithm for smc-Unit if we are given a maximum 2-IS. Therefore, to improve this performance guarantee, we focus on special graph classes (for which maximum 1- and 2-IS can be computed in polynomial time).

Complete graphs play a special role in the context when machines share a single resource. We show that smc-Unit on complete graphs can be reduced to smc-Unit on a single edge and solved efficiently.

Lemma 1

For every n, an optimal schedule for smc-Unit $(K_m,n)$ can be computed in time linear in $\log n$. In particular, for $m\ge 2$, it coincides with an optimal schedule for $K_2$ of makespan $4\lfloor n/2\rfloor +3(n \mod 2)$.

Bipartite graphs constitute the arguably most interesting graph class in this context because for each schedule, the set of active machines at any point in time induces a bipartite subgraph. Therefore, optimal schedules on bipartite graphs can be understood as a local optimality criterion.

Observation 2

Consider an instance smc-Unit on a graph G and a feasible schedule $\varPi$. For every point in time t, the set of machines processing a job at time t in $\varPi$ induces a bipartite subgraph of G.

Note that a maximum 1-IS of a bipartite graph can be computed in polynomial time [34] and the maximum 2-IS is trivially the entire vertex set. In the remainder, we present a polynomial time algorithm to compute optimal schedules.

Theorem 4

For every bipartite graph G and every n, an optimal schedule for smc-Unit $(G,n)$ can be computed in polynomial time.

Our algorithm is based on a divide-and-conquer technique. In a first step, we derive structural insights of optimal schedules on stars which allow to solve smc-Unit on stars in polynomial time (Sect. 3.1). In a second step, we show how to exploit these insights to find optimal schedules on general bipartite graphs by considering a subgraph whose components are stars with special properties (Sect. 3.2). Finally, we present a polynomial time algorithm to find an adequate subgraph (Sect. 3.3).

3.1 Stars

An essential step towards our polynomial time algorithm for bipartite graphs is to investigate the structure of optimal schedules on stars. A star is a complete bipartite graph $S_{\ell }:=K_{1,\ell }$ on $\ell +1\ge 2$ vertices. For $\ell \ge 2$, $S_{\ell }$ has $\ell$ leaves and a unique center of degree $\ell$. For $\ell =1$, either vertex can be seen as the center of $S_{1}$. We show that optimal schedules on stars can be obtained by using special types of 1- and 2-patterns (see definition of c-pattern for $c=1,2$). We define the special patterns as follows.

A/B-Patterns. An A-pattern on a graph H is a 1-pattern on some maximum 1-IS of H. A B-pattern on H is a 2-pattern on some maximum 2-IS of H. Note that the difference to 1- and 2-patterns is that we do not specify the 1- and 2-ISs. An AB-schedule on H consists of A- and B-patterns only. Consider Fig. 2 for an example. Let $n\in \mathbb N$. We say smc-Unit (H, n) admits an optimal AB-schedule if there exists an optimal schedule that can be transformed into an AB-schedule on H by possibly adding more jobs without increasing the makespan.

Fig. 2.

An AB-schedule on $S_3$ consisting of one A-pattern followed by one B-pattern.

Fig. 3.

Optimal schedule on a tree with 7 machines and 22 jobs with makespan 12.

Using these patterns we derive a structural property of optimal schedules for smc-Unit on stars that allows us to compute them in polynomial time.

Lemma 3

For every star S and every n, smc-Unit (S, n) admits an optimal AB-schedule.

Proof

The statement is obvious for $S_1$. For a star $S_\ell$ with $\ell \ge 2$, consider an optimal schedule and determine a leaf processing a maximum number of jobs. Changing all leaves to this schedule may only increase the number of processed jobs and yields a valid schedule in which all $\ell$ leaves have the same induced schedule. Finally, for each job j processed on a leaf of $S_\ell$, there exist two cases: If no job is processed on the center vertex of the star during the system time (of length 3) of j, we obtain an A-pattern. Otherwise, the job on the center and the job on the leaves are shifted by exactly one time step and we obtain a B-pattern.

   $\square$

Corollary 1

For every star S and every n, an optimal schedule for smc-Unit (S, n) can be computed in time linear in $\log n$ and |S|.

Specifically, for every $S_\ell$, there exists $X\in \{A,B\}$ such that an optimal schedule has at most 2 X-patterns, i.e., an optimal schedule has makespan

$$\begin{aligned} \min _{k=0,1,2} \left\{ 4\bigg \lceil \frac{n-k\ell }{\ell +1}\bigg \rceil +3k, 3\bigg \lceil \frac{n-k(\ell +1)}{\ell }\bigg \rceil +4k \right\} , \end{aligned}$$

(1)

where $\lceil \cdot \rceil$ denotes the usual ceiling function; however, for negative reals it evaluates to 0.

We later exploit the fact that for $S_{3}$, there exist two optimal AB-schedules which finish twelve jobs in time 12, namely 4 A-patterns as well as 3 B-patterns. This fact provides some flexibility for designing optimal schedules for general bipartite graphs.

3.2 Optimal Schedules for Bipartite Graphs for a Given Star Forest

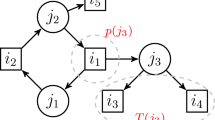
While we can restrict our attention to AB-schedules for stars, this property does not generalize to all bipartite graphs. In fact, it does not even hold for trees as illustrated in Fig. 3.

Observation 4

There exists a tree T such that no optimal schedule for smc-Unit (T, n) is an AB-schedule with respect to T.

Interestingly, the optimal schedule shown in Fig. 3 is comprised of two AB-schedules on the two stars obtained by deleting the gray edge. Combining this insight with the optimality of AB-schedules for stars is the basis of our divide-and-conquer algorithm. The key idea is to find a spanning subgraph H of G for which optimal AB-schedules with respect to H are among the optimal schedules for G. In particular, we identify subgraphs consisting of stars for which feasibility of AB-schedules can be encoded by certain vertex colorings of G. To do so, we introduce the following notions.

Star Forests and I, II, III-Colorings. A subgraph H of a graph G is a star forest of G if each component of H is a star and H contains all vertices of G.

We consider a star forest H of a bipartite graph G. In particular, we want to use specific vertex subsets of H, denoted by $A_i$ and $B_i$, to process the jobs. The idea is to schedule A-patterns on the $A_i$’s and B-patterns on the $B_i$’s.

A vertex subset $A_1$ is a I-coloring of (G, H) if it is a maximum independent set of both G and H. A I-coloring allows to schedule an A-pattern on H (by placing one job on each machine in $A_1$), yielding a valid schedule for G, see Fig. 4 (left).

Fig. 4.

A graph and a star forest with a I-, II-, and III-coloring and corresponding schedules. Vertices in $A_i$ are colored in asparagus and vertices in $B_i$ in blue. (Color figure online)

Two disjoint vertex subsets $A_2,B_2$ are a II-coloring of (G, H), if no vertex of $A_2$ is adjacent to another vertex from $A_2\cup B_2$ in G and the following properties hold: (i) for each $S=S_{\ell }$, $\ell \ge 3$, $A_2\cap S$ is a maximum independent set of S, (ii) $B_2$ contains the vertices of each $S_{1}$, and (iii) for each $S_{2}$, either $A_2\,\cap \,S_2$ is a maximum independent set of $S_{2}$ or $B_2$ contains the vertices of $S_{2}$. A II-coloring allows to schedule 3 A-patterns on stars with leaves in $A_2$ and 2 B-patterns on stars with vertices in $B_2$, see Fig. 4 (middle).

Two disjoint vertex subsets $A_3,B_3$ are a III-coloring of (G, H), if no vertex of $A_3$ is adjacent to another vertex from $A_3\cup B_3$ in G and the following properties hold: (i) for each $S=S_{\ell }$, $\ell \ge 4$, $A_3\cap S$ is a maximum independent set of S, (ii) $B_3$ contains the vertices of each $S_{1}$ and each $S_{2}$, and (iii) for each $S_{3}$, $A_3\cap S_{3}$ is a maximum independent set of $S_{3}$ or $B_3$ contains the vertices of $S_{3}$. A III-coloring allows to schedule 4 A-patterns on stars with leaves in $A_{3}$ and 3 B-patterns on stars with vertices in $B_{3}$, see Fig. 4 (right).

Star forests and I, II, III-colorings help us to extend the structural insights on stars to general bipartite graphs. Particularly, we show that an optimal schedule on a star forest admitting I, II, III-colorings also yields a feasible schedule with respect to G and is, therefore, also optimal.

Lemma 5

Let H be a star forest of a connected bipartite graph G on at least two vertices. Given a I-coloring $A_1$, a II-coloring $(A_2,B_2)$ and a III-coloring $(A_3,B_3)$ of (G, H), there exists a polynomial time algorithm to compute an optimal schedule for smc-Unit $(G,n)$.

Proof-Sketch

Let $\varPi '$ be an optimal schedule for smc-Unit $(G,n)$. By Lemma 3, there exists an optimal AB-schedule $\varPi$ for smc-Unit (H, n). Because H is a subgraph of G, we have $\Vert \varPi \Vert \le \Vert \varPi '\Vert$. We distinguish two cases.

If $\Vert \varPi \Vert \le 20$, we show that there exists an optimal AB-schedule $\varPi ^*$ on H that is feasible for G. The schedule $\varPi ^*$ is constructed as follows: Each A-pattern is scheduled on $A_1$, each B-pattern on V, 3 A-patterns on $A_2$, 2 B-patterns on $B_2$, 4 A-patterns on $A_3$, and 3 B-patterns on $B_3$.

If $\Vert \varPi \Vert \ge 21$, we show that each star on H contains either 4 A or 3 B patterns. Iteratively, shifting these to the front, we obtain a rest schedule of makespan at most 20. We thus need to compare 20 schedules to compute the optimal schedule.

   $\square$

To complete the proof of Theorem 4, it remains to show how to find a star forest and the corresponding colorings.

3.3 Computing a Star Forest with I, II, III-Colorings

We compute such a star forest and corresponding I, II, III-colorings in four phases. First, we find an initial star forest H admitting a feasible I-coloring. Then, we modify H in two phases to ensure the existence of a II- and III-coloring of the star forest, respectively. Finally, we compute all colorings. Modifications of the initial star forest are necessary because of the possible appearance of so-called alternating paths.

Alternating Paths. Let $H=(V,E')$ be a star forest of a bipartite graph $G=(V,E)$. Let $C_1,\ldots ,C_k$ be distinct stars of H and P be a path in G on the vertices $v_1,v_2\dots , v_{2k-1}$ with the following properties:

• for even i, $v_i$ is a leaf of star $C_{i/2+1}$,

• for odd i, $v_i$ is the center of star $C_{ (i+1)/2}$, and

• the edge $\{v_i,v_{i+1}\} \in E'$ if and only if i is even.

We say P is an alternating path of type II if $C_1\simeq S_{1}$, $C_i\simeq S_{2}$ for all $i=2,\dots ,k-1$ and $C_k\simeq S_{\ell }$ with $\ell \ge 3$. For an illustration of an alternating path of type II, see Fig. 5 (left).

Fig. 5.

Alternating path of type II. Black edges belong to H, gray edges to $G{\setminus }H$. (Color figure online)

We say P is an alternating path of type III if $C_1\simeq S_{2}$, $C_i\simeq S_{3}$ for all $i=2,\dots ,k-1$ and $C_k\simeq S_{\ell }$ with $\ell \ge 4$, see also Fig. 6 (left).

Fig. 6.

Alternating path of type III. Black edges belong to H, gray edges to $G{\setminus }H$. (Color figure online)

If an alternating path of type II (III) exists in the star forest, then there is no feasible II-coloring $(A_2,B_2)$ (III-coloring $(A_3,B_3)$), as $B_2$ ($B_3$) must contain all nodes of the first star $C_1$, and hence also the nodes of all intermediate stars leading to adjacent vertices $v_{2k-3}\in B_2$ ($B_3$) and $v_{2k-2}\in A_2$ ($A_3$). However, an alternating path can be removed by swapping edges along it; this operation maintains the leaves of the star forest, see Figs. 5 and 6 (right).

Observation 6

Let $H=(V,E')$ be a star forest of G containing an alternating path P of type II or III. Then, $H':=(V,E'\varDelta P)$ is a star forest with the same set of leaves as H, where $\varDelta$ denotes the symmetric difference.

Algorithm 1 computes a star forest and I,II,III-colorings in polynomial time.

Lemma 7

Algorithm 1 returns a star forest H of G and I-,II- and III- colorings $A_1,(A_2,B_2)$ and $(A_3,B_3)$ of (G, H), respectively, in time polynomial in G.

Proof

We first show that Algorithm 1 is well-defined (specifically line 7) and that the graph H, defined in line 16, is a star forest. Let M be a maximum matching and I be a maximum independent set of G. Both can be found in polynomial time using the maximum flow algorithm to find a maximum matching in bipartite graphs [34, Theorem 10.5]. Observe that the complement of a maximum independent set is a minimum vertex cover $U:=V{\setminus }I$. By Kőnig’s Theorem [32], it holds that $|U|=|M|$. In particular, every edge in M contains exactly one vertex of U and every vertex in $V' := V{\setminus }\bigcup _{e \in M} e$ is not contained in U. Therefore, for every $v\in V'$, there exists $u\in U$ such that $\{u,v\}\in E$, i.e., line 7 in Phase 1 is well-defined. By Lemma 6, modifying the star forest $(V,E')$ along an alternating path in Phase 2 and 3 results again in a star forest. It remains to show that $(V,E')$ is a star forest at the end of Phase 1. To this end, note that every edge of $E'$ is incident to exactly one vertex $u\in U$. Thus, every vertex in U is the center of a star (on at least 2 vertices).

For the runtime, it is important to observe that in every iteration of Phase 2 (Phase 3), some $S_1$ ($S_2$) is removed and no new $S_1$ ($S_2$) is created. Therefore, the number of iterations in Phase 2 (Phase 3) is bounded by the number of $S_1$’s ($S_2$’s) before Phase 2 (Phase 3). An alternating path of type II (type III) can also be found in polynomial time by using BFS starting from a fixed $S_{1}$ ($S_{2}$). Because Phase 4 clearly runs in polynomial time, Algorithm 1 does as well.

Finally, we prove that Phase 4 computes valid colorings. Here, we exploit the fact that no alternating path of type II is created in Phase 3 (Lemma 16). Thus, after Phase 3, there exists no alternating path (of any type).

By definition, $A_1:=I$ is a maximum independent set of G. We argue that $A_1$ is also an maximum 1-IS of H. Note that while U constitutes the centers of the stars, $V{\setminus } U=I=A_1$ are the leaves of the stars after Phase 1. Hence the claim is true after Phase 1. Lemma 6 ensures that this property is maintained in Phase 2 and 3. Hence, $A_1$ is a I-coloring.

For the type II-coloring, the algorithm ensures that $A_2$ contains the leaves of all $S_{\ell }$ with $\ell \ge 3$ and that $B_2$ contains all vertices of $S_1$. Hence, we only need to pay attention to $S_2$’s. The algorithm inserts the leaves of stars $S_{2}$ into $A_2$ if their center is adjacent to a vertex in $A_2$, as long as it is possible. The vertices of all remaining $S_2$’s are inserted into $B_2$. Thus, the properties (i), (ii) and (iii) of a II-coloring are fulfilled by $(A_2,B_2)$. It only remains to show that no vertex of $A_2$ is adjacent to another vertex of $A_2\cup B_2$ in G. Because $A_2\subset I$, no two vertices in $A_2$ are adjacent in G. Suppose there is a vertex $a\in A_2$ adjacent in G to a vertex $b\in B_2$. Let $S^a$ and $S^b$ be the star containing a and b, respectively. By construction a is a leaf of $S^a$. Moreover, $b\in U$; otherwise $a,b\in A_1$, a contradiction to the fact that $A_1$ is an independent set. If $S^b\simeq S_2$, then the center b is adjacent to $a\in A_2$, and the algorithm ensures that the leaves of $S^b$ are contained in $A_2$, and hence, $b\notin B_2$. Thus, $S^b\simeq S_1$.

If $S^a\simeq S_\ell ,\ell \ge 3$, then there exists an alternating path of type II starting in b and ending in the center of $S^a$, a contradiction.

If $S^a\simeq S_2$, the fact $a\in A_2$ implies that there exists a star $S_\ell$, $\ell \ge 2$, with a leaf adjacent to the center of $S^a$. If $\ell =2$, there exists a further star whose leaf is adjacent to the considered star. Repeating this argument, the containment of $a\in A_2$ can be traced back to a star $S_\ell ,\ell \ge 3$, and yields an alternating path of type II, a contradiction.

With arguments similar to the above, $(A_3,B_3)$ is a III-coloring; otherwise we find an alternating path of type III. Specifically, one can show that vertex a belongs to a star $S_2$ and b to a star $S_3$.    $\square$

Finally, Theorem 4 follows from Lemmas 1, 5 and 7.

4 Future Directions

Various interesting avenues remain open for future research. In particular, the investigation of graph classes capturing geometric information is of special interest for applications in which spatial proximity causes machines conflicts. Additionally, allowing for preemption constitutes an interesting direction.

5 Appendix I – Details for Sect. 2

All theorems in Sect. 2 are divided into two cases: either all jobs have long blocking times ( ) or short blocking times ( ). We split the proofs up according to the relation between the parameters and present the results in two subsections. Specifically, Theorem 1 follows from Theorem 5 and Theorem 8. Theorem 2 follows from Theorem 6 and Theorem 9. Theorem 3 follows from Theorem 7 and Theorem 10. Throughout the remainder, we denote the optimal makespan of a given instance by $\textsc {opt}$.

5.1 Long Blocking Times

In this subsection, we consider smc-Id where jobs have long blocking times, i.e., it holds . These long blocking times lead to so-called basic schedules in which jobs on conflicting machines do not run in parallel.

Basic Schedules. A schedule $\varPi$ is basic, if for every edge $ii'\in E$ and for every pair of jobs j and $j'$ assigned to i and $i'$, respectively, their system times are non-overlapping, i.e., $S_j^{\varPi }\le S_{j'}^{\varPi }$ implies $C_j^{\varPi } \le S_{j'}^{\varPi }$.

The following lemma allows us to focus on basic schedules.

Lemma 8

For an instance of $\textsc {smc-Id}$, every schedule $\varPi$ is basic if

Proof

Suppose for the sake of a contradiction that there exists two jobs j and $j'$ assigned to machines i and $i'$, respectively, with $ii'\in E$ such that $j'$ starts while j is processed. Because their blocking times cannot overlap, we also know that $j'$ starts after the first blocking time of j and the first blocking time of $j'$ ends before the second blocking time of j starts, see Fig. 7. Consequently, . Moreover, if $j'$ ends after j.

Fig. 7.

Illustration of the proof of Lemma 8.

Because all jobs have the same parameters, we obtain the contradiction and .    $\square$

In the following, we present the proof of Theorem 1 for the case of long blocking times. To this end, for instances of smc-Id we denote by $\alpha _1$ the cardinality of a maximum independent set of G.

Theorem 5

[Theorem 1 for long blocking times]. Unless $\text {P} =\text {NP}$, smc-Id where are fixed and holds does not admit a $\mathcal {O}(m^{1-\varepsilon })$-approximation for any $\varepsilon > 0$.

Proof

We restrict our attention to instances consisting of $n=\alpha _1$ jobs and for the sake of simplicity let by scaling. By Lemma 8, schedules for smc-Id with are basic. Clearly, the optimum makespan opt is 1 because $q = 1$. Suppose for some constant $\kappa > 0$ there exists a $(\kappa m^{1-\varepsilon })$-approximation algorithm for $\varepsilon > 0$ and let $\varPi$ denote its schedule. Moreover, let $\beta$ denote the maximum number of machines processing jobs in parallel in $\varPi$ at any point in time. As we have at most n distinct starting times in $\varPi$ we can compute $\beta$ in polynomial time. Because $\varPi$ is basic, we can transform $\varPi$ into a new schedule $\varPi '$ that processes all jobs non-idling on $\beta$ machines without increasing the makespan. Hence, we obtain $\Vert \varPi \Vert \ge \left\lceil n/\beta \right\rceil \ge n/\beta$. This fact together with the assumption $\Vert \varPi \Vert \le \kappa m^{1-\varepsilon } \cdot \textsc {opt} =\kappa m^{1-\varepsilon }$ yields $\beta \ge n/\Vert \varPi \Vert \ge n/\kappa m^{1-\varepsilon }=1/\kappa m^{1-\varepsilon }\cdot \alpha _1$. In other words, the $(\kappa m^{1-\varepsilon })$-approximation algorithm implies an $(1/\kappa \cdot m^{\varepsilon -1})$-approximation algorithm for computing a maximum 1-IS for every graph G; a contradiction [24, 42].    $\square$

We now present the proofs of Theorems 2 and 3 for long blocking times, respectively.

Theorem 6

[Theorem 2 for long blocking times]. Let G be a graph. If and we are given a 1-IS of G, then an optimal schedule of smc-Id can be computed in polynomial time.

Proof

Let $\varPi$ be an optimal schedule for smc-Id with . By Lemma 8, $\varPi$ is basic, hence, at any point in time at most $\alpha _1$ jobs are running. Therefore, we can modify the job-to-machine assignment of $\varPi$ such that all jobs are processed on a maximum 1-IS while maintaining the starting times of the jobs. As we did not increase the makespan, we have an optimal schedule where all jobs are assigned to a maximum 1-IS. Because all jobs are identical, evenly distributing all jobs over the machines yields an optimal schedule.    $\square$

Theorem 7

[Theorem 3 for long blocking times]. Let G be a graph. If and we are given a $1/\gamma$-approximate 1-IS of G, then smc-Id allows for a $\lceil \gamma \rceil$-approximation.

Proof

Let $\mathcal I$ denote the given $1/\gamma$-approximate 1-IS, i.e., $|\mathcal {I}|\ge \alpha _1/\gamma$. Without loss of generality we assume . An optimal schedule distributes all jobs evenly over a maximum 1-IS, i.e., we have $\textsc {opt} = \left\lceil n/\alpha _1\right\rceil$ as $q=1$. Since each system time is 1, we can find a schedule $\varPi$ with makespan $\Vert \varPi \Vert = \left\lceil n/|\mathcal {I} | \right\rceil \cdot q \le \left\lceil \gamma \cdot n/\alpha _1 \right\rceil \le \lceil \gamma \rceil \cdot \left\lceil n/\alpha _1\right\rceil = \lceil \gamma \rceil \cdot \textsc {opt}$ by distributing all jobs evenly on $\mathcal {I}$.    $\square$

5.2 Short Blocking Times

In this subsection, we consider smc-Id where jobs have short blocking times, i.e., it holds . By symmetry, we assume that and hence, we write . We first introduce a generalized notion of independent sets.

(Maximum) Induced c-Colorable Subgraph. For a graph $G=(V,E)$ and $c\in \mathbb {N}_{\ge 1}$, a maximum induced c-colorable subgraph, or short maximum c-IS, of G is a set of c disjoint independent sets $\mathcal {I} _1,\ldots ,\mathcal {I} _c \subseteq V$ whose union has maximum cardinality. Clearly, a 1-IS is an independent set. Moreover, the cardinality of a maximum c-IS is defined as the cardinality of the union of $\mathcal {I} _1,\ldots ,\mathcal {I} _c$. We denote the cardinality of a maximum c-IS by $\alpha _c$. These c-ISs can be used to obtain useful partial schedules.

c-Pattern. Let $c\in \mathbb {N}_{\ge 1}$ with and let $\mathcal {I}=(I_1,I_2,\dots , I_c)$ be a c-tuple of disjoint independent sets of G. Recall that denotes the system time. A partial schedule of length starting at time t is called a c-pattern on $\mathcal {I}$ if on each machine i in $I_k$ with $k \in \{1,\dots ,c\}$, there is one job starting at time .

In order to show connections between conflict-free schedules and c-ISs, we extract a c-IS from a conflict-free schedule. We say a job j blocks a time t in schedule $\varPi$ if one of its blocking times contains t, i.e., . For a schedule $\varPi$, we define the quantity

$$ \beta _c^{\varPi }:=\max _{t_1< \ldots <t_c} \left\{ \left| \bigcup _{k=1}^c \left\{ i\in V: i\text { processes a job in } \varPi \text { which blocks time } t_k\right\} \right| \right\} . $$

Observe that for each time t the machines which process a job blocking time t form an 1-IS, because $\varPi$ is conflict-free. Hence, $\beta _c^{\varPi }$ corresponds to the cardinality of a c-IS, since machines are not counted more than once. It is easy to see that $\beta _c^{\varPi }$ can be computed in polynomial time for a constant c.

Lemma 9

For a schedule $\varPi$ with n jobs and a constant c, $\beta _c^{\varPi }$ can be computed in time polynomial in n.

Proof

The schedule has 4n event times, namely the starting time of the blocking times and the processing time and its completion time for each job. For some point in time t between every two consecutive event points, we count the number of machines processing a blocking interval. By definition of $\beta _{c}^\varPi$, it suffices to check $\mathcal {O}(n^{c})$ tuples.    $\square$

The definition of $\beta _{c}^{\varPi }$ helps us to bound the makespan of a schedule $\varPi$ from below stated in Lemma 12. To this end, we first give an upper bound on the number of jobs starting within an interval of length $\lambda$ which is defined as follows. For instances of smc-Id with , we define

Lemma 10

For every schedule $\varPi$ of an instance smc-Id with and every time $t\ge 0$, the number of jobs starting within the interval $I:=[t, t+\lambda )$ is at most $\beta _{k +1}^{\varPi }$.

Proof

Because I has length $\lambda \le q$ and is half-open, at most one job starts on each machine within I. We partition the interval I into an (possibly empty) interval $I_0$ (left-closed, right-open) of length (evaluating to if and to 0 otherwise) and $k+1$ disjoint (left-closed, right-open) intervals $I_1,\dots ,I_{k+1}$, each of length . Clearly, the length of the intervals $I_0,\dots , I_{k+1}$ add to $\lambda$. By $V_{\ell }$ we denote the set of machines that have a job starting in $I_{\ell }$. For each $\ell$, the jobs processed on a machine in $V_{\ell }$ block a point in time arbitrarily close to the right end of $I_\ell$, see Fig. 8 (left). Thus, all $V_\ell$’s are independent sets.

Fig. 8.

Illustration for the proof of Lemma 10: (left) two jobs starting in $I_1$ and (right) a job starting in $I_0$ and a job starting in $I_{k+1}$.

Additionally, we show that $V_0\cup V_{k+1}$ is an independent set. If , then $V_0=\emptyset$. It thus remains to consider the case . Let $t'$ be a point in time arbitrarily close to the right end of interval I. The second blocking time of job j processed on a machine in $V_0$ starts in interval , and thus starts before $t+q$ and ends not before $t+q$. Hence $t'$ is blocked by the second blocking time of j. Additionally, observe that $t'$ is blocked by the first blocking time of every job processed on a machine in $V_{k+1}$, see also Fig. 8 (right). Consequently, each $V_\ell$ and $V_0\cup V_{k+1}$ are independent sets and thus, the number of jobs can be bounded from above by $\beta _{k+1 }^{\varPi }$.    $\square$

Next, we show that an upper bound on the number of jobs starting within an interval of a specific lengths implies a lower bound on the makespan.

Lemma 11

Let $\varPi$ be a schedule for an instance smc-Id with such that for some integer $\beta$, in every interval of length $L \le q$ at most $\beta$ jobs start. Then, for system time , it holds that

$$\Vert \varPi \Vert \ge L \lfloor n/\beta \rfloor + {\left\{ \begin{array}{ll} 0&{} \text {if }\beta \text { divides } n\\ q&{} \text {otherwise.} \end{array}\right. } $$

Proof

We divide $\varPi$ into intervals of length L starting with 0. By assumption, at most $\beta$ jobs start in each interval. Hence, the number of these intervals (where some job is processed) is at least $\lfloor n/\beta \rfloor$. Moreover, if $\beta$ does not divide n, then at least some job (of length q) starts after time $L\lfloor n/\beta \rfloor +q$.    $\square$

Lemma 10 and 11 immediately imply a lower bound on the makespan of any schedule.

Lemma 12

For every schedule $\varPi$ for an instance of smc-Id with , the makespan is at least $\Vert \varPi \Vert \ge \lambda \cdot \lceil n/\beta _{k+1}^{\varPi }\rceil$. In particular, the optimal makespan is bounded from below by $\textsc {opt} \ge \lambda \cdot \lceil n/\alpha _{k+1}\rceil$.

Using Lemma 12, we prove Theorem 1 for short blocking times.

Theorem 8

[Theorem 1 for short blocking times]. Unless $\text {P} =\text {NP}$, smc-Id where are fixed and holds does not admit a $\mathcal {O}(m^{1-\varepsilon })$-approximation for any $\varepsilon > 0$.

Proof

Suppose that for some $\kappa >0$ and some $\varepsilon > 0$ there exists a $(\kappa m^{1-\varepsilon })$-approximation algorithm $\mathcal A$. We assume and define and $\lambda$ as above. For an instance of smc-Id with short blocking times and $n\ge \alpha _{k+1}$, we consider the schedule $\varPi$ computed by $\mathcal A$. On the one hand, because $\mathcal A$ is a $(\kappa m^{1-\varepsilon })$-approximation, $\varPi$ has makespan

$$ \Vert \varPi \Vert \le (\kappa m^{1-\varepsilon }) \cdot \textsc {opt}. $$

On the other hand, by Lemma 12, we have

$$ \Vert \varPi \Vert \ge \lambda \cdot \left\lceil n/\beta _{k+1}^{\varPi }\right\rceil \ge \lambda n\cdot 1/\beta _{k+1}^{\varPi }. $$

Moreover, we obtain a feasible schedule by repeatedly using $(k +1)$-patterns on a maximum $(k +1)$-IS, while leaving the other machines idle. Recall that a $(k +1)$-pattern has length and schedules $\alpha _{k+1}$ jobs. This yields the upper bound

where the last inequality uses the fact $n/\alpha _{k+1}\ge 1$ and thus $\lceil n/\alpha _{k+1}\rceil \le 2(n/\alpha _{k+1})$. Altogether, we obtain

where is a constant $\le 1$ since $\lambda \le q$. By Lemma 9, we can compute a $(k+1)$-IS from $\varPi$ of size $\beta _{k+1}^\varPi$ in polynomial time and thus we obtain a $\mathcal {O}(m^{\varepsilon -1})$-approximation for computing a maximum $(k+1)$-IS; a contradiction [24, 36, 42].

   $\square$

We now provide the proofs of Theorems 2 and 3 for short blocking times.

Theorem 9

[Theorem 2 for short blocking times]. If and we are given a maximum -IS of G, then smc-Id allows for a -approximation, with and if , we even get .

Proof

We define a schedule $\varPi$ consisting of $\left\lceil n/\alpha _{k+1}\right\rceil$ many $(k+1)$-patterns on a maximum $(k+1)$-IS of G, while leaving all other machines idle. $\varPi$ has makespan . By Lemma 12, it holds that $\textsc {opt} \ge \lambda \cdot \left\lceil n/\alpha _{k+1}\right\rceil$. We obtain

   $\square$

Theorem 10

[Theorem 3 for short blocking times]. If and we are given a $1/\gamma$-approximate -IS of G, then smc-Id allows for a -approximation, with . If , we get .

Proof

Let $\mathcal I$ be the given $(k+1)$-IS of size $\beta \ge \alpha _{k+1}/\gamma$. We construct a schedule $\varPi$ by using $\left\lceil n/\beta \right\rceil$ many $(k+1)$-patterns on $\mathcal I$ which has makespan . Moreover, Lemma 12 implies $\textsc {opt} \ge \lambda \cdot \left\lceil n/\alpha _{k+1}\right\rceil \ge \lambda \cdot n/\alpha _{k+1}$. If $n\le \beta$, then also $n\le \alpha _{k+1}$, implying that$\left\lceil n/\beta \right\rceil =\left\lceil n/\alpha _{k+1}\right\rceil =1$. Thus, we obtain

Hence, following the same steps as in the proof of Theorem 9, we obtain an upper bound on the performance guarantee of 2 if and 2.5 if . If $n > \beta$, we obtain $\left\lceil n/\beta \right\rceil \le 2\cdot n/\beta \le 2\gamma \cdot n/\alpha _{k+1}$. Consequently, it holds

Again, following the same steps as in the proof of Theorem 9, we obtain an upper bound on the performance guarantee of $4\gamma$ if and $5\gamma$ if .    $\square$

6 Appendix II – Details for Sect. 3

In the following we provide omitted proofs of Sect. 3.

Lemma 1

For every n, an optimal schedule for smc-Unit $(K_m,n)$ can be computed in time linear in $\log n$. In particular, for $m\ge 2$, it coincides with an optimal schedule for $K_2$ of makespan $4\lfloor n/2\rfloor +3(n \mod 2)$.

Proof

Let $\varPi$ be an optimal schedule of smc-Unit $(K_m,n)$. Note that for each point in time t, the set of machines processing a job at time t induces a $K_1$ or $K_2$. Moreover, all vertices in $K_m$, $m\ge 2$, play the same role and hence we may shift all jobs to the same two vertices. Thus, we may reduce our attention to smc-Unit $(K_2,n)$. It is easy to check that two jobs are optimally processed in time 4. This implies the claim.    $\square$

The next lemma shows that we can restrict to schedules with integral starting times.

Lemma 13

If , $p_j$, are integral for all $j\in \mathcal {J}$, every feasible schedule $\varPi$ can be transformed into a feasible schedule $\varPi ^*$ such that the starting time of each job is intergral and the makespan does not increase, i.e., $\Vert \varPi ^*\Vert \le \Vert \varPi \Vert$.

Proof

Let $S_j^{\varPi }$ denote the starting time for each job $j\in J$. We define $\varPi ^*$ by $S_j^{\varPi ^*}:=\lfloor S_j^{\varPi }\rfloor$ for each job j. It remains to show that $\varPi ^*$ is feasible. Let j and $j'$ be two jobs such that two of their blocking times b and $b'$ intersect in ${\varPi ^*}$. By integrality of $\varPi ^*$ and the blocking times, they intersect in at least one time unit.

Without loss of generality, we assume that $b'$ does not start before b in $\varPi$. With slight abuse of notation, $S_{b}^\varPi$ denotes the starting time of the blocking time b in $\varPi$. Then, $S_{b'}^\varPi -S_{b}^\varPi$ and $S_{b'}^{\varPi ^*}-S_{b}^{\varPi ^*}$ differ by strictly less than 1. Hence, if they intersect in at least 1 time unit in $\varPi ^*$, then they also intersect in $\varPi$. Therefore, by feasibility of $\varPi$, j and $j'$ are scheduled on conflict-free machines.    $\square$

Corollary 1

For every star S and every n, an optimal schedule for smc-Unit (S, n) can be computed in time linear in $\log n$ and |S|.

Specifically, for every $S_\ell$, there exists $X\in \{A,B\}$ such that an optimal schedule has at most 2 X-patterns, i.e., an optimal schedule has makespan

$$\begin{aligned} \min _{k=0,1,2} \left\{ 4\bigg \lceil \frac{n-k\ell }{\ell +1}\bigg \rceil +3k, 3\bigg \lceil \frac{n-k(\ell +1)}{\ell }\bigg \rceil +4k \right\} , \end{aligned}$$

(2)

where $\lceil \cdot \rceil$ denotes the usual ceiling function; however, for negative reals it evaluates to 0.

Proof

By Lemma 3, there exists an optimal AB-schedule. For a star $S_\ell$, an A-pattern processes $\ell$ jobs in time 3 and a B-pattern processes $(\ell +1)$ jobs in time 4. An AB-schedule for at least n jobs with exactly k A-patterns has a makespan of $4\lceil \frac{n-k\ell }{\ell +1}\rceil +3k$. Similarly, an AB-schedule for at least n jobs with exactly k B-patterns has a makespan of $3\lceil \frac{n-k(\ell +1)}{\ell }\rceil +4k$.

For $\ell \le 2$, an optimal schedule contains at most 2 A-patterns. While 3 A-patterns process $3\ell$ jobs in time 9, 2 B-pattern process $2(\ell +1)\ge 3\ell$ jobs in time 8. Thus, any 3 A-patterns can be replaced by 2 B-patterns.

For $\ell \ge 3$, an optimal schedule contains at most 2 B-patterns: While 3 B-patterns process $3(\ell +1)$ jobs in time 12, 4 A-patterns finish $4\ell \ge 3(\ell +1)$ jobs in time 12. Thus, any 3 B-patterns can be replaced by 4 A patterns.

Therefore, for each star we only have to compare at most three different schedules with $k=0,1,2$ A- or B-patterns, respectively. Taking one with minimum makespan induces an optimal solution.    $\square$

We next present the full proof of Lemma 5.

Lemma 5

Let H be a star forest of a connected bipartite graph G on at least two vertices. Given a I-coloring $A_1$, a II-coloring $(A_2,B_2)$ and a III-coloring $(A_3,B_3)$ of (G, H), there exists a polynomial time algorithm to compute an optimal schedule for smc-Unit $(G,n)$.

Proof

Let $\varPi '$ be an optimal schedule for smc-Unit $(G,n)$. By Lemma 3, there exists an optimal AB-schedule $\varPi$ for smc-Unit (H, n). Because H is a subgraph of G, we have $\Vert \varPi \Vert \le \Vert \varPi '\Vert$. First, we show how to solve smc-Unit $(G,n)$ for small optimal makespan values.

Claim 14

If $\Vert \varPi \Vert \le 20$, then there exists an optimal AB-schedule $\varPi ^*$ on H that is feasible for G (according to Table 1).

Table 1. AB-schedules on the stars of H based on Corollary 1 and modification *. The number before A and B indicates the number of A- and B-patterns.

To prove this claim, observe that $\Vert \varPi \Vert \ge q =3$ and that there is no AB-schedule with $\Vert \varPi \Vert =5$. We first show how to define a schedule $\varPi ^*$ of makespan $\Vert \varPi \Vert$ according to Table 1 that has as many jobs as $\varPi$. Afterwards, we show that $\varPi ^*$ is feasible with respect to G. To this end, we first concentrate on the four types of components in H. For $C\in \{S_1,S_2,S_3,S_{\ell \ge 4}\}$, let $L_{C}$ denote the set of all makespan (of at most 20) from schedules obtained by Corollary 1. For $C\in \{S_1,S_2,S_3,S_{\ell \ge 4}\}$ and $\Vert \varPi \Vert \in [20]\setminus \{1,2,5\}$, we use the optimal AB-schedule with makespan $\Vert \varPi \Vert$ (or the maximum value in $L_C$ that is $\le \Vert \varPi \Vert$). However, we modify some schedules in order to guarantee feasibility later: modified entries are marked by an asterisk in Table 1.

For $S_1$ and for $\Vert \varPi \Vert \equiv 2 \pmod {4}$, we use 2 A-patterns and $(\lfloor \Vert \varPi \Vert /4\rfloor -1)$ B-patterns instead of $\lfloor \Vert \varPi \Vert /4\rfloor$ B-patterns. Since 2 A-patterns and 1 B-pattern differ in length 2, the modified schedule finishes within $\Vert \varPi \Vert$. It also schedules at least as many jobs as $\varPi$, because 1 A-pattern contains one job while 1 B-pattern contains two jobs.

For $S_2$ and for $\Vert \varPi \Vert \equiv 1 \pmod {4}$, we also allow to schedule 3 A-patterns and $\lfloor \Vert \varPi \Vert /4\rfloor -2$ B-patterns besides the optimal schedule using $\lfloor \Vert \varPi \Vert /4\rfloor$ B-patterns. As 3 A-patterns and 2 B-patterns differ in length 1, the modified schedule finishes within $\Vert \varPi \Vert$. Moreover, both 3 A-patterns and 2 B-patterns contain six jobs.

Table 1 displays the resulting patterns on the components. The schedule $\varPi ^*$ is constructed as follows: Each A-pattern is scheduled on $A_1$, each B-pattern on V, 3 A-patterns on $A_2$, 2 B-patterns on $B_2$, 4 A-patterns on $A_3$, and 3 B-patterns on $B_3$. It remains to show that scheduling according to Table 1 is feasible with respect to G.

By definition of $A_1$, scheduling an A-pattern on $A_1$ yields a feasible schedule for smc-Unit $(G,n)$. This is used for the A-patterns in the cases where $\Vert \varPi \Vert \in \{3,6,10,11,14,15,18,19\}$.

Because G is bipartite, a B-pattern can be scheduled on V. This is used for the B-patterns in the cases where $\Vert \varPi \Vert \in \{4,7,8,10,11,13,14,16,17,19,20\}$.

Because $(A_2,B_2)$ is a II-coloring, scheduling 3 A-patterns on $A_2$ and 2 B-patterns on $B_2$ is feasible. This is used for the case where $\Vert \varPi \Vert \in \{9,13,17\}$.

Because $(A_3,B_3)$ is a III-coloring, scheduling 4 A-patterns on $A_3$ and 3 B-patterns on $B_3$ is feasible. We use this whenever $\Vert \varPi \Vert \in \{12, 15, 16, 18, 19, 20\}$. This proves Claim 14.

Claim 15

There exists an optimal schedule that is comprised of blocks of length 12 following row 12 of Table 1 and one rest block of length at most 20 following Table 1.

By Claim 14, we need to show Claim 15 for $\Vert \varPi \Vert \ge 21$. We may assume that for any two different components of H, their makespans in $\varPi$ differ by at most 3. Suppose there exists components $C_1$ and $C_2$ such that the makespan of $C_1$ exceeds the makespan of $C_2$ by at least 4. Deleting a last job from $C_1$ and inserting it after the last job of $C_2$, the makespan difference decreases. As a consequence, the makespan in $\varPi$ on each component is at least 18. This implies that $\varPi$ schedules at least 4 A-patterns or 3 B-patterns both of length 12 on each connected component: Let C be a component of H. If $\varPi$ has at most 3 A-patterns and at most 2 B-patterns on C, then the makespan on C is at most $3\cdot 3+2\cdot 4=17$. A contradiction. Therefore, if $\Vert \varPi \Vert \ge 21$, we modify $\varPi$ by scheduling the 4 A-patterns on $A_3$ and the 3 B-patterns on $B_3$. By definition of a III-coloring of $(A_3,B_3)$ this yields a feasible subschedule with respect to G. We repeat this procedure until the makespan of the remaining patterns is at most 20. This proves Claim 15.

We can compute the schedule obtained by Table 1 for each possible value $r\in [20]\setminus \{1,2,5\}$ on each connected component using the given I-,II- and III-colorings and filling it up with blocks of 12 following row 12 of Table 1. By Lemma 15, the schedule with minimum makespan is an optimal schedule.   $\square$

In the following, we complete the proof of Lemma 7 by showing that modifying a star forest which does not contain any alternating paths of type II along an alternating path of type III will create a new star forest which also does not contain any alternating path of type II.

Lemma 16

Let $H=(V,E')$ be a star forest of G without any alternating paths of type II. Let P be an alternating path P of type III. Then the star forest $H'=(V,E'\varDelta P)$ contains no alternating paths of type II.

Proof

Let $C_{1}, \dots C_{k}$ be the stars of the alternating path P in H and let $C'_{1}, \dots C'_{k}$ denote the corresponding stars in $H'$. Observe that $C'_{i}\simeq C_i\simeq S_3$ for all $i\in \{2,\dots ,k-1\}$. Moreover, $C'_1=S_3$ and $C'_k=S_\ell$ for some $\ell \ge 3$. For the purpose of a contradiction, suppose that $H'$ contains an alternating path $P_2$ of type II. Clearly, $P_2$ and P intersect; otherwise $P_2$ is also contained in H. Specifically, $P_2$ ends in some $C'_i$ with $i\in \{1,\dots ,k\}$. If $i>1$, then $P_2$ and P share exactly the center of $C'_i$ and thus H contains $P_{2}$ as well. A contradiction. If $P_2$ ends in $C'_1$, then H contains an alternating path of type II ending in $C_2$ that goes via $C_1\simeq S_2$. Again, a contradiction.    $\square$