Keywords

1 Introduction

Careful planning of the individual surgical steps is an indispensable tool for the orthopedic surgeon, elevating the procedure’s safety and ensuring high levels of surgical precision [4, 6, 14, 15]. A surgical plan for routine interventions like ligament reconstruction describes several salient landmarks on a 2D X-ray image and relates them in a geometric construction [5, 8, 22]. Previous attempts to automate this planning type typically separate automatic feature localization with a learning algorithm and geometric post-processing [11,12,13]. The separation allows to mimic the manual step-wise workflow and enables granular control over each planning step. However, this approach comes with the drawbacks of optimizing a proxy criterion. While this surrogate has shown to be a low-error approximation of the actual planning target for well-aligned anatomy, the strength of correlation depends on the level of image truncation and the visibility of the contained radiographic landmarks [2, 24, 27]. In manual planning, the user compensates for these effects by extrapolating visual cues and using prior anatomical knowledge. As the learning algorithm has no direct access to this knowledge, the variance in correlation limits spatial generalization to unseen data with a broad range of image characteristics. In this work, we develop and analyze a companion objective function that optimizes the planning target directly. We exploit that the planning geometry can be formulated as a continuously differentiable function, enabling end-to-end gradient flow. Through the combination with the original optimization of anatomical feature localization, the relations of the planning geometry can be retained. We name this concept Deep Geometric Supervision (DGS). We test its effectiveness by studying the following research questions.

RQ 1.:

How does DGS affect the overall positioning accuracy?

RQ 2.:

Does DGS improve spatial generalisation on truncated images?

RQ 3.:

Can the potential improvements be applied to more complex imaging data in an intra-operative setting?

The developed method is evaluated for medial patellofemoral ligament (MPFL) reconstruction planning on diagnostic and intra-operative knee radiographs. This planning involves calculating the Schoettle Point (SP) [22], which determines the physiologically correct insertion point of the replacement graft and ensures long-term joint stability. We demonstrate that DGS significantly improves localization accuracy, increases the success rate of plannings to be within the required precision range of \(2.5\,\textrm{mm}\), and enables generalization to severely truncated images.

2 Materials and Methods

2.1 Automatic Approach to Orthopedic Surgical Planning

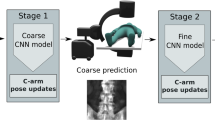
We build on the two-stage planning method proposed by Kordon et al. [12, 13]. First, the positions of salient anatomical landmarks are automatically extracted using a multitask learning (MTL) approach. Then, the landmarks are interrelated through geometric post-processing to locate the actual planning target.

Fig. 1.
figure 1

Overview of the proposed method to automatic surgical planning with DGS.

Full size image

In the first stage (Fig. 1-1), we want to optimize a mapping \(f_{\boldsymbol{\theta }}^{t}: \mathcal {X}\rightarrow \mathcal {Y}^{t}\) from the input domain \(\mathcal {X}\) to several task solution spaces \(\{\mathcal {Y}^{t}\}_{t\in [T]}\). \(\boldsymbol{\theta }\) marks a set of trainable function parameters, and \(T\) is the number of parallel tasks to solve. The function \(f_{\boldsymbol{\theta }}^{t}\) is optimized in a supervised manner using \(M\) datapoints \(\{x_{i}, y_{i}^{1}, \ldots , y_{i}^{T}\}_{i\in [M]}\) with ground truth \(y_{i}^{t}\). To exploit similarities between tasks and maintain task-specific complexity at the same time, we employ hard parameter-sharing [3, 21]. Therefore, the model capacity \(\boldsymbol{\theta }\) is separated into disjoint sets of shared parameters \(\boldsymbol{\theta }^{sh}\) and task-specific parameters \(\{\boldsymbol{\theta }^{t}\}_{t\in [T]}\). According to Baxter [1], this separation can be interpreted as a subdivision of function \(f_{\boldsymbol{\theta }}^{t}\) into a meta learner \(f_{\boldsymbol{\theta }^{sh}}^{\text {meta}}: \mathcal {X}\rightarrow \mathcal {Z}\) and task-specific learners \(f_{\boldsymbol{\theta }^{t}}^{\text {task},t}: \mathcal {Z}\rightarrow \mathcal {Y}^{t}\), such that the composition \((f_{\boldsymbol{\theta }^{t}}^{\text {task},t} \circ f_{\boldsymbol{\theta }^{sh}}^{\text {meta}})=f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}}^{t}: \mathcal {X}\rightarrow \mathcal {Y}^{t}\). The task-specific parameters can be trained by minimizing the loss function \(\mathcal {L}^{t}_{\text {Proxy}}(\cdot ,\cdot ):\mathcal {Y}^{t}\times \mathcal {Y}^{t}\rightarrow \mathbb {R}^{+}_{0}\). Following common practice in MTL literature, the shared parameters of the meta learner are optimized using a linear combination of all task losses [23]. Using this rationale, we arrive at the empirical risk minimization (ERM) objective

$$\begin{aligned} \min _{\boldsymbol{\theta }^{sh};\,\boldsymbol{\theta }^{1}, \ldots , \boldsymbol{\theta }^{T}} \sum \nolimits _{t=1}^{T}\hat{\mathcal {L}}^{t}_{\text {Proxy}}(\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}), \end{aligned}$$
(1)

where \(\hat{\mathcal {L}}^{t}_{\text {Proxy}}(\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}) \overset{\scriptscriptstyle \wedge }{=}\frac{1}{M} \sum _{i=1}^{M} \mathcal {L}^{t}_{\text {Proxy}}\left( f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}}^{t}(\boldsymbol{x}_{i}), y_{i}^{t}\right) \) is the task-specific empirical risk estimated on the training data. For the specific example of SP construction [22], we have to consider three distinct tasks (Fig. 1).

  1. 1.

    (t = 1): Keypoint detection of the posterior Blumensaat line point \(k_{\text {blum}}\) and turning point on the medial femur condyle \(k_{\text {tmc}}\). Both points are encoded as heatmaps sampled from a bivariate Gaussian function with mean at the point coordinates and standard deviation of \(\sigma _{\text {hm}}=6\,\textrm{px}\). The correspondence between the predicted heatmap \(\hat{y}\) and ground truth heatmap \(y\) is optimized using pixel-wise mean squared error (MSE) loss function given by \(\text {MSE}(\hat{y},y)=\mathop {\mathbb {E}}{||\hat{y}-y}||^2_2\). Consequently, \(\mathcal {L}^{1}_{\text {Proxy}}:=\text {MSE}(\hat{y}^{1}_{i},y^{1}_{i})\).

  2. 2.

    (t = 2): Line regression of the tangent to the posterior femur shaft cortex \(\textbf{l}_{\text {ctx}}\). The line is encoded as a heatmap, where the intensities are computed by evaluating the point-to-line distances with a Gaussian function with \(\sigma _{\text {hm}}=6\,\textrm{px}\) [11, 13]. Similarly, \(\mathcal {L}^{2}_{\text {Proxy}}:=\text {MSE}(\hat{y}^{2}_{i}, y^{2}_{i})\).

  3. 3.

    (t = 3): Semantic segmentation of the femur region \(S\). As described in [11], \(S\) can be combined with the line heatmap to mask the relevant section \(C^{\prime }\subseteq {C}\) of segmentation contour \(C\subseteq {S}\) for more precise positioning and angulation in the subsequent major axis regression [26] of relevant line points. For the loss function, we use a pixel-wise binary cross entropy (BCE) given by \(\text {BCE}(\hat{y},y):=- \left[ y\log (\sigma (\hat{y}))+(1-y)\log (1-\sigma (\hat{y})) \right] \) with sigmoid nonlinearity \(\sigma \). Consequently, \(\mathcal {L}^{3}_{\text {Proxy}}:=\text {BCE}(\hat{y}^3_i,y^3_i)\).

After extracting the relevant features, they are converted to geometric primitives and interrelated according to the planning geometry (Fig. 1-2). This geometry describes consecutive calculations to localize the planning target relevant to the surgeon. For MPFL planning, the cortex tangent line is determined by major axis regression [26] on relevant contour points. The SP can be approximated by the center of the inscribed circle bounded by the tangent and two orthogonal lines intersecting both detected keypoints (Fig. 1).

2.2 Deep Geometric Supervision (DGS)

The disconnect between the proxy function and the actual planning target limits generalization to unfavorable but common image characteristics. We approach this issue by introducing the concept of Deep Geometric Supervision. To this end, we add a companion objective function to the original ERM term (Eq. 1) that directly minimizes positioning errors of the planning target while retaining the relations of the planning geometry (Fig. 1-3).

Mathematically, we start by combining all geometric steps in a single non-parametric function \(g: \mathcal {Y}^{1}\times \dots \times \mathcal {Y}^{T}\rightarrow \mathcal {P}\) that operates on the outputs of the anatomical feature extractor \(f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}}^{t}\). The output of \(g\) is the desired planning target, e.g., a keypoint. Next, we calculate the positioning error of the planning target with the loss function \(\mathcal {L}_{\text {DGS}}(\cdot ,\cdot ):\mathcal {P}\times \mathcal {P}\rightarrow \mathbb {R}^{+}_{0}\). The empirical risk is given by \(\hat{\mathcal {L}}_{\text {DGS}}(\boldsymbol{\theta }^{sh},\boldsymbol{\theta }^{1}, \ldots , \boldsymbol{\theta }^{T}) \overset{\scriptscriptstyle \wedge }{=}\frac{1}{M} \sum _{i=1}^{M} \mathcal {L}_{\text {DGS}}\left( g\left( f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{1}}^{1}(\boldsymbol{x}_{i}), \dots , f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{T}}^{T}(\boldsymbol{x}_{i})\right) , p_{i}\right) \).

Finally, adding this term to the original ERM formulation yields

(2)

where \(\lambda \in \mathbb {R}\) is a multiplicative risk-weighting term. Here, \(\mathcal {L}_{\text {DGS}}:=||\hat{p}_{i} - p_{i}||_2\). Since the planning function \(g\) is not subject to trainable parameters, the minimization of the additional risk term \(\hat{\mathcal {L}}_{\text {DGS}}\) should directly contribute to updates of \(\boldsymbol{\theta }^{sh} \) and \(\boldsymbol{\theta }^{t}\). For that purpose, \((g\circ f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}}^{t})\) must be a continuously differentiable function, such that \((g\circ f_{\boldsymbol{\theta }^{sh}, \boldsymbol{\theta }^{t}}^{t}) \in C^{1} (\mathcal {X}, \mathcal {P})\). To fulfill this constraint, the representations and objective functions for keypoint and line regression need to be changed from their original formulation in [13]. Matching the keypoint heatmaps with MSE is not feasible as it is typically followed by a subsequent non-differentiable argmax operation to extract the intensity peak’s \(x\) and \(y\) coordinates. We instead use the regularized spatial-to-numerical transform (DSNT) [18]. For that purpose, the predicted heatmap \(\hat{y}\) is rectified applying a spatial softmax and normalized with the L1 norm. The result of this standardization \(\hat{y}^{\prime }\) is transformed to the numerical coordinate \(\hat{c}=\text {DSNT}(\hat{y}^{\prime })\) in the range of \([-1, 1]\) exploiting a probabilistic interpretation of \(\hat{y}^{\prime }\). This allows the cost function to operate directly on numerical coordinates and optimize the heatmaps implicitly. Finally, the keypoint loss function is updated to \(\mathcal {L}^{1}_{\text {Proxy}}:=||\hat{c}^{1}_{i}-c^{1}_{i}||_2+D_{\text {JS}}\big ( p(\hat{y}^{1}_{i})\,\Vert \, \mathcal {N}(y^{1}_{i}, \sigma ^{2}_{\text {hm}} I_2) \big )\). \(p(\cdot )\) is a probability mass function under the interpretation of the predicted coordinates as discrete bivariate random vectors, and \(D_{\text {JS}}(\cdot \Vert \cdot )\) is the Jensen-Shannon divergence which encourages similarity of the heatmaps to a Gaussian prior [18].

A differentiable representation of the line’s position and orientation is obtained by calculating raw image moments \(M_{pq}\) and second order central moments \(\mu _{pq}^{\prime }\) on the line heatmap [7, 20]. The centroid \(c_{x,y}\) and orientation angle \(\gamma \) are given by \(c_{x,y}=\left( M_{10}/M_{00},M_{01}/M_{00}\right) \) and \(\gamma ={\frac{1}{2}}\arctan \left( 2\mu _{11}^{\prime }/(\mu _{20}^{\prime }-\mu _{02}^{\prime })\right) + \frac{\pi }{2} \left[ \mu _{20}^{\prime }<\mu _{02}^{\prime }\right] \). \([\cdot ]\) marks the Iverson bracket.

2.3 Model Variants

We define three model variants to evaluate the effect of DGS on planning accuracy and spatial generalization. A) Proxy, which uses all three anatomical detection tasks and uses the original ERM term Eq. 1 without DGS. The planning target is calculated with geometric post-processing. B) Proxy\(-Seg\)+DGS, which utilizes the updated ERM term Eq. 2. Here, \(g\) is used to calculate the planning target, and the segmentation task is omitted. C) Proxy+DGS, which uses ERM term Eq. 2 but keeps the segmentation task to allow direct comparison without the external factor of different task and parameter counts.

2.4 Datasets and Training Protocol

Method evaluation was done on two radiographic image cohorts of the lateral knee joint. Cohort 1) contains 221 diagnostic radiographs collected retrospectively from anonymized databases. For each image, the SP geometry was annotated by an expert trauma surgeon with a proprietary tool by Siemens Healthcare GmbH. The femur polygon was labeled by a medical engineer using labelme software [25]. The images were split into three sets for training (167), validation (16), and testing (38) with stratified sampling [10]. There, all data showing a steel sphere of 30 mm diameter was assigned to the test split, allowing conversion from pixel to mm space. Cohort 2) contains 89 intra-operative X-ray images from 43 patients acquired with mobile C-arm systems. Most images show severely truncated bone shafts and instrumented anatomy. The images were annotated by a medical engineer using a custom extension of labelme [25]. The data was divided into training (61), validation (9), and test (19) with no patient overlap. During optimization, the training data was augmented using horizontal flipping (\(p=0.5\)), rotation (\(\alpha \in [-45^{\circ }, 45^{\circ }]\), \(p=1\)), and scaling (\(s\in [0.8, 1.2]\), \(p=1\)) [13]. After min-max normalization of the images to the intensity range of \([0,1]\), the data were standardized to the dimensions \([\text {H:}256 \times \text {W:}256]\,\textrm{px}\) by bi-cubic sampling and zero-padding to preserve the original aspect ratios. For each cohort and variant, an MTL hourglass network [13, 17] (128 feature root) was trained for 450 epochs using an Adam optimizer, a learning rate of 0.001/0.0006 (cohort 1/2), a batch size of 2, and multiplicative learning rate decay of 0.1 after 350 epochs. The risk-weighting with \(\lambda =0.99\) was re-balanced [9] by decreasing \(\lambda \in [0.01,0.99]\) by 0.01 every forth epoch. Implementation was done in PyTorch v1.8 [19] (Python v3.8.12, CUDA v11.0) and reproducibility was confirmed.

3 Results

Effects on Feature Extraction and Positioning Accuracy (RQ 1). The results of model evaluation on Cohort 1) are summarized in Fig. 2. DGS reduces the median SP Euclidean Distance (ED) error from \(2.29\,[1.84, 2.82]_{\text {CI}95}\,\textrm{mm}\) (A) to \(1.68\,[1.19, 2.17]_{\text {CI}95}\,\textrm{mm}\) (B) and \(1.58\,[1.15 2.09]_{\text {CI}95}\,\textrm{mm}\) (C), respectively (Fig. 2-a). Between the two DGS variants, we observe no drop in performance when additionally solving the segmentation task. This understanding lets us reject insufficient model capacity or conflicting task configurations as a reason for inferior performance of the proxy optimization. Furthermore, DGS increases the number of predictions that fall within the clinically relevant precision range of \(2.5\,\textrm{mm}\) [22] from \(63.2\%\) (Model A) to \(76.3\%\) (Model B &C) (Fig. 2-b). Interestingly, DGS slightly changes the spatial appearance of the line heatmaps, increasing activations in the posterior aspect of the Blumensaat line (Fig. 2-c). Since this area resides on the tangential extension of the shaft cortex, we argue that activation in this region allows to compensate for small errors in line alignment.

Fig. 2.
figure 2

Summary of model evaluation on Cohort 1). a, violin plots of the positioning errors on the test set (ED: Euclidean Distance; white dots mark individual planning samples). Statistical significance was evaluated with a two-sided Mann-Whitney U rank test. b, error distribution w.r.t. clinically relevant precision ranges. c, planning geometry (red: prediction, green: ground truth) and spatial appearance of line heatmaps. (Color figure online)

Full size image

Effects on Spatial Generalization (RQ2). To evaluate potential effects of DGS on spatial generalization, we constructed a secondary test set with different levels of shaft truncation. For this purpose, multiple crops per image were created such that the visible bone shaft corresponds to a fixed ratio \(t\in [0.8, 2.7]\) between bone axis length and femur head width. The results are summarized in Fig. 3. We see considerable improvements for severely truncated shafts for both variants with DGS. This observation is underlined by a strong Spearman’s rank correlation of \(r_s={-0.79}\) for Model A compared to moderate correlations of \(r_s={-0.48}\) and \(r_s={-0.53}\) for the DGS Models B and C, respectively (\(p\ll 0.01\) for all correlations). Visual inspection shows that the tangent determined via the bone contour experiences a systematic angular offset in the postero-distal direction for very short shaft lengths. Optimization with DGS can recover the optimal tangent direction in most of these cases despite insufficient image information.

Fig. 3.
figure 3

Dependencies of the model variants to different levels of bone shaft truncation.

Full size image
Fig. 4.
figure 4

Evaluation on Cohort 2). a, test set positioning errors. b, relevant precision classes. c, planning geometry (red: prediction, green: ground truth) and line heatmaps. (Color figure online)

Full size image

Application to Complex Intra-Operative Data (RQ 3). The evaluation on the intra-operative Cohort 2) is summarized in Fig. 4. Similar to Cohort 1), DGS reduces the positioning error significantly, yielding median ED scores of \(3.50\,[2.47, 6.92]_{\text {CI}95}\,\textrm{px}\) and \(3.44\,[2.09, 6.67]_{\text {CI}95}\,\textrm{px}\) for Model A and B, respectively. The improvements over the original proxy formulation with a median error of \(8.70\,[5.06, 16.60]_{\text {CI}95}\,\textrm{px}\) can be explained by generally shorter shaft lengths caused by a smaller field of view of the mobile C-arm imaging device and less standardized acquisition. As seen before, this characteristic leads to misaligned tangent predictions during proxy optimization. The compensation effect previously identified in the DGS variants, which is characterized by additional activation peaks in the distal region of the femur, is clearly enhanced (Fig. 4-c).

4 Discussion

Directly optimizing the planning target position while preserving the geometric relation of the anatomical structures promises a more precise, better generalizing, and clinically motivated planning automation in orthopedics. To accommodate this rationale, we developed and analyzed the concept of Deep Geometric Supervision. By interpreting the planning geometry as a differentiable function, the planning target and the anatomical feature extractor can be optimized jointly. Improving target positioning accuracy while maintaining the core idea of step-wise geometric planning is a critical design decision that fosters clinical acceptance. Intriguingly, integrating the planning function into the computation graph can be interpreted as learning with a known operator [16], allowing end-to-end training and effectively reducing the upper error bound. In this context, it should be noted that minimizing only the DGS term yields a trivial solution where the extracted landmarks collapse to a single point at the planning target position. While these solutions offer competitive precision, they are undesirable because they do not mimic the clinically established planning workflow and cannot be easily verified for anatomic fidelity. An important trait of DGS is the improvement in spatial generalization. Especially in the intra-operative environment with constrained patient and device positioning, we cannot always expect standard acquisitions with sufficiently large bone shafts. There, DGS successfully bridges the semantic gaps present in the current proxy optimization strategy, reducing malpositioning when landmark visibility is limited. Besides these advantages, our current implementation of the planning function imposes little geometric constraints and, in theory, allows for different anatomical feature configurations that arrive at the same planning target. Reducing the space of possible solutions could ensure planning fidelity and smooth the optimization landscape.

Despite this limitation, our method effectively improves positioning accuracy and spatial generalization in orthopedic surgical planning. At the same time, it allows maintaining the clinically established planning geometry. We believe that these aspects facilitate the translation of planning automation concepts to the field and will ultimately motivate the development of new planning guidelines.