Keywords

1 Introduction

Deep learning-based methods have made great progress in the field of medical imaging [4,5,6,7]. Although they have achieved superior performance over traditional methods, the reliability of deep learning-based methods has always been questioned as they are data-driven models and work in a black box. Once the testing data is out of the distribution of the training data, the output would be degraded. Therefore, quantifying uncertainty during the inference of deep learning-based methods is of vital importance. Especially in clinical practice, uncertain information can effectively improve the accuracy of diagnosis. Thiagarajan et al. [27] measured uncertainty for the classification of breast histopathological images and verified that high uncertainty data have lower classification accuracy and need human intervention. Hao et al. [11] showed that adding uncertainty information into a graph attention network can improve the classification performance for parapneumonic effusion diagnosis.

In positron emission tomography (PET) image denoising tasks, without prior information from raw data, it is not easy for denoising models to distinguish noise and small tumors as they have very similar structures visually. Small tumors may be eliminated as noise, while some of the noise may be identified as a tumor and retained. If we can quantify the uncertainty for the denoising process, the uncertainty map can provide an additional reference when the radiologists are viewing the denoised PET imaging. Uncertainty has been well studied in the classic PET literature, particularly after Jeffrey Fessler’s seminar work [9] in 1997. However, traditional methods [9, 21] are not accurate and fast enough. Nowadays, several deep learning-based methods for uncertainty estimation have been proposed, like Bayesian neural networks [18, 19, 24, 26], ensemble methods [17], dropout methods [2, 10], and uncertainty aware neural networks [3, 20]. For PET image denoising, Sudarshan et al. [26] proposed a robust suDNN to map low-dose PET images to standard-dose PET images and estimate the uncertainty through a Bayesian neural network framework. Cui et al. [8] used a novel neural network, Nouveau variational autoencoder (NVAE) [28], to generate denoising image and uncertainty map based on Monte Carlo sampling.

In this paper, we developed an efficient and effective model for simultaneous PET image denoising and uncertainty estimation. Here, we also utilized NVAE as our network structure due to its superior performance over the traditional VAE model. Compared to the Reference [8], our work has two main contributions:

  • Quantile regression loss [1, 13, 16] was introduced as the reconstruction loss to avoid the variance shrinkage problem of VAE. In VAE, when the conditional mean network prediction is well-trained (there is no reconstruction error), continued maximizing the log-likelihood will result in the estimated variance approaching zero [1], leading to an artificially narrow output distribution. This will limit the model’s generalization ability and reduce sample diversity. Using quantile regression loss to replace log-likelihood can avoid this problem.

  • The variance map was directly calculated from the estimated quantiles. Monte Carlo sampling is no longer needed which can save a lot of time and computing resources.

2 Related Work

2.1 Variational Autoencoder (VAE)

VAE [14] is a generative model that is trained to represent the distribution of signal \(\boldsymbol{x}\) given the latent variables \(\boldsymbol{z}\) which has a known prior distribution \(p(\boldsymbol{z})\). \(p(\boldsymbol{x},\boldsymbol{z})=p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z})\) represents the true joint distribution of \(\boldsymbol{x}\) and \(\boldsymbol{z}\), where \(p(\boldsymbol{x}|\boldsymbol{z})\) is the likelihood function or decoder. Let \(q(\boldsymbol{x})\) be the distribution of \(\boldsymbol{x}\) and \(q(\boldsymbol{z}|\boldsymbol{x})\) be the posterior distribution or encoder, then \(q(\boldsymbol{x},\boldsymbol{z})\) suppose be the estimate of \(p(\boldsymbol{x},\boldsymbol{z})\). VAE is trained to make \(q(\boldsymbol{x},\boldsymbol{z})\) close to the true joint distribution \(p(\boldsymbol{x},\boldsymbol{z})\) by minimizing their KL divergence.

2.2 Nouveau Variational Autoencoder (NVAE)

NVAE [28] is a model recently proposed by NVIDA that can generate high-quality face images as large as \(256\times 256\). Through several novel architecture designs, NVAE greatly improved its generative performance for complex signal distribution. A hierarchical multi-scale structure is added between the encoder and the generative model to boost the expressiveness of the approximate posterior \(q(\boldsymbol{z}|\boldsymbol{x})\) and prior \(p(\boldsymbol{z})\). In this hierarchical multi-scale structure, the latent variables of NVAE are separated as L disjoint groups, \({\boldsymbol{z}} = \left\{ {{\boldsymbol{z}_1},{\boldsymbol{z}_2}, \ldots ,{\boldsymbol{z}_L}} \right\} \). Thus, the posterior can be represented as \(p({\boldsymbol{z}_1},{\boldsymbol{z}_2}, \ldots ,{\boldsymbol{z}_L}) = p({\boldsymbol{z}_1})\prod \nolimits _{l = 1}^L {p\left( {{\boldsymbol{z}_i}|{\boldsymbol{z}_{ < l}}} \right) } \) and the prior is \(q({\boldsymbol{z}_1},{\boldsymbol{z}_2}, \ldots ,{\boldsymbol{z}_L}|\boldsymbol{x}) = \prod \nolimits _{l = 1}^L {q\left( {{\boldsymbol{z}_l}|\boldsymbol{x},{\boldsymbol{z}_{ < l}}} \right) } \). Considering the substantial latent variable groups would make the network hard to optimize and unstable, NVAE proposed the residual normal distributions to parameterize the approximate posterior \({{q(z}}_l^i|{\boldsymbol{z}_{< l}},\boldsymbol{x}): = { \mathcal {N}}({\mu _i}\left( {\boldsymbol{z}_{< l}} \right) + \varDelta {\mu _i}\left( {\boldsymbol{z}_{< l},\boldsymbol{x}} \right) ,{\sigma _i} \left( {\boldsymbol{z}_{< l}} \right) \cdot \varDelta {\sigma _i}\left( {\boldsymbol{z}_{ < l},\boldsymbol{x}} \right) )\) relative to the prior \({{p(z}}_l^i|{\boldsymbol{z}_{< l}}): = { \mathcal {N}}({\mu _i}\left( {{\boldsymbol{z}_{< l}}} \right) ,{\sigma _i}\left( {{\boldsymbol{z}_{ < l}}} \right) )\), where \(z_l^i\) is the ith variable in \(\boldsymbol{z}_l\). In addition, spectral regularization [30], inverse autoregressive flow [15], depthwise convolutions, squeeze and excitation [12], batch normalization, swish activation [22] were added either to better model the long-range correlations or stable the training.

3 Methods

3.1 Overview

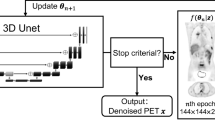
Figure 1 shows the diagram of the proposed simultaneous PET image denoising and uncertainty estimation framework. The NVAE network was trained with supervision by minimizing quantile regression loss and Kullback-Leibler (KL) divergence term. The posterior distribution was assumed to be the Logistic distribution. After training, the location parameter \(\mu \) and the scale parameter s were acquired from the estimated quantiles. Thus, the mean and variance of the Logistic distribution can be calculated.

Fig. 1.
figure 1

Diagram of the proposed framework.

Full size image

3.2 PET Image Denoising

For PET image denoising tasks, given a group of noisy PET images \(\boldsymbol{x}'\) and clean PET images \(\boldsymbol{x}\), the conditional log-likelihood function is \(\log p(\boldsymbol{x}|\boldsymbol{x}')\). Based on the conditional VAE [25], the variational lower bound of the log-likelihood can be written as:

$$\begin{aligned} \log p(\boldsymbol{x}'|\boldsymbol{x}) \ge {{\mathbb {E}}_{q({\boldsymbol{z}}|\boldsymbol{x}')}}\log p(\boldsymbol{x}|\boldsymbol{x}',\boldsymbol{z}) - KL(q(\boldsymbol{z}|\boldsymbol{x}')||p(\boldsymbol{z}|\boldsymbol{x}')). \end{aligned}$$
(1)

In this work, we assumed \(p(\boldsymbol{z}|\boldsymbol{x}')=p(\boldsymbol{z})\) that followed Normal distributions. And skip connections were added between the encoder and the generative model to provide information from input \(\boldsymbol{x}'\) to the likelihood function \(p(\boldsymbol{x}|\boldsymbol{x}',\boldsymbol{z})\). Thus, the loss can be written as:

$$\begin{aligned} \mathcal {L}(\boldsymbol{x})=-{{\mathbb {E}}_{q({\boldsymbol{z}}|\boldsymbol{x}')}}\log p(\boldsymbol{x}|\boldsymbol{x}',\boldsymbol{z}) + KL(q(\boldsymbol{z}|\boldsymbol{x}')||p(\boldsymbol{z})). \end{aligned}$$
(2)

The first term of the Eq. 2 represents the reconstruction loss \(\mathcal {L}_{REC}(\boldsymbol{x})\) and the second term is the regularization term \(\mathcal {L}_{KL}(\boldsymbol{x})\).

3.3 Quantile Regression Loss

Quantile regression (QR) [16] was proposed by Koenker et al. in 1978, which estimates the nth \((0<n<1)\) quantile \(Q_n\) by minimizing the problem

$$\begin{aligned} \mathop {\min }\limits _\theta \sum \limits _t {{\rho _n}\left( {{x_t} - {f_\theta }({x'_t})} \right) }, \end{aligned}$$
(3)

where \(x'_t\) and \(x_t\) are the tth input and response, respectively. \({f_\theta }({x'_t})\) represents the NVAE model with parameters \(\theta \), which is supposed to be the quantile \(Q_n\) after optimizing. \({\rho _n}\) is the check function:

$$\begin{aligned} {\rho _n}(u) = u(nI(u > 0) - (1 - n)I(u < 0)). \end{aligned}$$
(4)

To avoid the variance shrinkage problem, we replaced the reconstruction loss with the quantile regression loss and calculated the mean and variance of the output distribution by quantiles. We assumed that the output distribution follows the Logistic distribution, which has a cumulative distribution function (CDF) as:

$$\begin{aligned} F(y;\mu ,s) = \frac{1}{{1 + {e^{ - (y - \mu )/s}}}} \end{aligned}$$
(5)

where \(\mu \) is the mean and s is a scale parameter. s has a relation with the variance as \({\sigma }^2 = \frac{{{s^2}{\pi ^2}}}{3}\). As CDF is equal to n, we can get two quantiles:

$$\begin{aligned} {Q_n} = \left\{ {\begin{array}{*{20}{c}} {\mu ,n = 0.5}\\ {\mu - s,n = \frac{1}{{1 + e}} \approx 0.269} \end{array}} \right. \end{aligned}$$
(6)

The QR loss aims to estimate the 0.5th quantile and the 0.269th quantile by:

$$\begin{aligned} \mathcal {L}_{QR}(\boldsymbol{x}) = \sum \limits _t {{\rho _{0.5}}\left( {{x_t} - {f_{{\theta _{0.5}}}}({{x'}_t})} \right) } + \sum \limits _t {{\rho _{0.269}}\left( {{x_t} - {f_{{\theta _{0.269}}}}({{x'}_t})} \right) } \end{aligned}$$
(7)

Thus, the total training loss for the proposed work is

$$\begin{aligned} \mathcal {L}(\boldsymbol{x})=\mathcal {L}_{QR}(\boldsymbol{x})+\mathcal {L}_{KL}(\boldsymbol{x}). \end{aligned}$$
(8)

4 Experiment

4.1 Dataset

The proposed method was validated on real \(^{11}\)C-DASB datasets, which contain 26 subjects. Each subject was scanned by the HRRT-PET system (Siemens Medical Solutions, Knoxville, TN, USA) with the administered dose of 577.6 ± 41.0 MBq. PET images acquired at 60 min post-injection (matrix size, \(256 \times 256 \times 207\); voxel size, \(1.21875\,\textrm{mm} \times 1.21875\,\textrm{mm} \times 1.21875\,\textrm{mm}\)) were reconstructed by 3D-ordinary ordered subset expectation maximization (OP-OSEM3D) algorithm and attenuation correction was performed. Each subject also has a T1-weighted image scanned by an ultra-high field 7T MRI. We generated the low-quality PET images by down-sampling the list-mode data to a quarter of the original count. In this dataset, 20 subjects were used for training, 3 for validation, and 3 for testing.

4.2 Data Analysis

Supervised denoising using Unet as the network structure was chosen as the baseline to compare the denoising performance with the proposed method (NVAE-QR). We also compared with the work in the Reference [8], which used NVAE for PET image denoising and uncertainty estimation based on Monte Carlo sampling (NVAE-MC). In this work, we evaluated the denoising performance by calculating the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) [29] using the high-quality PET image as the reference. We used Logistic distribution as the output distribution for NVAE-QR. NVAE-MC used the mixture of discretized Logistic distribution [23] as the output distribution.

The network was trained by 2.5D patch with the size of \(3 \times 256 \times 256\). The batch size is 20. The training epochs are 200 and the learning rate is 0.01. All the experiments were performed in Pytorch 1.9.1. The sampling number for NVAE-MC is 500.

Table 1. The PSNR and SSIM of the noisy PET image, the denoising results for Unet, NVAE-MC and NVAE-QR.
Full size table
Fig. 2.
figure 2

The output of our NVAE-QR methods. From left to right: the estimated 0.269th quantile, the estimated 0.5th quantile, the scale parameter s and the variance calculated based on s. The color bar shows the normalized intensity value. (Color figure online)

Full size image

5 Results

Figure 2 shows one axial slice from the output of our NVAE-QR methods. The network directly estimated the 0.5th quantile and the 0.269th quantile, which are equal to \(\mu \) and \(\mu -s\), respectively. We can get the scale parameter s from the difference image of the 0.5th quantile and the 0.269th quantile, and then calculate the variance image. Figure 3 displays the denoising results for Unet, NVAE-MC, and NVAE-QR. We can see that all the neural network denoised results significantly improved the quality of the low-dose image and even look better than the full-dose image. Among them, our NVAE-QR shows the clearest cortex structure (as the zoom-in subfigures are shown). As \(^{11}\)C has a short half-life and decays fast, \(^{11}\)C-DASB PET images usually have a higher noise level compared to \(^{18}\)F-FDG. Thus, the full-dose PET image shown in Fig. 3 is also noisy and cannot give enough reference for cortex regions. The corresponding MR is displayed to provide additional references. We also plotted the profile of the denoised results using different methods in Fig. 4. We can see that NVAE-QR matches the high-intensity peak better than the other two methods. The PSNR and SSIM of different denoising methods are listed in Table 1. The proposed NVAE-QR method can achieve the highest mean(±SD) PSNR (40.64 ± 5.71) and SSIM (0.9807 ± 0.0063) compared to Unet (PSNR, 36.18 ± 5.55; SSIM, 0.9614 ± 0.0121) and NVAE-MC (PSNR, 37.00 ± 5.35; SSIM, 0.9671 ± 0.0095). The variance maps of NVAE-MC and NVAE-QR are shown in Fig. 5. The variance of NVAE-MC is lower than NVAE-QR due to the variance shrinkage problem. We also compared the performance of NVAE-MC using Logistic distribution and NVAE-QR using Normal distribution as the ablation study. The PSNR and SSIM in Table 2 show that NVAE-QR using Logistic distribution has the best performance.

Fig. 3.
figure 3

The denoising results of different methods. From left to right: corresponding MR image, full-dose PET image, low-dose PET image, the denoised image using Unet, NVAE-MC and NVAE-QR. The region in the red box was zoomed-in for each image. The color bar shows the normalized intensity value. (Color figure online)

Full size image
Fig. 4.
figure 4

The profile of the black line for full-dose PET image, the denoised image using Unet, NVAE-MC and NVAE-QR.

Full size image

6 Discussion

In this work, we used quantile regression loss to replace the original reconstruction probability loss of the NAVE model to avoid the variance shrinkage problem [1]. The mean value of the variance map of NVAE-QR is 0.00142 which is 1.58 times of NVAE-MC (0.000898), showing that NVAR-QR does avoid variance shrinkage. From Table 2 we can see that using quantile regression can significantly improve the PSNR and SSIM for the denoised images.

In addition to superior denoising capability, another advantage for NVAE-QR is that it can save a lot of sampling time. NVAE-MC needed 35min to generate the result of one subject due to the repetitive sampling process, while NVAE-QR only needed 4s. There is not much difference between 1-sample and 500-sample NVAE-QR results. (The comparison is put in the supplementary materials). Thus, NVAE-QR only takes 1/500 percent of the time of NVAE-MC, which is much more efficient.

Fig. 5.
figure 5

The denoising PET image and variance map of NVAE-MC and NVAE-QR using different output distributions. From left to right: full-dose PET image, NVAE-MC based on the Logistic distribution, NVAE-MC based on the mixture of Logistic distribution, NVAE-QR based on the Normal distribution, and NVAE-QR based on the Logistic distribution. The color bar shows the normalized intensity value. (Color figure online)

Full size image
Table 2. The PSNR and SSIM of NVAE-MC and NVAE-QR using different output distributions
Full size table

We evaluated the performance of different output distribution models (as Fig. 5 and Table 2 are shown). We found that normal distribution cannot fit PET data well (usually has low SSIM). Both logistic and the mixture of discretized Logistic distribution [23] work well. However, the mean and variance of the mixture of discretized Logistic distribution [23] are hard to calculate as the mixture parameters are learned by the network. Thus, we assumed that the output follows the logistic distribution. We also evaluated the proposed method on whole-body \(^{18}\)F-FDG datasets. The results show that NVAE-QR achieved the highest PSNR, SSIM, and contrast-to-noise ratio (CNR) improvement than Unet and NVAE-MC. The results of the brain datasets and the whole-body datasets show our model works well under this output assumption and has good generalization ability.

7 Conclusion

In this paper, we proposed an NVAE model using quantile regression loss for simultaneous PET denoising and uncertainty estimation. Based on the quantile regression loss, the variance shrinkage problem caused by reconstruction probability loss can be avoided and the sampling time can be saved. The experiment based on real \(^{11}\)C-DASB HRRT-PET dataset verified that the proposed NVAE-QR method outperforms the Unet-based denoising and NVAE-based Monte Carlo sampling. Our future work will focus on more clinical evaluations.