Liquid State Machine on Loihi: Memory Metric for Performance Prediction

Abstract

Liquid State Machine (LSM) is a spiking variant of recurrent neural networks with promising results for speech, video and other temporal datasets classification. LSM employ a network of fixed and randomly connected neurons, called a reservoir. Parameter selection for building the best performing reservoir is a difficult task given the vast parameter space. A memory metric extracted from a state-space approximation of the LSM has been proposed in the past and empirically shown to be best-in-class for performance prediction. However, the working principle of this memory metric has not been studied. We first show equivalence of LSM simulated on MATLAB to those run on Intel’s neuromorphic chip Loihi. This enables us to perform in-depth statistical analysis of the memory metric on Loihi: effect of weight scaling and effect of time averaging window. Analysis of state space matrices generated with a reasonably sized averaging window reveal that the diagonal elements are sufficient to capture network dynamics. This strengthens the relevance of the first order decay constant based memory metric which correlates well with the classification performance.

1 Introduction

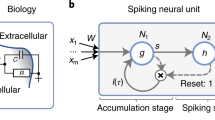
Liquid State Machines (LSM) are Spiking Neural Networks (SNNs), which come under the field of reservoir computing. It consists of a reservoir of neurons recurrently connected randomly with random non-plastic synapses followed by a discriminator layer (Fig. 1 (a)). The reservoir is able to project input times series data into a hyperdimensional space which can be clustered and classified by the discriminator layer more effectively [10]. A major advantage of LSMs is that the plastic synapses are limited to the discriminator layer while the reservoir consists of non-plastic synapses, reducing the total training burden [7]. LSM has shown state-of-the-art results for classification of various time series [1, 3, 13], speech [15, 16], video [14] datasets, and reinforcement learning [12].

One of the main challenges of using LSM for different tasks is tuning the reservoir such that it produces the best classification performance. Performance prediction metrics alleviate this problem as they can be derived from the reservoir dynamics alone without the need for elaborate training and testing. Kernel quality [8], class separation [11] and Lyapunov exponent [5] are some of such metrics. They are based on the separation property of the reservoir i.e. ability to separate two close inputs. Lyapunov exponent, a measure of chaotic behavior of a network, long outperformed other metrics mentioned by showing best correlation with performance and identifying edge of chaos operation [2]. In contrast, the memory metric ($\tau _M$) proposed by Gorad et al. [6] is based on a linear state-space mapping of LSM (Fig. 1(b)) which estimates the extent that past excitation predicts the future linearly to embody the “memory” of the network. Memory metric has empirically outperformed Lyapunov exponent making a strong case of it being the preferred metric for performance prediction.

However, the working principle of the memory metric estimation requires further examination. In order to perform in-depth statistical analysis to answer these questions, we first demonstrate equivalence of networks run on Intel’s neuromorphic chip Loihi to MATLAB simulations. Equipped with the power and time efficiency of Loihi, the following questions need to be addressed: (1) Why does a metric based purely on self-excitation (diagonal) terms [6] while ignoring the cross-excitation (non-diagonal) terms of the reservoir’s state space matrix precisely predict the performance? (2) What is the role of the averaging time window size used to extract the state space matrices and subsequently the memory metric? A comparison and focus of our work with other relevant works is summarised in Table 1.

Fig. 1.

(a) Liquid State Machine schematic, (b) Corresponding state-space approximation of LSM

Table 1. Contribution of this work vis a vis state-of-the-art

2 Background on Performance Metrics

2.1 Lyapunov Exponent

Lyapunov exponent ($\mu$) has long been used in characterizing the separation of two close trajectories in dynamical systems. For LSMs, the metric characterizes the rate of separation in activity of reservoir generated by two nearly identical inputs [5]. Edge-of-chaos state of reservoir associated with high performance [8] is based on Lyapunov exponent approaching unity. For inputs $u_i$ and $u_j$ and their reservoir responses $x_i$ and $x_j$, $\mu (t)$ is defined as:

$$\begin{aligned} \mu (t) = ln\frac{||x_i(t)-x_j(t)||}{||u_i(t)-u_j(t)||} \end{aligned}$$

(1)

2.2 Memory Metric

State-space representation is widely used for modeling linear systems. Interestingly, it is used to model non-linear dynamics of LSM in [6]. Spike rates obtained by averaging over moving time window are used to model the state-space approximation for the reservoir (Fig. 1(b)):

$$\begin{aligned} X^{k+1} = A X^k + B U^k \end{aligned}$$

(2)

$X^k$ and $U^k$ are reservoir and input signal spike rates respectively at time instant k and A and B are constant matrices. Matrices A and B can be obtained using actual spike rate X and input U as follows:

$$\begin{aligned} X_{+1} = [A | B]_1 [X | U]_0 \end{aligned}$$

(3)

$$\begin{aligned}{}[A | B]_1 = X_{+1} pinv([X | U]_0) \end{aligned}$$

(4)

$X_{+1}$ is one time step shifted version of X. pinv is the Moore-Penrose inverse and $[A | B]_i$ represents the concatenation of matrices A and B in dimension i. The memory of N dimensional state space (Eq. 5) with N time constants is defined using Eq. 6. diag(a, b, c) indicates a diagonal matrix with a, b and c as diagonal elements.

$$\begin{aligned} \dot{X}= - diag(\frac{1}{\tau _1},\frac{1}{\tau _2},...,\frac{1}{\tau _N})X \end{aligned}$$

(5)

$$\begin{aligned} \tau _M=\frac{1}{N}\sum _{i=1}^{N}\tau _i \end{aligned}$$

(6)

For matrix A, the above definition can be used by considering vector a of diagonal elements of A. For discrete system with h as time-step, memory metric $\tau _M$ is:

$$\begin{aligned} \tau _M=\frac{1}{N}\sum _{i=1}^{N}\frac{h}{1-|a_i|} \end{aligned}$$

(7)

Time-step is fixed to 1 ms throughout this work. Thus, the metric provides insight into how the current activity of the reservoir will affect future activity. This has shown very good correlation with performance [6].

3 Loihi vs Matlab

3.1 Neuronal Model Used in Loihi

The basic neural model for Loihi [4] is a variation of the leaky-integrate-and-fire model. Spike train is represented by a sum of Dirac delta functions $\sigma (t) = \sum \delta _k (t - t_k)$, where $t_k$ is the time of the k-th spike. The synaptic response current $u_i(t)$ is:

$$\begin{aligned} u_i(t) = \sum _{j\ne i } w_{ij}(\alpha _u * \sigma _j) + b_i, \quad \alpha _u(t) = \frac{1}{\tau _u} e^{(-t/\tau _u)}H(t) \end{aligned}$$

(8)

where $w_{ij}$ is the synaptic weight from neuron j to i, $\alpha _u(t)$ is the synaptic filter impulse response, $\tau _u$ is the time constant and H(t) is a unit step function and $b_i$ is a constant bias current. The membrane potential $v_i(t)$ integrates current, and the neuron sends out a spike when $v_i(t)$ passes its firing threshold $\theta _i$. The neuron remains at resting potential for refractory period $\tau _r$ after it spikes. A discrete and quantized version of these equations is implemented on Loihi and hence need to be validated with ideal MATLAB simulations.

$$\begin{aligned} \dot{v}_i(t) = -\frac{1}{\tau _v}v_i(t) + u_i(t) - \theta _i\sigma _i(t) \end{aligned}$$

(9)

Fig. 2.

Effects of reduced precision on single neuron are shown. One spike is shifted due to error in voltage computation near threshold.

3.2 Neuron Level

A periodic spike train with period of 5 ms is given as an input to a single neuron ($\tau _V$ = 4 ms, $\tau _U$ = 2 ms, $\tau _r$ = 2 ms and $V_{th}$ = 5760 mV). The synapse through which spikes travel to the neuron has weight $w_{in}$ = 55. Figure 2 shows the neuronal voltage, current, and spikes obtained on MATLAB and Loihi for the single neuron case. The mean difference in current was less than 2%. This difference affects neuronal voltage only when it is very close to the threshold.

3.3 Reservoir Level

We create a small reservoir (10 neurons) and a moderate size reservoir (150 neurons) for simulations. Input to reservoir connections are made using bernoulli random variable $p_{in}$. Intra-reservoir connections are chosen randomly with fan out $F_{res}$ fixed. All parameter values are mentioned in Table 2.

As the neuron receives input from multiple neurons (Fig. 3(a) and (b)), the arithmetic operations increase, and along with it the error. The error in spike times propagates to other neurons and hence increases with time. This error increases for a reservoir size of 150 neurons (Fig. 3(c)). However, an idea of reservoir level effect is obtained by obtaining total neuronal spikes at each time instant (13.6% deviation) and total spikes for each neuron across simulation time (4.13% deviation). So, the reservoir level activity is not as badly affected as individual neuronal spike times (Fig. 3(d)).

Table 2. Parameters for 10 and 150 neurons reservoir

Table 3. Reservoir parameter for T1-46 task

3.4 TI-46 Spoken Digit Recognition

We use TI-46 spoken digits dataset for comparing the performance of Loihi and MATLAB. The dataset used contains 500 spoken digits (0–9) utterances from 5 speakers. The inputs are converted to spikes using Lyon auditory cochlear model [9]. Parameters are used from setup in [6]. The output of the pre-processing block is 77 spike trains per input. A reservoir of 125 neurons (5 $\times$ 5 $\times$ 5 grid) is used. The connection topology is based on lambda model where two neurons a and b are connected with probability:

$$\begin{aligned} P(a,b)=K\cdot e^{\frac{-d^2(a,b)}{\lambda ^2}} \end{aligned}$$

(10)

where $\lambda$ is effective connectivity distance and d(a, b) is the euclidean distance. Weights and the constant K depend on kind of pre-synaptic and postsynaptic neuron e.g. $K_{EI}$ for excitatory to inhibitory connection [7]. Parameters for connections and neurons are described in Table 3.

Fig. 3.

Effects of reduced precision for 10 neuron reservoir. Intra-reservoir connections increase (a) voltage error and (b) spike mismatch. Effects of reduced precision for 150 neuron reservoir. (c) Spike event mismatch and (d) Population level mismatch.

The input spikes projected in the high dimensional space of reservoir have to be classified to one of the ten digits. We chose a simple linear classifier (Eq. 11) and minimize the least square loss. $X_s$ contain features from reservoir for given input, $W_{out}$ contains the weights of the classifier and Y is one-hot encoded output. We use total spikes per reservoir neuron across simulation time as our $X_s$ (125-dimensional vector). For training and testing, 5-fold cross-validation is used.

$$\begin{aligned} Y=X_sW_{out} \end{aligned}$$

(11)

It has been shown that effective connectivity distance $\lambda$ and reservoir weight scaling $\alpha _w$ are enough for exploring all major dynamics of a reservoir [7]. We cover the different activity states of a reservoir (no intra-reservoir spike propagation to chaotic). For calculating Lyapunov exponent, $\mu$, we use 2 utterances per digit for a single speaker (20 in total). Time window for getting spike rates for state space approximation is kept at 50 ms. As $\tau _M$ is not based on separation, we use only one utterance per digit by a single speaker (10 in total). Hence, both the metrics require a small fraction of the dataset for predicting performance.

Fig. 4.

(a) $\mu$, error vs. $\alpha _w$ (b) $\tau _M$, error vs. $\alpha _w$. Error rate and behavior of both metrics is similar across platforms. $\tau _M$ peaks in minimum error region while $\mu$ increases monotonically.

Table 4. Performance on T1-46 digit recognition task

Table 5. Correlation of metrics with performance

We were able to run 180 reservoirs in parallel on Loihi (utilizes 18% of neurons on one chip). The test accuracy obtained on both Loihi and MATLAB is close to state-of-the-art models for LSMs of similar reservoir size (Table 4). A slight decrease compared to other works is due to the use of a simpler linear classifier. Memory metric and Lyapunov exponent behavior with varying $\alpha _w$ and corresponding error rate for both platforms are shown in Fig. 4. With variation in $\alpha _w$, a ‘U’ shaped curve for error is obtained. Loihi hardware runs give similar performance. $\tau _M$ peaks in the minimum error region while $\mu$ increases monotonically. This makes $\tau _M$ a better fit for performance prediction. Pearson correlation coefficient (PCC) for $\tau _M$ and error rate is better than the PCC for $\mu$ and error rate in low error regions (Table 5).

4 Analysis of Memory Metric

4.1 Effect of Weight Scaling ($\alpha _w$)

Memory metric only makes use of diagonal elements of matrix A (Eq. 7) which should ideally capture the effect of neuron on itself. Figure 5(a)–(c) shows the reservoir spike rasters for three values of $\alpha _w$ (almost no intra-reservoir connections to highly chaotic and uncorrelated) indicating how recurrent connections within reservoir combine with input spikes to generate reservoir dynamics.

Fig. 5.

Spike rate (window = 50) increases with weight scaling ($\alpha _w$) as intra-reservoir connections increasingly contribute to spikes of connected neurons. Matrix A vs. $\alpha _w$ (d) Very low intra-reservoir spike propagation leads to quick decay of activity along with no activity for many neurons (highlighted in grey dashed boxes and contrasted with (e)). Hence, diagonal elements are on the weaker side. (e) Intra-reservoir connections increases causal activity leading to slower decay of activity and hence stronger diagonal elements. (f) High uncorrelated activity with strong intra-reservoir connections weakens diagonal elements and strengthens non-diagonal elements. (g) Effectiveness of state space model vs $\alpha _w$. Strong dependence on input U gives high PCC for low $\alpha _w$. For high performance regions, high PCC indicates effective modeling. For chaotic state, the state space approximation fails.

Figure 5(d)–(f) shows matrix A for above values of $\alpha _w$ along with extracted $\tau _M$. There is an increase in no. of diagonal elements and memory when going from Fig. 5(d) to Fig. 5(e) followed by sharp decrease in Fig. 5(f). This is associated with increased spike propagation in intra-reservoir connections. One of the reasons that it is reflected in diagonal elements is due to the recurrent connections and averaging window based spike rates being used to model state space. An important aspect of the observed behavior of memory metric is that how well the state space has modeled the actual reservoir spike rate. PCC is calculated for estimated $\hat{X}$ (by using U, A and B) and actual spike rate X. The correlation is very strong in non-chaotic regions as shown in Fig. 5(g).

4.2 Effect of Averaging Window (win)

The length of the moving window used for getting the spike rate plays an important role for a linear state space approximation to non-linear dynamics. Figure 6(a)–(c) shows matrix A for various time windows. For an example spike train in Fig. 6 (d), the ability of different window sizes to capture the temporally varying spike rates is demonstrated. Figure 6 (e) shows PCC for estimated $\hat{X}$ and actual spike rate X along with $\tau _M$ and their variation with window size for the spoken digits reservoir. Hence, a more accurate state space representation (higher PCC) is again correlated with a higher observed memory metric. This behavior is maintained for a decent range of window size.

Fig. 6.

Matrix A vs. window size for the same reservoir. (a) Spike rate changes very fast due to binary nature of spikes which leads to ineffective modeling and hence weak diagonal values. (b) Spike rate change is gradual and effects of gently decaying activity are captured making diagonal values strong. (c) Large window makes spike rate almost constant along with loss of information. (d) An example input spike train and estimated firing rate using windows of size 5, 50 and 500. Small window sizes lead to sharp changes whereas long window sizes lead to smearing out and nearly constant firing rates. An intermediate window size captures the temporally varying firing rate of input spikes. (e) $\tau _M$ and PCC vs. window size for same reservoir. Appropriately large window size is necessary for effective state space modelling and $\tau _M$ is strongly correlated with this effectiveness.

5 Conclusion

Memory Metric has been shown to be the best in-class for performance prediction of LSMs. We establish the equivalence of LSM on Loihi chip with MATLAB simulations. This expands the applicability and robustness of the performance prediction metrics for networks run on accelerated hardware. We show that slowly decaying causal reservoir activity generated through spike propagation from recurrent intra-reservoir connections is captured in the diagonal elements of reservoir state-space matrix. The reservoir is best modelled by state-space when it is around the edge of chaos and appropriate averaging window size is used for spike rates. The extracted memory metric is high both for a well-captured state space approximation and a high network performance. This analysis and generalization of memory metric deems it a very powerful tool for designing and tuning high performing LSMs for very large scale networks.