Keywords

1 Introduction

The acoustic wave propagation and interaction with structures are interesting and challenging engineering field, since a significant part of the research community has been focusing its attention to absorb sound energy, avoid transmission or enhance the sound emissions produced by an object.

Sound absorption is important in many applications and absorption improvement is necessary for vehicles, railways and generally transports, but also for computers or household appliances.

Sound energy can be dissipated thanks to porous media [1, 2] or acoustic resonators [3, 4]. Porous media are materials made of channels, cracks or cavities, which let the sound waves to travel inside the foam, thus dissipating their energy by viscous and thermal losses; these energy consumption dynamics allow sound absorption over wide frequency ranges [5, 6]. Nevertheless, they show low value of sound absorption at low-frequency applications [7].

On the contrary, acoustic resonators maximize the dissipation of the sound energy in correspondence of their resonance frequencies; thus, a source that is very localized in frequency can be easily suppressed through their introduction. Among acoustic resonators, perforated panels [8], Helmholtz resonators [9,10,11] and quarter-wavelength tubes [12] are the most used solutions. One degree-of-freedom systems like these are tunable, but they perform narrow frequency band-gaps of influence [13].

During the past decades, acoustic meta-materials and meta-surfaces [14,15,16,17] have shown several functionalities in the manipulation of sound such as negative refraction [18,19,20], sub-wavelength imaging [21,22,23], cloaking [24, 25], one-way transmittance [26], and even highly efficient sound absorption within a compact volume.

Meta-materials are made of conventional materials, such as metal and plastic, and some periodic micro-structures, that are shaped, sized and arranged in a way that affect transmission of energy and create unnatural and unconventional material properties. In this way, they can attenuate, stop or guide an elastic wave propagating in a desired path. While meta-materials are generally the combination of several media with particular shape and geometry, a meta-structure only relies on the arrangement of the local micro-structure. An acoustic meta-structure needs to be designed taking into account each acoustics phenomenon, to maximize its reliability. Furthermore, coupling a great amount of structures, like Helmholtz resonators or perforate panels, to reach high value of sound absorption in various frequency regions may result in a complex process of design and production.

In contrast, quarter-wavelength tubes are easy to tune and manufacture: indeed, they are basically cylindrical or square-section tubes with their length as main parameter for the prediction of their resonance frequencies; unfortunately, their length increases with decreasing tuning frequency, then they would be too bulk for a low-frequency industrial application. To overcome this limit, several authors have studied labyrinth resonators (LRs), where the hollow structure is made with a labyrinth shape which enables the resonance effect without increasing too much the sample thickness [27, 28]. These interesting solutions are demonstrated to be effective and smart, but the effects due to the change in shape cannot be neglected: the sound wave path is different, then the working frequency of the tubes is not the same as a classical quarter-wavelength one. On the base of this hypothesis, this work wants to demonstrate the shift in frequency of LRs respect to a single branch quarter-wavelength tube, and to formulate an improved and more reliable formula for the prediction of the resonance frequency in LRs. It is important to notice that labyrinth resonators are generally used for the absorption of a source; thus, herein, their study is limited to a single cell, made with one or more labyrinth resonators, assuming that the study of a single cell brings to the same results in the case of a more complex analysis carried out on a complete periodic structure. After all, an acoustic meta-material made with LRs with similar resonance frequencies is designed thanks to the new formulation, showing also a model with great performance in the whole audible range of frequency.

In Sect. 2, the problem is explained, discussing about the geometrical properties of the analyzed configurations; then, the Finite Elements implementation is examined. Afterwards, in Sect. 3, the results are plotted and reported.

2 Definition of the Problem

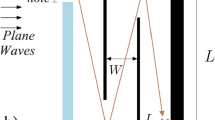
Quarter-wavelength tubes (Fig. 1) exhibit maximum absorption when the length of the tube L is equal to the quarter of the wavelength \(\lambda = c/f\), where c is the wave speed and f is the frequency.

Fig. 1.
figure 1

Example of a quarter-wavelength resonator.

Full size image

Physically explained, a hard surface can provide absorption through re-radiation of sound that is out of phase with the incident sound. When the tube length is an odd-integer multiple m of the quarter of the wavelength, the reflected wave from the bottom returns a half wavelength that is \(180^\circ \) out of phase respect to the incident wave, thus showing perfect absorption [12]. Therefore, a system like this reaches its maximum absorption when the exciting frequency is equal to one of its resonance frequencies, written as:

$$\begin{aligned} f_{res} = \frac{(2m-1)c}{4L} \end{aligned}$$
(1)

where c is the sound wave speed, almost equal to 343 \(\frac{m}{s}\) for air. This system can be very useful in order to absorb noise in low-frequency ranges, because foams are generally not so effective in such regions. The main problem is that \(\lambda \) is of the order of meters for low-frequency ranges, leading to bulky systems that are not suitable for most of acoustic applications. For instance, an exciting tone of 100 Hz can be absorbed with a tube 860 mm long; this cannot be applied in any transport configuration, but it would not be suitable for civil applications as well.

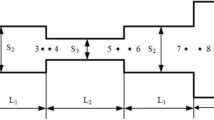
For this aim, labyrinth resonators (LRs) represent an efficient solution: a labyrinth resonator is a tube of constant width d, where the sound wave can enter, following a labyrinth path. A solution like this allows to increase the length of the tube without affecting the thickness t of the sample (Fig. 2).

Fig. 2.
figure 2

Example of a labyrinth resonator.

Full size image

A labyrinth resonator is a good compromise, and the physical phenomenon of quarter-wavelength resonance is still present; nevertheless, the wave path is changed: while the sound wave is linearly crossing the tube in the case of a single tube, the labyrinth shape forces the wave to change direction. It is reasonable to think that the resulting effective length of the wave path is not exactly equal to the whole length of the labyrinth: it may be easier to understand this concept thanks to Fig. 3, where the isobar curves of the total acoustic pressure inside a straight tube (Fig 3a)), and inside a 2D labyrinth resonator (Fig. 3b)) are represented.

Fig. 3.
figure 3

a) Isobar curves inside a quarter-wavelength tube; b) Isobar curves inside a labyrinth resonator.

Full size image

The path is clearly affected by the labyrinth; in detail, this effect mainly depends on the number of labyrinth branches n and on the dimension of the tube cross-section d. Thus, an effective length and the respective resonance frequency should be evaluated with a more accurate formula. Following the wave-path along the isobars centreline, it is possible to draw a semi-circumferential pattern in the contact zone of two adjacent branches.

Fig. 4.
figure 4

Zoom in the corner zone of a labyrinth resonator.

Full size image

This phenomenon is more clear by looking to Fig. 4: with the assumption of a 2D circular path in proximity of the connection between branches, the effective length of the labyrinth is different. Every time there is a corner, the hypothetical length was assumed as 2d; physically, it is more correct to assume wave-path length equal to \(\pi d/2\). This correction is necessary for each corner; for n labyrinth branches, there are \(n - 1\) corners. In the end, the effective length and the working frequency for \(m = 1\) have to be written respectively as:

$$\begin{aligned} L_{eff} = L - (4 - \pi ) \frac{d}{2} (n - 1) \end{aligned}$$
(2)
$$\begin{aligned} f_{res} = \frac{c}{4 \big [L - (4 - \pi )\frac{d}{2} (n-1) \big ]} \end{aligned}$$
(3)

Hereinafter, the resonance formula will be always considered for \( m = 1\). This is mainly motivated by the fact that this work is focused on low-frequency ranges, and a m-value greater than 1 leads to higher frequency values.

2.1 Geometrical Properties

The typical geometry of a labyrinth resonator is shown in Fig. 2: the plane wave radiation can easily pass through an inlet of width d, following the tube path. The passage between two branches is done with junction of height d, in order to not variate the section of the tube.

Table 1. Geometrical parameters of the analyzed configurations. The overall number of studied configurations is 97, in addition to the 12 configurations with standard tube.
Full size table

In order to prove that the new formula is more correct than the classical quarter-wave length one, four lengths (and then four resonance frequencies) are analyzed with several numbers of branches (from 2 to 10) and for three different width values d. These configurations are reported in Table 1 and compared with the 12 basic configurations with just one branch (standard quarter-wavelength tube). These 12 basic configurations are studied in order to verify if the numerical results are coherent with the analytic formula.

It is possible to notice that, from C1 to C8, the analyses are carried out for n that goes from 2 to 10, while from C9 the number of branches is limited by the length of the tube. Indeed, the height of the branches must be greater than two times the junction height 2d. Two examples of labyrinth resonators studied in this paper are reported in Fig. 5, with a nomenclature that make them easier to recognize. Indeed, CiNj stands for the \(i-\)th configuration with \(j-\)th number of labyrinth branches.

Fig. 5.
figure 5

2D configuration examples.

Full size image

2.2 Finite Element Implementation

For what concerns the FE implementation, the module “Pressure Acoustics and Frequency Domain” of COMSOL MultiPhysics is used both as modeling environment and numerical solver.

An example of a meshed LRs is represented in Fig. 6, where walls are defined as rigid (yellow colored). The 2D numerical model (xy-plane) is developed as follows: a plane wave radiation of intensity 1 Pa acts along the negative verse of y-axis in the opened branch of the labyrinth, then following the labyrinth path. Each wall has Sound Hard Boundary Wall (SHBW) as boundary condition, which means that the whole sound wave energy is reflected when it goes against the wall. The propagation of the sound wave is hence normal to the x-axis; an angle of excitation different from the one selected does not affect the labyrinthine resonance frequency; of course with a different angle, LRs harvest less energy respect to a normal excitation. Since the present study is aimed to demonstrate that the QWT resonance frequency cannot be used for LRs, a normal excitation is preferred to diffuse acoustic field or different angle excitation. A detailed description of classical FE formulation and equations can be easily found in the context of the relevant literature [29].

For all configurations reported in Table 1, the mesh consists of triangular elements generated through physics controlled algorithms that are pre-implemented in the software [30]. Nevertheless, the maximum element size of each LR meshed is always lower then 1/4 of the minimum wavelength \(\lambda \).

Fig. 6.
figure 6

Mesh example for the 2D numerical models. In detail, this is a LR with first resonance frequency at 500 Hz, with 8 branches and \(d = 5\) mm (Configuration C10N8).

Full size image
Fig. 7.
figure 7

Relative error of Eq. (1) respect to FEM results, plotted for each configuration.

Full size image
Fig. 8.
figure 8

Relative error of Eq. (3) respect to FEM results, plotted for each configuration.

Full size image

3 Discussion of Results

In this section, the results of the 12 configurations are compared respect to the analytical formulations taken by Eq. (1) and Eq. (3). Starting from the comparison between Eq. (1) and numerical results (Fig. 7), it is possible to notice that the higher the width d and the number of branches n, the bigger is its relative error respect to the Finite Element (FE) result. The numerical results are then compared with the new formula in Eq. (3), and they are reported in Fig. 8, where the maximum relative error is pair to 3.98%, much lower respect to the maximum relative error obtained with Eq. (1), which is equal to 26.26%.

Four contour plots are represented in Fig. 9; each one is a contour plot of the FE resonance frequency of Labyrinthine Resonators with the same overall length, and thus same resonance frequency according to Eq.(1), properly tuned respectively at \(f_{res} = 62.5\) in Fig. 9a, \(f_{res} = 125\) in Fig. 9b, \(f_{res} = 250\) in Fig. 9c, \(f_{res} = 500\) in Fig. 9d. It is noteworthy to highlight how each parameter markedly influence the resonance frequency of LRs, up to shift the resonance frequency of a system even above 100 Hz.

Fig. 9.
figure 9

Contour plot of resonance frequencies of LRs, varying the number of branches n ad the width of the labyrinth d.

Full size image

Furthermore, plots in Fig. 10 represent relative errors while the number of branches and the width of channels are changing. Plots on the left can be used as carpet plots; in detail, it is possible to design a labyrinth resonator making use of the subplots on the left of Fig. 10 combined with Eq. (1), instead of directly using Eq. (3). The result is the same, but contour plots may be faster to use. In contrast, plots on the right are reported in order to underline the improvement in terms of accuracy with the new formula; indeed, they are considered with the same colormap range of the respective plot on the left.

Fig. 10.
figure 10

Relative error patterns of Eq. (1) and Eq. (3) respect to FEM.

Full size image

4 Conclusions

In this work, labyrinth resonators are deeply studied because they are considered as valid replacements of quarter-wavelength tubes, the latter being very interesting objects for acoustic purposes, but limited by their inconvenient length for low-frequency applications. Going from classical quarter-wavelength tubes to LRs, it is noticed that quarter-wavelength resonance formula is not reliable for an accurate evaluation of the labyrinth resonator working frequencies. An improved formula for the prediction of their resonance frequency is proposed and demonstrated as valid, thanks to the study of 97 different cases, where the main geometrical properties of LRs are changed. The new formula is compared with the quarter-wavelength formula, proved as not acceptable for most of the LR configurations. Thus, thanks to the formula derived herein, it would be possible to properly design periodic acoustic solutions based on labyrinth resonators. A further development of the work presented herein may consist in an experimental campaign, which would constitute the final verification of the proposed formula, to make it suitable for a real application for sound absorption purposes.