Keywords

1 Introduction

The long slender structures such as risers are very important in oil and gas transportation, of which the working conditions (vortex, current, etc.) have significant risk on the lift time and safety of the structures. Vortex-induced vibrations (VIVs) and parametric resonances are two main phenomena occurred in practice, which can induce large-amplitude vibration of risers.

A number of comprehensive reviews [1,2,3] discussing VIV were focused on the single or multi-mode response, response at different Reynolds numbers, responses between multiple marine risers, impacts of the floating platforms and internal flows, etc. Previous work also highlighted that the parametric excitation of marine structures is encountered frequently, which can induce large-amplitude motions of structures as well.

With the development of technology, the impact of combined excitation from the VIV and time-varying tension has attracted significant attention in recent years. The numerical and experimental techniques are the main methods to study the response dynamics. While the semi-empirical wake oscillator models [4] are commonly used to describe the fluid-structure interactions with less cost.

In order to understand the effects of combined excitation from the vortex and varying-tension, the coupled model of the riser as well as the fluid is constructed based on the two dimensional flows in this paper. Some numerical results are given and discussion.

2 Modelling and Methodology

2.1 Model of the Structure Motion

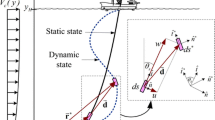
Working conditions for a TTR are complex which include excitation from currents and waves. As shown in Fig. 1, the TTR is connected to a floating platform and a wellhead, and it can move in the in-line (IL) and cross-flow (CF) directions. Herein, the TTR is modelled as a uniform Euler–Bernoulli beam simply supported at both ends as presented in Fig. 1.

Fig. 1.
figure 1

Physical model of the TTR under combined excitation

Full size image

Assuming \(\vec{r}(z,t) = X(z,t)\vec{i} + Y(z,t)\vec{j}\) denote the displacement vector of the structure, the equation of motion can be written according to the Refs. [5, 6] as

$$m_* \frac{{\partial^2 \vec{r}(z,t)}}{\partial t^2 } + \frac{\partial^2 }{{\partial z^2 }}\left( {EI\frac{{\partial^2 \vec{r}(z,t)}}{\partial z^2 }} \right) - \frac{\partial }{\partial z}\left( {T(z,t)\frac{{\partial \vec{r}(z,t)}}{\partial z}} \right) = \vec{F}_F (z,t)$$
(1)

where \(m_* = (\upmu + C_a )\uppi \uprho_f D^2 /4\) is the total mass per unit length including structural mass and added mass of fluid, \(\mu\) is the mass ratio, \(C_a\) is the coefficient of fluid added mass, \(\rho_f\) is the density of the displaced fluid, D is the outer diameter of the riser, EI is the bending stiffness. \(\vec{F}_F\) is the total fluid force acting on the structure (including the lift and drag force). \(T(z,t)\) is the varying axial tension which is calculated as \(T(z,t) = T_0 - (L - z)W_w + \Delta T\cos \upomega_p t = T_b + W_w z + \Delta T\cos \upomega_p t\), and \(T_0 ,T_b\) are the top and bottom tension of the riser.

2.2 The van der Pol Oscillator Model for the Fluid Force

In order to simulate the coupling between the structure and time-varying fluid force, the Van der Pol oscillators are introduced to represent the time-varying characteristics for the drag and lift force. The acceleration coupling is applied for the fluid oscillator.

Let \(q_x = \frac{2C_D }{{C_{D0} }},q_y = \frac{2C_L }{{C_{L0} }}\) (herein \(C_D\) and \(C_L\) denote the time-varying variables for the fluid damping and lift coefficients, \(C_{D0}\) and \(C_{L0}\) are the reference fluid damping and lift coefficients), and the wake oscillators can be written as

$$\begin{gathered} \frac{\partial^2 q_x }{{\partial t^2 }} + 2\upvarepsilon_x \Omega_f (q_x^2 - 1)\frac{\partial q_x }{{\partial t}} + 4\Omega_f^2 q_x = A_x \frac{\partial^2 X}{{\partial t^2 }} \hfill \\ \frac{\partial^2 q_y }{{\partial t^2 }} + \upvarepsilon_y \Omega_f (q_y^2 - 1)\frac{\partial q_y }{{\partial t}} + \Omega_f^2 q_y = A_y \frac{\partial^2 Y}{{\partial t^2 }} \hfill \\ \end{gathered}$$

2.3 Coupled Model of the TTR

According to Refs. [5, 6], the total fluid force \(\vec{F}_F\) induced by the lift force and fluid damping force projects on the axes x and y are derived as

$$\begin{array}{*{20}c} {(\vec{F}_F )_X = \frac{\uprho_f D}{4}\sqrt {\left( {U - \frac{\partial X}{{\partial t}}} \right)^2 + \left( {\frac{\partial Y}{{\partial t}}} \right)^2 } \left( {2C_{D0} U - 2C_{D0} \frac{\partial X}{{\partial t}} + q_x C_{D0}^{fl} U - q_x C_{D0}^{fl} \frac{\partial X}{{\partial t}} + q_y C_{L0} \frac{\partial Y}{{\partial t}}} \right)} \\ {(\vec{F}_F )_Y = \frac{\uprho_f D}{4}\sqrt {\left( {U - \frac{\partial X}{{\partial t}}} \right)^2 + \left( {\frac{\partial Y}{{\partial t}}} \right)^2 } \left( { - 2C_{D0} \frac{\partial Y}{{\partial t}} - q_x C_{D0}^{fl} \frac{\partial Y}{{\partial t}} + q_y C_{L0} U - q_y C_{L0} \frac{\partial X}{{\partial t}}} \right)} \\ \end{array}$$

Introducing the expressions of the fluid forces into Eq. (1), the coupled equations of motion the TTR can be rewritten as

$$\begin{array}{*{20}l} {m_* \frac{\partial^2 X}{{\partial t^2 }} + EI\frac{\partial^2 X}{{\partial z^4 }} - W_w \frac{\partial X}{{\partial z}} - \left( {T_b + W_w z + \Delta T\cos (\upomega_p t)} \right)\frac{\partial^2 X}{{\partial z^2 }} = } \hfill \\ {\frac{\uprho_f D}{4}\left( \begin{gathered} 2C_{D0} U^2 - 4C_{D0} U\frac{\partial X}{{\partial t}} + C_{D0}^{fl} U^2 q_x - 2C_{D0}^{fl} Uq_x \frac{\partial X}{{\partial t}} + C_{L0} Uq_y \frac{\partial Y}{{\partial t}} + 2C_{D0} (\frac{\partial X}{{\partial t}})^2 \hfill \\ + C_{D0}^{fl} q_x (\frac{\partial X}{{\partial t}})^2 - C_{L0} q_y \left( {\frac{\partial X}{{\partial t}}} \right)\left( {\frac{\partial Y}{{\partial t}}} \right) + C_{D0} \left( {\frac{\partial Y}{{\partial t}}} \right)^2 \hfill \\ \end{gathered} \right)} \hfill \\ \end{array}$$
(2)
$$\begin{array}{*{20}l} {m_* \frac{\partial^2 Y}{{\partial t^2 }} + EI\frac{\partial^2 Y}{{\partial z^4 }} - W_w \frac{\partial Y}{{\partial z}} - \left( {T_b + W_w z + \Delta T\cos (\upomega_p t)} \right)\frac{\partial^2 Y}{{\partial z^2 }} = } \hfill \\ {\frac{\uprho_f D}{4}\left( { - 2C_{D0} U\frac{\partial Y}{{\partial t}} - C_{D0}^{fl} Uq_x \frac{\partial Y}{{\partial t}} + C_{L0} U^2 q_y - 2C_{L0} Uq_y \left( {\frac{\partial X}{{\partial t}}} \right) + 2C_{D0} \left( {\frac{\partial X}{{\partial t}}} \right)\left( {\frac{\partial Y}{{\partial t}}} \right)} \right)} \hfill \\ \end{array}$$
(3)
$$\frac{\partial^2 q_x }{{\partial t^2 }} + 2\upvarepsilon_x \Omega_f (q_x^2 - 1)\frac{\partial q_x }{{\partial t}} + 4\Omega_f^2 q_x = A_x \frac{\partial^2 X}{{\partial t^2 }}$$
(4)
$$\frac{\partial^2 q_y }{{\partial t^2 }} + \upvarepsilon_y \Omega_f (q_y^2 - 1)\frac{\partial q_y }{{\partial t}} + \Omega_f^2 q_y = A_y \frac{\partial^2 Y}{{\partial t^2 }}$$
(5)

The nondimensional system can be obtained after introducing the nondimensional variables and parameters as

$$\begin{array}{*{20}l} {\frac{{\partial^2 \overline{x}}}{\partial \uptau^2 } + \frac{EI}{{m_* \upomega_0^2 L^4 }}\frac{{\partial^4 \overline{x}}}{\partial \zeta^4 } - \frac{{T_b (1 + \upbeta \cos \overline{\upomega }\uptau )}}{m_* \upomega_0^2 L^2 }\frac{{\partial^2 \overline{x}}}{\partial \zeta^2 } - \overline{r}\frac{{\partial \overline{x}}}{\partial \uptau } - \overline{r}\zeta \frac{{\partial^2 \overline{x}}}{\partial \zeta^2 } = } \hfill \\ {\frac{a\Omega_R^2 }{{2\uppi St}} - 2a\Omega_R \frac{{\partial \overline{x}}}{\partial \uptau } + \frac{b\Omega_R^2 }{{4\uppi St}}q_x - b\Omega_R q_x \frac{{\partial \overline{x}}}{\partial \uptau } + \frac{c\Omega_R }{2}q_y \frac{{\partial \overline{y}}}{\partial \uptau } + 2\uppi aSt\left( {\frac{{\partial \overline{x}}}{\partial \uptau }} \right)^2 + \uppi aSt\left( {\frac{{\partial \overline{y}}}{\partial \uptau }} \right)^2 } \hfill \\ \end{array}$$
(6)
$$\begin{array}{*{20}l} {\frac{{\partial^2 \overline{y}}}{\partial \uptau^2 } + \frac{EI}{{m_* \upomega_0^2 L^4 }}\frac{{\partial^4 \overline{y}}}{\partial \zeta^4 } - \frac{{T_b (1 + \upbeta \cos \overline{\upomega }\uptau )}}{m_* \upomega_0^2 L^2 }\frac{{\partial^2 \overline{y}}}{\partial \zeta^2 } - \overline{r}\frac{{\partial \overline{y}}}{\partial \uptau } - \overline{r}\zeta \frac{{\partial^2 \overline{y}}}{\partial \zeta^2 } = } \hfill \\ { - a\Omega_R \frac{{\partial \overline{y}}}{\partial \uptau } - \frac{b\Omega_R }{2}q_x \frac{{\partial \overline{y}}}{\partial \uptau } + \frac{c\Omega_R^2 }{{4\uppi St}}q_y - c\Omega_R q_y \frac{{\partial \overline{x}}}{\partial \uptau } + 2\uppi aSt\left( {\frac{{\partial \overline{x}}}{\partial \uptau }} \right)\left( {\frac{{\partial \overline{y}}}{\partial \uptau }} \right)} \hfill \\ \end{array}$$
(7)
$$\frac{\partial^2 q_x }{{\partial \uptau^2 }} + 2\upvarepsilon_x \Omega_R q_x^2 \frac{\partial q_x }{{\partial \uptau }} - 2\upvarepsilon_x \Omega_R \frac{\partial q_x }{{\partial \uptau }} + 4\Omega_R^2 q_x = A_x \frac{{\partial^2 \overline{x}}}{\partial \uptau^2 }$$
(8)
$$\frac{\partial^2 q_y }{{\partial \uptau^2 }} + \upvarepsilon_y \Omega_R q_y^2 \frac{\partial q_y }{{\partial \uptau }} - \upvarepsilon_y \Omega_R \frac{\partial q_y }{{\partial \uptau }} + \Omega_R^2 q_y = A_y \frac{{\partial^2 \overline{y}}}{\partial \uptau^2 }$$
(9)

where

$$\begin{gathered} \bar{x} = X/D,\bar{y} = Y/D,\uptau = \upomega _{0} t,\upzeta = z/L,\Omega _{f} = 2\uppi StU/D,\Omega _{R} = \Omega _{f} /\upomega _{0} , \hfill \\ \quad \bar{\upomega } = \upomega _{p} /\upomega _{0} ,\upbeta = \Delta T/T_{b} , \hfill \\ {\omega_1} = \sqrt { { \frac{EI{\uppi^4}}{{m_*}{L^4}}} + \frac{{T_b}{\uppi^2}}{{m_*}{L^2}}} , \omega _{R} =\omega _{1} / \omega _{0} \hfill \\\end{gathered}$$
$$\begin{gathered} \bar{r} = W_{w} /(m_{*} L\omega _{0}^{2} ),a = C_{{D0}} \rho _{f} D^{2} /(4\pi m_{*} St),b = (C_{{D0}}^{{fl}} \rho _{f} D^{2} )/(4\pi m_{*} St), \hfill \\ \quad c = (C_{{L0}} \rho _{f} D^{2} )/(4\pi m_{*} St). \hfill \\ \end{gathered}$$

\(\overline{x},\ \ \overline{y}\) are the dimensionless displacements of in-line and cross-flow motion, \(\uptau\) is the dimensionless time, \(\Omega_R\) is the dimensionless shedding frequency of vortices, \(\upomega_0\) is the reference frequency, \(\overline{\upomega }\) is the dimensionless frequency of the parametric excitation, \(\upbeta\) is the amplitude ratio of the time varying tension, \(\overline{r}\), a, b, c are the dimensionless parameters. \(\omega_{1}, \omega_{R}\) denote the dimensional and nondimensional frequency of the first-order mode.

2.4 The Galerkin Approximation

Following earlier studies [5,6,7], the approximate solutions of Eqs. (6)–(9) are obtained by employing the Galerkin approach. Here, the displacements \(\overline{x},\overline{y}\) and drag and lift coefficients \(q_x ,q_y\) are assumed as

$$\overline{x} = \sum_{n = 1}^\infty {\overline{x}_n (\tau )\overline{x}_n (\zeta ),\ \ \ \ \ \ \ \ \ \ \ \overline{y} = \sum_{n = 1}^\infty {\overline{y}_n (\tau )\overline{y}_n (\zeta )} }$$
(10)
$$q_x = \sum_{n = 1}^\infty {q_{xn} (\tau )\overline{q}_{xn} (\zeta )} ,\ \ \ \ \ \ \ \ q_y = \sum_{n = 1}^\infty {q_{yn} (\tau )\overline{q}_{yn} (\zeta )}$$
(11)

And the mode functions are assumed as

$$\overline{x}_n (\zeta ) = \overline{y}_n (\zeta ) = \overline{q}_{xn} (\zeta ) = \overline{q}_{yn} (\zeta ) = \sin (n\pi \zeta )$$

By substituting Eqs. (10)–(11) into Eqs. (6)–(9), multiplying the equations by \(\sin (n\pi \zeta )\), integrating it along the length of the riser, and applying the orthogonality of the mode functions, we can obtain the first-order approximation of the coupled system as

$$\begin{array}{*{20}l} {\ddot{\overline{x}} + 2a\Omega_R \dot{\overline{x}} + \omega_R^2 \overline{x} + \eta \beta \cos (\overline{\omega }\tau )\overline{x} = - \frac{{\overline{r}\pi^2 }}{2}\overline{x} + \frac{2a\Omega_R^2 }{{\pi^2 St}} + \frac{b\Omega_R^2 }{{4\pi St}}q_x } \hfill \\ { - \frac{8b\Omega_R }{{3\pi }}\dot{\overline{x}}q_x + \frac{4c\Omega_R }{{3\pi }}\dot{\overline{y}}q_y + \frac{16aSt}{3}\left( {\dot{\overline{x}}} \right)^2 + \frac{8aSt}{3}\left( {\dot{\overline{y}}} \right)^2 ,} \hfill \\ \end{array}$$
(12)
$$\begin{array}{*{20}l} {\ddot{\overline{y}} + a\Omega_R \dot{\overline{y}} + \omega_R^2 \overline{y} + \eta \beta \cos (\overline{\omega }\tau )\overline{y} = - \frac{{\overline{r}\pi^2 }}{2}\overline{y}} \hfill \\ { - \frac{4b\Omega_R }{{3\pi }}\dot{\overline{y}}q_x + \frac{c\Omega_R^2 }{{4\pi St}}q_y - \frac{8c\Omega_R }{{3\pi }}\dot{\overline{x}}q_y + \frac{16aSt}{3}\dot{\overline{x}}\dot{\overline{y}}} \hfill \\ \end{array}$$
(13)
$$\ddot{q}_x + 2\upvarepsilon_x \Omega_R (\frac{3q_x^2 }{4} - 1)\dot{q}_x + 4\Omega_R^2 q_x = A_x \ddot{\overline{x}}$$
(14)
$$\ddot{q}_y + \varepsilon_y \Omega_R (\frac{3q_y^2 }{4} - 1)\dot{q}_y + \Omega_R^2 q_y = A_y \ddot{\overline{y}}$$
(15)

Herein the subscript of 1 which denotes the first-order approximation is omitted in Eqs. (12)–(15) for the simplification and \(\eta = T_b \pi^2 /(m_* L^2 \omega_0^2 )\).

3 Numerical Analysis

In this part, four sets of the dynamic responses of the first-order approximation (12)–(15) are calculated under the combined resonance condition for different amplitude ratio \(\beta\). Moreover, due to excitation of the constant force, the response for the motion of in-line direction is asymmetrical. Nondimensional frequencies of Figs. 2, 3 and 4 are set as \(\overline{\omega } = 2,\omega_R = 1,\) which indicated the 1:2 parametric resonance. The other parameters are set as \(St = 0.2,\) \(\overline{r} = 0.2,\) \(A_1 = A_2 = 12,\) \(\lambda_1 = 0.3,\) \(\lambda_2 = 0.2,\eta = 0.3,\) \(a = 0.4,\) \(b = 0.04,\) \(c = 0.04\), respectively. One set of initial values are selected as [0.1, 0, 3.8, 0, 1, 0, 5, 0]. The variables for the x-axis and y-axis are the in-line and cross-flow displacements respectively.

Figure 2 shows the varying trends of the displacements of the first-order approximation of the in-line and cross-flow vibration with respective different shedding frequency \(\varOmega_R\) for the amplitude ratio \(\beta = 0\). As can be seen from Fig. 2 that the topological types of the responses exhibit different characteristics as the shedding frequency \(\varOmega_R\) increasing from 0.1 to 2.0. Specifically, for \(\varOmega_R = 0.1\) (which indicates the oncoming uniform flow is small), the displacements of the vibrations in the two directions are very small. While when \(\varOmega_R\) increases to 0.4, the values of amplitudes of the responses are increased by an order of magnitude. The similar characteristic occur for \(\varOmega_R = 0.4\) and 0.6. The more complicated responses for the motions in the two directions occur during the ‘lock-in’ frequency range, e.g. \(\varOmega_R = 0.9\) and 1.4. Continuing to increase \(\varOmega_R\) to 2.0, motions of the two directions also display the large-amplitude vibration, especially for the in-line vibration.

Fig. 2.
figure 2

The displacement orbits for the first-order approximation for \(\beta = 0\): (a) \(\varOmega_R = 0.1\); (b) \(\varOmega_R = 0.4\); (c) \(\varOmega_R = 0.6\); (d) \(\varOmega_R = 0.9\); (e) \(\varOmega_R = 1.4\); (f) \(\varOmega_R = 2.0\)

Full size image

In contrast, the dynamic responses show different characteristics when considering the impact of the time-varying tension. As shown in Figs. 3 and 4. Two sets of displacements of the motions for the structure are calculated for \(\beta = 0.2\) and 0.6, respectively as shown in Figs. 3 and 4. As shown in Fig. 3 that though the amplitude range for the two responses are similar to the case of \(\beta = 0\), the responses exhibit more complicated features as the nondimensional shedding frequency increases for \(\beta = 0.2.\) Especially for \(\varOmega_R = 0.9\) and 1.4 that during the ‘lock-in’ frequency, the relations between the displacements of motions for the in-line and cross-flow directions show more complicated state.

Fig. 3.
figure 3

The displacement orbits for the first-order approximation for \(\beta = 0.2\): (a) \(\varOmega_R = 0.1\); (b) \(\varOmega_R = 0.4\); (c) \(\varOmega_R = 0.6\); (d) \(\varOmega_R = 0.9\); (e) \(\varOmega_R = 1.4\); (f) \(\varOmega_R = 2.0\)

Full size image

Figure 4 indicates the responses are more complicated for \(\beta = 0.6\) and the coupling between the in-line and cross-flow vibration is more complicated. Moreover, the results also show that the varying tension has effect on the in-line and cross-flow vibrations. Comparing to the case for \(\beta = 0.2\), the amplitude range for the responses of the in-line and cross-flow vibration are enlarged for \(\beta = 0.6\). The combined excitation from the vortex and varying tension can induced large-amplitude vibrations of structure.

Fig. 4.
figure 4

The displacement orbits for the first-order approximation for \(\beta = 0.6\): (a) \(\varOmega_R = 0.1\); (b) \(\varOmega_R = 0.4\); (c) \(\varOmega_R = 0.6\); (d) \(\varOmega_R = 0.9\); (e) \(\varOmega_R = 1.4\); (f) \(\varOmega_R = 2.0\)

Full size image

4 Conclusions

A coupled model of a TTR excited by the vortex and varying tension is constructed, where fluid forces are modelled using two Van der Pol oscillators. The first-order approximation motion equations are derived with the Galerkin projection method. Dynamic responses of motions for the in-line and cross-flow directions are studied by the numerical method. Three sets of parameters for the amplitude ratio \(\beta\) are chosen to investigated the varying trends of the displacements in two flow directions with respect to the shedding frequency. As a comparison, \(\beta = 0\) which indicates only the effect of vortex is studied. Results showed that for \(\beta \ne 0\) (which indicates the combined excitation of the vortex and time-varying tension), the combined resonance can induced large-amplitude vibrations of the structure and the responses are more complicated. Further study about bifurcation and chaos of the system the will be followed.