Image Super-Resolution Reconstruction Based on MCA and ICA Denoising

Abstract

Image super-resolution reconstruction is a high-resolution image that is reconstructed from a low-resolution image. The learning-based algorithm is one of the more effective algorithms for image super-resolution reconstruction, and the core idea of the algorithm is to use the sample library to train the information of the image in order to increase the high-frequency information of the test image and achieve the purpose of image super-resolution reconstruction. In this paper, we propose a new image super-resolution algorithm based on morphological component analysis and dictionary learning. Firstly we make independent component analysis for image denoising processing by the K-SVD method. And then, MCA algorithm is utilized to efficiently decompose low-resolution images into texture part and structure part. And the K-SVD method is used to make dictionary training of low-resolution images. The method not only improves the robustness of the images, but also adopts different reconstruction algorithms for the different characteristics of the texture and structure parts, which better retains the details of the images and improves the quality of the reconstructed images.

1 Introduction

With the improvement of living standards, the demand for high-resolution images is increasingly urgent. In real life, limited by imaging equipment (such as cameras, camcorder), only blurry images can be obtained with very low resolution. However, clear high-resolution images are widely used in computer vision, medical images, video surveillance, and satellite imaging [1].

Since Tsai and Huang [2] first raised the issue of super-resolution reconstruction [3] in 1984, many methods of super-resolution reconstruction have emerged. It can be divided into three main categories: interpolation-based methods, reconstruction-based methods, and learning-based methods [4].

Learning-based algorithms focus more on the understanding of image content and structure than interpolation-based and reconstruction-based algorithms, utilizing more priori knowledge on images. It is through the learning of high- and low-resolution images, establishing the relationship between them, and using this relationship as a priori information to provide stronger constraints, so that better results are often obtained.

Yang et al. [5] proposed a learning algorithm based on compressed sensing [6] to obtain high and low resolution dictionary pairs D_h and D_l by directly learning image libraries; obtain the relationship between high and low resolution images by learning high and low resolution dictionary pairs. The image quality of this algorithm reconstruction is better, but the influence of the trained sample is relatively large, the training speed is slow. The effect of the reconstruction depends more on the selection of the training sample, and does not consider the characteristics of the input image itself.

Jing et al. [7] proposed a modified algorithm based on Yang et al. [5], which first decomposes the low-rate image into two parts: texture and image, using the low-resolution texture method to get the high-resolution structural picture, and the structure and texture parts are added to get the final reconstructed picture. On the basis of Jing, MCA [8] is used to decompose low-resolution pictures. MCA decomposes texture and structure more thoroughly and can obtain the image features; and bicubic interpolation as an interpolation scheme can better recover high-resolution edge information.

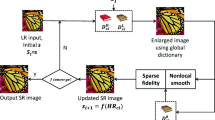
In this paper, we propose a new super-resolution reconstruction algorithm based on MCA and dictionary learning. We first use ICA [9,10,11,12] for image denoising processing. Then, decompose low-resolution images into low-resolution texture images and structure images by MCA method. Finally, train low-resolution texture images to form an over-complete dictionary. The texture image contains complex information, super resolution reconstruction method based on sparse representation.

In the feature extraction process of the dictionary training stage, the second derivative is combined with the gradient direction, and in the process of dimensionality reduction, using the 2-Dimensional principal component analysis to reduce the dimensionality, and the dictionary trained by the K-SVD algorithm is used to reconstruct the texture image [13,14,15]. The structure image is relatively flat and can be obtained using the bicubic interpolation algorithm.

Finally, overlay the reconstructed texture image and the structural image to get the final high-resolution image. Experimental results show that compared with the traditional method and Jing’s method, the proposed algorithm not only improves the convergence speed of the algorithm and the robustness of the image, but also improves the quality of the reconstructed image.

2 Methods

2.1 The ICA Basic Model

The problem of ICA $s(t) = [s_1 (t),s_2 (t), \ldots ,s_n (t)]^T$ can be described as follows. Suppose $x(t) = [x_1 (t),x_2 (t), \ldots ,x_m (t)]^T$ as the m-dimension observation signal vector, which is composed of a linear mixing of n unknown and independent source signals, where t is the discrete time and the value is as follows.

$$ X(t) = AS(t) $$

(1)

where A is a $m \times n$ dimension matrix, called a hybrid matrix switcher.

The purpose of ICA is that in the case where the mixing matrix A and the source signal $s(t)$ are unknown, the separation matrix W is determined only according to the observation data vector $x(t)$, so that each output signal $y(t) = [y_1 (t),y_2 (t), \ldots ,y_n (t)]^T$ is defined as follows, which is an estimate of the source signal vector $s(t)$. And W is a $n \times m$ dimension matrix.

$$ y(t) = Wx(t) = WAs(t) $$

(2)

2.2 Pre-processing of the Data

In general, the obtained data have correlations, so it is usually required to perform preliminary whitening or spherical processing of the data. Because the whitening process can remove the correlation between the observational signals, thereby the extraction process of subsequent independent components need to be simplified. In general, the algorithm with the data whitened converges better compared the one with the data whitening.

The random vector of a zero mean $z = (z_1 ,z_2 , \ldots ,z_M )^T$ satisfies $E\left\{ {zz^T } \right\} = I$, where I is the unit matrix. We call this vector the whitening vector. The essence of whitening is to remove correlations, which is the same as the goal of principal component analysis.

In the ICA, the independent source signals with zero mean $s(t) = [s_1 (t), \ldots ,s_N (t)]^T$ have $E\{ s_i s_j \} = E\{ s_i \} E\{ s_j \} = 0$, when $i \ne j$. And the covariance matrix is a unit matrix ${\text{cov}} \left( S \right) = I$ and the source signal $S\left( t \right)$ is white. For the observed signal, we should look for a linear transformation that is projected into a new subspace. For the observed signal $X\left( t \right)$, we should look for a linear transformation that makes $X\left( t \right)$ project into a new subspace and become a whitening vector, that is

$$ Z\left( t \right) = W_0 X\left( t \right) $$

(3)

where, $w_{_0 }$ is the whitening matrix, and Z is the whitening vector.

Using the principal component analysis, we obtain a transformation by calculating the sample vector.

$$ W_0 = \Lambda^{1/2} U^T $$

(4)

where U and $\Lambda$ represent the eigenvector matrix and the eigenvalue matrix of the covariance matrix, respectively. It can be proved that the linear transformation $W_0$ meets the requirements of the whitening transformation.

This conventional method of whitening as a pretreatment of ICA can effectively reduce the complexity of the problem, and the algorithm is simple, which can be completed with traditional PCA. Pre-processing of the whitening of the observed signals with PCA enables the original solution mixing matrix is degenerated into an orthogonal matrix, which reduces the workload of ICA. In addition, PCA itself has a dimensionality reduction function, when the number of observed signals is greater than the number of source signals, the number of observed signals can be automatically reduced to the same as the number of source signal dimensions after whitening.

2.3 The ICA Denoising Process

The ICA can decompose the received mixed signals into independent components, and the separated components are the source signals. ICA has a good processing effect in denoising [16, 17], because it basically meets the premise requirements of ICA: noise and signal are independent of each other in time, and they synthesize to observe signals together. The steps for denoising with the ICA method are as follows:

• (1) Data acquisition;

• (2) ICA decomposition: using the FastICA [18,19,20] algorithm based on negentropy, x is the original signal acquired, W is the demixing matrix, separating the independent components y one by one;

• (3) Processing results: On the basis of (2), for the decomposed independent components, according to certain signal time domain and frequency domain and other priori knowledge, useful signals and noise signals can be identified, set the component of y that belongs to the noise zero, and then the x obtained $x = W^{ - 1} y$ is the original signal that removes the noise (Fig. 1).

  Fig. 1.

  

  Independent component denoising schematic 1.

The FastICA algorithm to estimate multiple components, we can calculate in the following steps:

• 1. Centralize the observed data X, so that its mean value is O;

• 2. Whiten data X $\to$ Z;

• 3. Select the number of components to be estimated, m, and set the number of iterations p $\leftarrow$ 1;

• 4. Select an initial weight vector (random) $W_p$;

• 5. Make $W_p = E\left\{ {Zg\left( {W_p^T Z} \right)} \right\} - E\left\{ {g^{\prime}\left( {W_p^T Z} \right)} \right\}W$;

• 6. $W_p = W_p - \sum\limits_{j = 1}^{p - 1} {\left( {W_p^T W_j } \right)W_j }$;

• 7. Make $W_p = W_p /\left\| {W_p } \right\|$;

• 8. If $W_p$ does not converge, return to step 5;

• 9. Make $p = p + 1$, if $p \le m$, return to step 4.

2.4 The MCA Image Decomposition Algorithm

The main idea of MCA is to use the morphological diversity of the different features contained in the image to give an optimal sparse representation of the image morphology. MCA first extracts each morphological component of the signal separately according to the atoms in a given dictionary, and then looks for a solution to the signal decomposition inverse problem according to the sparsity constraint.

For a low-resolution image X with R pixels, MCA theory assumes that X is a linear combination of these two different parts: texture part $X_t$ and structure part $X_s$,

$$ X = X_t + X_s $$

(5)

To separate low-resolution images X containing the texture part $X_t$ and structure part $X_s$, MCA theory assumes that each part can be sparsely represented by a given dictionary, $D_t {,D}_s \in M^{R \times L}$ can be written as:

$$X_t = D_t \alpha_t,$$

(6)

$$X_s = D_s \alpha_s,$$

(7)

where $\alpha_t$ and $\alpha_s$ are the sparse representation oefficients of $X_t$ and $X_s$ in the corresponding dictionary $D_t$ and $D_s$, for the low-resolution image X containing both the texture and structure parts, we need to find an optimum sparse representation through the dictionary $D_t$ and $D_s$.

Optimum sparse representation of the low-resolution image X under the joint dictionary $\left\{ {D_t } \right.,\left. {D_s } \right\}$:

$$ \left\{ {\alpha_t^{opt} } \right.,\left. {\alpha_s^{opt} } \right\} = \arg \mathop {\min }\limits_{\left\{ {\alpha_t , \alpha_s } \right\}} {\left\| {\alpha_t } \right\|}_1 + {\left\| {\alpha_t } \right\|}_1 \;\;{\text{s}}{\rm{.t}}{.}\;\;X = D_t \alpha_t + T_s \alpha_s $$

(8)

3 Dictionary Training and Texture Image Reconstruction

Training dictionary is the most important step in image super-resolution reconstruction algorithms based on sparse representations. It will operate on the selected training library to train the dictionary corresponding to the high and low resolution. First, the second derivative is combined with the gradient direction in the feature extraction process to produce a new descent direction. An algorithm is designed with the new descending direction, which shows fast convergence speed and achieves better feature extraction results. Then dimensionality reduction in the dimension reduction process uses 2DPCA to eliminate the connection between rows and columns. Finally, complete the training with K-SVD.

3.1 2DPCA Reduces the Feature Dimension

The advantage of dimensionality reduction is energy saving in the subsequent computational training and super-resolution algorithm, before the dictionary learning reduce the dimensionality of the input low-resolution image block vectors, and the 2DPCA algorithm applied in these vectors, I expecting to retain 99% of the average information on a subspace, while retaining 99% of the patches can be projected. The algorithm is as follows:

$m \times d$ Let the size of the image matrix A be $m \times n$, $X \in R^{n \times d} \left( {n \ge d} \right)$ as a matrix, its column vector is orthogonal to each other, after the linear transformation Y = AX, the image matrix A is projected to X, will produce the projection eigenvector Y. Optimum matrix X can be found by using the total measures of dispersion sample as a criterion function $J\left( X \right)$:

$$ J\left( X \right) = tr(S_X ) $$

(9)

where $S_X$ is the covariance matrix of Y, $tr(S_X )$ for the trace of $S_X$.

$$ \begin{gathered} J(X) = tr\left\{ {E\left[ {(AX - E(AX)){(AX - E(AX))}^T } \right]} \right\} \hfill \\ = tr\left\{ {X^T E\left[ {{\left( {A - EA} \right)}^T (A - EA)} \right]X} \right\} \hfill \\ \end{gathered} $$

(10)

Then the image covariance matrix is defined as

$$ G = E\left[ {{(A - EA)}^T (A - EA)} \right] $$

(11)

Assuming that the number of training samples is M, matrix $A_i (i = 1,2,...,M)$, then the mean image is:

$$ \overline{A} = \frac{1}{M}\sum_{i = 1}^M {A_i } $$

(12)

Then the G is estimated as:

$$ G = \frac{1}{M}\sum_{i = 1}^M {{\left( {A_i - \overline{A}} \right)}^T } (A_i - \overline{A}) $$

(13)

Make $X_{opt} = \left[ {X_1 ,X_2 ,...X_d } \right]$, $X_{opt}$ is the optimum solution. After $X_{opt} = \left[ {X_1 ,X_2 ,...X_d } \right]$, feature extraction of the image, for the given A,$Y_m = AX_m$(m = 1,2,…, d).

This yields a set of later projected feature vectors, called the principal component vector of the image A.

From this, a set of projected eigenvectors $M = \left[ {Y_1 ,Y_2 ,...Y_d } \right]$ be obtained, which is called the principle component vector of image A.

3.2 K-SVD Dictionary Training

K-SVD dictionary training steps:

• 1. The high-resolution image library is under-sampling to obtain the corresponding low-resolution image library.

• 2. Extract the low-resolution image features. Images in the low-resolution image set were divided into $N\,{\times}\,N$ sized image blocks and features were extracted. The specific method is to use four one-dimensional filters:

  $$f_1 = \left[ { - 1,0,1} \right],\;\;f_2 = f_1^T$$

  (14)
  $$f_3 = \left[ { - 1,0, - 2,0,1} \right],\;\;f_4 = f_3^T$$

  (15)

  where T represents the transposition. These four 1D filters are applied to the low-resolution image, so that each image block yields 4 eigenvectors which will be concatenated as a feature representation of the image block. Through high-pass filtering preprocessing, the gradient algorithm in the optimization method was improved. When $\frac{\partial^2 f}{{\partial^2 x^2 }} \ne 0$, the second derivative and the gradient direction were combined to produce a new downward direction $d = \left[ {1 + \frac{\delta }{{\frac{\partial^2 f}{{\partial^2 x^2 }}}}} \right]\left( {\frac{\partial f}{{\partial x}}} \right)$. This method has fast convergence speed and better feature extraction effect.

• 3. Reduce the dimensionality of the resolution image with 2DPCA to train the low-resolution dictionary. Use the K-SVD algorithm train low-resolution image features into low-resolution dictionaries $D_l$.

• 4. Take the interpolated image set structure part. Interpolate the low-resolution training image to the same size as the high-resolution training image and decomposed it with MCA to obtain the structural part of the interpolated image.

• 5. Extract high-resolution image features. The remaining part of the high-resolution training image minus the low-resolution interpolated image structure part is taken as the texture part of the high-resolution image, and the texture part is divided into $\left( {RN} \right) \times \left( {RN} \right)$ sized image blocks and connected into vectors as eigenvector of the high-resolution image blocks.

• 6. Calculate a high-resolution dictionary. Assuming that high and low resolution image blocks have the same sparse representation coefficient $\alpha$ under high and low resolution dictionary pairs, the high resolution dictionary can be calculated by minimizing the lower formula approximation error:

  $$ D_h = \arg \min {\left\| {X_{_h } - D_{_h } \alpha } \right\|}_F^2 $$

  (16)

  Using Pseudo-Inverse:

  $$ D_h = X_h \alpha^+ = X_h \alpha^T {\left( {\alpha \alpha^T } \right)}^{ - 1} $$

  (17)

  where + indicates a Pseudo-Inverse.

3.3 Redeling of Texture Images

Using the obtained $D_l$ and $D_h$, low-resolution texture images can be reconstructed with high-resolution texture images. The low-resolution image is segmented according to n × n sized, and the two adjacent blocks overlap one pixel to make the corresponding adjacent high-resolution image blocks splicing smoother. The optimum sparse representation α of each block, makes $D_h \alpha$ represent the high-resolution image blocks, and this sparse representation can be solved by:

$$ \mathop {\min }\limits_\alpha \left\| {\widetilde{D}\alpha - \widetilde{y}} \right\|_2^2 + \lambda \left\| \alpha \right\|_1 $$

(18)

where $\tilde{D} = \left[ {\begin{array}{*{20}c} {D_l } \\ {PD_h } \\ \end{array} } \right]$, $\tilde{y} = \left[ {\begin{array}{*{20}c} y \\ w \\ \end{array} } \right]$, λ is the regularization coefficient, P is used to extract the overlapping area between the currently estimated high-resolution image feature block and its adjacent estimated feature block, and w represents the estimated value of the estimated high-resolution image feature block in the overlapping area. After obtaining the sparse representation $\alpha_{_i }$ of each block, $D_{_h } \alpha_{_i }$ is the corresponding high-resolution image block, and all the high-resolution image blocks are stitched together to get the final high-resolution texture image.

4 Experiment and Result Analysis

The experimental data is single, which can prove the excellent performance of the method from different aspects, and can be expressed in different forms. The effect of the denoising method on the results of the scheme should be analyzed.

In this paper, the picture Lena is utilized to compare the proposed method with the traditional linear interpolation method and Jing's algorithm respectively. In the experiment, the regularization coefficient λ was 0.15, the image block size was 5 × 5, 20000 image blocks were randomly selected for dictionary training, and the dictionary size was selected 256.

In this paper, image evaluation methods such as Peak Signal of Noise Ratio value and Structural Similarity Index Measurement value are used to evaluate the advantages and disadvantages of the reconstruction results. The results are shown in Table 1 and Table 2.

Table 1. PSNR values of different algorithms.

Table 2. SSIM values of different algorithms.

As can be seen from the table that the super-resolution reconstruction algorithm using MCA decomposition has improved PSNR and SSIM values from the traditional linear interpolation method and Jing algorithm. From Fig. 2, we can also intuitively see that the algorithm proposed in the paper has better results in details.

Fig. 2.

The performances of Bicubic interpolation (left), Algorithm of Jing (middle) and our algorithm (right).

5 Conclusions

Text first uses ICA to Image Denoising, and applies MCA decomposition method to image super-resolution reconstruction based on sparse representation, improves the feature extraction and dimensionality reduction process of dictionary training, improves the convergence rate of the algorithm.

For the texture part and the structure part, the super-resolution reconstruction based on the sparse representation learning method and the bicubic interpolation are used respectively, which not only improves the robustness of the image, but also better preserves the detail information of the image, improves the quality of the reconstructed image, and achieves a better reconstruction effect.

However, the complexity of the algorithm is higher and the speed of the puzzle is slower, which increases the time for dictionary training and image reconstruction.

In the seasonal research, we will strive to find the algorithms with low complexity but good decomposition, or improve the MCA algorithm, so that it can reduce its algorithm complexity while ensuring the decomposition.