Trajectory Tracking Control Based on RBF Neural Network Learning Control

Abstract

In this paper, a radial basis function neural network (RBFNN) learning control scheme is proposed to improve the trajectory tracking performance of a 3-DOF robot manipulator based on deterministic learning theory, which explains the parameter convergence phenomenon in the adaptive neural network control process. A new kernel function is proposed to replace the original Gaussian kernel function in the network, such that the learning speed and accuracy can be improved. In order to make more efficient use of network nodes, this paper proposes a new node distribution strategy. Based on the improved scheme, the tracking accuracy of the 3-DOF manipulator is improved, and the convergence speed of the network is improved.

1 Introduction

With the rapid development of automation, robots play an increasingly irreplaceable role in industrial manufacturing, medical and health care, daily life, military, aerospace, and other fields.

The robot manipulator is the most widely used automatic mechanical device in robot technology. Although their structures and functions are different, they are all required to track the reference signal accurately and quickly. There are strong uncertainties such as parameter perturbation, external disturbance, and unmodeled dynamics in the manipulator, which affect the trajectory tracking accuracy. Therefore, it is challenging to further improve the manipulator’s tracking accuracy.

The model-based adaptive controller can deal with the problem that the plant cannot be modeled accurately. However, it often depends on the system’s gain, the increase in gain will affect the robustness of the system and make it more sensitive to noise. Therefore, performing feedforward control of the system based on the identification model is a better choice. The neural network has a higher model approximation ability than other traditional system identification algorithms. With the rapid improvement of computing power, it is possible to use a neural network to design a feedforward controller in the trajectory tracking control process. In [1], Cong Wang proposed a deterministic learning mechanism for identifying nonlinear dynamic systems using RBF networks. When it satisfies the persistent excitation (PE) condition [2] which is proved to be satisfied when the RBFNN is persistently excited by recurrent input signals, its weights can converge to a specific range around the optimal values. The numerical control system or some manipulators in production applications repeat periodic actions. It provides an effective off-line high-precision control method for practical application scenarios.

However, deterministic learning also has some defects and deficiencies in some aspects. One of them is that its training speed is limited by the PE levels, and it often takes thousands of seconds to learn the knowledge of some complex tracking control tasks. The excessive consumption of time makes it difficult to be applied to practical production. This paper points out two standards to measure the training speed and improve the training speed of deterministic learning in two aspects: changing the structure of the RBF network and changing the distribution of nodes. By improving the kernel function in the RBF network, the training structure can meet the PE condition and reduce the amount of calculation. Furthermore, the use of nodes is improved by an optimized node distribution strategy. As a result, each node can better characterize the unknown dynamics while raising the PE levels to improve the training speed.

2 Problem Formulation and Preliminaries

This part will establish the dynamical equation of the 3-DOF manipulator and design a corresponding adaptive RBFNN controller based on the deterministic learning theory. It shows that for any periodic trajectory, the RBFNN can satisfy the PE condition with appropriate parameter selection.

2.1 3-DOF Manipulator Model

The selected three-link manipulator model is shown in Fig. 1. For the link $i\left( i=1,2,3 \right)$, ${{m}_{i}}$ represents the mass, ${{l}_{i}}$ is the length, ${{\theta }_{i}}$ represents the angle of each link joint with the vertical direction, ${{J}_{i}}$ is the moment of inertia of each link perpendicular to the XY plane, ${{l}_{ci}}$ is the distance from the head joint its center of gravity.

Fig. 1.

Structure of three-link manipulator.

Using Newton-Euler equation, the dynamic equation of three-link manipulator can be expressed as follows:

$$\begin{aligned} M\left( \theta \right) \ddot{\theta }+C\left( \theta ,\dot{\theta } \right) \dot{\theta }+G\left( \theta \right) =\tau \end{aligned}$$

(1)

where $M\left( \theta \right) \in {{\mathbb {R}}^{3\times 3}}$ is the inertia matrix, which meets the positive definiteness and symmetry, $C\left( \theta ,\dot{\theta } \right) \in {{\mathbb {R}}^{3\times 3}}$ is the combination vector of Coriolis force and centrifugal force; $G\left( \theta \right) \in {{\mathbb {R}}^{3\times 1}}$ is the gravity matrix. $\ddot{\theta }\ \text {=}\ {{\left[ {{\begin{matrix} {{{\ddot{\theta }}}_{1}} &{} {{{\ddot{\theta }}}_{2}} &{} {\ddot{\theta }} \\ \end{matrix}}_{3}} \right] }^{T}}$ is the angular acceleration vector of the system, and $\dot{\theta }\ \text {=}\ {{\left[ {{\begin{matrix} {{{\dot{\theta }}}_{1}} &{} {{{\dot{\theta }}}_{2}} &{} {\dot{\theta }} \\ \end{matrix}}_{3}} \right] }^{T}}$ is the angular velocity vector of the system, $\tau \ \text {=}\ {{\left[ {{\begin{matrix} {{\tau }_{1}} &{} {{\tau }_{2}} &{} \tau \\ \end{matrix}}_{3}} \right] }^{T}}$ is the control torque vector [3, 4].

$M\left( \theta \right)$:

$$\begin{aligned} M\left( \theta \right) =\left[ \begin{matrix} {{\alpha }_{11}} &{} {{\alpha }_{12}}{{C}_{21}} &{} {{\alpha }_{13}}{{C}_{31}} \\ {{\alpha }_{1}}_{2}{{C}_{21}} &{} {{\alpha }_{22}} &{} {{\alpha }_{23}}{{C}_{32}} \\ {{\alpha }_{13}}{{C}_{31}} &{} {{\alpha }_{23}}{{C}_{32}} &{} {{\alpha }_{33}} \\ \end{matrix} \right] \end{aligned}$$

(2)

where $\alpha ,S,C$ are fixed parameters:

$$\begin{aligned} \left\{ \begin{aligned}&{{\alpha }_{11}}={{J}_{1}}+{{m}_{1}}{{l}_{c1}}^{2}+({{m}_{2}}+{{m}_{3}}){{l}_{1}}^{2} \\&{{\alpha }_{12}}=\left( {{m}_{2}}{{l}_{c2}}+{{m}_{3}}{{l}_{2}} \right) {{l}_{1}} \\&{{\alpha }_{13}}={{m}_{3}}{{l}_{1}}{{l}_{c3}} \\&{{\alpha }_{22}}={{J}_{2}}+{{m}_{2}}{{l}_{c2}}^{2}+{{m}_{3}}{{l}_{2}}^{2} \\&{{\alpha }_{23}}={{m}_{3}}{{l}_{2}}{{l}_{c3}} \\&{{\alpha }_{33}}={{J}_{3}}+{{m}_{3}}{{l}_{c3}}^{2} \\ \end{aligned} \right. \end{aligned}$$

(3)

$$\begin{aligned} \left\{ \begin{matrix} {{S}_{i}}=\sin {{\theta }_{i}},{{S}_{ij}}=\sin \left( {{\theta }_{i}}-{{\theta }_{j}} \right) \\ {{C}_{i}}=\cos {{\theta }_{i}},{{C}_{ij}}=\cos \left( {{\theta }_{i}}-{{\theta }_{j}} \right) \\ \end{matrix} \right. \end{aligned}$$

(4)

$C\left( \theta ,\dot{\theta } \right)$:

$$\begin{aligned} C\left( \theta ,\dot{\theta } \right) =\left[ \begin{matrix} 0 &{} -{{\alpha }_{12}}{{{\dot{\theta }}}_{2}}{{S}_{21}} &{} -{{\alpha }_{13}}{{{\dot{\theta }}}_{3}}{{S}_{31}} \\ {{\alpha }_{12}}{{{\dot{\theta }}}_{1}}{{S}_{21}} &{} 0 &{} -{{\alpha }_{23}}{{{\dot{\theta }}}_{3}}{{S}_{32}} \\ {{\alpha }_{13}}{{{\dot{\theta }}}_{1}}{{S}_{31}} &{} {{\alpha }_{23}}{{{\dot{\theta }}}_{2}}{{S}_{32}} &{} 0 \\ \end{matrix} \right] \end{aligned}$$

(5)

where g is the gravitational acceleration, and the formation $G\left( \theta \right)$ are:

$$\begin{aligned} G\left( \theta \right) ={{\left[ \begin{matrix} -{{\beta }_{1}}{{S}_{1}} &{} -{{\beta }_{2}}{{S}_{2}} &{} -{{\beta }_{3}}{{S}_{3}} \\ \end{matrix} \right] }^{T}} \end{aligned}$$

(6)

where

$$\begin{aligned} \left\{ \begin{aligned}&{{\beta }_{1}}=\left( {{m}_{1}}{{l}_{c1}}+{{m}_{2}}{{l}_{1}}+{{m}_{3}}{{l}_{1}} \right) g \\&{{\beta }_{2}}=\left( {{m}_{2}}{{l}_{c2}}+{{m}_{3}}{{l}_{2}} \right) g \\&{{\beta }_{3}}={{m}_{3}}{{l}_{c3}}g \\ \end{aligned} \right. \end{aligned}$$

(7)

The three-link manipulator model can be built based on the above dynamic equations and parameters.

2.2 RBF Neural Network and Deterministic Learning

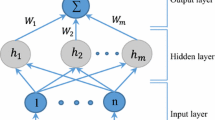
RBF neural network has a good approximation ability. Theoretically, with enough neurons it can approximate any $\Sigma$-Borel measure nonlinear function with arbitrary precision in the compact set [5]. Generally, an RBF neural network can be expressed as:

$$\begin{aligned} {{f}_{nn}}\left( Z \right) =\sum \limits _{i=1}^{N}{{{w}_{i}}{{s}_{i}}\left( Z \right) }={{W}^{T}}S\left( Z \right) \end{aligned}$$

(8)

where $Z\in {{\varOmega }_{Z}}\subset {{\mathbb {R}}^{n}}$ is the input vector of the neural network, N is the number of network nodes, $W=\left[ {{w}_{1}},{{w}_{2}},\ldots ,{{w}_{N}} \right] \in {{\mathbb {R}}^{N}}$ is the weight vector, $S\left( Z \right) ={{\left[ {{s}_{1}}\left( \left\| Z-{{\xi }_{1}} \right\| \right) ,\ldots , {{s}_{N}}\left( \left\| Z-{{\xi }_{N}} \right\| \right) \right] }^{T}}$ represents the regressor vector of the neural network, ${{s}_{i}}\left( \cdot \right) \left( i=1,\ldots ,N \right)$ describes the RBF, where ${{\xi }_{i}}\left( i=1,\ldots ,N \right)$ is the center of each neuron function. The most commonly used RBF is the Gaussian RBF [6], which is expressed as follows:

$$\begin{aligned} {{s}_{i}}\left( \left\| Z-{{\xi }_{i}} \right\| \right) =\exp \left[ \frac{-{{\left( Z-{{\xi }_{i}} \right) }^{T}}\left( Z-{{\xi }_{i}} \right) }{{{\eta }_{i}}^{2}} \right] \end{aligned}$$

(9)

where ${{\eta }_{i}}$ indicates the width of the function receptive field.

The single axis of a three-link manipulator is considered, and its order is set as 2. The nonlinear system in Brunovsky form is as follows:

$$\begin{aligned} \left\{ \begin{aligned}&{{{\dot{x}}}_{1}}={{x}_{2}} \\&{{{\dot{x}}}_{2}}=f\left( x \right) +u \\ \end{aligned} \right. \end{aligned}$$

(10)

where $x={{\left[ {{x}_{1}},{{x}_{2}} \right] }^{T}}\in {{\mathbb {R}}^{2}},u\in \mathbb {R}$ is state variable and system input respectively, $f\left( x \right)$ is an unknown smooth nonlinear function, which can be approximated by RBF network (8).

Consider the second-order reference model:

$$\begin{aligned} \left\{ \begin{aligned}&{{{\dot{x}}}_{{{d}_{1}}}}={{x}_{{{d}_{2}}}} \\&{{{\dot{x}}}_{{{d}_{2}}}}={{f}_{d}}\left( {{x}_{d}} \right) \\ \end{aligned} \right. \end{aligned}$$

(11)

where ${{x}_{d}}={{\left[ {{x}_{{{d}_{1}}}},{{x}_{{{d}_{2}}}} \right] }^{T}}\in {{\mathbb {R}}^{2}}$ is the system state, ${{f}_{d}}\left( \cdot \right)$ is a known smooth nonlinear function. The system’s trajectory starting from the initial condition ${{x}_{d}}\left( 0 \right)$ is denoted by ${{\varphi }_{a}}\left( {{x}_{d}}\left( 0 \right) \right)$ (also as ${{\varphi }_{d}}$ for brevity). Assume that the states of the reference model are uniformly bounded, i.e., ${{x}_{d}}\left( t \right) \in {{\varOmega }_{d}},\forall t\ge 0$, and the system orbit ${{\varphi }_{d}}$ is assumed to be a periodic motion [1].

The adaptive neural controller using the Gaussian RBF network is expressed as:

$$\begin{aligned} u=-{{z}_{1}}-{{c}_{2}}{{z}_{2}}-{{\hat{W}}^{T}}S\left( Z \right) +{{\dot{\alpha }}_{1}} \end{aligned}$$

(12)

where

$$\begin{aligned} \left\{ \begin{aligned}&{{z}_{1}}={{x}_{1}}-{{x}_{{{d}_{1}}}} \\&{{z}_{2}}={{x}_{2}}-{{\alpha }_{1}} \\&{{\alpha }_{1}}=-{{c}_{1}}{{z}_{1}}+{{{\dot{x}}}_{{{d}_{1}}}}=-{{c}_{1}}{{z}_{1}}+{{x}_{{{d}_{2}}}} \\&{{{\dot{\alpha }}}_{1}}=-{{c}_{1}}{{{\dot{z}}}_{1}}+{{{\dot{x}}}_{{{d}_{2}}}}=-{{c}_{1}}\left( -{{c}_{1}}{{z}_{1}}+{{z}_{2}} \right) +{{f}_{d}}\left( {{x}_{d}} \right) \\ \end{aligned} \right. \end{aligned}$$

(13)

${{c}_{1}},{{c}_{2}}>0$ is the control gain, $Z=x={{\left[ {{x}_{1}},{{x}_{2}} \right] }^{T}}$ is the network input.

${{W}^{*}}$ is ideal constant weights and $\hat{W}$ is the estimated value of weights ${{W}^{*}}$ of RBF network. Let $\tilde{W}=\hat{W}-{{W}^{*}}$, and its update rate is:

$$\begin{aligned} \dot{\hat{W}}=\dot{\tilde{W}}=\varGamma \left( S\left( Z \right) {{z}_{2}}-\sigma \hat{W} \right) \end{aligned}$$

(14)

where $\varGamma ={{\varGamma }^{T}}>0$ is a design matrix, $\sigma$ is a small positive value.

PE condition is an essential concept in adaptive control systems.In the study of adaptive control, the PE condition played an essential role in the convergence of controller parameters. It is defined as follows:

A piecewise-continuous, uniformly bounded, the vector-valued function $S:\left[ \left. 0,\infty \right) \right. \rightarrow {{\mathbb {R}}^{n}}$ is said to satisfy the PE condition if there exist positive constants ${{T}_{0}}$,${{\alpha }_{1}}$ and ${{\alpha }_{2}}$ such that:

$$\begin{aligned} {{\alpha }_{1}}I\le \int _{{{t}_{0}}}^{{{t}_{0}}+{{T}_{0}}}{S\left( \tau \right) }S{{\left( \tau \right) }^{T}}d\tau \le {{\alpha }_{2}}I \end{aligned}$$

(15)

holds for $\forall {{t}_{0}}>0$, where $I\in {{\mathbb {R}}^{n\times n}}$ is the identity matrix [2].

It has been proved that almost any periodic or quasi-periodic trajectory can satisfy the partial PE condition of the corresponding RBF regressor vector [7].

When RBF neural network is applied locally, $f\left( Z \right)$ can be approximated by a limited number of neurons involved in a particular region of trajectory Z:

$$\begin{aligned} f\left( Z \right) ={{W}_{\xi }}^{*T}{{S}_{\xi }}\left( Z \right) +{{e}_{\xi }} \end{aligned}$$

(16)

${{S}_{\xi }}\left( Z \right) ={{\left[ {{\text {s}}_{j1}}\left( Z \right) ,\ldots ,{{\text {s}}_{j\xi }}\left( Z \right) \right] }^{T}}\in {{\mathbb {R}}^{{{N}_{\xi }}}}\left( {{N}_{\xi }}<N \right)$,$\left| {{s}_{ji}} \right|>\tau \left( i=1,\ldots ,\xi \right) ,\tau >0$ is a small positive constant, ${{W}_{\xi }}^{*}={{\left[ {{w}_{j1}}^{*},\ldots ,{{w}_{j\xi }}^{*} \right] }^{T}}$, ${{e}_{\xi }}$ is the error caused by approximation. That is to say, ${{S}_{\xi }}\left( Z \right)$ is a dimension-reduced subvector of $S\left( Z \right)$.

Since the input of the manipulator follows a cyclic (or quasi-cyclic) trajectory, it can be proved in [8] that the RBF neural network satisfies the local PE condition.

In deterministic learning theory, the neural weight estimation ${{\hat{W}}_{\xi }}$ converges to its optimal value ${{W}_{\xi }}^{*}$, and the locally accurate ${{\hat{W}}^{T}}S\left( Z \right)$ approximation of the dynamic system ${{f}_{g}}\left( x \right)$ along the trajectory ${{\varphi }_{\zeta }}\left( x\left( T \right) \right)$ is obtained by reaching the error level ${{e}^{*}}$.

$$\begin{aligned} \bar{W}=mea{{n}_{t\in \left[ {{t}_{a}},{{t}_{b}} \right] }}\hat{W}\left( t \right) \end{aligned}$$

(17)

where $\left[ {{t}_{a}},{{t}_{b}} \right]$ with ${{t}_{b}}>{{t}_{a}}>T$ represents a time segment after the transient process.

3 Methods to Improve Training Speed

The low training speed is the disadvantage of deterministic learning, and it is caused by the irrational distribution of the neural network. In the process of applying deterministic learning theory, the training speed can be reflected in two aspects:

• Weights Convergence: according to the deterministic learning theory, the weights will eventually converge when the PE condition is satisfied. The earlier the weights join, the faster it can approach the inverse model of the plant, and the tracking error can be reduced to a reasonable range.

• Convergence of tracking error: after the weight has converged or is close to convergence, the tracking error of the plant will generally decrease with the training process. The shorter the tracking error can be reduced to a reasonable range, the faster the training speed will be.

To improve the training speed of deterministic learning, this paper considers two aspects: one is to change the RBF’s structure and find a scheme to replace the Gaussian kernel function, the other is to propose a method to calculate the radius of curvature from scattered data, to design the node distribution.

3.1 Change the Structure of the Network

The periodicity of the input signal $Z\left( t \right)$ makes ${{S}_{\zeta }}\left( Z \right)$ satisfy the PE condition, but this is usually not the PE condition of the entire regressor vector $S\left( Z \right)$. According to the adaptive law (14), the whole closed-loop system can be summarized as follows:

$$\begin{aligned} \left[ \begin{matrix} {\dot{z}} \\ {\dot{\tilde{W}}} \\ \end{matrix} \right] =\left[ \begin{matrix} A &{} -bS{{\left( Z \right) }^{T}} \\ \varGamma S\left( Z \right) {{b}^{T}} &{} 0 \\ \end{matrix} \right] \left[ \begin{matrix} z \\ {\tilde{W}} \\ \end{matrix} \right] +\left[ \begin{matrix} be \\ -\sigma \varGamma \hat{W} \\ \end{matrix} \right] \end{aligned}$$

(18)

where $z={{\left[ {{z}_{1}},{{z}_{2}} \right] }^{T}},\tilde{W}=\hat{W}-{{W}^{*}}$ are the states,A is an asymptotically stable matrix expressed as

$$\begin{aligned} A=\left[ \begin{matrix} -{{c}_{1}} &{} 1 \\ -1 &{} -{{c}_{2}} \\ \end{matrix} \right] \end{aligned}$$

(19)

which satisfies $A+{{A}^{T}}=-Q<0,b={{\left[ 0,1 \right] }^{T}},\left( A,b \right)$ is controllable, $\varGamma ={{\varGamma }^{T}}>0$ is a constant matrix. Then we have:

$$\begin{aligned} {{\dot{\hat{W}}}_{{\bar{\zeta }}}}={{\dot{\hat{W}}}_{{\bar{\zeta }}}}={{\varGamma }_{{\bar{\zeta }}}}\left( {{S}_{{\bar{\zeta }}}}\left( Z \right) {{z}_{2}}-\sigma {{{\hat{W}}}_{{\bar{\zeta }}}} \right) \end{aligned}$$

(20)

From [9,10,11], PE of ${{S}_{\zeta }}\left( Z \right)$ leads to the exponential stability of $\left( z,{{{\tilde{W}}}_{\zeta }} \right) =0$ for the nominal part of the system (18). $\left| \left| {{e}^{'}}_{\zeta } \right| -\left| {{e}_{\zeta }} \right| \right|$ is small, and $\sigma {{\varGamma }_{\zeta }}{{\hat{W}}_{\zeta }}$ can be made small by choosing a small $\sigma$ [12].

Selecting $\bar{W}$ according to (17), the convergence of ${{\hat{W}}_{\zeta }}$ to a small neighborhood of ${{W}_{\zeta }}^{*}$ indicates along the orbit ${{\varphi }_{\zeta }}\left( x\left( T \right) \right)$, we have:

$$\begin{aligned} \begin{aligned}&f\left( x \right) =f\left( Z \right) ={{W}_{\zeta }}{{^{*}}^{T}}{{S}_{\zeta }}\left( Z \right) +{{e}_{\zeta }}={{{\hat{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) -{{{\tilde{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) +{{e}_{\zeta }} \\&\text { }={{{\hat{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) +{{e}_{\zeta 1}}={{{\bar{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) +{{e}_{\zeta 2}} \\ \end{aligned} \end{aligned}$$

(21)

where ${{e}_{\zeta 1}}={{e}_{\zeta }}-{{\tilde{W}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right)$ is close to ${{e}_{\zeta }}$ due to the convergence of ${{\tilde{W}}_{\zeta }}$, ${{\bar{W}}_{\zeta }}={{\left[ {{{\bar{w}}}_{{{j}_{1}}}},\ldots ,{{{\bar{w}}}_{{{j}_{\zeta }}}} \right] }^{T}}$ is the subvector of $\bar{W}$, using ${{\bar{W}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right)$ to approximate the whole system, then ${{e}_{\zeta 2}}$ is the error.

After time T, $\left| \left| {{e}_{\zeta 2}} \right| -\left| {{e}_{\zeta 1}} \right| \right|$ is small. Besides, neurons whose center is far away from the track ${{\varphi }_{\zeta }}$, $\left| {{S}_{{\bar{\zeta }}}}\left( Z \right) \right|$ will become very small due to the localization property of the RBF network. From the law (20) and $\hat{W}\left( 0 \right) =0$, the small values of ${{S}_{{\bar{\zeta }}}}\left( Z \right)$ will make the neural weights ${{\hat{W}}_{{\bar{\zeta }}}}$ activated and updated only slightly. Since many data are small, there is:

$$\begin{aligned} \begin{aligned}&f\left( Z \right) ={{W}_{\zeta }}{{^{*}}^{T}}S\left( Z \right) +{{e}_{\zeta }} \\&\text { }={{{\hat{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) +{{{\hat{W}}}_{{\bar{\zeta }}}}^{T}{{S}_{{\bar{\zeta }}}}\left( Z \right) +{{e}_{1}}={{{\hat{W}}}^{T}}S\left( Z \right) +{{e}_{1}} \\&\text { }={{{\bar{W}}}_{\zeta }}^{T}{{S}_{\zeta }}\left( Z \right) +{{{\bar{W}}}_{{\bar{\zeta }}}}^{T}{{S}_{{\bar{\zeta }}}}\left( Z \right) +{{e}_{2}}={{{\bar{W}}}^{T}}S\left( Z \right) +{{e}_{2}} \\ \end{aligned} \end{aligned}$$

(22)

It is seen that both the RBF network ${{\hat{W}}^{T}}S\left( Z \right)$ and ${{\bar{W}}^{T}}S\left( Z \right)$ can approximate the unknown $f\left( x \right) =f\left( Z \right)$.

From the above process of proving the weights convergence, it can be found that the requirement for the RBF is only its localized structure, so the selection of the RBF can be more extensive. Considering that most of the radial basis functions used in the original RBF network are Gaussian kernels, the deterministic learning theory also continues to use Gaussian kernels when proposed. However, considering the computational complexity, the Gaussian kernel function is not necessarily the optimal solution in all cases.

Quadratic rational kernel is also commonly used radial basis functions:

$$\begin{aligned} {{s}_{i}}\left( \left\| Z-{{\xi }_{i}} \right\| \right) =1-\frac{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}}{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}+c} \end{aligned}$$

(23)

where $Z\in {{\varOmega }_{Z}}\subset {\mathbb {R}^{n}}$ is the input vector of the neural network, ${{\xi }_{i}}\left( i=1,\ldots ,N \right)$ is the center of each neuron function.

Since the unknown quantity c in the quadratic rational kernel function is a constant, we have:

$$\begin{aligned} {{s}_{i}}\left( \left\| Z-{{\xi }_{i}} \right\| \right) =1-\frac{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}}{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}+c}=\frac{c}{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}+c} \end{aligned}$$

(24)

Let $\left\| Z-{{\xi }_{i}} \right\| =t$, comparing the computational complexity of (9), (24), it can be found that the computational complexity of quadratic rational kernel function is $o\left( {{t}^{2}} \right)$, while the computational complexity of Gaussian kernel function is $o\left( {{e}^{t}} \right)$. With the increase of t, the computational complexity $o\left( {{e}^{t}} \right) >o\left( {{t}^{2}} \right)$. Therefore, when the number of nodes i is kept constant, the computational complexity of applying the Gaussian kernel function is more than that of the quadratic rational kernel function.

For the quadratic rational kernel function, if the constant n is introduced, there is ${{s}_{i}}\left( \left\| Z-{{\xi }_{i}} \right\| \right) =1-\frac{n*{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}}{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}+c}$. The approximation accuracy of the network is further improved by changing the value of the constant n.

3.2 Change the Distribution Strategy of Nodes

The nonlinear approximation ability of the neural network will be improved with the increase of the node density. On the other hand, an excessive number of nodes will affect the training speed. Therefore, under the same approximation accuracy, reducing the number of nodes can effectively improve the training speed of the RBF network.

In the deterministic learning theory, the reference input of RBF model training is generally selected as the required position information and its first and second derivative information (velocity and acceleration information). A certain point in the three-dimensional space thus constructed can represent their position, velocity, and acceleration information at the current time. The selection of network nodes is based on this three-dimensional space. There are two modes for the distribution of RBF network nodes:

• Distributed by regular lattice: Only the area occupied by the input information of the RBF network in the three-dimensional space needs to be considered, as shown in Fig. 2.

• Distributed along the input signal: This distribution model is evenly distributed along the input track, as shown in Fig. 3, which can better use each nodes.

Fig. 2.

Nodes are distributed by lattice.

Fig. 3.

Nodes are evenly distributed by input.

The curvature information can be used to represent the complexity of input signal. In the space composed of three-dimensional input information, the part where the curve changes sharply is usually the position where the radius of curvature is small. Therefore, more nodes should be distributed around the parts with larger curvature (smaller curvature radius) to improve the approximation accuracy, and the node width can be reduced accordingly.

For curve $y=f\left( x \right)$, the commonly used curvature calculation formula is $K=\frac{\left| {\ddot{y}} \right| }{{{\left( 1+{{{\dot{y}}}^{2}} \right) }^{\frac{3}{2}}}}$, where $\dot{y},\ddot{y}$ are the first and second derivatives of y to x. However, the limitation of this method is that it is only applicable to continuous functions. The problem with this method is that the curve fitting will lose part of the input signal information, resulting in the decline of approximation accuracy. When calculating the curvature of the local position, it is also easy to receive the interference of noise and other information to produce peaks, which is not conducive to the approximation of the network.

Therefore, consider a new way to define the curvature for the scattered points in space. For three points A, B, C in state space, their time sequence is A passes through B to C. When the angle formed by $\angle ABC$ is an acute angle or right angle, the schematic diagram is as follows:

Since the coordinates of points A, B, C in the input data are known, the size of $\left| AB \right| ,\left| BC \right| ,\left| AC \right|$ in space can be obtained. Let $\left| AC \right| ={{l}_{b}}$, $\angle ABC=\angle \theta$. Let the center of the circumscribed circle passing through the three points be O and the radius be R, thus the radius of curvature obtained from the three points A, B, C in the definition space be the circumscribed circle radius R.

To obtain the size of radius R, connect segment OA, OB, OC, and OH is the vertical line of AC. Then at $\angle \theta \le 90{}^\circ$, it can be known from the geometric relationship:

$$\begin{aligned} \angle ABO+\angle CBO+\angle OAC=90{}^\circ \end{aligned}$$

(25)

where $\angle ABO+\angle CBO=\angle \theta$, can get $\angle AOH=\angle COH=\angle \theta$. In $\Delta AOH$, we can calculate the newly defined radius of curvature of the scatter:

$$\begin{aligned} R=\frac{{{l}_{b}}}{2\sin \left( \theta \right) } \end{aligned}$$

(26)

When $\angle \theta >90{}^\circ$, the transition from $\overrightarrow{AB}$ to $\overrightarrow{BC}$ is smooth and the corresponding radius of curvature is large, the calculation results of the above formula conform to this feature.

When the variation trend of scattered points with time is more intense, the result obtained from (26) is smaller. When the variation trend of spray with time is flat, the result is larger. Define a threshold T, when the radius of curvature $R<T$, the nodes distribution spacing and the scope of action are reduced, and the nodes distribution spacing is increased at other positions to reduce the number of nodes. In this way, the complex signal can be approximated more accurately while maintaining a certain number of nodes, which saves computing power and improves the approximation accuracy (Fig. 4).

Fig. 4.

Calculation of radius of curvature of scattered points.

Fig. 5.

Tracking error of three-axis manipulator.

4 Experiment and Analysis

4.1 Experimental Result

1) Experiment preparation: Input $x=\sin \left( t \right) ; y=\cos \left( t \right) ; z=\sin \left( t \right)$ to the three axes of the three-link manipulator model for training. Figure 5 shows the system’s three-axis tracking error comparison data using only PID control and in addition with the original deterministic learning control.

2) Change the RBF network structure: The Gaussian kernel function in the RBF network is replaced by the modified quadratic rational kernel function ${{s}_{i}}\left( \left\| Z-{{\xi }_{i}} \right\| \right) =1-\frac{n*{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}}{{{\left\| Z-{{\xi }_{i}} \right\| }^{2}}+c}$, and $n=2.5; c=1.5$ is selected through experimental comparison.

The three-axis input signals are $x=\sin \left( t \right) ; y=\cos \left( t \right) ; z=\sin \left( t \right)$ respectively. For axis 3 of the three-link manipulator, Fig. 6 and Fig. 7 show the weights convergence of the Gaussian kernel and the modified quadratic rational kernel. Figure 8 is a comparison diagram of the tracking error between the Gaussian kernel function and the modified quadratic rational kernel function.

Fig. 6.

Axis 3’s weights of manipulator using Gaussian kernel.

Fig. 7.

Axis 3’s weights of manipulator using the modified quadratic rational kernel.

Fig. 8.

Axis 3’s tracking error comparison.

Fig. 9.

3-DOF manipulator input track.

3) Change the distribution strategy of nodes: The crown trajectory is selected as the input of the 3-DOF manipulator, as shown in Fig. 9, where X, Y, Z are the position information of each axis.

In one trajectory period of axis 3, the value of the radius of curvature of the scatter can be obtained, as shown in Fig. 10.

Set the threshold T to 20, and increase the node distribution density when the threshold is less than 20.

Figure 11 shows the error comparison of axis 3 according to two distribution modes when the number of nodes is 41.

Fig. 10.

Curve of curvature radius (axis 3).

Fig. 11.

Comparison of tracking errors between two node distribution methods.

4.2 Experimental Analysis

From the above experimental results, it can be seen that in the simulation with the three-link manipulator model as the plant, compared with the original RBF network, the method of changing the RBF network’s kernel function has the following advantages:

• The weight convergence speed of the improved RBF network is faster than that of the original one. The weight convergence speed will significantly affect the network’s speed approaching the inverse model of the plant. Therefore, its error reduction rate is higher than the original network, effectively improving the training speed, reducing computing power and saving time.

• Compared with the original RBF network, the approximation accuracy of the improved RBF network is also enhanced. In the simulation experiment, the tracking error can be reduced to ${{10}^{-6}}$ in a short time.

Changing the node distribution strategy also has the following advantages: It is often necessary to distribute a larger number of nodes for those complex input trajectories. This method can optimize the distribution of nodes by applying the same number of nodes, thereby improving the tracking accuracy, on the premise of the same tracking accuracy, it can reduce the number of nodes, speeding up the training.

5 Conclusion

Under the framework of deterministic learning theory, this paper modifies the RBF network structure of the feedforward-feedback control loop part, proposes a modified quadratic rational kernel function to replace the Gaussian kernel function in the RBF network which is suitable for the 3-DOF manipulator. By optimizing the network structure, periodic signals’ training speed and tracking accuracy are improved. A new definition of the curvature radius is presented, and the node distribution strategy is optimized on this basis, which can make better use of nodes and save computing power. Experiments verify the effectiveness of the improved strategy.