Keywords

1 Introduction

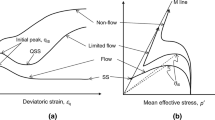
Investigation of soil behaviour is broadly carried out at two different levels, which are macro and micro. Macro level is the level at which most of the constitutive models available in literature are defined/formulated using stress-strain invariants in a phenomenological way. However, even though the quantitative observation of the macro level soil response is relatively easy and enables the development of constitutive formulations which create an interface between theory and experiments in a straightforward way, they can only provide limited physical information serving as an expression of the possibilities emerging from granular (micro) level behaviour. On the other hand, recent micro level numerical (e.g., discrete element method, DEM) and experimental (e.g., X-ray computed tomography) studies provide promising results/findings for further developments in the field of soil mechanics. However, for the time being, these advanced experimental test setups only account for the kinematics of particles (i.e., only particle motion without contact forces between them). Advanced physics based discrete element simulations can render all types of granular information (i.e., kinematics and forces), but due to their computational efficiency, they are far from being an alternative for finite element simulations, especially for the investigation of field scale boundary value problems (BVPs). This work aims to provide a “physical” link between micro and macro level behaviours to provide robust and realistic predictions for anisotropic soil behaviour within the boundaries of continuum mechanics. Beyond the classical constitutive modelling approach in continuum mechanics where the stress and strain tensors are defined on a unit cube, a so-called multilaminate approach approximating a unit sphere has been used, Fig. 1. As a result, a direction dependent nonlinear behaviour of soil is formulated, not by using 3 surfaces, but many surfaces which will be referred to as sampling planes hereafter. These surfaces can be considered as selected planes where the micromechanical observations are approximated.

In this work, the proposed model does not claim to reproduce meso or micro level behaviour of soil, but instead provides an interface between continuum (macro) and micro scales through the use of sampling planes.

2 Multilaminate Framework

In this paper, the direction dependent behaviour of soil is formulated using the slip theory based multilaminate framework, which was originally developed by Pande and Sharma (1983) for the investigation of cohesive soils. There are various slip theory based formulations in literature which have been named differently based on the selection of sampling planes or static/kinematic constraint imposed to the framework, such as microplane framework from Prat and Bažant (1991) and multi-mechanism from Fang (2003). However, none of the available models can handle the evolving complex anisotropic behaviour of soil.

A detailed formulation of the theory of the multilaminate framework is beyond the scope of this paper, and only the fundamentals used to describe the constitutive implementation will be provided here.

In this paper, a statically constrained, volumetric-deviatoric (VD) split type multilaminate framework has been employed. A total of 33 × 2 sampling planes have been used on which the traction stress vector components are defined as follows:

$${\mathbf{{\boldsymbol \sigma}^{\prime}}}_{i} = \left( {\begin{array}{*{20}c} {\sigma^{\prime}_{n} } \\ \tau \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\sigma^{\prime}_{p,n} + \sigma^{\prime}_{dev,n} } \\ \tau \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {p^{\prime} + {{\varvec{\upsigma}}}^{*} {\mathbf{n}}_{i} {\mathbf{n}}_{i} } \\ {{{\varvec{\upsigma}}}^{*} {\mathbf{n}}_{i} {\mathbf{ - }}\left( {{{\varvec{\upsigma}}}^{*} {\mathbf{n}}_{i} {\mathbf{n}}_{i} } \right){\mathbf{n}}_{i} } \\ \end{array} } \right)$$
(1)

where \({{\varvec\sigma^{\prime}}}_{i}\) is the resultant traction stress vector with local components \(\sigma^{\prime}_{n}\) and \(\tau\), \(\sigma^{\prime}_{dev,n}\) is the magnitude of the deviatoric stress component in the direction normal to the plane, \(\sigma^{\prime}_{p,n} = p^{\prime}\) is the mean effective stress, and \({\mathbf{n}}_{i}\) is the unit normal (or direction cosine) vector.

Fig. 1.
figure 1

Multilaminate description and 3 selected sampling planes out of 33 × 2 planes (a) and their local stress components (b)

Full size image

The stress transformation concept is schematically shown in Fig. 1. Following the transformation process, at each integration point, a locally defined constitutive formulation is executed to calculate micro plastic strains. Then, the plastic contributions from each plane are integrated numerically over the unit sphere given in Fig. 1 to compute its global counterpart as,

$${\mathbf{d\varepsilon }}^{{\mathbf{p}}} = \int\limits_{S} {{\mathbf{T}}_{i} } {\mathbf{d{\boldsymbol \varepsilon} }}_{i}^{p} dS \cong 3 \cdot \sum\limits_{i = 1}^{33} {{\mathbf{T}}_{i} {\mathbf{d{\boldsymbol \varepsilon} }}_{i}^{p} } w_{i}$$
(2)

where \({\mathbf{T}}_{i}\) is the local transformation matrix and \(w_{i}\) is the local weight coefficient.

3 Constitutive Formulations

In this section, an elastoplastic bounding surface plasticity model will be presented. All the formulations are defined on micro level sampling planes unless otherwise stated. The first component of the constitutive model is the yield function. A Mohr-Coulomb type failure criterion has been converted to the yield function by changing the failure envelope to mobilized friction angle, \(\varphi^{\prime}_{mob}\):

$$f = \tau + \sigma^{\prime}_{n} \tan \varphi^{\prime}_{mob} - \frac{{c^{\prime}\tan \varphi^{\prime}_{mob} }}{{\tan \varphi^{\prime}_{cv} }} = 0$$
(3)

The use of Eq. (3) also yields a Mohr-Coulomb type failure shape in global stress space. The evolution of the yield function is controlled by the fabric and plastic strain controlled hyperbolic hardening formulation,

$$\tan \varphi^{\prime}_{mob} = \tan \varphi^{\prime}_{i} + \left( {\tan \varphi^{\prime}_{cv} - \tan \varphi^{\prime}_{i} } \right)\frac{{\varepsilon_{\gamma }^{p} }}{{A + \varepsilon_{\gamma }^{p} }} \cdot f_{d}$$
(4)

where \(\varepsilon_{\gamma }^{p}\) is the micro plastic shear strain, \(\varphi^{\prime}_{i}\) and \(\varphi^{\prime}_{cv}\) define the size of the initial elastic zone from which the mobilization starts and local critical state line (CSL) respectively, and the plastic stiffness parameter \(A\) controls the speed of the mobilization and is formulated as a function of the current state and fabric constant, \(A_{fab}\), i.e.,

$$A = \tan \varphi_{p} \frac{{\sigma^{\prime}_{n} }}{{G_{act} }}\exp \left( { - k_{ani} \cdot A_{fab} } \right)$$
(5)

where the peak friction angle \(\tan \varphi_{p}\) on a contact plane is defined as \(\tan \varphi_{p} = \tan \varphi^{\prime}_{cv} \cdot f_{d}\) and \(G_{act}\) denotes the actual shear modulus which is globally defined in Eq. (8). An exponential parameter \(k_{ani}\) is set to control the influence of fabric on hardening, but for the matter of simplicity set to 1.0 by default in this work. The key ingredient \(f_{d}\) provides the state dependency by including the effect of both current stress and void ratio during the mobilization process, and is given by

$$f_{d} = \psi^{ - \alpha } \,{\text{with}}\,\,\,\psi = \frac{e}{{e_{c} }}\,\,\,\,\,\,{\text{and}}\,\,\,e_{c} = e_{c,0} \exp \left( { - \left( {\frac{{\sigma^{\prime}_{n} }}{{h_{s} }}} \right)^{n} } \right)$$
(6)

where the exponential parameter \(\alpha\) controls the peak friction angle, \(e_{c,0}\) is the critical void ratio at zero stress, and \(h_{s}\) and \(n\) are model parameters describing the location of the CSL in void ratio-effective stress space.

A non-associative flow rule has been employed through the use of the dilatancy formulation proposed by Dafalias and Manzari (2004) to calculate the local normal plastic strain:

$$d\varepsilon_{N}^{p} = d\left| {d\varepsilon_{\gamma }^{p} } \right|\,\,\,\,\,\,\,{\text{with}}\,\,\,\,\,\,d = A_{dila} \left( {\tan \varphi^{\prime}_{cv} \cdot f_{e} - \frac{\tau }{{\sigma^{\prime}_{n} }}} \right)\,\,\,\,\,\,\,\,{\text{and}}\,\,\,\,\,f_{e} = \psi^{\beta }$$
(7)

where \(A_{dila}\) and \(\beta\) are model constants.

Finally, in the elastic part of the model, the hypoelastic formulation proposed by Oztoprak and Bolton (2013) has been used and the current stress and void ratio dependent global actual shear modulus is defined as

$$G_{act} = \frac{{G_{ref} p_{at} }}{{\left( {1 + e} \right)^{3} }}\left( {\frac{{p^{\prime}}}{{p_{at} }}} \right)^{1 - n}$$
(8)

The locally defined constitutive formulations provide independent plastic strain accumulations in different directions, which yields direction dependent hardening and mobilization processes and provides the capability of handling stress induced anisotropy.

4 Anisotropy

In general, constitutive models are calibrated using available experimental data and mostly without considering the fabric effects which can be rarely gathered from common laboratory tests. Even though a single set of critical state parameters can be calibrated to describe the unique, fabric independent critical state behaviour, in the absence of an anisotropic formulation, stress path and orientation dependent hardening behaviour cannot be reproduced using a single set of parameters. The varying hardening behaviour of soil is considered to be the result of the relative orientation of the principal loading direction with respect to the fabric. Omitting the soil fabric misses out the anisotropic nature of the soil and reduces the reliability of the material model parameters which become valid only for the stress path and fabric orientation considered in the calibration procedure.

The commonly used anisotropic critical state theory (ACST) proposed by Li and Dafalias (2012) is a very useful framework to include the anisotropic nature of soil. However, in ACST, in the absence of a fabric evolution formulation, the idea of creating a fabric dependent dilatancy state line (DSL) inevitably deviates the model from CSL. In other words, in ACST, fabric evolution formulation is vital to fill out the premises of critical state theory. Even though the fabric evolution physically exists, its formulation brings additional challenges and requires material parameters which are difficult to measure and calibrate.

In this model, a simple anisotropy formulation has been integrated with the multilaminate framework in a unique way. Unlike the ACST, a fabric independent unique CSL is established without employing a fabric evolution rule. First, a contact force based anisotropic fabric formulation has been employed and a cross anisotropic fabric tensor is defined as

$${\varvec{F}} = F_{norm} \cdot {\varvec{n}}_{F}$$
(9)

in which \(F_{norm} = \left\| {\varvec{F}} \right\|\) is the Euclidian norm of the fabric tensor and \({\varvec{n}}_{F}\) is the fabric orientation. Then, in order to convert the above defined tensorial quantity \({\varvec{F}}\) to a scalar quantity \(A_{fab}\) which can be used to modify constitutive formulations, the direction of local deviator stress vector has been used as

$$A_{fab} = {\varvec{F}}:{\varvec{n}}_{i}^{dev} = F_{norm} \left( {{\varvec{n}}_{F} :{\varvec{n}}_{i}^{dev} } \right)$$
(10)

where \({\varvec{n}}_{i}^{dev}\) is the local unit deviator stress vector. The scalar constant \(A_{fab}\) is used to the modify the hardening modulus in Eq. (5) and the exponential parameters controlling the hardening and dilatancy formulations in Eqs. (6) and (7) such that,

$$\alpha = \left\langle {\alpha_{i} + A_{fab} } \right\rangle \,\,\,\,{\text{and}}\,\,\,\,\beta = \left\langle {\beta_{i} + A_{fab} } \right\rangle$$
(11)

Following the update given in Eq. (11), the \(f_{d}\) and \(f_{e}\) formulations are modified as follows:

$$f_{d} = \psi^{{ - \left\langle {\alpha_{i} + A_{fab} } \right\rangle }} \,\,\,\,{\text{and}}\,\,\,\,\,f_{e} = \psi^{{\left\langle {\beta_{i} + A_{fab} } \right\rangle }}$$
(12)

Together with above given change, the hardening and dilatancy behaviours of soil become fabric dependent. Unlike the other ACST based formulations available in literature, the proposed model yields different fabric constants in different directions, depending on the evolution of the local deviator stress vector. Finally, at the critical state, when the current void ratio \(e\) reaches the critical void ratio \(e_{c}\), independent from the exponential fabric terms in Eq. (12), \(\psi\) becomes unconditionally equal to 1.0.

5 Simulations and Comparison

In this section, the simulation performance of the proposed model has been compared with two advanced constitutive models: Sanisand, developed by Dafalias and Manzari (2004) and hypoplasticity with intergranular strain, proposed by Niemunis and Herle (1997). The set of parameters calibrated for Karlsruhe fine sand for the proposed model is listed in Table 1. No calibration has been carried out for the Sanisand and hypoplasticity models; instead, the available sets of parameters provided in Wichtmann (2016) have been used. Moreover, the experimental database provided by Wichtmann (2016) has been used in the following comparisons, and the experimental data labels are adopted from the database (i.e. TMD, TMU). In the following comparisons, experimental data, proposed model, hypoplasticity and Sanisand have been denoted by black, red, green and purple colours, respectively.

Table 1. Material parameters of proposed constitutive model for Karlsruhe fine sand
Full size table

In the first comparison provided in Fig. 2, loose, medium dense and dense samples are simulated. The increase in peak deviator stress with increasing initial relative density is well captured by Sanisand and the proposed model. In Fig. 3, samples with similar initial densities consolidated under different cell pressures are simulated. As expected, higher confining pressure suppresses the dilation. Compared to Sanisand and the proposed model, hypoplasticity has a clear disadvantage in predicting volumetric behaviour, both in Figs. 2 and 3. The main reason is that the inherent volumetric/shear coupling in hypoplasticity does not provide a desirable independent control over the dilatancy. In other words, unlike the proposed model where \(A_{dila}\) and \(\beta\) are explicitly calibrated to capture volumetric behaviour, hypoplasticity does not provide a specific parameter for a direct control over the volumetric behaviour.

Fig. 2.
figure 2

Simulations of drained triaxial tests with different initial densities all consolidated at 100 kPa

Full size image
Fig. 3.
figure 3

Simulations of drained triaxial tests on medium dense samples (0.57 ≤ Dr,0 ≤ 0.68) with different initial pressures

Full size image
Fig. 4.
figure 4

Simulations of undrained triaxial compression and extension tests with different initial densities

Full size image

In undrained simulations, the proposed model provides the best prediction for various initial densities and loading directions. Even though all three models show general agreement with the experimental results in Fig. 4, Sanisand and hypoplasticity fail to reproduce the p’-q stress paths on the extension side and show a poor reproduction of the development of pore water pressure. Finally, the comparison of the compression and extension tests reveals the influence of the missing fabric formulation in hypoplasticity and Sanisand which results in higher deviator stresses and less contractive behaviour.

6 Conclusion

In this work, a new semi-micromechanical constitutive formulation for anisotropic sands has been described and its performance is compared with two other commonly used models, namely Sanisand and hypoplasticity with intergranular strain. The inherent capabilities of the multilaminate framework enable the model to simulate the influence of stress induced anisotropy. In this work, the framework is further enhanced by incorporating ACST to handle evolving fabric anisotropy. A unique fabric evolution formulation providing varying fabric evolution is provided. Unlike the available ACST based models where the fabric tensor converted to a single scalar value, a direction dependent fabric evolution rule has been defined.