Rotorcraft Control Systems

Abstract

This chapter provides an overview of flight control systems for rotorcraft at an introductory level. There exist many rotorcraft configurations, however, we will focus our attention on conventional helicopters to provide a fundamental understanding. We will cover standard and advanced control design methods to design and validate flight control algorithms for both stability augmentation and autopilot systems. We will touch on some essential elements of feedback control theory before showing how the design methods are implemented. A key characteristic of the discussed design methods is that they are suitable for multivariable systems, which offer advantages for minimising key helicopter dynamic couplings. The control design methods also offer improved robustness properties leading to flight envelope protection characteristics. We will cover key metrics to assess the robustness and performance properties of the flight control laws from a control theory approach. These control laws form the basis for the assessment of the flight control laws in terms of handling qualities.

Nomenclature  

BIBO:

Bounded-Input Bounded-Output

LQR:

Linear Quadratic Regulator

LTI:

Linear Time-Invariant

MIMO:

Multiple-Input Multiple-Output

PID:

Proportional-Integral-Derivative

SISO:

Single-Input Single-Output

A, B, C, D:

Matrix coefficients of state-space representations

F:

Output feedback gain matrix

H:

State feedback gain matrix

I:

Identity matrix with adequate dimensions

G:

Plant

K:

Compensator

G(s):

Plant transfer function

K(s):

Controller transfer function

S(s):

Sensitivity transfer function

T(s):

Co-sensitivity transfer function

$w_p(s)$:

Sensitivity weight

$w_{KS}(s)$:

Control actions weight

$w_T(s)$:

Co-sensitivity weight

$k_p, k_i, k_D, N$:

PID controller parameters

$S_o^*,M,\upomega _S^*$:

Sensitivity weight parameters

$\upomega _T^*, N_T, \upgamma _T$:

Co-sensitivity weight parameters

$w_{KS}$:

Control actions constant parameter

j:

Imaginary unit

l:

Number of outputs

m:

Number of inputs

n:

Number of states

s:

Laplace variable

t:

Time (s)

T:

Transpose operator

c(t):

Command or reference signal

e(t):

Error signal

n(t):

Noise signal

u(t):

Control actions

x(t):

State vector signal

y(t):

Output signal

$\overline{\upsigma }(.)$:

Largest singular value

$\underline{\upsigma }(.)$:

Lowest singular value

$\upomega$:

frequency variable (rad/s)

$\upomega _S$:

Sensitivity bandwidth (rad/s)

$\upomega _T$:

Co-sensitivity bandwidth (rad/s)

$\Vert . \Vert _{\infty }$:

Infinity norm

 

7.1 Feedback Control

In the context of engineering systems, the fundamental objective of feedback control is to regulate flight variables of interest and de-sensitise the rotorcraft dynamics to key parameter variations (e.g. changes in centre of gravity, aerodynamic coefficients, etc.). Regulation of key aircraft flight variables (attitude and velocities) are related to pilot command tracking and alleviation of gust perturbations as well. There are three main characteristics when looking at the design of flight control systems:

• Stabilisation: This property is concerned with the ability to stabilise the dynamics of the rotorcraft. A primary role of using feedback in flight control systems is to stabilise rotorcraft flight dynamics and/or improve the original rotorcraft transient response. This is one of the main roles of the subsystem known as stability augmentation.

• Performance: The performance of the flight control systems is measured with respect to the ability to track pilot command signals and provide disturbance rejection capabilities. These two properties can be assessed separately. There are a number of key metrics developed to assess the quality of the performance, both in the time- and the frequency-domain. This is one of the main roles of the flight control subsystem known as autopilot or autonomous system.

• Robustness: This property is concerned with the ability of the control algorithm to maintain stability and certain level of performance despite variations on the rotorcraft aeromechanics. In control theory, this property is further split into robust stability and robust performance but we will consider only robust stability in this chapter to simplify the discussions [1]. Although robust stability might not get much attention in flight dynamics textbooks, robust stability is of paramount importance to flight control because of its impact on the airworthiness and certification requirements of the aircraft.

The afore-mentioned characteristics provide great benefits in terms of pilot work load alleviation, which in turn also has an impact on improving the safety of operations. Given significant progress in the areas of Artificial Intelligence and Machine Learning methods [2], there has been an increased interest recently to apply these methods to replace key pilot tasks, such as obstacle avoidance and trajectory planning. In the aerospace community these properties are referred as autonomy. Autonomy algorithms are outside the scope of this chapter but note that their performance is strongly dependent on the performance and reliability of the flight control systems we discuss in this chapter.

The afore-mentioned qualities are achieved in flight control systems using feedback loops, with the elementary representation shown in Fig. 7.1. This feedback loop shows the special interconnection of two systems: G represents the system to control and the controller K. The flight variables of interest are collected in the vector signal y(t). Measurements of the output signal is represented by $y_m(t)$ after the presence of measurement noise n(t) has been included. The difference between commands c(t) and the measured control signal $y_m(t)$ is then fed into a compensator K or algorithm to process or dictate the various control signals represented by u(t) to perform the control task. In this diagram note that the signal d(t) accounts for external disturbances, which for autopilot applications, accounts for gusts disturbances typically.

Fig. 7.1

Feedback interconnection

Fig. 7.2

Standard architecture for flight control systems

 Flight control systems exploit the benefits of feedback and use a nested configuration for stability augmentation and pilot command tracking tasks, see Fig. 7.2. The inner feedback loop, known as stability augmentation, is included to provide improved flight dynamics. These are required for instance if the lateral and longitudinal dynamics of the original aircraft are either unstable or provide poor transient response (low-damped modes and/or slow responses). Improving the flight dynamics of the rotorcraft facilitates the design and enables achieving a desired performance for pilot command tracking purposes. This is the main purpose of this outer loop control system, also known as the autopilot system. The performance is assessed mainly in terms of tracking and disturbance rejection capabilities, which are connected to handling quality requirements.

7.2 Flight Dynamic Models for Rotorcraft Flight Control Design

 Rotorcraft flight dynamics obtained from first principles are complex (high-order and nonlinear) and in most cases not suitable for standard control system design methods. For this reason, available models, which are usually obtained following first principle models [3], need to be approximated to a linear form to facilitate the design of the flight control algorithms. These linear representations are only valid for very specific points of the flight envelope and obtained at trimmed (equilibrium) conditions. Linear models hence provide a local description of the aircraft behaviour around a chosen equilibrium position. For instance, for conventional helicopter, the main flight conditions are hover, vertical motion, longitudinal and lateral flight, trimmed at different airspeeds. Multiple linearisation is required to obtain a simplified and comprehensive, yet meaningful, picture of the rotorcraft behaviour.

Simplified rotorcraft flight dynamics models are expressed as a Linear-Time-Invariant (LTI) system. LTI systems can be represented as either a transfer function matrix, typically denoted as G(s), or alternatively, as a state-space representation

$$\begin{aligned} G \sim \left\{ \begin{array}{ll} x(t) = A x(t) + B u(t), \quad x(0) \in \mathbb {R}^n \\ y(t) = C x(t) + D u(t) \end{array} \right. \end{aligned}$$

(7.1)

The coefficient n denotes the number of states required to represent the rotorcraft flight dynamics and represents also the dimension of the vector signal (in column form) x(t). The number of available measured outputs is l and represents also the dimension of the output signal y(t). The number of control inputs to operate the rotorcraft is m which is also the dimension of the vector signal u(t). The matrix coefficients of the model are constant and their dimensions are $A \in \mathbb {R}^{n \times n}, B \in \mathbb {R}^{n \times m}, C \in \mathbb {R}^{l \times n}$ and $D \in \mathbb {R}^{l \times m}$. Typically, y(t) contains a subset of the signals in x(t) and hence $l < n$ and $D=0$.

A very important relation that connects the transfer function and state-variable representations is

$$\begin{aligned} G(s) = C(sI -A)^{-1}B + D \end{aligned}$$

(7.2)

A key concept in control theory on whether a state-space representation is totally equivalent to the transfer function matrix representation shown above is associated with more fundamental concepts known as controllability and observability. To simplify the discussions in this chapter, we will assume that any obtained flight dynamic model represented in state-space form is both controllable and observable. This assumption also applies for the representation of the controller K. For more information on these concepts, refer to [1].  

Another important concept associated with LTI systems is stability. Stability of LTI systems can be considered from two points of views - the quality of the free and forced response. Stability of the free response (zero inputs) is considered for non-zero initial conditions and analysed via state-space representations typically. Loosely speaking, we say the free response is stable if the state vector (and hence the output) remain finite at all times and converge to zero. This stability notion is known as asymptotic stability. On the other hand, stability of the forced response (zero initial conditions) is considered via transfer function representations. Loosely speaking, we say that the forced response is stable if finite input signals leads to finite output signals. This stability concept is referred to as Bounded-Input Bounded-Output (BIBO) stability.Asymptotic stability is obtained if the eigenvalues of the matrix A have negative real part. For transfer functions, BIBO stability is obtained if all the roots of the denominator of the matrix G(s) have negative real part. For LTI representations which are controllable and observable, the roots of the denominator of G(s) are the same as the eigenvalues of the state matrix A. Therefore we can claim that these two stability notions are equivalent in the sense that the same condition must hold to ensure both types of stability. These stability conditions are necessary and sufficient meaning that if they are not satisfied, then the LTI system do not meet the definitions of asymptotic and BIBO stability [4].

Table 7.1 Typical state-vector and control elements in conventional helicopters

Table 7.2 Control inputs in conventional helicopters

 Typically for conventional helicopters, the state vector contains the signals shown in Table 7.1 and the control inputs are shown in Table 7.2. Note that the adopted notation for the linear velocities is different from the more standard notation found on flight dynamics textbooks to avoid confusion with the notation implemented to represent signals in the feedback loop.

Rotorcraft flight dynamics are usually separated into longitudinal and lateral dynamics when performing dynamic stability analysis and flight control design [3, 5].Longitudinal dynamics consider the pitch and vertical motion of the rotorcraft, while lateral dynamics are concerned with the yaw or directional motion and the rolling behaviour. This separation might not be valid for all rotorcraft configurations and hence a more comprehensive multivariable model that models cross-couplings between these two dynamics would be required to design a more effective flight control system at minimising undesired couplings.

7.3 Stability, Robustness and Performance of Feedback Control Systems

7.3.1 Feedback Stability

The primary property to assess in any feedback control system is its stability. To simplify the discussions, we will assume that both the compensator K and the plant G can be represented by LTI elements reliably. Feedback stability refers to the values of the signal at any location in the feedback loop remaining finite in the presence of finite exogenous signals (c(t), d(t), n(t)). For this reason it is necessary to look at various transfer functions obtained from all possible pairs of inputs and outputs in the feedback loop. A sufficient and necessary condition for stability of the feedback loop is simplified by testing for stability of the following transfer functions

$$\begin{aligned} (I+K(s)G(s))^{-1} \end{aligned}$$

(7.3)

$$\begin{aligned} K(s)(I+G(s)K(s))^{-1} \end{aligned}$$

(7.4)

$$\begin{aligned} G(s)(I+K(s)G(s))^{-1}\end{aligned}$$

(7.5)

$$\begin{aligned} (I+G(s)K(s))^{-1} \end{aligned}$$

(7.6)

Refer to [1] for more details. A more elaborate and general condition for feedback stability can also be found in  [6], which is expressed in terms of state-space representations for G and K. Feedback systems with this property are called internally stable and this stability test should be verified before performing any performance assessment of the flight control system.

7.3.2 Feedback Robustness

 Stability alone is not enough in rotorcraft control system design mainly because LTI models can only capture the dynamics of the rotorcraft up to some extent and rotorcraft dynamics are also subject to variations. For this reason, we are interested in determining somehow how tolerant the feedback loop is to certain variations in the flight control system. There are two main metrics that are widely used for this purpose - they are the Gain Margin (GM) and Phase Margin (PM). These metrics are derived from the well-known Nyquist Stability Criterion [4] but these metrics are applicable only to single-input single-output feedback systems, i.e., when both G and K have one input and one output and both are stable in most cases.GM accounts for gain variations in G typically and this metric indicates how much the gain can be increased before the feedback loop become unstable. A typical design requirement for feedback systems is

$$\begin{aligned} \text {GM} \ge 2 \end{aligned}$$

(7.7)

 The PM is associated instead with time delays expressed in the form of phase-lag. Delays are expected to occur in the communication channel between the controller and any actuators primarily and latency from on-board sensors. The PM indicates how much phase lag can exist before the system becomes unstable. A typical design requirement is

$$\begin{aligned} \text {PM} \ge 30^\circ \end{aligned}$$

(7.8)

GM and PM are not always reliable since they account for individual changes in gain and delays, but not combined or simultaneous variations. For this reason a less known and very useful criterion is provided in terms of a metric known as the peak sensitivity. The Sensitivity transfer function S(s) of the feedback loop is defined as

$$\begin{aligned} S(s) = (I + G(s)K(s))^{-1} \end{aligned}$$

(7.9)

Loosely speaking, the largest gain of this sensitivity when evaluated in the frequency domain is indicated by

$$\begin{aligned} \Vert S \Vert _{\infty } = \max _\upomega |S(j \upomega )|, \forall \upomega \end{aligned}$$

(7.10)

 This value is also known as the H-infinity norm of the Sensitivity. The reasons for this particular notation is outside the scope of this manuscript, however, for those interested Readers, they can refer to the mathematical field of Functional Analysis [7]. A typical robustness condition in terms of the peak sensitivity is

$$\begin{aligned} \Vert S \Vert _\infty \le 2 \end{aligned}$$

(7.11)

For multivariable systems, a metric for robustness can be obtained from the multivariable Nyquist criterion. Note that the stability condition of the closed-loop can be expressed in the frequency domain as follows

$$\begin{aligned} \text {det}(I + G(j\upomega )K(j\upomega )) \ne 0, \forall \upomega \end{aligned}$$

(7.12)

and for stable G(s) and K(s). This means that the plot of $\text {det}(I + G(j\upomega )K(j\upomega ))$ must not enclose the origin to ensure stability. The robustness metric can then be obtained by making sure the plot do not pass too close to the origin of the complex plane. A similar metric derived from the peak sensitivity mentioned above could be established by making sure the closest point to the origin is larger than 0.5

$$\begin{aligned} | \text {det}(I + G(j\upomega )K(j\upomega )) | \ge 0.5, \forall \upomega \end{aligned}$$

(7.13)

Clearly the more the above conditions are exceeded, the more robust the flight control system is. However, the conflicting nature between performance and robustness is well-know in feedback systems and the task of the control design engineer is to achieve a desired trade-off. For practical flight control systems where the feedback loops are SISO, it is recommended to use the three aforementioned metrics (GM, PM and $\Vert S \Vert _\infty$) whenever applicable. The metrics can be easily calculated with commercial software such as Matlab.

7.3.3 Performance Assessment: Time-domain

A pragmatic approach to evaluate the performance of the control system system is by simulating the responses to step command and disturbance signals and in the presence of white noise. This approach is particularly important to assess the transient characteristics of the flight control system. For LTI feedback systems, the analysis can be done separately due to the superposition principle that governs LTI systems but this is not the case if the controller is implemented on more comprehensive nonlinear models. When considering step responses, there are well known metrics, such as overshoot, rise time, steady-state error and settling time, that should be used when assessing such responses [4]. These metrics are introduced usually to inspect the tracking characteristics of control systems in most textbooks but they can be applied also to assess the disturbance rejection characteristics of the control system [4].

Apart from step signals, the control system should be tested against all possible signal forms according to the considered application. The performance assessment should also include the effects of measurement noise which is usually simulated by using white noise signals in n(t). Also, any time-domain simulations should inspect the control signal u(t) to make sure it complies with actuators operational capabilities. All these aspects are very important and they all should be tested in any simulation campaign very carefully and extensively. The more comprehensive the assessment of the control system is under simulation environments, the more confidence is gained before the system is tried on practical implementations.

7.3.4 Performance Assessment: Frequency-Domain

The performance of feedback control systems should also be assessed in the frequency domain because the information is richer and more comprehensive than in the time-domain. Assessment in the frequency domain is particularly important to assess the performance at steady-state. For this purpose, note that the feedback loop depicted in Fig. 7.1 can be described by the following relations

$$\begin{aligned} y(s)= & {} T(s) c(s) + S(s) d(s) + T(s) n(s) \end{aligned}$$

(7.14)

$$\begin{aligned} e(s)= & {} c(s) - y(s) = -S(s) c(s) + S(s) d(s) - T(s)n(s) \end{aligned}$$

(7.15)

$$\begin{aligned} u(s)= & {} K(s)S(s) (c(s) - d(s) - n(s)) \end{aligned}$$

(7.16)

Note that the above expressions are expressed in terms of two especial transfer functions: (i) the Sensitivity S(s) defined in (7.9) and (ii) the Complementary Sensitivity or co-sensitivity T(s) defined as follows

$$\begin{aligned} T(s) = G(s)K(s)(I+G(s)K(s))^{-1} \end{aligned}$$

(7.17)

The response of the output to command signals and noise is determined by T(s) and hence this is the transfer function to assess for pilot command tracking tasks if perturbations are not significant. On the other hand, the effect of external disturbances on the output and the error signal is captured by the Sensitivity transfer function S(s). The response of the control actions u(t) due to the presence command, perturbations and noise are dictated by K(s)S(s). Therefore these three transfer functions play a key a role in the performance of the flight control system and all of them should be assessed very carefully when validating any control strategy.

The more general way to assess the performance is by inspecting the singular values [8] of the transfer functions in the frequency domain. $\upsigma (S(j\upomega ))$ denotes the singular value of the complex matrix $S(j\upomega )$. A similar notation follows for $\upsigma (T(j\upomega ))$ and $\upsigma (K(j\upomega )S(j\upomega ))$. The smallest and largest singular values are denoted by $\underline{\upsigma }(.)$ and $\overline{\upsigma }(.)$, respectively. The singular value plot for a transfer function matrix plots the singular values across all frequencies. This plot can be obtained with the commercial software Matlab using the command sigma. There are key parameters flight control design engineers should take into account when assessing the performance in the frequency domain. We bring our attention to the following metrics:  

Sensitivity bandwidth.:

 This parameter is denoted by $\upomega _S$ and it is expressed in rad/s usually. This metric is obtained by the frequency at which the largest singular value of $S(j\upomega )$ crosses -3 dB from below

$$ \overline{\upsigma }(S(j \upomega _S) )= \frac{1}{\sqrt{2}} \approx 0.707$$

This metric can be considered as the closed-loop bandwidth, and it provides a metric of the largest frequency component in the disturbance signal d(t) for which satisfactory attenuation is achieved. This is also the largest frequency at which the error signal $c(t)-y(t)$ is reduced satisfactorily. It is therefore expected that for any disturbance containing frequency elements above this value, the disturbance rejection and the error between the command signal and the controlled variable become poor.

Peak Sensitivity.:

 Recall that this metric $\Vert S \Vert _\infty$ was already introduced earlier as a robustness parameter for SISO systems. For MIMO system, the peak sensitivity becomes the maximum of the largest singular value of the Sensitivity across all frequencies

$$\begin{aligned} \Vert S \Vert _\infty = \max _\upomega \overline{\upsigma }(S(j\upomega )) \end{aligned}$$

(7.18)

This metric represents a measurement of the worst-case gain when performing disturbance rejection. Clearly, we would like to have this value as low as possible.

Sensitivity Low-frequency Gain.:

 This metric represents the worst gain expected when providing disturbance rejection to constant signals and we will denote it as

$$\begin{aligned} S_0 = \overline{\upsigma }(S(j0)) \end{aligned}$$

(7.19)

In flight control examples, this metric would be related to the the capabilities of the flight control system to reject constant gusts. We would like to design the flight control system to achieve as low a value as possible of $S_0$.

Co-sensitivity bandwidth.:

This parameter is denoted by $\upomega _T$ and is defined when the lowest singular value of $T(j\upomega )$ crosses -3 dB from above

$$\begin{aligned} \underline{\upsigma }(T(j \upomega _T) )= \frac{1}{\sqrt{2}} \approx 0.707 \end{aligned}$$

(7.20)

This metric indicates the maximum frequency component in the command signals for which satisfactory tracking is achieved. Note that this metric is only concerned with tracking of the amplitude for command signals, but does not incorporate information about the quality of phase tracking. For this reason this definition of bandwidth can be misleading. For example, consider the SISO case where the singular value becomes $|T(j\upomega )|$. We can have a metric of bandwidth obtained at $|T(j\upomega _T)| \approx -3$ dB, but on the other hand having a poor phase tracking (for instance $\angle T(j\upomega _T) \ge 30^\circ$). In this case the tracking of the harmonic command signal would be poor because of the noticeable phase difference between the output and command signals, and a more reliable bandwidth metric would have a much lower value than the bandwidth measurement provided by the above definition.

 

7.4 Control Design for Flight Control

There exist a plethora of control design methods with particular benefits depending on the requirements of the application. We will discuss in this section a selected combination of conventional and more recent design methods given the benefits they bring to the design of both stability augmentation and autopilot systems in flight control system design.

7.4.1 Stability Augmentation

The main purpose of control design for stability augmentation is the improvement of the rotorcraft dynamics by the use of feedback. Rotorcraft dynamic are adjusted depending on the desired degree of rotorcraft stability. A common approach is to use feedback to relocate key rotorcraft modes into desired locations, thus improving their transient characteristics by typically making them more stable, (negative real part being larger in absolute value), reducing the damping (reducing their imaginary part or making their locations closer to the real axis) and stabilising unstable modes (moving these poles into the left-half side of the complex plane). Two common strategies for these two goals are Root Locus and Pole Placement [4]. While Root Locus is particularly useful for SISO control system design, Pole Placement is more general and suitable for MIMO systems.

Stability augmentation can be achieved typically by feeding the attitude rates and using these measurements for pole placement. The method relies on manipulation of the state-space description and makes full use of appropriate computational tools. Its real application is limited by the assumption that reliable measurements or estimations of the state-variables are available. The unaugmented or open-loop rotorcraft dynamics are expressed in the standard state-representation (7.1). The pole relocation is implemented by means of a full-state feedback law expressed in the form of a linear combination of the states

$$\begin{aligned} u(t) = v(t) - H x(t) \end{aligned}$$

(7.21)

 The feedback gain matrix $H \in \mathbb {R}^{m \times n}$ determines the location of the closed-loop and is the parameter to choose. The new input signal v(t) is the input to the augmented system and is the new input used later on for the autopilot design task. The above control law leads to the following closed-loop or augmented state-space representation

$$\begin{aligned} \dot{x}(t)= & {} (A - BH) x(t) + B v(t) \end{aligned}$$

(7.22)

$$\begin{aligned} y(t)= & {} (C - DH) x(t) + D v(t) \end{aligned}$$

(7.23)

There exist computational tools such as Matlab (see command place) whereby the user provides the values of A, B and the desired closed-loop pole locations in vector form so the eigenvalues of the closed-loop matrix $A-BH$ match the desired modes. The command will return the numerical values of H. There are certain requirements on A and B for the strategy to work, such as the pair A and B being a controllable pair, the number of closed-loop poles must be the same as n and no re-located eigenvalue should have a multiplicity greater than the number of inputs [1].In many rotorcraft applications the output signal y(t) is a subset of the elements in x(t), leading to a zero matrix D. The pole placement approach can be implemented via Output feedback in these cases in a simple form. Note the control law becomes instead

$$\begin{aligned} u(t) = v(t) - F y(t) \end{aligned}$$

(7.24)

leading to the following closed-loop description

$$\begin{aligned} \dot{x}(t)= & {} (A - BH) x(t) + B v(t) \end{aligned}$$

(7.25)

$$\begin{aligned} y(t)= & {} C x(t) \end{aligned}$$

(7.26)

with

$$\begin{aligned} H = F C \end{aligned}$$

(7.27)

The pole placement can be implemented by using the original matrices A, B and specifying the desired closed-loop locations to obtain H as explained earlier. The gain matrix F can be obtained as follows

$$\begin{aligned} F = H C^{\dagger } \end{aligned}$$

(7.28)

whereby $C^{\dagger } = C^T (C C^T)^{-1}$ represents the pseudo-inverse of C.

7.4.2 Autopilot System

Recall the outer-loop of the flight control system provides autopilot characteristics enabling the pilot to execute certain manoeuvres under automatic control. The autopilot system controls the rotorcraft motion via the regulation of the rotorcraft attitude. Even basic automation capabilities might look limited compared with more advanced autonomy algorithms, yet autopilot systems reduce pilot workload significantly. A common approach to tune SISO control systems is Proportional-Integral-Derivative (PID) control for the tracking of the attitude. The control law following PID principles is implemented in practice typically as

$$\begin{aligned} K(s) = k_p + \frac{k_i}{s} + \frac{k_d s}{Ns + 1} \end{aligned}$$

(7.29)

The controller parameters are $k_p, k_i, k_d$ and N. The controller in this case will provide the actions in terms of the new control input v(t) introduced by the stability augmentation system.

A design approach suitable to rotorcraft flight control when dynamic couplings are significant and can not be addressed by the stability augmentation system are based on state-space methods and the more recent Robust Control methods. A popular approach known as Linear Quadratic Regulator (LQR) could be implemented to handle the challenges caused by the multivariable control design problem. However, these controllers rely on accurate estimation or measurements of the states (not only the attitude angles) and these controllers are criticised for a lack of robustness [9]. We explore a more recent design strategy which are based on the principle of shaping key closed-loop transfer functions to achieve a desired level of robustness and performance. The particular design approach that we will consider is covered under the umbrella of Robust Control methods, which are also known as $\mathcal {H}_\infty$ control. The design methodologies rely on advanced optimisation algorithms to obtain the control laws but the design procedures of the controllers are rather transparent to the design engineer without the need to know the intricacies of the optimisation routines.Mixed-Sensitivity Robust Control aims to shape the frequency response of three key transfer functions: the Sensivity S(s), the Co-Sensitivity T(s) and K(s)S(s) which accounts for the control actions. The principles are based on using transfer function weights to dictate the desired shape.

Recall that the lower the values of $\overline{\upsigma }(S(j \upomega ))$, the better characteristics in terms of disturbance rejection and error reduction. It is therefore natural to indicate the desired shape of the Sensitivity by setting an upper bound on desired vales across frequencies. Mathematically, we can express this as

$$\begin{aligned} \overline{\upsigma }(S(j \upomega )) < |w_p(j\upomega )|^{-1}, \quad \forall \upomega \end{aligned}$$

(7.30)

The inverse on the transfer function on the right hand side is introduced for mathematical convenience, and $w_p(s)$ in this case is considered as a SISO transfer function to facilitate the discussions. The above inequality can be equivalently expressed in terms of a weighted Sensitivity

$$\begin{aligned} \Vert w_p S \Vert _\infty < 1 \end{aligned}$$

(7.31)

A common choice for $w_p(s)$ provides large gain inside the desired control bandwidth to demand low sensitvity gains

$$\begin{aligned} w_p(s) = \frac{s/M + \upomega _S^*}{s+S_0^* \upomega _S^*} \end{aligned}$$

(7.32)

The parameters could be chosen for instance to prescribe design requirements, such as

$$\begin{aligned} S_0^*\le & {} \text {Desired worst-case steady-state error}\\ M\le & {} \text {Desired worst-case disturbance rejection gain} \\ \upomega _S^*\ge & {} \text {Desired minimum bandwidth (rad/s) } \end{aligned}$$

The condition to shape the frequency response for the control actions transfer function K(s)S(s) is as follows

$$\begin{aligned} \Vert w_{KS} KS \Vert _\infty < 1 \end{aligned}$$

(7.33)

In many cases, a simple constant weight can be chosen to determine the desired largest control actions given largest amplitude values of the exogenous signals (c(t), d(t) and n(t)). For instance, in the SISO case and considering only the effects of command signals, the weight can be chosen as

$$\begin{aligned} {\bar{u}} \le w_{KS}^{-1} \bar{c} \end{aligned}$$

(7.34)

with $\bar{u}$ and $\bar{c}$ representing the desired largest absolute control input amplitude and the expected largest command amplitude value, respectively. Note that the above inequality holds only for steady-state values and hence the constraint on the control input at every time instant is not guaranteed but it can be used as an initial choosing value for $w_{KS}$.

The same principles can be applied to shape the co-sensitivity T(s) via a performance weight $w_T(s)$

$$\begin{aligned} \Vert w_T T \Vert _\infty < 1 \end{aligned}$$

(7.35)

Typically the weight offer large gain outside the bandwidth region to ensure good noise attenuation and also to provide good robustness characteristics [1] . A weight that meets these specifications has the following structure

$$\begin{aligned} w_T(s) = \upgamma _T \frac{ s + \upomega _T^*}{s + N_T \upomega _T^*} \end{aligned}$$

(7.36)

with

$$\begin{aligned} \upomega _T^*\ge & {} \text {Maximum frequency at which dynamic model is considered reliable}\\ N_T> & {} 1 \\ \upgamma _T\ge & {} \text {Amount of relative uncertainty at high frequencies} \end{aligned}$$

In many applications, the control design are based on shaping the frequency responses of S(s) and K(s)S(s) only, providing very good design results. The control Engineer can use computational tools such as those found in the Robust Control Toolbox in Matlab to be able to obtain the controllers which satisfy one or more of the above specification requirements. The Matlab command to perform mixed-sensitivity control design is mixsyn. There are many more mathematical details which are not discussed in this chapter around this control design philosophy but the Reader is referred to [1] for a comprehensive source on robust control methods. The main appeal of the above methods in comparison with more traditional approaches, such as PID, is that there is a more transparent relation between the controller parameters, performance and robustness specifications and a desired trade-off. We will demonstrate the aforementioned design strategies with a numerical example shown in the next section.

7.5 Rotorcraft Flight Control System Design—Numerical Example

For this example, we will use the helicopter model found in Matlab under the title “Multi-loop controller of a helicopter”. This example uses an eight-state helicopter model at the hovering trim condition. The model is presented in state-space form, with the state vector having the same signals shown in Table 7.1 arranged as follows

$$\begin{aligned} x(t) = [v_x(t), v_z(t), q(t), \theta (t), v_y(t), p(t), \phi (t), r(t)]^T \end{aligned}$$

(7.37)

In this example, the linear velocity are expressed in m/s. Attitude angles and rates are expressed in deg and deg/s, respectively. The control inputs in this example are the longitudinal and lateral cyclic, as well as the tail rotor

$$\begin{aligned} u(t) = [u_{long}(t), u_{lat}(t), u_{tail}(t)]^T \end{aligned}$$

(7.38)

The command signals are expressed in degrees. The values of the state-space model are as follows

$$\begin{aligned} A= & {} \begin{bmatrix} -0.0191 &{}0.0170 &{} 0.3839 &{}-9.7924 &{}-0.0008 &{}-0.3371 &{}0 &{}0 \\ 0.0136 &{}-0.2994 &{} 0.0237 &{}-0.5859 &{}-0.0017 &{}-0.0257 &{}0.5374 &{}0\\ 0.0405 &{}-0.0026 &{}-1.8394 &{} 0 &{}0 .0024 &{} 0.5281 &{}0 &{}-0.0015 \\ 0 &{}0 &{}0.9985 &{}0 &{}0 &{}0 &{}0 &{}0.0549 \\ 0.0010 &{}-0.0017 &{}-0.3381 &{}0.0322 &{}-0.0349 &{}-0.4032 &{}9.7777 &{}0.1168\\ 0.0130 &{}0 &{}-3.047 &{}0 &{}-0.229 &{}-10.6199 &{}0 &{}-0.0333\\ 0 &{}0 &{}-0.0033 &{}0 &{}0 &{}1 &{}0 &{}0.0598\\ 0.0020 &{}0.0060 &{}-0.5412 &{}0 &{}0.0039 &{}-1.8554 &{}0 &{}-0.3487 \end{bmatrix}\\ \\ B= & {} \begin{bmatrix} -10.3456 &{} 1.0793 &{}0\\ -0.7293 &{}0.0755 &{}0\\ 27.0900 &{}-4.7239 &{}-0.1857\\ 0 &{}0 &{}0\\ -1.0820 &{}-10.3713 &{}4.7239\\ -27.2884 &{}-156.4425 &{}-1.0690\\ 0 &{}0 &{}0\\ -4.8969 &{}-27.9728 &{}-12.9304 \end{bmatrix}, C = \begin{bmatrix} 0 &{}0 &{}0 &{}1 &{}0 &{}0 &{}0 &{}0\\ 0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}1 &{}0\\ 0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}0 &{}1\\ 0 &{}0 &{}1 &{}0 &{}0 &{}0 &{}0 &{}0\\ 0 &{}0 &{}0 &{}0 &{}0 &{}1 &{}0 &{}0 \end{bmatrix}, D = 0_{5\times 3} \end{aligned}$$

Fig. 7.3

Simulink simulation diagram

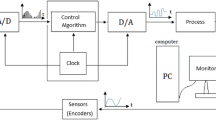
The implementation of the flight control system is shown in Fig. 7.3. Note that both systems implement the same stability augmentation but simulates two different autopilot designs: PID and the Robust Control referred as H-infinity. The original example includes roll-off filters with cut-off at 40 rad/s to partially limit the control bandwidth and safeguard against neglected high-frequency rotor dynamics. To facilitate the control design discussions, these low-pass filters are neglected in the control design discussed below. The low-pass filters are required mostly for practical implementations and their presence is expected to not make much difference at the control design stage. Finally, we have modified the simulations by adding output disturbance signals at the output to assess the disturbance rejection capabilities of the system.

7.5.1 Stability Augmentation

Examining the eigenvalues of A, we can observe that the pair $0.0544 \pm j0.4415$ is not stable. In addition the pair $-0.0746 \pm j0.4077$ is poorly damped hence leading to the requirement of implementing first stability augmentation to improve over these two undesirable characteristics. This Matlab example is designed to locate the closed-loop dynamic modes at the following locations

$$\begin{aligned} \begin{bmatrix} -24.4645 \\ -16.3686 + j3.8325 \\ -16.3686 - j3.8325 \\ -14.4513 \\ -2.7069 \\ -0.3002 \\ -0.0113 \\ -0.0131 \end{bmatrix} \end{aligned}$$

(7.39)

with the purpose to speed up the response (larger real parts), stabilise the unstable pair (closed-loop poles with negative real parts) and reduce damping (poles with no or small imaginary component relative to its real part), see Fig. 7.4. This example uses the following gain matrix when the stability augmentation system is implemented as Output Feedback

Fig. 7.4

Poles of rotorcraft dynamics and the augmented stability system.

$$\begin{aligned} F = \begin{bmatrix} 10.8486 &{}-1.7702 &{}0.0093 &{}1.1523 &{}-0.1259\\ -1.1653 &{}-0.1922 &{}0.0193 &{}-0.1281 &{}-0.0715\\ -5.7960 &{}2.1839 &{}-1.0498 &{}-0.5245 &{}0.3714 \end{bmatrix} \end{aligned}$$

(7.40)

Alternatively, if the scheme is implemented as State Feedback, the corresponding matrix H becomes

$$\begin{aligned} H = FC = \begin{bmatrix} 0 &{}0 &{}0.5906 &{}1.5030 &{}0 &{}0.0279 &{}-0.0992 &{}0.0350\\ 0 &{}0 &{}-0.0750 &{}-0.3683 &{}0 &{}-0.1330 &{}-1.5900 &{}0.0094\\ 0 &{}0 &{}0.0325 &{}0.0138 &{}0 &{}0.0588 &{}-0.0169 &{}-1.9820 \end{bmatrix} \end{aligned}$$

(7.41)

Fig. 7.5

Frequency response of rotorcraft dynamics and the augmented stability system

The frequency response of the original dynamics and the augmented system are shown in Fig. 7.5. The singular values at each frequency represent the gain variation of the stability augmentation and an additional benefit we observe is that we obtain a lower gain variation especially in the bandwidth region (frequencies less than 10 rad/s). This would facilitate the design of the autopilot system, especially in terms of decoupling the steady-state behaviour.

7.5.2 Autopilot System

In this section we compare two design approaches discussed in Sect. 7.5.2: the conventional PID control which is provided in the Matlab demo and the Robust control design. The PID Control provided in Matlab does not have derivative part ($k_D=N=0$) and the transfer functions are

$$\begin{aligned} \text {Pitch:}&\frac{2.08}{s} + 1.050 \\ \text {Roll: }&-\frac{1.35}{s} - 0.105 \\ \text {Yaw rate:}&-\frac{2.21}{s} + 0.131 \end{aligned}$$

For more information on the tuning of these parameters, refer to the Matlab demo.

Note from the Simulation diagram in Fig. 7.3 that the implementation of the PID controller is SISO, hence it is not able to compensate for any couplings in the system. For this main reason we explore the design using the Mixed-Sensitivity design approach to explore if we can get a control design which offer better performance in terms of faster responses, comparable robustness and decoupling.

To achieve decoupling to step commands, we introduce first a pre-compensator based on the dc-gain of the stability augmentation system. Denote the transfer function of the stability augmentation system as

$$\begin{aligned} \hat{G}(s) = \hat{C} (sI-(A-BF\hat{C}))^{-1}B \end{aligned}$$

(7.42)

where $\hat{C}$ is obtained by extracting the first three rows rows of the matrix C so the output signal in this case becomes $\hat{y}(t) = [\theta (t), \phi (t),r(t)]^T$. Introducing a pre-compensator $\hat{G}(j0)^{-1}$ would allow decoupling provided $\hat{G}(j0)^{-1}$ exists. In this example this inverse exists because

$$\begin{aligned} \hat{G}(j0) = \begin{bmatrix} 0.1547 &{}-0.0633 &{}-0.0017 \\ -0.0767 &{}-0.1566 &{}-0.0030 \\ -0.1318 &{}-0.8922 &{}-0.5065 \end{bmatrix} \end{aligned}$$

(7.43)

is nonsingular. Therefore we can perform mixed-sensitivity design but for the system $\hat{G}(j0)^{-1} \hat{G}(s)$ and thus achieve decoupling of step command signals. We perform mixed-sensitivity control design by shaping the sensitivity transfer function and introducing mild restrictions on the control actions. After some iterations, we choose the performance weight parameters for $w_p(s)$ as follows:

$$\begin{aligned} M= & {} 2 \end{aligned}$$

(7.44)

$$\begin{aligned} S_0^*= & {} 2\times 10^{-2}\end{aligned}$$

(7.45)

$$\begin{aligned} \upomega _S^*= & {} 1.5~\mathrm {rad/s} \end{aligned}$$

(7.46)

We choose the control input weight $w_{KS} = 0.15$ because the maximum step command amplitude $\bar{c}$ is assumed to be around 5 and we assume enough control input authority such that $\bar{u} \le 33 \approx 0.15^{-1} \times 5$ for every control input at steady-state.

Fig. 7.6

Autopilot sensitivity

Fig. 7.7

Autopilot control actions

Fig. 7.8

Autopilot co-sensitivity

Fig. 7.9

Autopilot robustness

The results are first examined in the frequency domain as shown in Figs. 7.6, 7.7, 7.8 and 7.9:

• Inspecting the sensitivities S(s) in Fig. 7.6, it is clear the PID controller performs poorly when providing disturbance rejection to step signals and low frequencies disturbances. For some combination of disturbance amplitudes and phases, the sensitivity can provide very good results but in some other directions the largest singular value is significantly high hence not securing a good disturbance rejection in all directions and actually not being acceptable in practice. On the contrary, the H-infinity controller provides an excellent sensitivity shape and we can see very small variations between the largest and lowest singular values across all frequencies, ensuring excellent disturbance rejection capabilities regardless of amplitude and phase combinations in the disturbance signals. The design upper bound is satisfied at all frequencies and the bandwidth achieved is $\upomega _S \approx 2.4$ rad/s, suggesting sufficiently fast responses and exceeding the design requirement set by $\upomega _S^*$. The sensitivity peak is just above 1 suggesting that worst-case performance does not amplify the disturbance signal significantly at the frequency where the peak occurs. Finally, the singular values of the sensitivity at low frequencies are around 0.01 (−40 dB), exceeding the initial design requirement of $S_0^*$. This very low gain at low frequencies translates in achieving integral action effectively, in other words, total attenuation to step disturbances.

• The H-infinity controller offer significantly lower control input energy when comparing the gain of KS in the low-frequency region between the two approaches, see Fig. 7.7. Large gains to particular directions can lead to extremely large control actions with the PID controller which could not meet actuator or real operation requirements. The H-infinity does not actually meet the initial upper bound requirement for a range of low frequencies so further time-domain simulations would need to be implemented to assess whether these control actions are effectively acceptable or not, and if not, further tuning would be required.

• The co-sensitivity frequency response shown in Fig. 7.8 achieved by both controllers are very good and quite similar. Both designs are excellent in the sense that there is not much difference between the lowest and largest singular values in the bandwidth region of operation, with the gains being very flat and practically 1. The H-infinity controller appears to offer a better co-sensitivity bandwidth around 2.5 rad/s, instead of 0.79 rad/s offered by the PID control scheme.

• The multivariable Nyquist stability criterion implemented in Fig. 7.9 shows that both designs are fairly robust in the sense that they are sufficiently far from the critical point

  $$\begin{aligned} | \text {det}(I + \hat{G}(j\upomega )K(j\upomega )) | \ge 0.5, \forall \upomega \end{aligned}$$

  (7.47)

  Around 9.14 rad/s, the above value for the PID controller is closer 0 than the H-infinity hence suggesting that the H-infinity offer slightly better robustness characteristics. This design would suggest that both feedback control methods offer a certain level of tolerance, preserving stable operation in the presence of changes in the rotorcraft dynamics.

Fig. 7.10

Pitch tracking and regulation

Fig. 7.11

Roll tracking and regulation

Fig. 7.12

Yaw rate tracking and regulation

Fig. 7.13

Lateral cyclic control actions

Fig. 7.14

Longitudinal cyclic control actions

Fig. 7.15

Tail rotor collective control actions

We assess now the performance in the time-domain. We show the simulations to step commands and disturbances in Figs. 7.10, 7.11, 7.12, 7.13, 7.14 and 7.15. The simulation is performed so a step pitch command with amplitude of 3.16 deg is introduced at 1 s, followed by a negative roll step command at 5 s and asking the flight control system to regulate the yaw rate at 0 deg/s throughout the simulation time. To also assess the disturbance rejection characteristics, we introduce a step disturbance on the yaw rate at 15 s with an amplitude of 5 deg/s. We observe overall that the H-infinity controller offer better performance in terms of decoupling among the rotorcraft axes and achieving faster responses (this was expected from the assessment in the frequency domain). Inspecting Fig. 7.11 we observe a noticeable roll response with the PID controller when the pitch command is introduced at 1 s, while the H-infinity is practically insensitive in this case. The pitch response shown i Fig. 7.10 appears to be largely decoupled to both the yaw rate disturbance and the roll command references in both controllers.

The worst performance we observe in the simulation is shown in Fig. 7.12. The disturbance rejection characteristics of the PID controller to step yaw rate disturbances is very poor. On the other hand, the H-infinity autopilot system offers an excellent level of disturbance rejection by keeping the yaw rate close to 0 throughout the simulation time, clearly outperforming the PID controller. As shown in Figs. 7.13, 7.14 and 7.15, cyclic and tail collective control signals performed by the H-infinity controller are much larger in magnitude than the PID controller during the transient, fitting the original control input constraints.

7.6 Concluding Remarks

We have discussed in this chapter state-of-the-art control design methods and have applied them to the flight control design problem of a conventional helicopter, demonstrating key benefits in terms of improved performance, robustness and simpler tuning procedures. We did not discuss implementation implications between classical control and robust control methods. Typically, robust control laws incur in higher implementation costs associated with larger memory requirements and additional computational burden. However, such higher costs are expected to pose no limitations in modern engineering applications given the high processing power of existing embedded systems. The presentation of the topics in this chapter around the robust control methods were constructed using a very informal mathematical terminology to facilitate the introduction of the concepts and focus on the benefits of this control strategy. For a more comprehensive and detailed treatment on Robust Control the Reader is referred to the provided references. Finally, we have shown that the control design always demands an exhaustive assessment both in the frequency domain and the time domain to have a reliable assessment. For instance, the PID autopilot provided in the Matlab demo could hint at acceptable performance if assessing only tracking characteristics and no disturbance rejections. This is misleading and the comprehensive assessment in the frequency domain highlighted the weakness in decoupling the system and poor disturbance rejection characteristics. Comprehensive assessment campaign of the flight control system is necessary to build very good confidence on the performance and robustness characteristics of the control design and also for certification purposes. In some applications, the performance and robustness benefits offered by advanced control design methods might not justify the additional implementation requirements so it is the task of the flight control design engineer to overweight these conflicting requirements and choose a strategy which achieve a desired trade off among the many conflicting requirements.