Abstract
This chapter goes into more detail about estimating divergence times from molecular sequence data. The chapter explains the inadequacy of confidence intervals for quantifying the uncertainty in divergence times. A simple method of improving the uncertainty quantification is provided. Exercises at the end of the chapter give the readers experience with quantifying the uncertainty in divergence times.
In the space of one hundred and seventy-six years the Lower Mississippi has shortened itself two hundred and forty-two miles. That is an average of a trifle over one mile and a third per year. Therefore, any calm person, who is not blind or idiotic, can see that in the Old Oolitic Silurian Period, just a million years ago next November, the Lower Mississippi River was upwards of one million three hundred thousand miles long, and stuck out over the Gulf of Mexico like a fishing-rod. And by the same token any person can see that seven hundred and forty-two years from now the Lower Mississippi will be only a mile and three-quarters long, and Cairo and New Orleans will have joined their streets together, and be plodding comfortably along under a single mayor and a mutual board of aldermen. There is something fascinating about science. One gets such wholesale returns of conjecture out of such a trifling investment of fact.
– Mark Twain1
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Divergence time
- Confidence interval
- Bootstrap proportion
- Credible interval
- Bayesian
- Fossil record
- Quantified uncertainty
- Unquantified uncertainty
- Corrected confidence level
- Correction of unquantified uncertainty
A divergence time is the amount of time that elapsed since the ancestors of present-day sequences began different paths of evolution from their common ancestor. It tells us how long ago the most recent ancestor of the sequences would have existed.
Divergence times are typically estimated using the branch lengths of an estimated phylogenetic tree like one of Chap. 3. The fossil record is often used for calibration, transforming branch lengths to divergence times. A time tree is a phylogenetic tree with divergence time estimates [53, chapter 15].
The concepts of divergence times and time trees were explained in Sect. 1.1 using an example featuring three variants of a virus. This chapter addresses the need to propagate uncertainty in the model and clade to phylogenetic trees constructed from sequence data.
4.1 Confidence Intervals of Divergence Times
Many computer programs for computing divergence times report some of the uncertainty about them in terms of confidence intervals in addition to single numbers called point estimates. A confidence interval depends on a level, usually 95%. For example, instead of reporting a divergence time as a point estimate such as \(82 \operatorname {\mathrm {{MY}}}\) (82 million years ago), we might report \(\left [28 \operatorname {\mathrm {{MY}}},230 \operatorname {\mathrm {{MY}}}\right ]\) as the 95% confidence interval [19]. The \(28 \operatorname {\mathrm {{MY}}}\) and the \(230 \operatorname {\mathrm {{MY}}}\) are called the lower limit and the upper limit of the confidence interval.
If all of the assumptions in the estimation method were correct, the 95% level is the proportion of simulated data sets for which the true divergence time would be between the limits of the confidence interval computed on the basis of each data set. That could only be interpreted as an exact probability that the true divergence time is in the interval if all of the assumptions in the estimation method were correct, which is never the case. The uncertainty about many of the assumptions can be quantified by lowering the level of the interval, as will be seen in Sect. 4.2.
For now, we will only reduce the confidence level to address the uncertainty about the clade that gives the divergence time its meaning. A level of certainty of each clade can be estimated by the bootstrap proportion (92, chapter 9; 53, chapter 6), which is available as an option in MEGA [74, 108]. The bootstrap proportion is a number between 0 and 1 that tends to be lower when there is more uncertainty about whether the clade of the estimated tree is correct. Since the bootstrap proportion estimates the probability that the clade is correct, it may be multiplied by the confidence level in order to adjust it for uncertainty about the clade [19]. For example, if the \(\left [28 \operatorname {\mathrm {{MY}}},230 \operatorname {\mathrm {{MY}}}\right ]\) confidence interval depends on a clade with a bootstrap proportion equal to 84%, then, since 0.84 × 0.95 = 0.80, we would report \(\left [28 \operatorname {\mathrm {{MY}}},230 \operatorname {\mathrm {{MY}}}\right ]\) as an 80% confidence interval rather than as a 95% confidence interval [19]. For additional examples or for guidance for using software to correct not only the level but also the interval itself, try Exercise 1. The reasoning behind the multiplication rule is explained in Sect. 4.3.
4.2 Uncertainty in Divergence Time Estimates
4.2.1 Sources of Uncertainty in Divergence Time Estimates
Uncertainty in estimates of divergence time (Sect. 4.1) calls for “healthy skepticism” regardless of how big the data set is [27, Boxes 1, 3]. Here are some of the many sources of uncertainty:
4.2.1.1 Uncertainty About Phylogenetic Trees
The general sources of uncertainty listed in Sect. 3.4 introduce uncertainty in the topologies and branch lengths needed to estimate divergence times. For example, the assumption of a common ancestor (Sect. 1.2.1) is crucial to correctly aligning the sequences. Evolutionary conclusions drawn from incorrect alignments are invalid (Sect. 3.4.1), and yet errors in automated alignments cannot be checked manually if the number of sequences is too large [27].
Even given a correct alignment, there is also considerable uncertainty in trees due to uncertainty in substitution models (Sect. 3.4.4). Methods of estimating divergence times that do not rely on the molecular clock hypothesis instead rely heavily on model assumptions [69]. Estimating divergence times from trees constructed from molecular sequences relies on model assumptions mostly made to enable calculations instead of being based on actual observations [103]. For example, uncertainty about the substitution model can lead to differences of divergence time estimates as large as hundreds of millions of years in the cases of animals and by almost a billion years in the case of cyanobacteria [27].
Uncertainty about the model is not reflected in confidence intervals since each confidence interval depends on the assumptions behind the model used to compute it [27]. Bromham et al. [28] recommend reporting the range of results from using different models. Confidence intervals from different models can then be combined by reporting a single interval with its lower limit as the minimum of the models’ lower limits and its upper limit as the maximum of the models’ upper limits (Exercise 6a). That agrees with the method of Bickel [19] whenever the confidence intervals overlap but is more cautious in other cases. Exercise 6b illustrates the less conservative method of Bickel [15].
The confidence intervals may incorporate some of the uncertainty about trees when the level of confidence is corrected using the method of Sect. 4.1. For divergence time estimation, Yang [133, §10.3.1] recommends methods that make the guesses needed to construct bifurcating trees (e.g., Fig. 3.4) rather than methods that represent uncertainty in the topology by polytomies (e.g., Fig. 3.3).
The Bayesian analog of a confidence interval is called a credible interval. Fully Bayesian models would be ideal for propagating uncertainty were their assumptions true. However those assumptions include prior distributions, which are probability distributions that are not estimated from data but rather are given as input to Bayes’s theorem (Sect. 1.2.3).Footnote 2 Uncertainty resulting from the use of prior distributions is discussed in Sect. 4.2.1.5. Narrow credible intervals do not necessarily indicate less uncertainty, for they can instead indicate conflicts between the model and the data [41]. Another indication of conflict with the data is too much agreement between the prior distributions and the posterior distributions, the data-dependent probability distributions that update the prior distributions [27]; see Sect. 4.2.1.5.
4.2.1.2 Uncertainty About Fluctuations in the Substitution Rate
Variations in the rate of evolution contribute to uncertainty about divergence times [103]. The simplest methods of estimating divergence times must assume the molecular clock hypothesis that was discussed in Sects. 1.2.2 and 3.1.2.1. More complicated methods allow the rate of substitution to change in various ways but then must rely on assumptions about how the rate might have changed over time. Since we do not know how the substitution rate has changed over time, it must be modeled mathematically, as, for example, for Fig. 1.1. Different models account for different sources of uncertainty about fluctuations in the substitution rate (Sect. 1.2.2; Yang 133, §10.3.3). For example, uncertainty about whether the scale-free models of Sect. 2.8 accurately describe molecular evolution increases the uncertainty about results from scale-dependent models.
Substitution rates can vary substantially even for very similar species, and variations in those rates cannot necessarily be accurately estimated [27]. Since, given enough sequences, the substitution rate is approximately the number of substitutions divided by the time interval between two nodes on the tree, it could in theory be estimated given a reliable estimate of the number of substitutions and a reliable estimate of the time interval based on the fossil record. When the time interval is unknown, it can be accurately estimated only given both a reliable estimate of the number of substitutions and a reliable estimate of the rate. That rate in turn could only be an estimate with some probabilistic assumptions about how the rate might differ from the rate estimated on the parts of the tree covered by the fossil record. Those assumptions underly methods based on relaxed clock models [27]. As noted in Sect. 3.4.4, more complex models do not necessarily lead to better results. Those models can be tested to some extent, but passing a test is not evidence that the model is reliable [27].
While more sequence data can reduce uncertainty in branch lengths, that does not reduce uncertainty in divergence times due to variations in rates of evolution between branches [114]. In fact, divergence times are more sensitive to changes in model assumptions and in fossil calibrations than to increasing amounts of molecular data [79]. More generally, since divergence times are not observed but rather are historical inferences, increasing the number of sequences used in the data analysis does not necessarily reduce the uncertainty [27].
Gillespie [47] emphasized that even models of molecular evolution that do not assume the clock rely on the assumption that the rate of evolution is stationary in the sense that that the statistical properties of rate fluctuations do not change in time. For example, all of the models represented in Fig. 1.1 imply stationarity. Because sequences are usually only available for present-day organisms, stationarity cannot be tested. Fortunately, stationarity need not be assumed for the entire history of a sequence, but only for the period of time studied.
Just as substitution rates vary across a phylogenetic tree, so do the rates of the birth and death of species. Many analyses overlook that, drawing conclusions about variations in speciation rates without testing the corresponding null hypothesis that the rates do not really change [27]. Conclusions about macroevolution can be misled by variations in speciation rates that were not included in the models that led to those conclusions [27].
4.2.1.3 Uncertainty About the Dates and Relations of Fossils
Since estimated dates of fossils are needed for calibration, uncertainty in those dates propagates to estimates of divergence times [133, §10.3.4.1]. While maximum likelihood estimation (Sect. 5.4) ignores this source of uncertainty, more sophisticated methods at least address it [133, §10.3.4.2]. In some cases, most of the uncertainty about divergence times comes from uncertainty about estimated dates of events in the fossil record, and there is always considerable uncertainty about those dates since they are necessarily based on assumptions about the distant past rather than on experiments that can be controlled in the laboratory [27].
Not only are the dates of events in the fossil record uncertain, but so are their positions on the tree [103]. Due to all the uncertainties involved, caution is needed when interpreting divergence time estimates from both the fossil record and sequence data [26, p. 459]; see Sect. 2.6.
4.2.1.4 Uncertainty in Statistical Error
Neglecting confidence intervals is a source of uncertainty that can lead to serious errors in divergence time estimates [40, p. 3]. For more on confidence intervals, see Sect. 4.2.2.
4.2.1.5 Uncertainty About Prior Distributions
As mentioned in Sect. 4.2.1.1, the Bayesian alternative to the confidence interval is the credible interval. Bayesian methods of estimating divergence times have the advantage of propagating multiple sources of uncertainty to the credible intervals.
That advantage, however, requires the specification of prior distributions that are themselves uncertain, and that source of uncertainty is not reflected in the credible intervals [28]. For example, changing prior distributions doubles the estimates of the divergence times of placental mammals [27]. Unavoidable biases in how sequences are sampled affect Bayesian methods to an extent depending on how their assumed prior distributions model the sampling procedure [27]. When the posterior distribution of divergence times agrees with the prior distribution, that may indicate that the sequence data do not affect the conclusions enough for the analysis to be considered reliable [27].
Uncertainty in the conclusions resulting from uncertainty about the prior distribution can be assessed by noting how changing that assumptions about the prior distribution affects the conclusions [27]. Since changing the prior distribution can lead to completely different conclusions, a non-Bayesian method may be used to assist in selecting a prior distribution and may in some settings be used as an alternative to a Bayesian method [7].
The confidence intervals from non-Bayesian methods and the credible intervals from Bayesian methods may then be combined by the method of taking the extremes of their limits (Sect. 4.2.1.1) [19] or by a less conservative method [15]. Those methods power the software of Exercises 1 and 6 (Sect. 4.4).
4.2.2 Quantified Uncertainty in Divergence Time Estimates
Recall that clades are clusters assumed to have a common ancestor in a phylogenetic tree (Step 5b of Sect. 3.1.2.1). The divergence time estimate between clades is a guess at how many years ago they might have separated from their most recent common ancestor. When multiple estimates of relevant fossil dates are available, it is possible to report a 95% confidence interval (Sect. 4.1) rather than a single number as the divergence time estimate.
Example 1
If the fossil record suggests  and
and  as two divergence time estimates that satisfy
as two divergence time estimates that satisfy  , then an approximate 95% confidence interval is
, then an approximate 95% confidence interval is


according to the assumption that they are independent and normally distributed. \(\blacktriangle \)
Confidence intervals address the uncertainty in statistical error, which is one of the sources of uncertainty listed in Sect. 4.2.1. Once a 95% confidence interval has been computed, its nominal confidence level of 95% can be corrected for other sources of uncertainty, as follows.
4.2.3 Correcting Unquantified Uncertainty in Divergence Time Estimates
Having stressed some of the sources of uncertainty mentioned above (Sect. 4.2.1), Donoghue and Smith [40, p. 3] warned “Unless all of these sources of error are taken into account, in addition to attempts to correlate fossil occurrences to the geological timescale, and those errors attendant to molecular clocks themselves, errors will propagate, potentially beyond the age of the events being estimated.” Many of those issues remain unresolved by current models, leaving unanswered questions about the evolution of animals [26, pp. 457–460] that were raised in the 1990s (Sect. 2.4), in spite of Aris-Brosou and Yang [5] and later studies.
One way to address that problem is to correct the 95% confidence level of confidence intervals (Sect. 4.2.2) using the concept of the proportion of unquantified uncertainty [cf. 13, 14]. That proportion of uncertainty not captured by the confidence interval is a percentage abbreviated by the letter  . For example, if the 95% confidence interval fails to account for half of the relevant uncertainty, then
. For example, if the 95% confidence interval fails to account for half of the relevant uncertainty, then  .
.
More precisely,  is the probability that certain results of data analysis do not apply. Said differently,
is the probability that certain results of data analysis do not apply. Said differently,  , the proportion of quantified uncertainty, is the probability that the results do apply [19]. That probability is multiplied by probabilities in the results to correct them for unquantified uncertainty. For example, we saw in Sect. 4.1 that the bootstrap proportion is multiplied by the confidence level to adjust it for some of the unquantified uncertainty about the clade.
, the proportion of quantified uncertainty, is the probability that the results do apply [19]. That probability is multiplied by probabilities in the results to correct them for unquantified uncertainty. For example, we saw in Sect. 4.1 that the bootstrap proportion is multiplied by the confidence level to adjust it for some of the unquantified uncertainty about the clade.
The corrected confidence level is reduced from 95% to


In the case of the  example, the corrected confidence level is
example, the corrected confidence level is
That means that we would be only 48% sure that the divergence time is in the calculated confidence interval. That is much less than the 95% confidence interval we would have if there were no unquantified uncertainty  .
.
4.3 Excursus: Why Multiply Probabilities by the Proportion of Quantified Certainty?
The proportion of quantified uncertainty (Sect. 4.2.3) is the probability that the model assumptions are close enough to the truth for practical purposes. Why should that probability be multiplied by the probabilities that are based on the assumptions?
Uncertain models report a result and the conditional probability that the result holds given the condition that the assumptions of the model are true or at least adequate for practical purposes. A conservative estimate of the probability of the result is the joint probability both that the result holds and that the assumptions are an adequate approximation. That joint probability is the conditional probability multiplied by the probability of adequate assumptions, according to the definition of conditional probability (see Sect. 5.1). Putting it all together, a conservative estimate of the probability of the result is the conditional probability multiplied by the proportion of quantified uncertainty.
That explains why the 95% confidence level (Sect. 4.1) and other probabilities of results (Sects. 4.2.3 and 5.5.2) are multiplied by the bootstrap proportion or by another estimate of  . Bickel [19] provides both Bayesian and non-Bayesian justifications of this method of propagating uncertainty.
. Bickel [19] provides both Bayesian and non-Bayesian justifications of this method of propagating uncertainty.
Example 2
If the only sources of uncertainty were the uncertainty of the divergence time given the topology, the uncertainty of the topology given the homology of the aligned sequences, and the uncertainty of the homology, then the corrected confidence level of the 95% confidence interval of the divergence time would be the product of the conditional probabilities of those three assumptions. Mathematically, using the “|” character to abbreviate “conditional on”:


where  . However, that is only a lower bound on
. However, that is only a lower bound on  since those are not the only sources of uncertainty. As a result, the corrected confidence level computed in that way is only an upper bound on the probability that the divergence time is in the 95% confidence interval. \( \operatorname {\mathrm {\blacktriangle }}\)
since those are not the only sources of uncertainty. As a result, the corrected confidence level computed in that way is only an upper bound on the probability that the divergence time is in the 95% confidence interval. \( \operatorname {\mathrm {\blacktriangle }}\)
For technical details on this kind of correction of unquantified uncertainty, see Sect. 7.3, which mentions a sense in which the corrected probability is a lower bound. The nature of the uncertainty-corrected probability is further clarified in Appendix A.
4.4 Exercises
-
(1)
The following questions ask about the tree estimation result that is presented in Table 4.1.
Table 4.1 Divergence time 95% confidence intervals and bootstrap proportions for a phylogenetic tree of bacterial species [19] as estimated by the 3-parameter model of Tamura [113] -
(a)
For each of the four clades, what is the uncertainty-corrected level of the confidence interval for the divergence time after adjusting for uncertainty about the clade? Hint: for clade A, the corrected level is worked out in Sect. 4.1.
-
(b)
For each of the four clades, determine the 68% uncertainty-corrected confidence interval of the divergence time by following these steps:
-
(i)
Open https://davidbickel.shinyapps.io/NormalUncertainty/ [19] in a web browser.
-
(ii)
Enter the lower and upper limits of the 95% confidence interval given in Table 4.1.
-
(iii)
Enter the bootstrap proportion given in Table 4.1 as a conservative estimate of the probability that the clade exists.
-
(iv)
Select the button corresponding to the goal of obtaining an interval that is 68% sure of containing the divergence time, and enter that probability into the corresponding box.
-
(v)
Read the result. What to do next depends on whether the result is an “Error” or an interval:
-
(A)
If an error message indicates that 68% is too high for that clade, explain why its estimated probability of existing is incompatible with having 68% certainty in its divergence time.
-
(B)
If there is no error message, then copy the resulting 68% uncertainty-corrected confidence interval of the divergence time.
-
(A)
-
(i)
-
(c)
The reference clade is the clade used in this step to set the uncertainty-corrected confidence level for other clades. Among the three clades that have 68% uncertainty-corrected confidence intervals according to what you found in Exercise 1b, which clade has the lowest of the three bootstrap proportions? Mark it as the reference clade. Follow these steps for each of those three clades, including the reference clade:
-
(i)
Reload https://davidbickel.shinyapps.io/NormalUncertainty/ [19].
-
(ii)
Enter the lower and upper limits of the 95% confidence interval given in Table 4.1.
-
(iii)
Enter the bootstrap proportion given in Table 4.1 as a conservative estimate of the probability that the current clade exists.
-
(iv)
Select the option button corresponding to the use of a reference clade.
-
(v)
Enter the bootstrap proportion given in Table 4.1 as a conservative estimate of the probability that the reference clade exists. (This will be the same value as that of Step 1(c)iii when the current clade is the reference clade.)
-
(vi)
Copy the result.
-
(i)
-
(d)
In Exercise 1c, what is an advantage of considering the clade with the lowest of the three bootstrap proportions as the reference clade? Hint: try using other clades as the reference clade.
-
(e)
What are the advantages and disadvantages of each of these ways you incorporated uncertainty about the clade?
-
(i)
Adjusting the confidence level for unquantified uncertainty (Exercise 1a)
-
(ii)
Determining the 68% uncertainty-corrected confidence interval (Exercise 1b)
-
(iii)
Using a reference clade (Exercise 1c)
-
(i)
-
(a)
-
(2)
Why should a correction for sources of uncertainty about a divergence time that are not represented in a 95% confidence interval (Sect. 4.2.1) always result in a confidence level that is lower than 95% (Sect. 5.5.2)? In other words, why should not the uncertainty correction ever make the confidence level higher than 95%?
-
(3)
These questions show two ways to use the “fungi” time tree of http://timetree.org [75] to generate a 95% confidence interval for divergence time estimation (Sect. 4.2.2):
-
(a)
Find a node on the tree that explicitly reports a confidence interval (“CI”). What is that confidence interval?
-
(b)
Find a node on the tree that instead reports minimum and maximum divergence times (“RANGE”). Interpreting those times as
 and
and 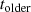 , what is the corresponding confidence interval according to Example 1 of Sect. 4.2.2?
, what is the corresponding confidence interval according to Example 1 of Sect. 4.2.2?
-
(a)
-
(4)
According to Sect. 4.2.3’s correction of the 95% level of the confidence intervals of Exercise 3:
-
(a)
What is the value of the corrected confidence level using
 ? Hint: these questions are answered for
? Hint: these questions are answered for  in Sect. 4.2.3.
in Sect. 4.2.3. -
(b)
What is the value of the corrected confidence level using
 ?
? -
(c)
What is the value of the corrected confidence level using
 ? Is that value of the corrected confidence level what you would expect if the 95% confidence interval failed to account for any of the relevant uncertainty?
? Is that value of the corrected confidence level what you would expect if the 95% confidence interval failed to account for any of the relevant uncertainty? -
(d)
What is the value of the corrected confidence level using
 ? Is that value of the corrected confidence level what you would expect if the 95% confidence interval successfully accounted for all of the relevant uncertainty?
? Is that value of the corrected confidence level what you would expect if the 95% confidence interval successfully accounted for all of the relevant uncertainty?
-
(a)
-
(5)
These foundational questions ask you to give more thought to the values of unquantified uncertainty mentioned in Exercise 4
 :
: -
(a)
In your opinion, which of those values of
 would be most appropriate for divergence times measured in numbers of months, as in viral evolution? What about for divergence times in hundreds of MYs, using the fossil record? How would you defend your answers? Hint: keep in mind the definition of the proportion of unquantified uncertainty
would be most appropriate for divergence times measured in numbers of months, as in viral evolution? What about for divergence times in hundreds of MYs, using the fossil record? How would you defend your answers? Hint: keep in mind the definition of the proportion of unquantified uncertainty  given in Sect. 4.2.3 while carefully weighing the sources of uncertainty mentioned in Sect. 4.2.1, including those listed in Sect. 3.4. Considering the bootstrap proportion of Sect. 4.1 as an upper bound on
given in Sect. 4.2.3 while carefully weighing the sources of uncertainty mentioned in Sect. 4.2.1, including those listed in Sect. 3.4. Considering the bootstrap proportion of Sect. 4.1 as an upper bound on  may also improve your reasoning about this. That upper bound may need to be multiplied by other probabilities, as seen in Example 2.
may also improve your reasoning about this. That upper bound may need to be multiplied by other probabilities, as seen in Example 2. -
(b)
What sources of uncertainty are not mentioned in Sect. 4.2.1? Hint: review the history outlined in Chap. 2 and its epigraph. How much would those additional sources increase the value of
 that you estimated in Exercise 5a?
that you estimated in Exercise 5a?
-
(a)
-
(6)
The following questions ask about the tree estimation result that is presented in Table 4.2.
Table 4.2 95% confidence intervals of the divergence times for the bacterial clades estimated as described by Bickel [19]. Whereas “Model 1” is the same model as that of Table 4.1, “Model 2” is the general time-reversible model of Nei and Kumar [92] -
(a)
Uncertainty about whether to report the confidence interval under the “Model 1” column or the “Model 2” column is an example of uncertainty about the substitution model (Sect. 3.4.4). For each of the four estimated clades, what is the smallest interval that includes all the divergence times in the intervals for both models? Hint: that is the method of uncertainty propagation explained under Sect. 4.2.1.1.
-
(b)
For each of the four clades, follow this method of determining the uncertainty-corrected credible interval:
-
(i)
Open https://davidbickel.shinyapps.io/MixtureUncertainty/ [15] in a web browser.
-
(ii)
In the box for the lower limits, enter these in order:
-
(A)
The number representing the lower limit for Model 1
-
(B)
A comma (“,”)
-
(C)
The number representing the lower limit for Model 2
-
(A)
-
(iii)
In the box for the upper limits, enter these in order:
-
(A)
The number representing the upper limit for Model 1
-
(B)
A comma (“,”)
-
(C)
The number representing the upper limit for Model 2
-
(A)
-
(iv)
Copy the resulting uncertainty-corrected credible interval.
-
(i)
-
(c)
For each of the four clades, does Exercise 6a method or Exercise 6b method give wider credible intervals? In your opinion, which method more reliably propagates uncertainty about the model? Defend your answer. Hint: Sect. 7.3 may have some ammunition.
-
(a)
References
Aris-Brosou, S., and Z. Yang. 2003. Bayesian models of episodic evolution support a late Precambrian explosive diversification of the Metazoa. Molecular Biology and Evolution 20: 1947–1954.
Battistuzzi, F.U., Q. Tao, L. Jones, K. Tamura, and S. Kumar. 2018. RelTime Relaxes the Strict Molecular Clock throughout the Phylogeny. Genome Biology and Evolution 10: 1631–1636.
Bickel, D.R. 2020. Departing from Bayesian inference toward minimaxity to the extent that the posterior distribution is unreliable. Statistics & Probability Letters 164: 108802.
Bickel, D.R. 2021a. Moderating probability distributions for unrepresented uncertainty: Application to sentiment analysis via deep learning. Communications in Statistics - Theory and Methods. https://doi.org/10.1080/03610926.2020.1863988.
Bickel, D.R. 2021b. Propagating uncertainty about molecular evolution models and prior distributions to phylogenetic trees. Working paper. https://doi.org/10.5281/zenodo.5810696.
Bickel, D.R. 2022c. Propagating clade and model uncertainty to confidence intervals of divergence times and branch lengths. Molecular Phylogenetics and Evolution 167: 107357.
Bromham, L. 2016. An Introduction to Molecular Evolution and Phylogenetics. Oxford: Oxford University Press.
Bromham, L. 2019. Six impossible things before breakfast: Assumptions, models, and belief in molecular dating. Trends in Ecology & Evolution 34: 474–486.
Bromham, L., S. Duchéne, X. Hua, A.M. Ritchie, D.A. Duchéne, and S.Y.W. Ho. 2018. Bayesian molecular dating: opening up the black box. Biological Reviews 93: 1165–1191.
Donoghue, P.C., and M.P. Smith. 2003. Telling the Evolutionary Time: Molecular Clocks and the Fossil Record. New York: CRC Press.
Dos Reis, M., and Z. Yang. 2013. The unbearable uncertainty of Bayesian divergence time estimation. Journal of Systematics and Evolution 51: 30–43.
Gillespie, J. 1994a. The Causes of Molecular Evolution. Oxford Series in Ecology and Evolution. Oxford: Oxford University Press.
Hall, B. 2018a. Phylogenetic Trees Made Easy: A How-To Manual. New York: Sinauer Associates.
Kishino, H., J.L. Thorne, and W.J. Bruno. 2001. Performance of a divergence time estimation method under a probabilistic model of rate evolution. Molecular Biology and Evolution 18: 352–361.
Kumar, S., G. Stecher, M. Li, C. Knyaz, and K. Tamura. 2018. MEGA X: Molecular evolutionary genetics analysis across computing platforms. Molecular Biology and Evolution 35: 1547.
Kumar, S., G. Stecher, M. Suleski, and S.B. Hedges. 2017. Timetree: A resource for timelines, timetrees, and divergence times. Molecular Biology and Evolution 34: 1812–1819.
Lee, M.S.Y., and S.Y.W. Ho. 2016. Molecular clocks. Current Biology 26: R399–R402.
Nei, M., and S. Kumar. 2000. Molecular Evolution and Phylogenetics. Oxford: Oxford University Press.
Ritchie, A.M., X. Hua, M. Cardillo, K.J. Yaxley, R. Dinnage, and L. Bromham. 2021. Phylogenetic diversity metrics from molecular phylogenies: modelling expected degree of error under realistic rate variation. Diversity and Distributions 27: 164–178.
Stecher, G., K. Tamura, and S. Kumar. 2020. Molecular evolutionary genetics analysis (MEGA) for macOS. Molecular Biology and Evolution 37: 1237–1239.
Tamura, K. 1992. Estimation of the number of nucleotide substitutions when there are strong transition-transversion and G+ C-content biases. Molecular Biology and Evolution 9: 678–687.
Tamura, K., Q. Tao, S. Kumar. 2018. Theoretical Foundation of the RelTime Method for Estimating Divergence Times from Variable Evolutionary Rates. Molecular Biology and Evolution 35: 1770–1782.
Twain, M. 2004. Life on the Mississippi (accessed 14 August 2021). Urbana, Illinois: Project Gutenberg. https://www.gutenberg.org/ebooks/245.
Yang, Z. 2014. Molecular Evolution: A Statistical Approach. Oxford: Oxford University Press.
Author information
Authors and Affiliations
4.1 Electronic Supplementary Materials
Supplemental 1
ancestor uncertainty (xlsx 1021 kb)
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bickel, D. (2022). Estimating Divergence Times. In: Phylogenetic Trees and Molecular Evolution. SpringerBriefs in Systems Biology. Springer, Cham. https://doi.org/10.1007/978-3-031-11958-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-11958-3_4
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-11957-6
Online ISBN: 978-3-031-11958-3
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)




 and
and 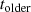 , what is the corresponding confidence interval according to Example
, what is the corresponding confidence interval according to Example  ? Hint: these questions are answered for
? Hint: these questions are answered for  in Sect.
in Sect.  ?
? ? Is that value of the corrected confidence level what you would expect if the 95% confidence interval failed to account for any of the relevant uncertainty?
? Is that value of the corrected confidence level what you would expect if the 95% confidence interval failed to account for any of the relevant uncertainty? ? Is that value of the corrected confidence level what you would expect if the 95% confidence interval successfully accounted for all of the relevant uncertainty?
? Is that value of the corrected confidence level what you would expect if the 95% confidence interval successfully accounted for all of the relevant uncertainty? :
:  would be most appropriate for divergence times measured in numbers of months, as in viral evolution? What about for divergence times in hundreds of MYs, using the fossil record? How would you defend your answers? Hint: keep in mind the definition of the proportion of unquantified uncertainty
would be most appropriate for divergence times measured in numbers of months, as in viral evolution? What about for divergence times in hundreds of MYs, using the fossil record? How would you defend your answers? Hint: keep in mind the definition of the proportion of unquantified uncertainty  given in Sect.
given in Sect.  may also improve your reasoning about this. That upper bound may need to be multiplied by other probabilities, as seen in Example
may also improve your reasoning about this. That upper bound may need to be multiplied by other probabilities, as seen in Example  that you estimated in Exercise 5a?
that you estimated in Exercise 5a?