Keywords

1 Introduction

Evaluating the seismic stability of slopes is an important task of geotechnical engineers. The performance-based permanent displacement analysis has attracted increasing attention in assessing the seismic safety of slopes, as usually conducted by the Newmark-type sliding block procedures [1,2,3]. Such procedures that approximately estimate the earthquake-induced permanent slope displacement (D) are particularly useful for preliminary screening-level analyses and regional landslide hazard mapping. For assessing the seismic performance of important slopes such as those involved in critical projects, the numerical stress-deformation analysis is necessary to provide a more accurate estimate of the slope performance [4].

The probabilistic displacement hazard approach has been well developed to estimate the hazard-consistent D [5,6,7]. Recently, this approach has been improved with the numerical slope displacement analysis [8]. As a key component, the relationship between one or multiple ground motion (GM) intensity measure (IMs) and D should be explicitly described by a regression model, in which the IMs better correlated to D (i.e., higher efficiency) are recommended as predictor variables. Therefore, it is of interest to investigate the efficiency of different IMs. However, most of the existing studies were based on the Newmark-type procedures (e.g., [9]), so the findings and conclusions may not hold for the numerical cases [8, 10]. Also, the efficiency rankings of various IMs may be dependent on slope materials, slope geometry, etc. Hence, more research efforts should be devoted to this topic.

This study aims to: (1) investigate the performance of IMs in developing D models for a cohesive-frictional slope based on numerical analysis; and (2) compare the means and standard deviations of D for these models considering uncertainties in predicting both the IMs and D via Monte Carlo simulation (MCS). The remaining part of this paper starts with a description of the procedure employed, followed by the slope model development and comparative results.

2 Procedure for Seismic Slope Displacement Analysis

The seismic slope displacement analysis procedure includes the following steps.

  1. (i)

    Select GM acceleration-time series, and compute their IMs of interest. The GMs selected should cover a wide range of the earthquake magnitude (M), rupture distance (R), and shaking intensity, etc.

  2. (ii)

    Perform dynamic analysis for the slope model using each of the GMs to obtain D.

  3. (iii)

    Develop D models based on the obtained data of D. The trend of lnD versus lnIM (i.e., in natural logarithmic scale) is fitted via one of the following formulas:

    $$ \ln D = \mu_{\ln D} + \varepsilon_{\ln D} \cdot \sigma_{\ln D} = a_1 \ln IM_1 + a_0 + \varepsilon_{\ln D} \cdot \sigma_{\ln D} $$
    (1)
    $$ \ln D = \mu_{\ln D} + \varepsilon_{\ln D} \cdot \sigma_{\ln D} = a_1 \ln IM_1 + a_2 \ln IM_2 + a_0 + \varepsilon_{\ln D} \cdot \sigma_{\ln D} $$
    (2)

    where D is in units of cm; a0, a1, and a2 are regression coefficients; εlnIM denotes a standard normal variable; σlnD is the model-specific standard deviation, so lnD follows the normal distribution with mean of μlnD and standard deviation of σlnD.

  4. (iv)

    Perform MCS to generate NIM samples of the correlated IMs. The probability distribution of lnIM is described by the associated ground motion model (GMM) with the following general expression [11]:

    $$ \ln \left( {IM} \right) = \mu_{\ln IM} \left( {M,R,{\text{etc}}{.}} \right) + \varepsilon_{\ln IM} \cdot \sigma_{\ln IM} $$
    (3)

    where \(\mu_{\ln IM} \left( {M,R,{\text{etc}}{.}} \right)\) represents the mean of lnIM estimated by using M, R, etc.; σlnIM denotes the standard deviation of lnIM given by GMM; εlnIM is a standard normal variable. Based on the joint normal distribution of lnIMs, the NIM samples can be readily generated by specifying the correlation coefficients among IMs (e.g., [12]).

  5. (v)

    Substitute each sample of IM (or IMs) into Eq. (1) (or Eq. (2)) to derive μlnD, and then perform MCS to generate ND samples of D based on the distribution of lnD. This process is repeated for NIM times, resulting in NIM × ND data points of D.

3 Slope Model Establishment

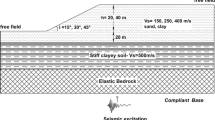
Figure 1 shows the slope model established in the finite difference code FLAC [13], where the slope height (H) and slope angle are 20 m and 30°, respectively. The cyclic soil behavior is described by the hysteretic damping model Sig4, in which the model parameters are calibrated according to the Darendeli [14] modulus reduction and damping ratio curves with plasticity index of 0 and the effective vertical stress at the depth of H. Sig4 is combined with the Mohr-Coulomb plasticity criterion for modelling the plastic behavior of soils. To remove high-frequency noises, a small amount of stiffness-proportional Rayleigh damping (0.2%) is specified. The bedrock layer is considered linear-elastic with 0.5% mass- and stiffness-proportional Rayleigh damping. Table 1 summarizes the parameters assigned to the slope model. To minimize wave reflection effects, the quiet boundary is applied along the bedrock base, and the free-field boundary that simulates a quiet boundary is implemented at both lateral sides [13]. The sum of L1 and L2 is equal to 12H, as illustrated in Fig. 1.

Fig. 1.
figure 1

Numerical model of slope and the associated maximum shear strain increment contours obtained from pseudostatic strength reduction technique. The CSS from Bishop’s simplified method is shown using a red line.

Full size image
Table 1. Summary of the geotechnical parameters assigned to the slope model.
Full size table

Before conducting dynamic analysis, pseudostatic slope stability analysis is conducted using both the strength reduction technique (SRT) and Bishop’s simplified limit equilibrium method. As also shown in Fig. 1, the resulting shear band from SRT agrees well with the critical slip surface (CSS) from the Bishop method. The fundamental period of the failure mass (above CSS) is estimated as Ts,mass = 4h/Vs = 0.077 s, where Vs is the soil shear-wave velocity (i.e., \(V_s = \sqrt {{{G_{\max } } / \rho }}\)), and h denotes the maximum thickness of the failure mass. The fundamental period of the soil layer (Ts,layer) is similarly calculated using h = 1.5H (average of the downhill and uphill soil layer thicknesses). In the next section, two degraded periods determined as Td1 = 1.5Ts,mass = 0.116 s and Td2 = 1.5Ts,layer = 0.45 s will be considered to construct the spectral acceleration (SA) for predicting earthquake-induced slope displacements (e.g., [2]).

4 Development of Slope-Specific Displacement Models

4.1 Construction of Displacement Models

The NGA-West2 database (https://ngawest2.berkeley.edu/) is used to select 83 GM records, which cover a wide range of peak ground acceleration (PGA) from 0.05 g to 1.41 g, allowing for a proper consideration of the GM record-to-record variability. Following Step (ii) in Sect. 2, the D for each GM is calculated as the maximum horizontal displacement along the slope surface.

Fig. 2.
figure 2

Distribution of D versus different IMs. Also shown are trends fitted by Eq. (1) or (2).

Full size image

For a thorough comparison, this study incorporates 10 representative IMs, including PGA, peak ground velocity (PGV), Arias intensity (IA), cumulative absolute velocity (CAV), SA(Td1), SA(Td2), acceleration spectrum intensity (ASI), spectrum intensity (SI), mean period (Tm), and significant duration Ds5–75. Among them, SA(Td1) and SA(Td2) represent the 5%-damped spectral accelerations at the periods Td1 and Td2, respectively. Note that most of the existing Newmark-type models correlate SA(Td1) to D. Step (iii) is conducted for the 10 scalar IMs and 38 combinations of IMs, resulting in 48 D models.

Figure 2 shows the D versus IM distributions for 9 scalar IMs and the fitted linear trends (and the associated σlnD). It is found that the lnD versus lnIM relationship generally follows a linear pattern. The SA(Td2) model fits the data better than the others; yet, the more usually used SA(Td1) leads to much larger scatter (i.e., σlnD is almost double). Also, the scatter for Tm and Ds5–75 is significantly larger, indicating the low efficiency of the two scalar IMs in predicting D. Such wide ranges of D and IMs imply the capabilities of the models for estimating D in various shaking levels.

4.2 Standard Deviations of the Displacement Models

Figure 3a and b further compare σlnD for the scalar-IM and vector-IM models, respectively. The order of SA(Td2) > IA > PGV > SI > CAV > ASI > PGA > SA(Td1) > Tm > Ds5–75 is observed for the efficiency of scalar IMs. The smallest σlnD of 0.76 for SA(Td2) may be attributed to that Td2 = 0.45 s (for the soil layer’s fundamental period) is comparable to the value of Tm (e.g., see Fig. 2) and is more related to the dynamic response of the slope. This indicates that the degraded period for the failure mass (i.e., Td1) should be used cautiously with the consideration of GMs’ period range. Besides, IA and PGV, which were identified as the two most efficient IMs by Cho and Rathje [8], yield similar σlnD (0.78 and 0.82) to that of SA(Td2). Hence, the three IMs may be preferred for deriving D models. Although it is not a common IM, SI also results in relatively small σlnD (≈0.8). On the other hand, Tm and Ds5–75 lead to significantly large σlnD (≈2).

Fig. 3.
figure 3

Model-specific standard deviations for different (a) scalar-IM and (b) vector-IM models.

Full size image

It is observed from Fig. 3b that the vector-IM models yield much smaller σlnD than the scalar-IM models as a result of more complementary information carried by two IMs. The order of [IA,SI] > [IA,Tm] > [SA(Td2),CAV] > [IA,PGV] > [CAV,SI] is observed for the five most efficient vectors (i.e., σlnD = 0.54–0.61). Specifically, the σlnD values (0.54 and 0.55) for [IA,SI] and [IA,Tm] are noticeably smaller, indicating the attractiveness of the two vectors. The [SA(Td2),CAV], [IA,PGV], [CAV,SI], [PGA,SI], [IA,SA(Td2)] and [PGV,CAV] are the subsequently efficient vectors that achieve comparative σlnD within the range of 0.60–0.61. These vectors include either IA or CAV, which capture multiple characteristics (amplitude, duration, etc.) of GMs.

5 Scenario-Based Comparison of the Models Using MCS

Following Step (iv), the mean and variability of the D prediction for different models are compared under some representative scenarios. Multiple GMMs are adopted for individual IMs [11, 15,16,17,18] following the logic tree method. The correlation coefficient matrix for modeling the joint distribution of the 10 IMs is derived according to the references [12, 19, 20]. Both NIM and ND are specified as 200, yielding 40000 displacement values. The geometric mean of these values (termed as Dmean hereafter) and the standard deviation of lnD (St.d. of predicted lnD) are investigated as follows.

Fig. 4.
figure 4

Mean prediction trends associated with different displacement models for VS30 = 760 m/s

Full size image

5.1 Mean of the Displacement Prediction

Figure 4 shows the Dmean versus R for VS30 = 760 m/s. Both M = 5.5 and 7.5, and the scalar- and vector-IM models are included. Note that the legend is shown in the way of illustrating the ranking of σlnD for different displacement models. The results for VS30 = 360 m/s are not shown due to the limited space, yet are also discussed as follows. First, Dmean decreases with increasing R, while the decreasing trend becomes slower for larger R. Second, the trends for the scalar- and vector-IM models are generally comparable, and the difference of the results for most vector-IM models (especially for the 10 most efficient ones) is smaller in comparison with the scalar-IM models. Third, the model-to-model difference is slightly dependent on VS30 and M. Regarding the soil site condition (VS30 = 360 m/s), M = 5.5 generally corresponds to smaller difference of Dmean than M = 7.5; yet, this observation appears to reverse for the rock site condition. Fourth, the SA(Td1) model generally produces the upper and lower bounds among the scalar-IM models for M = 5.5 and 7.5, respectively. The Tm and Ds5–75 models are two exceptional cases with almost unchanged Dmean, indicating that the two IMs should not be used solely to predict D.

5.2 Variability in the Displacement Prediction

Figure 5 displays the St.d. of predicted ln D versus R for VS30 = 760 m/s. The VS30 = 360 m/s case produces slightly smaller St.d., and is not shown here for brevity. No evident trend of St.d. versus R is observed. The St.d. values for the scalar-IM models are generally comparable to those for the vector-IM models, although the 10 most efficient vector-IM models tend to result in smaller St.d. values. As a superposition of σlnIM and σlnD, St.d. is generally within the range from 1.4 to 1.8.

Fig. 5.
figure 5

Variability trends associated with different displacement models for VS30 = 760 m/s.

Full size image

For comparison, Table 2 lists the different types of standard deviations for the scalar-IM models, where μStd represents the average of St.d. for different scenarios (various VS30 and R). It is seen that the IM for the smallest μStd may not produce the smallest σlnD, due to the additionally included uncertainty in the IM prediction. In general, CAV tends to yield smaller μStd, and μStd for IA is still relatively small. The μStd values for the 38 vector-IM models are derived and are shown in Fig. 6. A similar observation of different rankings of μStd and σlnD can be made. Specifically, the low uncertainty in estimation of CAV is illustrated again; that is, some IM vectors including CAV yield relatively small total variability (μStd). The larger μStd is, the more uncertain the displacement prediction. Though σlnD can generally be smaller than 0.75, the total uncertainty is still large, and in most cases μStd has exceeded 1.4. Take the predicted D of 40 cm given an earthquake scenario as an example; the expected range of D considering the total uncertainty (μStd = 1.4) can be estimated as [exp(ln(40)-μStd), exp(ln(40) + μStd)] = [10 cm, 162 cm] [2]. Such a large interval should be shrunk for a more robust estimation of D. Thus, more powerful GMMs with smaller aleatory variability should be developed and applied to the seismic slope displacement analysis.

Table 2. Standard deviation parameters for the scalar-IM models.
Full size table
Fig. 6.
figure 6

Comparison of μStd for different vector-IM displacement models.

Full size image

6 Summary and Conclusions

This study investigated the relationship between ground motion intensity measures (IMs) and earthquake-induced permanent slope displacement (D) based on numerical stress-deformation analyses. Ten scalar IMs and 38 vector-IM combinations, were used to develop the D models, and the efficiencies of various scalar and vector-IMs were compared in terms of the model standard deviation (σlnD). Furthermore, a Monte Carlo simulation-based procedure was utilized to compare these D models under representative earthquake scenarios, in which the uncertainties in predicting both IMs and D are considered. The comparative results lead to the following conclusions:

  1. 1.

    The SA(Td2 = 1.5Ts,layer)- and IA-based displacement models were identified as the most efficient scalar-IM models with the smallest σlnD of 0.77, while the more commonly used SA(Td1 = 1.5Ts,mass) resulted in much larger σlnD. In constrast, the scalar IMs of Tm and Ds5–75 exhibit the lowest efficiency in regressing D.

  2. 2.

    The [IA,SI] and [IA,Tm] resulted in the smallest σlnD of about 0.55 for the vector-IM models. The subsequent six most efficient models generally included ether IA or CAV. Only 6 among the 38 models yielded σlnD greater than 0.77, indicating the advantage of vector-IM models for improving the efficiency of regressing D.

  3. 3.

    The total standard deviation contributed by both the uncertainties in IM and D predictions is considerably larger than σlnD, and the models with the smallest σlnD do not necessarily yield the smallest total standard deviation. This is more evident for models including CAV in which a smaller variability is involved in predicting this IM. Recent studies on developing non-ergodic ground motion models shed light in the direction of reducing variability in the IM prediction (e.g., [21]).

The results of the mean and standard deviation of D obtained in this study could be useful to select IMs in developing predictive models for seismically-induced slope displacements. Such models can be implemented within the fully-probabilistic framework [7, 8], allowing practitioners to estimate the hazard-compatible D for seismic design of slopes.