Keywords

1 Introduction

The wireless voice and data traffic has followed exponential growth rate since many decades, which is as per the Cooper’s law (Cooper 2010, p. 2). The Ericsson mobility report (Ericsson 2021, p. 2) even forecasts growth rate more than 49% annually, which is more faster than Cooper’s law. So the Massive MIMO is one of the key enabler technology for this future demands. It is the breakthrough technology in wireless mobile communication, having large number of antennas (i.e. at least ten times of serving UEs) at Base Station (BS) as per (Björnson et al. 2017, p. 6; Ding and Jing 2019, p. 1; Björnson et al. 2016, p. 1; Larsson et al. 2014, p. 186) and this concept of Massive MIMO was firstly introduced by Thomas Marzetta in his seminal paper (Marzetta 2010). The massive number of antennas at BS allows spectral efficiency to be enhanced by beam forming and spatial multiplexing types of key techniques as per (Larsson et al. 2014, p. 187; Özdogan et al. 2019, p. 1). The tens of User Equipments (UEs) can be simultaneously served in same coherent time and frequency slot with efficient usage of hundreds of BS antennas. In Time Division Duplex (TTD) mode, Channel State Information (CSI) is estimated in up-link (UL) and assumed same for down-link (DL) as channel is assumed reciprocal in TDD protocol. As result, TDD protocol reduces estimation efforts and time, up to a large extends as per (Björnson et al. 2017, p. 209). The CSI is very important for coherent signal processing and it is obtained by piloting method. The pilot signal is know at both side and it is sent through channel to get channel response. The available channel response of pilot signal is used for CSI acquisition by comparing it with known original pilot available as per (Björnson et al. 2017, pp. 208–209).

2 Literature Review

(Yu et al. 2020, p. 1; Du et al. 2019, p. 1) investigated the SE of system with imperfect CSI for correlated Rayleigh fading models. (Demir and Björnson 2020, p. 2) derived SE for Maasive MIMO in uncorrelated Rician fading scenario. (Chen et al. 2020 p. 1; Cho et al. 2020, p. 1) has analyzed the SE performance for LoS type of channel only, called no fading. Usually in real scenario, channel has direct (LoS) and indirect (NLoS) propagation paths, where the large scale fading results from Line of Sight (LoS) and the small scale fading results from Non-Line of Sight (NLoS) types of propagations as per (Tse and Viswanath 2005, p. 21). As per (Boukhedimi et al. 2020, p. 1; Femenias et al. 2020, p. 1; Jin et al. 2021, p. 1; Liu et al. 2021, p. 1; Peng et al. 2021, p. 1; Boukhedimi et al. 2019, p. 1) the Rician channel fading model can closely represent the real channel fading scenario than Rayleigh one.

This Rician channel model has not much analyzed compared to Rayleigh for Massive MIMO SE as per (Wang et al. 2020, p. 2; Boukhedimi et al. 2019, p. 1). (Boukhedimi et al. 2019, p. 1; Rajmane and Sudha 2019, p. 1) have considered single cell system for SE analysis. Also (Boukhedimi et al. 2019, p. 6) have considered multi-cell scenario but assumed that the LoS can exist only within the cell area and not in between UE and BS belonging from different cells. In large, the Rician channel fading model is limited up to cell boundaries and inter cell channel fading is of Rayleigh fading type only. (Ding and Jing 2019, p. 1; Liu et al. 2020, p. 2) have carried out SE analysis for Massive MIMO system using zero-forcing precoding method. However (Jin et al. 2021, p. 1; Kong et al. 2019, p. 1; Peng et al. 2021, p. 1; Wang et al. 2020, p. 1; Wang et al. 2021, p. 1) has derived SE for Massive MIMO using maximum ration precoding method. As per (HOSANY 2020, pp. 35–36; Rajmane and Sudha 2019, p. 1) maximum ration precoding is simpler than zero forcing precoding in the context of computational complexity. (Liu et al. 2021, p. 1; Özdogan et al. 2019, p. 1; Wang et al. 2021, p. 1; Demir and Björnson 2020, p. 1; Özdogan et al. 2019, p. 1) have derived SE for Massive MIMO using various estimation methods and MMSE estimation found best among all (Arzykulov et al. 2021, p. 2; Boukhedimi et al. 2019, p. 1; Ding and Jing 2019, p. 1; Kong et al. 2019, p. 2; Peng et al. 2021, p. 1; Yu et al. 2020. P. 2; Du et al. 2019, p. 1) all this works assumed imperfect CSI for SE derivation in Massive MIMO, which is the case in real scenario. On the contrary previous works (HOSANY 2020, p. 1; Rajmane and Sudha 2019, p.1; Björnson et al. 2016. P. 119) have assumed perfect CSI for SE analysis in Massive MIMO. Both perfect CSI and imperfect CSI scenarios are considered in (Liu et al. 2020, p. 2) for SE derivation in Massive MIMO.

3 Core Contribution

There are limitations of previous works and it is extended here as follows. (1) Mostly in previous works, fading scenarios are considered uncorrelated, which is not in practice as scattering clusters are finite as per (Björnson et al. 2017, p. 237). and it is broaden by considering correlated scenarios also here to compare it with uncorrelated scenario. (2) Mostly in previous works, fading scenario across the cells are assumed Rayleigh, which is not the reality, because there can be LoS between cell edge UE of cell A to BS of cell B i.e. large areas without obstructions, densification of small cells in given area, and unmanned vehicles serving from air (UAVs). (3) Mostly in previous works, single cell scenario is considered, which is again far away from reality and it is extended by considering multi-cell scenario here. (4) In futuristic mmWave technology, path loss can increase more. As consequence to compensate with that loss, cell area and cell densification in given area can be increased, this increases probability to have LoS more. So LoS existence cannot be avoided absolutely. So the 3GGP model (3GPP Tech. Report 2020, 26) is used in our simulation, where fading is considered as Rician (LoS + NLoS) and compared with Rayleigh (NLoS). To implement above extensive approach, below have been considered:

  • In multi-cell system, UE and BS can have Rician or Rayleigh correlated fading channel.

  • To acquire CSI, MMSE, EW-MMSE and LS estimation methods are used and MR precoding technique is used for transmit precoding from BS.

    And below has been carried out:

  • Average sum DL SE has been analyzed for above mentioned estimation methods and fading scenarios.

  • Average sum DL SE has also been analyzed for correlated and uncorrelated fading scenarios.

  • Cumulative density function (CDF) of SE per US has also been analyzed for same above estimation methods and fading scenarios.

4 Channel and System Modeling

It is considered that the each BS is equipped with hundreds of antennas in the system. Also the total coverage area is divided in to the L cells and each cell has the dedicated BS equipped with Mj number of antennas. In each cell the K numbers of UEs are served by same BS. The channel between BS and UE is operated in TDD mode, where channel response found constant over coherent slot sized of \({\tau }_{c}\) samples and channel realization assumed independent over any pair of coherent slots. The coherent slot size \({\tau }_{c}\) depends on mobility of UE and surrounding environment as per (Björnson et al. 2017, p. 263). The \({\tau }_{c}\) samples can be divided into \({\tau }_{P}\),\({\tau }_{u},\mathrm{and} {\tau }_{d}\) samples as per their role, like \({\tau }_{p}\) samples for UL pilot signaling, \({\tau }_{u}\) samples for UL data transmission, and \({\tau }_{d}\) samples for DL data transmission. As per TTD protocol, the channel is assumed reciprocal. As result, the channel is estimated in UL and assumed same in DL, which reduces channel estimation time, resources and efforts compared to FDD protocol. However, before data transmission, channel is estimated by piloting method.

The channel response of propagation is denoted as \({h}_{lk}^{j}\in {\mathbb{C}}^{{M}_{j}}\), where l indicates cell number, k indicates UE number and j indicates BS number. These notations are same throughout the paper. The \({h}_{lk}^{j}\in {\mathbb{C}}^{{M}_{j}}\) is vector and each element of it represents individual channel response between UE and individual BS antenna. For notational convenience, \({h}_{lk}^{j}\) is the UL channel and as per TDD protocol DL channel is \({{(h}_{lk}^{j})}^{H}\), in same coherent slot.

The \({h}_{lk}^{j}\in {\mathbb{C}}^{{M}_{j}}\) channel considered spatially correlated Rician fading and it is expressed as

$${h}_{lk}^{j} \sim {\mathcal{N}}_{\mathbb{C}} \left({\overline{h} }_{lk}^{j}, {R}_{lk}^{j}\right),$$
(1)

where \(\forall j, l \in 1,\dots .,L\) and \(\forall k \in 1,\dots .K\) and \({\mathcal{N}}_{\mathbb{C}}\) indicates that the channel realizations are assumed as circularly symmetric complex Gaussian distributed. The \({\overline{h} }_{lk}^{j} \in {\mathbb{C}}^{{M}_{j}}\) signify LoS component of channel and \({R}_{lk}^{j} \in {\mathbb{C}}^{{M}_{j}\times {M}_{j}}\) signify NLoS component of channel in Eq. (1), where \({R}_{lk}^{j} \in {\mathbb{C}}^{{M}_{j}\times {M}_{j}}\) is positive semi-definite covariance matrix. The Gaussian distribution represents the small-scale fading and large-scale fading can be represented by shadow fading, path loss, radiation patterns of antennas. The large scale fading is represented by \({R}_{lk}^{j}\) and \({\overline{h} }_{lk}^{j}\). The trace of \({R}_{lk}^{j}\) normalized over \({M}_{j}\) indicates average channel gain, as shown in Eq. (2). It is also called large-scale channel gain or fading co-efficient.

$${\beta }_{lk}^{j}= \frac{1}{{M}_{j}} tr\left({R}_{lk}^{j}\right),$$
(2)

5 Estimation Methods

The CSI is very essential for signal processing at receiver and transmitter, which can be acquired by piloting method, where \({\tau }_{P}\) samples are transmitted as pilot signals in same coherent slot. There is set of pilot sequences, known at UE and BS both and transmitted from UE to BS in UL. In multi-cell scenario, this same set can be reused in more than one cell by UEs and each individual sequence is unique within the cell for each UE. The pilot sequence is denoted as \({\varnothing }_{jk}\in {\mathbb{C}}^{{\tau }_{P}}\), where \({\Vert {\varnothing }_{jk}\Vert }^{2}= {\tau }_{P}\). The pilot sequence set is expressed as,

(3)

where k and i are UE numbers and l and j are cell numbers. The \({Y}_{p}^{j}\upepsilon {\mathbb{C}}^{{M}_{j}\times {\tau }_{P}}\) is the pilot signal received at BS j, expressed as,

$${Y}_{p}^{j}=\sum\nolimits_{k=1}^{{K}_{j}}\sqrt{{P}_{jk}}{h}_{jk}^{j}{\varnothing }_{jk}^{T}+ \sum\nolimits_{\begin{array}{c}l=1\\ l \ne j\end{array}}^{L}\sum\nolimits_{i=1}^{{K}_{l}}\sqrt{{P}_{li}}{h}_{li}^{j}{\varnothing }_{li}^{T}+ {N}_{j}^{p},$$
(4)

where \({N}_{j}^{p}{\epsilon {\mathbb{C}}}^{{M}_{j}\times {\tau }_{P}}\) and \({N}_{j}^{p}\sim \mathcal{N}_{\mathbb{C}}\left(0, {\sigma }_{ul}^{2}\right)\). The known UE’s pilot sequence \({\varnothing }_{li}^{*}\) is multiplied with received \({Y}_{p}^{j}\) signal at BS j to obtain \({y}_{jli}^{p}\) as shown in Eq. (5) below,

(5)

where \({y}_{jli}^{p}\in {\mathbb{C}}^{{M}_{j}}\) is the enough statistic for estimating \({h}_{li}^{j}\) as per (Özdogan et al. 2019, p. 2).

However the statistical channel knowledge required by channel estimator is differ from estimator to estimator and three channel estimators are considered here namely MMSE, EW-MMSE and LS. The statistical distribution of estimated channel can be obtained from the sample mean and sample covariance matrices (Özdogan et al. 2019, p. 2; Kay 1993).

5.1 MMSE Channel Estimator

The channel estimation \({\widehat{h}}_{li}^{j}\) as shown below in Eq. (6), can be acquired at BS by applying MMSE estimation method to process received pilot signal shown in Eq. (5),

$${\widehat{h}}_{li}^{j} = {\overline{h} }_{li}^{j}+ \sqrt{{P}_{li}}{R}_{li}^{j}{\Psi }_{li}^{j} ({y}_{jli}^{p}- {\overline{y} }_{jli}^{p})$$
(6)
(7)

The perfect channel estimation is ideal case and usually not possible to achieve in practice. There is always some non zero channel estimation error generated, which is defined as \({\tilde{h }}_{li}^{j}= {h}_{li}^{j}- {\widehat{h}}_{li}^{j}\) and the covariance matrix of estimation error is expressed as

$${C}_{li}^{j}= {R}_{li}^{j}-{P}_{li}{\tau }_{P}{R}_{li}^{j}{\Psi }_{li}^{j}{R}_{li}^{j}$$
(8)

where the trace of \({C}_{li}^{j}\) matrix is the mean square error, also defined as \({\mathbb{E}}\left\{{\Vert {h}_{li}^{j}- {\widehat{h}}_{li}^{j}\Vert }^{2}\right\}.\) The distribution of channel estimation and estimation error can be expressed as below,

$${\widehat{h}}_{li}^{j} \sim {\mathcal{N}}_{\mathbb{C}} \left({\overline{h} }_{li}^{j}, {R}_{li}^{j}-{C}_{li}^{j}\right)$$
(9)
$${\tilde{h }}_{li}^{j}\sim {\mathcal{N}}_{\mathbb{C}} \left({0}_{M}, {C}_{li}^{j}\right)$$
(10)

where \({\widehat{h}}_{li}^{j}\) and \({\tilde{h }}_{li}^{j}\) are independent random variables. It can be noticeable from Eq. (8) and (10) that, the channel estimation error and covariance matrix are not depending on channel mean. Also means of channel vector are deterministic and can be filtered out by receive signal processing and the estimation error does not affected by channel vector means. It is assumed independent channel realization, but it is not necessary that channel estimates are also independent. It can be understood as follows. There are UEA in cell A and UEB in cell B using same pilot sequence to estimate the channel. Now, if channel estimation of UEA is of our interest, then due to having same pilot sequence, channel estimation at BS in cell A between UEA and BS in cell A is contaminated by unnecessary pilot sequence received by BS in cell A from UEB in cell B, called pilot contamination. In general it can be said that, it occurs due to the same pilot sequence used by more than one UEs in different cells to reduce pilot over head. The \({\widehat{h}}_{jk}^{j}\) is channel estimation of channel between user equipment k and BS j in cell j, where (j, k) \(\in\) . However it is expressed as below,

$${\widehat{h}}_{jk}^{j}= {\overline{h} }_{jk}^{j}+ \sqrt{{P}_{jk}}{R}_{li}^{j}{\Psi }_{li}^{j} ({y}_{jli}^{p}- {\overline{y} }_{jli}^{p})$$
(11)

The \({\widehat{h}}_{jk}^{j}\) is correlated with \({\widehat{h}}_{lk}^{j}\) since \({y}_{jli}^{p}\) common in both expressions and \({\Psi }_{li}^{j}= {\Psi }_{jk}^{j}\).

5.2 Element-Wise MMSE Channel Estimator

There can be a case, where full covariance matrices are not available at BS. In such case, MMSE estimation is not as effective as it can be due to lake of statistical information and EW-MMSE estimation is suitable option in such cases (Özdogan et al. 2019, p. 3; Björnson et al. 2017, p. 266). However, EW-MMSE estimates only diagonal elements of matrices and off-diagonal element do not estimated by EW-MMSE, where off-diagonal elements represents correlations between elements. So, EW-MMSE does not required inverse matrix operation, which reduces computational efforts substantially. The EW-MMSE channel estimation is expressed as,

$${\widehat{h}}_{li}^{j}= {\overline{h} }_{li}^{j}+\sqrt{{P}_{li}}{D}_{li}^{j}{\Lambda }_{li}^{j} ({y}_{jli}^{p}- {\overline{y} }_{jli}^{p})$$
(12)

\({\rm{where}}\,{{D}_{li}^{j}\upepsilon {\mathbb{C}}^{{M}_{j}\times {M}_{j}}\,\rm{and}}\,{\Lambda }_{li}^{j}\upepsilon {\mathbb{C}}^{{M}_{j}\times {M}_{j}}\) are diagonal matrices with \(D_{{li}}^{j} = diag \Big(\Big[{R}_{li}^{j}\Big]_{mm}:m=1\dots {M}_{j}\Big)\) and \({\Lambda }_{li}^{j}=diag\Big(\Big[\sum_{{ {(l}^{^{\prime}}, {i}^{^{\prime}})\in p}_{li}}{P}_{{l}^{^{\prime}}{i}^{^{\prime}}}{\tau }_{P}{R}_{{l}^{^{\prime}}{i}^{^{\prime}}}^{j}+{\sigma }^{2}{I}_{{M}_{j}}\Big]_{mm}: m=1\dots {M}_{j}\Big)^{-1}\). The \({\widehat{h}}_{li}^{j}\) and \({\tilde{h }}_{li}^{j}\) are distributed as,

$${\widehat{h}}_{li}^{j} \sim {\mathcal{N}}_{\mathbb{C}} \left({\overline{h} }_{li}^{j}, {\Sigma }_{li}^{j}\right)$$
(13)
$${\tilde{h }}_{li}^{j} \sim {\mathcal{N}}_{\mathbb{C}} \left({0}_{M}, {\stackrel{\sim }{\Sigma }}_{li}^{j}\right)$$
(14)

where \({\tilde{h }}_{li}^{j}\) is channel estimation error, \({\Sigma }_{li}^{j}= {P}_{li}{\tau }_{p}{D}_{li}^{j}{\Lambda }_{li}^{j}{({\Psi }_{li}^{j})}^{-1}{\Lambda }_{li}^{j}{D}_{li}^{j}\) and\({\stackrel{\sim }{\Sigma }}_{li}^{j}= {P}_{li}{\tau }_{p}{R}_{li}^{j}{\Lambda }_{li}^{j}{D}_{li}^{j}-{P}_{li}{\tau }_{p}{D}_{li}^{j}{\Lambda }_{li}^{j}{R}_{li}^{j}+{\Sigma }_{li}^{j}\). The \({\widehat{h}}_{li}^{j}\) and \({\tilde{h }}_{li}^{j}\) are correlated.

In EW-MMSE estimation, estimation of every single element is carried out by processing signal received at each antenna and after that statistics are computed as result. It is noticeable that if off the diagonal elements are zero in covariance matrices then EW-MMSE performs same way as MMSE with lesser computational efforts.

5.3 LS Channel Estimator

There can be a case, when BS does not have any kind of statistical information, in such cases Bayesian estimator are useless and non Bayesian estimator is suitable substitute. The LS estimation is one of these kinds of estimation methods by which \({h}_{li}^{j}\) channel can be estimated during propagation (Özdogan et al. 2019, p. 3; Björnson et al. 2017, p. 268). The \({\widehat{h}}_{li}^{j}\) is LS estimation, which minimize \({\Vert {y}_{jli}^{p}- \sqrt{{P}_{li}}{\tau }_{P}{\widehat{h}}_{li}^{j}\Vert }^{2}\) and expressed as,

$${\widehat{h}}_{li}^{j}= \frac{1}{\sqrt{{P}_{li}}{\tau }_{P}}{y}_{jli}^{p}$$
(15)

In LS estimation, channel estimation \({\widehat{h}}_{li}^{j}\) and estimation error \({\tilde{h }}_{li}^{j}\) are correlated random variables, distributed as per below,

$${\widehat{h}}_{li}^{j} \sim {\mathcal{N}}_{\mathbb{C}} \left(\frac{1}{\sqrt{{P}_{li}}{\tau }_{P}}{\overline{y} }_{jli}^{p}, \frac{1}{{P}_{li}{\tau }_{P}}{{\Psi }_{li}^{j}}^{-1}\right)$$
(16)
$${\tilde{h }}_{li}^{j}\sim {\mathcal{N}}_{\mathbb{C}} \left({\overline{h} }_{li}^{j}- \frac{1}{\sqrt{{P}_{li}}{\tau }_{P}}{\overline{y} }_{jli}^{p}, \frac{1}{{P}_{li}{\tau }_{P}}{{\Psi }_{li}^{j}}^{-1}-{R}_{li}^{j}\right)$$
(17)

From Eqs. (11), (12) and (15), it is evident that LS channel estimation is simple and less computationally complex than MMSE and EW-MMSE, but it comes at cost of more complex channel estimation statistics a LS estimation have, compared to MMSE and EW-MMSE, which is seen from Eqs. (9), (10), (13), (14), (16) and (17). The non zero mean of \({\tilde{h }}_{li}^{j}\) in Eq. (17) confirm the compromise in communication quality, when LS estimation is used.

Also, from Eqs. (6), (12) and (15), it can be confirmed as said previously, that the MMSE estimation required full statistical distribution knowledge (\({\overline{h} }_{li}^{j}\) and \({R}_{li}^{j}\)), the EW-MMSE estimation required partial statistical distribution knowledge (\({\overline{h} }_{li}^{j}, {D}_{li}^{j}, \mathrm{and} {\Lambda }_{li}^{j}\)) and the LS estimation required no statistical distribution knowledge.

6 DL Spectral Effiency Using MR Precoding

The DL data transmissions are \({\tau }_{d}\) in each coherent slot, where the signal transmitted from BS l is

$${\mathrm{x}}_{l}= \sum\nolimits_{k = 1}^{{k}_{l}}{w}_{lk}{\varsigma }_{lk}$$
(18)

where \({\varsigma }_{lk} \sim {\mathcal{N}}_{\mathbb{C}} \left(0, {\rho }_{lk}\right)\) is the data signal transmitted from BS l for intended UE k in DL and \({\rho }_{lk}\) is the signal power. The \({w}_{lk}\) is the transmit precoding vector for spatial diversity determination. The \({w}_{lk}\) satisfies \({\mathbb{E}}\left\{{|\left|{w}_{lk}\right||}^{2}\right\}= 1\), such that the transmit power allocated to UE k is \({\mathbb{E}}\left\{{\left||\left|{w}_{lk}{\varsigma }_{lk}\right||\right|}^{2}\right\} = {\rho }_{lk}\). The received signal \({y}_{jk }\in {\mathbb{C}}\) at UE k in cell j is,

$${y}_{jk }={\left({h}_{jk}^{j}\right)}^{H}{w}_{jk}{\varsigma }_{jk}+ \sum\nolimits_{\begin{array}{c}k=1\\ i\ne k\end{array}}^{{K}_{j}}{\left({h}_{jk}^{j}\right)}^{H}{w}_{jk}{\varsigma }_{jk}+ \sum\nolimits_{\begin{array}{c}l=1\\ l \ne j\end{array}}^{L}\sum\nolimits_{i=1}^{{K}_{l}}{({h}_{jk}^{l})}^{H}{w}_{li}{\varsigma }_{li}+ {n}_{jk} $$
(19)

where \({n}_{jk} \sim (0,{\sigma }_{\mathrm{dl}}^{2})\) is independent and identically distributed additive receiver noise. In Eq. (19), first, second and third terms are respectively the desire signal, the intra-cell interference and the inter-cell interference. The ergodic DL capacity of UE k in cell j is lower bounded by (Björnson et al. 2017, p. 276),

$${SE}_{jk}^{dl}= \frac{{\tau }_{d}}{{\tau }_{c}}{\mathrm{log}}_{2}\left(1+ {\gamma }_{jk}^{dl}\right) \,\,\text{ bit/s/Hz}$$
(20)

where \({\gamma }_{jk}^{dl}\) is effective SINR can be expressed as,

$${\gamma }_{jk}^{dl}= \frac{{\rho }_{jk }{\left|{\mathbb{E}}\{{\mathrm{w}}_{jk}^{H}{h}_{jk}^{j}\}\right|}^{2}}{\sum_{l=1}^{L}\sum_{i=1}^{{K}_{l}}{\rho }_{li}{\mathbb{E}}\left\{{\left|{\mathrm{w}}_{li}^{H}{h}_{jk}^{l}\right|}^{2}\right\} - {\rho }_{jk}{\left|{\mathbb{E}}\{{\mathrm{v}}_{jk}^{H}{h}_{jk}^{j}\}\right|}^{2}+ {\sigma }_{\mathrm{dl}}^{2}}$$
(21)

where the expectations are taken from all sources of randomness.

However, the effective SINR \({\gamma }_{jk}^{dl}\) in Eq. (21) can be computed using MR precoding and different estimation methods for DL.

7 Basic Setup and Configuration

The coverage area is assumed of having 16 equal sized cells, where each cell area is 250 m × 250 m having square shape. Also the wrap around topology has been assumed to have equal interference from all directions to the BS. The UEs per cell are considered 10, where distribution of UEs is independent and uniform. Also it is taken care of minimum 35 m distance between UE and BS, while assuming UEs locations. The criterion to assign UE to particular BS among number of BSs options is the channel gain between UE and that selected BS should be largest. The UE location decides large scale fading and nominal angle. The antennas at BS are uniformly and linearly distributed (ULA), where distance between two consecutive antennas are assumed half wave-length.

The average channel response between UE i and BS j in cell l is expressed as (Björnson et al. 2017, p. 181),

$${\overline{h} }_{li}^{j} = \sqrt{{\beta }_{li}^{j,LoS} {[1 {e}^{j2\pi {d}_{H}\mathrm{sin}({\varphi }_{li}^{j})} \dots {e}^{j2\pi {d}_{H}(M-1)\mathrm{sin}({\varphi }_{li}^{j})}]}^{T}}$$
(22)

where the \({\beta }_{lk}^{j,LoS}\) is the large scale fading co-efficient, \({d}_{H}\) \(\le \frac{\lambda }{2}\) is the two consecutive antenna spacing, and \({\varphi }_{lk}^{j}\) is the angle of arrival (AoA) at UE. In Eq. (22), the co-efficient of large scale fading is defined as \({\beta }_{lk}^{j,LoS}=\frac{1}{{M}_{j}}{\Vert {\overline{h} }_{li}^{j}\Vert }^{2}\), where it is finite for any \({M}_{j}\) BS antennas. The \({\overline{h} }_{li}^{j}\) in Eq. (22) also represents direct propagation component (LoS). The NLoS propagation is approximately represented by covariance matrix as shown in Eq. (23) below,

$${\left[{R}_{li}^{j}\right]}_{s,m}= \frac{{\beta }_{li}^{j,NLoS}}{N}\sum_{n=1}^{N}{e}^{j\pi \left(s-m\right)\mathrm{sin}({\varphi }_{li,n}^{j})}{e}^{{-\frac{{\sigma }_{\varphi }^{2}}{2} \left(\pi \left(s-m\right)\mathrm{cos}({\varphi }_{li,n}^{j})\right)}^{2}}$$
(23)

where N is the number of scattering clusters, \({\beta }_{lk}^{j,NLoS}\) is the large scale fading co-efficient for NLoS, \({\varphi }_{li,n}^{j} \sim \mathcal{U} [{\varphi }_{li}^{j}-{40}^{o}, {\varphi }_{li}^{j}+{40}^{o} ]\) is the nominal AoA, \({\sigma }_{\varphi }\) is the angular standard deviation (ASD) from the nominal angel, n is the cluster number, s is row number and m is column number of \({R}_{li}^{j}\) matrix. Here the Gaussian local scattering model (Özdogan et al. 2019, p. 10; Björnson et al. 2017, p. 300) is considered for the covariance matrix \({\left[{R}_{li}^{j}\right]}_{s,m}\) of each cluster. The number of scattering clusters N = 6, the ASD\({\sigma }_{\varphi }={5}^{\mathrm{o}}\), the channel bandwidth for communication is 20 MHz, the total receive noise power is −94 dBm, the samples per each coherence slot is 200 and the pilot (per UE) in each cell is 10 assumed. The pilots are assigned randomly to the UEs.

As per 3GPP model (3GPP Tech. Report 2020, 26), the LOS probability between UE and BS is modelled, as per below,

$${\text{Probability\,\, of\,\, LoS}} = \left\{\begin{array}{c}\frac{300 - {d}_{li}^{j}}{300}, {0<d}_{li}^{j}<300\,{\text{m}},\\ 0 ,{d}_{li}^{j}>300\,{\text{m}}\end{array}\right.$$
(24)

It is evident from Eq. (23) that the distance between UE and BS is the only controlling parameter of LoS probability. In existence of LoS, the corresponding large scale fading coefficient is modelled as (3GPP Tech. Report 2020, 17),

$${\beta }_{li}^{j}= -30.18-26 {\mathrm{log}}_{10}\left({d}_{li}^{j}\right)+ {F}_{li}^{j}\,\, \text{{dB}}$$
(25)

where \({F}_{li}^{j}\sim \mathcal{N}\)(0, \({\sigma }_{sf}^{2}\)) with \({\sigma }_{sf}=4\), is shadow fading co-efficient. In absence of LoS, the corresponding large scale fading coefficient is modelled as (3GPP Tech. Report 2020, 17),

$${\beta }_{li}^{j}= -34.53-38 {\mathrm{log}}_{10}\left({d}_{li}^{j}\right)+ {F}_{li}^{j}\,\,\text{{dB}}$$
(26)

where \({F}_{li}^{j}\sim \mathcal{N}\)(0, \({\sigma }_{sf}^{2}\)) with \({\sigma }_{sf}=10\), is shadow fading co-efficient. The Rician factor is modeled as (3GPP Tech. Report, 2020, 26), \({k}_{li}^{j}=13-0.03{d}_{li}^{j}\) [dB], which is used to calculate \({\beta }_{li}^{j,LoS}\) and \({\beta }_{li}^{j,NLoS}\) as shown below in Eq. (25).

$${\beta }_{li}^{j,LoS}= \sqrt{\frac{{k}_{li}^{j}}{{k}_{li}^{j}+1 }}{\beta }_{li}^{j} \,\,{\text{and}}\,\,{\beta }_{li}^{j,NLoS}= \sqrt{\frac{1}{{k}_{li}^{j}+1 }}{\beta }_{li}^{j}$$
(27)

The calculated \({\beta }_{li}^{j,LoS}\) and \({\beta }_{li}^{j,NLoS}\) are used in Eq. (22) and (23) respectively. Also over all large scale fading coefficient can be expressed as,

$${\beta }_{li}^{j}= {\beta }_{li}^{j,LoS}+{\beta }_{li}^{j,NLoS},$$
(28)

In LTE systems, UEs at the cell edge are allowed to transmit at maximum power and by gradually reducing the power for UEs that are located closer to the BS. The same policy adopted here for UL transmission, because the UL powers affect not only the UL data transmission but also the quality of the channel estimates and indirectly the combining vectors. So to provide fair power allocation to UEs, UL power control policy decided by heuristic approach as below as per (Björnson et al. 2017, p. 464),

$$p_{jk} = \left\{ \begin{aligned} & p_{max}^{ul} ~,\Delta > \frac{{\beta _{jk}^j }}{{\beta _{j,min}^j }}, \\ & p_{max}^{ul} \Delta \frac{{\beta _{j,min}^j }}{{\beta _{jk}^j }},\Delta \le \frac{{\beta _{jk}^j }}{{\beta _{j,min}^j }}~, \\ \end{aligned} \right.$$
(29)

where \({p}_{jk}\) is the transmit power, the \({p}_{max}^{ul}\) is maximum UL power with value 10 dBm and minimum large scale fading coefficient defined as \({\beta }_{j,min}^{j}=\mathrm{min}({\beta }_{j1}^{j},\dots {\beta }_{jk}^{j}\dots ,{\beta }_{jK}^{j})\). The weakest channel UEs can radiate with full power and power radiation decreased proportional to channel strength increment. The policy adopted also for DL as it is for UL for simplicity.

8 Output Results

In this section, simulation is carried out for SE as per above SE equations using MATLAB®.

Fig. 1.
figure 1

Averaged Sum DL SE Vs. No. of BS antennas in spatially correlated fading, where k = 10.

Full size image

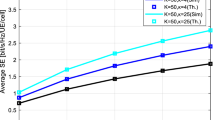
The Fig. 1 shows sum SE in DL as function of numbers of BS antennas, averaged over number of realization of various shadow fading and UE locations. The SE carried out for MR precoding, MMSE, EW-MMSE, and LS estimation methods in correlated fading scenario. The SE carried out for Rician and Rayleigh spatially correlated fading. Also SE carried out analytically from equations and practically from Monte Carlo based simulations, where square marker plots indicates Monte-Carlo based simulation and remaining are analytical simulation based plots. The overlapping or closeness of analytical plots (from closed form equations) with practical plots (from Monte-Carlo simulation) validates the carried out results. The DL SE using MMSE estimator is highest in correlated Rician fading case because of acquiring full channel statistics by MMSE estimators, where as DL SE using LS estimation is lowest in same case because of not acquiring channel statistics by LS estimator. The DL SE using EW-MMSE estimator is lower than MMSE but higher than LS estimator in correlated Rician fading case because of acquiring partial channel statistics (diagonals of covariance matrices and average channel gains only). However performance of EW-MMSE is more closer to MMSE because all channel statistics are acquired (as like MMSE) except off diagonal elements of covariance matrices only and in correlated Rician fading case contribution of off diagonal elements of covariance matrices is very less compared to diagonal elements for over all estimation quality. The SE gap between LS and MMSE/EW-MMSE is increasing proportional BS antennas, as LS estimator does not acquiring any type of channel statistics. In Rayleigh fading scenario, DL SE using MMSE estimator is highest compared to EW-MMSE and LS estimators, whereas DL SE of EW-MMSE and LS estimator is identical. The average channel gains and diagonal elements of covariance matrices are significant channel statistics for LoS component of channel propagation. However in Rayleigh fading case, due to lack of strong LoS channel propagation, statistical knowledge of average channel gains and diagonal elements of covariance matrices is not available for over all estimation process. So channel statistics acquirement efforts by EW-MMSE in Rayleigh fading case are worthless and estimation quality of EW-MMSE and LS estimators results identical, which can be seen in Fig. 1. The MMSE estimator gives best performance in correlated Rician or Rayleigh fading scenarios.

Fig. 2.
figure 2

CDF Vs. DL SE per UE in different fading scenario, where k = 10 & M = 100.

Full size image

The Fig. 2 shows CDF of SE per UE, where random UE locations and shadow fading realisations introduce randomness. It is seen from Fig. 2 that the probability to have SE per UE is higher in Rician fading case compared to Rayleigh fading case. In Rician fading case, for good channel condition the probability of SE per UE is almost equal for MMSE and EW-MMSE, since estimation errors are small. However the difference of probability of SE per UE can be noticed between MMSE and EW-MMSE for weak channel conditions. The good channel condition is defined as having higher probability of SE per UE and weak channel condition is defined as having lower probability of SE per UE. The probability of SE per UE is lowest for LS estimator in Rician fading case for all values of SE per UE. It is noticeable from Fig. 2 that the probability of SE per UE is highest of MMSE compared to other two estimators at very weak channel condition (SE per UE is less than or equal to 0.3 bit/s/Hz) in Rician or Rayleigh fading case. Even for given channel having SE per UE is less than or equal to 1.4 bit/s/Hz, the corresponding probability of SE per UE is higher of MMSE in Rayleigh fading compared to LS in Rician. However, as in Rician, the probability of SE per UE of MMSE is highest in Rayleigh fading case also as shown in Fig. 3, whereas the probability of SE per UE of EW-MMSE and LS estimators is almost equal in Rayleigh fading case.

Fig. 3.
figure 3

Averaged Sum DL SE Vs. No. of antennas at BS in spatially uncorrelated fading, where k = 10.

Full size image

The Fig. 3 shows sum DL SE as function of number of antennas at BS, averaged over number of realization of various shadow fading and user equipment locations. The SE carried out for different estimation methods like MMSE, EW-MMSE, and LS in uncorrelated fading scenario, using same MR precoding transmission method. The DL SE of MMSE and EW-MMSE is identical for uncorrelated Rician fading case as shown in Fig. 3. The only off diagonal elements of covariance matrices are not estimated in EW-MMSE compared to MMSE estimator, reaming estimation part is same for both estimators. However in uncorrelated fading case, off diagonal elements of covariance matrices are zero, so the estimates of MMSE and EW-MMSE are identical. Further, the SE using LS estimator is lower than MMSE/EW-MMSE estimator for uncorrelated Rician fading case, since LS estimator does not utilising and acquiring any type of statistical knowledge of channel. In case of uncorrelated Rayleigh fading, average channel gain (represent the LoS component of channel propagation) and covariance matrices estimation efforts are useless since absence of LoS and covariance matrices are unitary matrices. So all estimates using MMSE, EW-MMSE and LS estimators are same up to deterministic scaling factor and DL SE using same three estimators is same.

9 Conclusion

The average sum DL SE has been discussed throughout for correlated/uncorrelated Rician and Rayleigh fading scenarios in the multi-cell Massive MIMO system. However, MR precoding method is used for DL transmission and DL SE comparison has been carried out for MMSE, EW-MMSE and LS estimation methods. The closed form achievable SE expressions provide insight detailed view of the processing and interference nature. It is observed throughout that the existence of the LoS propagation along with NLoS propagation (like Rician fading) can improve the DL SE compared to the NLoS propagation only (Rayleigh fading). The performance of MMSE and EW-MMSE estimators is identical in all fading scenarios except correlated Rician fading case, where the performance gap is also small. However computational complexity is lower in EW-MMSE compared to MMSE estimator. The performance gap between MMSE/EW-MMSE and LS is comparatively large in all fading scenarios except uncorrelated Rayleigh fading case, where the performance of all three estimators is identical. However LS estimator has lowest computational complexity, but performance is very poor. So in general, MMSE is the best without computational complexity constraint and EW-MMSE is the optimum with computation complexity constraint. In summary, the spatial channel correlation plays important role in choice of optimum estimator. Also the existing performance gap between MMSE/EW-MMSE and LS estimators increases with increase in number of BS antennas as seen from output results. At last in practical scenario, as channel statistics are not fully and perfectly known, the upper and lower performance boundaries are almost set by MMSE/EW-MMSE and LS estimators respectively.