Self-distilled Self-supervised Depth Estimation in Monocular Videos

Abstract

In this work, we investigate approaches to leverage self-distillation via predictions consistency on self-supervised monocular depth estimation models. Since per-pixel depth predictions are not equally accurate, we propose a mechanism to filter out unreliable predictions. Moreover, we study representative strategies to enforce consistency between predictions. Our results show that choosing proper filtering and consistency enforcement approaches are key to obtain larger improvements on monocular depth estimation. Our method achieves competitive performance on the KITTI benchmark.

1 Introduction

Depth estimation is an essential task used in a wide range of applications in computer vision, for instance, 3D modeling, virtual and augmented reality, and robot navigation. Depth information can be obtained using sensors such as LIDAR or RGB-D cameras. However, in some scenarios, we cannot rely solely on them due to their limited range and operating conditions. Thus, alternative approaches such as estimating depth from images become more appealing. Supervised deep learning methods for depth estimation have shown impressive results. However, these approaches depend on the expensive acquisition of high-quality ground-truth depth data for training.

In contrast, self-supervised depth estimation approaches do not require ground-truth. Since the only inputs required are stereo images or monocular sequences, they can be trained on diverse data sets without depth labels. Self-supervised methods leverage geometric priors to learn image reconstruction as an auxiliary task. Depth maps are obtained as an intermediary result of the image reconstruction process.

Several works have shown that self-supervised depth estimation can be benefited from learning additional auxiliary tasks, for example, self-distillation. Self-distillation methods aim to improve a model performance by distilling knowledge from the model itself. An interesting strategy for performing self-distillation consists in extracting information from distorted versions of the input data by enforcing consistency between their predictions [26]. In this work, we propose a self-distillation approach via prediction consistency to improve self-supervised depth estimation from monocular videos. Since enforcing consistency between predictions that are unrealiable cannot provide useful knowledge, we propose an strategy to filter out unreliable predictions. Moreover, the idea of enforcing consistency between predictions has been widely explored in self-distillation [8, 18, 27] and semi-supervised learning [1, 13, 20,21,22, 24]. In order to explore the space of consistency enforcement strategies, we adapt and evaluate representative approaches on the self-supervised depth estimation task.

In summary, the main contributions of our work are the following: (i) the proposition of a multi-scale self-distillation method based on prediction consistency, (ii) the design of an approach to filter unreliable per-pixel predictions on the pseudo-labels used in self-distillation, and (iii) the exploration and adaptation of several consistency enforcement strategies for self-distillation. To validate our method, we show a detailed evaluation and a comparison against state-of-the-art methods on the KITTI benchmark. Our code is available at https://github.com/jmendozais/SDSSDepth.

2 Related Work

Self-supervised Depth Estimation. The main intuition of self-supervised depth estimation methods is to leverage multi-view geometry relations computed from depth and camera motion predictions to reconstruct one view with the pixel values from another view. Depth and camera motion can be obtained from deep networks that are trained by minimizing the reconstruction error. Garg et al. [9] used this intuition to train a depth network using stereo pairs as views. Similarly, Zhou et al. [29] proposed a method to obtain the views from monocular sequences and used deep networks to estimate relative pose and depth maps. Several works addressed limitations of these methods such as inaccurate prediction in occluded regions [16] and regions with moving objects [2, 12]. Other works aim to improve the learning signal by enforcing consistency between several representations of the scene [3, 16, 17] or by using auxiliary tasks such as semantic segmentation or self-distillation [14, 15]. Similarly to [14], our method leverages self-distillation to improve depth estimation. Unlike prior work, we focus on exploring representative strategies to distill knowledge from the predictions of our model.

Pseudo-labeling Approaches for Self-supervised Depth Estimation. Many self-supervised methods trained from stereo images [23, 25] or monocular sequences [4, 5, 14, 15, 23] rely on pseudo-labels to provide additional supervision for training their depth networks. These methods can use state-of-the-art classical stereo matching algorithms [23], external deep learning methods [4, 5], or their own predictions [25] to obtain pseudo-labels. Since the quality of the pseudo-labels is not always guaranteed, methods filter out unreliable per-pixel predictions based on external confidence estimates [4, 5, 23] or uncertainty estimates that are a result of the method itself [25]. Additionally, some methods leverage multi-scale predictions for creating pseudo-labels by using the predictions at the highest-resolution as pseudo-labels to supervise predictions at lower resolutions [28] or by selecting, per pixel, the prediction with the lowest reconstruction error among the multi-scale predictions [19].

We focus on methods that use their own prediction as pseudo-labels. For example, Kaushik et al. [14] augmented a self-supervised method by performing a second forward pass with strongly perturbed inputs. The predictions from the second pass are supervised with predictions of the first pass. Liu et al. [15] proposed to leverage the observation depth maps predicted from day-time images are more accurate than predictions from night-time images. They used predictions from day-time images as pseudo-labels and train a specialized network with night-time images synthesized using a conditional generative model.

Self-distillation. These methods let the target model leverage information from itself to improve its performance. An approach is to transfer knowledge from an instance of the model, previously trained, via predictions [8, 18, 27] and/or features to a new instance of the model. This procedure could be repeated iteratively. Self-distillation has a regularization effect on neural networks. It was shown that, at earlier iterations, self-distillation reduces overfitting and increases test accuracy, however, after too many iterations, the test accuracy declines and the model underfits [18].

Self-distillation has been extensively explored, mainly in image classification problems. An approach performs distillation by training instances of a model sequentially such that a model trained on a previous iteration is used as a teacher for the model trained in the current iteration [8]. Similarly, Yang et al. [27] proposed to train a model in a single training generation imitating multiple training generations using a cyclic learning rate scheduler and using the snapshots obtained at the end of the previous learning rate cycle as a teacher. Our work explores the idea of leveraging multiple snapshots in a single training generation on the self-supervised depth estimation problem.

Consistency Regularization. Enforcing consistency between predictions obtained from perturbed views of input examples is one of the main principles behind consistency regularization approaches on deep semi-supervised works. An early method [20] used this principle doing several forward passes on perturbed versions of the input data. Furthermore, other methods showed that the usage of advanced data augmentation perturbations [24] or a combination of a weak and strong data augmentation perturbation in a teacher-student training scheme [21] can be helpful to improve the resulting models.

Existing works showed that average models, i.e., models whose weights are the average of the model being trained at different training steps, can be more accurate [1, 13, 22]. Average models can be used, as teachers, to obtain more accurate pseudo-labels [1, 22]. Moreover, the use of cyclic learning rate schedulers can improve the quality of the models that are averaged and the resulting model at accuracy and generalization [13], as well as it can be adapted to the consistency regularization framework [1]. Similarly to [1], our method uses a cyclic cosine annealing learning rate schedule to obtain a better teacher model.

3 Depth Estimation Method in Monocular Videos

3.1 Preliminaries

Our method is built on self-supervised depth estimation approaches that use view reconstruction as main supervisory signal [29]. These approaches require to find correspondences between pixel coordinates on frames that represent views of the same scene. We represent this correspondences in Eq. 1.

$$\begin{aligned} x_{s} \sim \mathbf {K}\mathbf {T_{t \rightarrow s}} \mathbf {D_t} (x_t)\mathbf {K}^{-1}x_{t} \end{aligned}$$

(1)

We reconstruct the target frame using the correspondences and the pixel intensities in the source frame $\mathbf {\hat{I}_{\mathbf {s\rightarrow t}}}(x_t) = \mathbf {I_{\mathbf {s}}}(x_s)$. This process is known as image warping. This approach requires the dense depth map $\mathbf {D_t}$ of the target image, which we aim to reconstruct, the Euclidean transformation $\mathbf {T_{t\rightarrow s}}$, and camera intrinsics $\mathbf {K}$. Our model used to convolutional neural network to predict the depth maps and the Euclidean transformation, and assumes that the camera intrinsics are given. The networks are trained using the adaptive consistency loss $\mathcal {L}_{ac}$. We refer the reader to [17] for a detailed explanation.

3.2 Self-distillation via Prediction Consistency

The core idea of self-distillation based on prediction consistency is to provide additional supervision to the model by enforcing consistency between the depth map predictions obtained from different perturbed views of an input image. Our self-distillation approach applies two different data augmentation perturbations to an input snippet. To use less computational resources, we use snippets of two frames $\mathcal {I} = \{\mathbf {I_t}, \mathbf {I_{t+1}}\}$. The model predicts the depth maps for all images in the input snippet. Since we need to apply two data augmentation perturbations, we have two depth maps for each frame in the snippet. Then, we enforce consistency by minimizing the difference between the predicted depth maps for each frame.

There are several approaches to enforce consistency between prediction. The simplest variation of our method use the pseudo-label approach. It considers one of depth maps as pseudo-label $\mathbf {D^{(pl)}}$, which implies that gradients are not back-propagated through it, and the other depth map as prediction $\mathbf {D^{(pred)}}$. In Sect. 3.4, we improve our method considering other consistency enforcement strategies. Moreover, we enforce prediction consistency using the mean squared error (MSE) as difference measure. In addition, we filter the unreliable depth values on the pseudo-label using a composite mask. Equation 2 shows the self-distillation loss term for a snippet $\mathcal {I}$.

$$\begin{aligned} \mathcal {L}_{sd} = \frac{1}{|\mathcal {I}|}\sum _{\mathbf {I_k} \in \mathcal {I}} \frac{1}{|\mathbf {M_k^{(c)}}|} \sum _{x \in \varOmega (\mathbf {I_k})} \mathbf {M_k^{(c)}}(x)\dot{\Big (}\mathbf {D_k^{(pl)}}(x) - \mathbf {D_k^{(pred)}}(x)\Big )^2 \end{aligned}$$

(2)

where $\mathbf {I_k}$ is a frame in the snippet and $\mathbf {M_k^{(c)}}$ is its composite mask, $\varOmega (\mathbf {I_k})$ is the set of pixel coordinates, and $\mathbf {D_k^{(pl)}}$ and $\mathbf {D_k^{(pred)}}$ represent the pseudo-label and predicted depth maps, respectively.

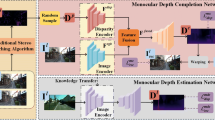
Since our model predicts the depth maps at multiple scales, we compute the self-distillation loss for each scale. We assume that the pseudo-label at the finest scale is more accurate than the pseudo-labels at coarser scales. Thus, we only use the finest pseudo-label. We upscale the predictions to the finest scale to match the pseudo-label scale. Finally, we compute the self-distillation loss for each scale. Figure 1 depicts our self-distillation approach.

Fig. 1.

Overview of our method. The self-distillation component leverages the multi-scale predictions obtained from the view reconstruction component. The predictions are upscaled to the finest resolution. More accurate predictions are obtained from the teacher model. The teacher predictions at the finest resolution are used as pseudo-labels to improve the predictions obtained from view reconstruction.

3.3 Filtering Pseudo-labels

We noticed empirically that unreliable depth prediction produces very large differences between pseudo-labels and predictions. These very large differences make training unstable and do not allow the model to converge randomly. We address this problem by excluding pixels with very large differences using a threshold value. In this section, we present two schemes to determine the threshold.

In the first scheme, we compute the threshold as a percentile P on the pseudo-label and prediction differences for all pixels in a batch of snippets. Then, we create valid mask considering as valid all the pixels with differences smaller than the threshold, as shown in Eq. 3.

$$\begin{aligned} \mathbf {M}^{(p)}(x) = \big [\big (\mathbf {D^{(pl)}}(x) - \mathbf {D^{(pred)}}(x)\big )^2 < P\big ] \end{aligned}$$

(3)

where [.] denotes the Iverson bracket operator. The final mask is obtained combining the latter mask with the compound mask. The final mask could be expressed as $\textbf {M} = \textbf {M}^{(p)} \odot \textbf {M}^{(c)}$, where $\odot$ represents the element-wise product. Finally, we replace $\mathbf {M}^{(c)}$ with $\mathbf {M}$ in Eq. 3.

We believe that the idea of using a threshold obtained from the distribution of differences by batch might be detrimental because we do not take into consideration that batches with reliable predictions should have thresholds that exclude less pixels than the threshold used on batches with more unreliable predictions.

In the second scheme, we address this limitation by approximating a global threshold $P^{\text {(EMA)}}$ using the exponential moving average (EMA) of the percentile values for each batch during training. Another advantage of using a moving average is that we take into consideration that the distribution of depth differences change during training. This means that, when the depth differences become smaller during training, the threshold changes by increasing the weight of the percentiles from latter batches on the average. Equation 4 shows our global threshold approximation.

$$\begin{aligned} P_t^{\text {(EMA)}} = P_{t-1}^{\text {(EMA)}} \cdot \beta + P_t \cdot (1 - \beta ) \end{aligned}$$

(4)

where $P_t$ is the threshold computed from the batch at the t training iteration, $P_t^{\text {(EMA)}}$ is threshold obtained using the EMA at the t training iteration, and $\beta$ controls the influence of the previous moving average percentile and the current percentile into the computation of the current threshold. Similarly to the first scheme, we compute a valid mask $\mathbf {M}^{\text {(EMA)}}$using $P^{\text {(EMA)}}$, we combine this mask with the compound mask $\mathbf {M} = \mathbf {M}^{{\rm {(EMA)}}} \odot \mathbf {M}^{(c)}$ and, finally, we use $\mathbf {M}$ instead of $\mathbf {M}^{(c)}$ in Eq. 2.

3.4 Consistency Enforcement Strategies

In previous sections, we used a pseudo-label strategy to enforce consistency between depth predictions. Here, we describe representative consistency enforcement strategies adapted to our self-distillation approach. Figure 2 depicts these consistency enforcement strategies. We named each strategy similarly to the methods that introduced the key idea into external domains [1, 13, 20, 22]. Similarly to the pseudo-label strategy, variants of our method that use the strategies described in this section also adopt the second scheme described in Sect. 3.3 to filter out unreliable per-pixel predictions before computing the predictions difference.

Fig. 2.

Simplified views of the consistency enforcement strategies. S denotes the input snippet, Aug 1 and Aug 2 denote two perturbed views of the input snippet, T denotes the camera motion transformation, D1 and D2 denote depth maps predictions, $L_{ac}$ denotes the adaptive consistency loss, $L_{sd}$ denotes the self-distillation loss, and red lines mark connections where the gradients are not back-propagated. (Color figure online).

$\mathbf {\Pi }$-Model. Similarly to the pseudo-label approach, this strategy consists in enforcing consistency between prediction from two perturbed views of the same input. In contrast with the pseudo-label approach, the gradients are back-propagated through both predictions.

Mean Teacher. Instead of using the same depth network to generate the pseudo-labels and the predictions, we can introduce a teacher network that can potentially predict more accurate pseudo-labels, and provide better supervisory signal to the model currently being trained, the student network. In this approach, the teacher depth network weights are the EMA of the depth network weights in equally spaced training iterations.

Stochastic Weight Averaging. Similarly to the mean teacher strategy, we set the teacher depth network weights as the EMA of the depth network weights. In contrast, the training process is split into several cycles. At each cycle, the learning rate decreases and the teacher depth network is updated with the weights of depth network at the end of the last epoch of each training cycle, where the learning rate reaches its lowest value.

In the first generation of the training process, we use the student network to predict pseudo-label. Once the model has converged to a proper local optimum, we use its weights to initialize the teacher network. Then, in the following cycles, the training process mimics multiple training generations using a cyclic cosine annealing learning rate. At the end of each cycle, when the learning rate reaches its lowest value, and model likely converged to a good local optimum, we update the weights the teacher network using EMA with the student network weights.

3.5 Additional Considerations

Final Loss. The overall loss is a weighted sum of our self-distillation loss $\mathcal {L}_{sd}$, adaptive consistency loss $\mathcal {L}_{ac}$ [17], depth smoothness loss $\mathcal {L}_{ds}$, translation consistency loss $\mathcal {L}_{tc}$, and rotation consistency loss $\mathcal {L}_{rc}$. The rotation and translation consistency losses are similar to the cyclic consistency loss defined in [12]. In contrast, our translation consistency loss only considers camera motion. Equation 5 shows our final loss.

$$\begin{aligned} \mathcal {L} = \sum _{i \in \mathcal {S}} \frac{1}{2^i}\Big (\mathcal {L}_{ac}^{(i)} + \lambda _{ds} \mathcal {L}_{ds}^{(i)} + \lambda _{sd} \mathcal {L}_{sd}^{(i)} \Big ) + \lambda _{rc} \mathcal {L}_{rc} + \lambda _{tc} \mathcal {L}_{tc} \end{aligned}$$

(5)

where $\mathcal {S}$ is the set of scales and $\lambda _{sd}$, $\lambda _{ds}$ $\lambda _{rc}$, $\lambda _{tc}$ is the weight of the self-distillation, depth smoothness, rotation consistency, and translation consistency loss terms, respectively.

4 Evaluation

4.1 Experimental Setup

Dataset. We use the KITTI benchmark [10]. It is composed of video sequences with 93 thousand images acquired through high-quality RGB cameras captured by driving on rural areas and highways of a city.

We used the Eigen split [6] with 45023 images for training and 687 for testing. Moreover, we partitioned the training set on 40441 for training, 4582 for validation. For result evaluation, we used the standard metrics.

Training. Our networks are trained using ADAM optimization algorithm using $\beta _1$ = 0.9, $\beta _2$ = 0.999. We used the batch size of 4 snippets. We use 2-frame snippets unless otherwise specified. We resize the frames to resolutions of 416 $\times$ 128 pixels unless otherwise specified.

The training process is divided into three stages. In the first stage, we train the model with the self-distillation loss disabled. The model is trained using a learning rate of $1e-4$ during 15 epochs, and then its reduced to $1e-5$ during 10 additional epochs. In the second stage, we train the model with self-distillation term enabled. The model is trained with a learning rate of $1e-5$ during 10 additional epochs. Finally, in the third stage, we train the model enabling SWA teacher for the depth network with a cyclical cosine learning rate schedule with an upper bound of $1e-4$, a lower bound of $1e-5$, and using 4 cycles of 6 epochs each, unless otherwise specified.

4.2 Self-distillation via Prediction Consistency

Table 1 shows the results with the simplest variant of our self-distillation approach. The results show a consistent improvement when self-distillation loss is used. The model trained with self-distillation loss outperforms the baseline at all error metrics and almost all accuracy metrics.

When searching for the optimal weight $\lambda _{sd}$ for the self-distillation term, we noticed that large $\lambda _{sd}$ values allow to obtain good results. However, due to large depth differences, the model diverges on some executions. Due to this instability, we use a smaller $\lambda _{sd} = 1e2$. This observation motivated us to explore approaches to filter unreliable predictions.

Table 1. Comparison of the baseline model and the variation of our method that uses the pseudo-label strategy.

4.3 Filtering Pseudo-labels

Table 2 shows that our two filtering strategies outperform that variation of our method does not use any additional filtering approach other than the composite mask in the majority of error and accuracy metrics. Moreover, the results show that the approach that uses the EMA of the percentiles to estimate the threshold is better than using only the percentile of each batch.

Table 2. Comparison of variants of our method with and without filtering strategies. P denotes that we filtered pseudo-labels using a percentile by batch as thresholds, and $P^{\text {(EMA)}}$ denotes that we filtered pseudo-labels using a threshold that is the EMA computed from percentiles of the batches during training iterations.

4.4 Consistency Enforcement Strategies

Table 3 shows that, regardless the consistency enforcement strategy, self-distillation via prediction consistency can improve the performance of our baseline model. Moreover, the results show that the variant that uses SWA strategy outperforms the other consistency enforcement strategies in most of the error and accuracy metrics. This variant is used as our final model. Some qualitative results are illustrated in Fig. 3.

Table 3. Comparison of the representative consistency enforcement strategies. PL denotes the pseudo-label, $\Pi$ M denotes the $\Pi$-Model, MT denotes the mean teacher, and SWA denotes the stochastic weight averaging strategy.

Fig. 3.

Qualitative results. Depths maps obtained using our final model.

4.5 State-of-the-Art Comparison

Table 4 shows a quantitative comparison with state-of-the-art methods. Our method outperforms methods that explicitly address moving objects such as [2, 3, 12]. Fang et al. [7] obtained better results due to the usage of VGG16 as encoder, which has 138 million parameters. In contrast, our method uses a smaller encoder ResNet-18, which has 11 million parameters. The results show that our method achieves competitive performance when compared to state-of-the-art methods.

Table 4. Results of depth estimation on the Eigen split of the KITTI dataset. We compared our results against several methods of the literature. To allow a fair comparison, we report the results of competitive methods trained with a resolution of 416 $\times$ 128 pixels. N.F. denotes the number of frames in the input snippet (*) indicates newly results obtained from an official repository. (-ref.) indicates that the online refinement component is disabled.

5 Conclusions

We showed that to take full advantage of self-distillation, we need to consider additional strategies, such as the filtering approaches we proposed in this work, to deal with unreliable predictions. We demonstrated that choosing a proper consistency enforcement strategy in self-distillation is important. Our results suggest that the features of consistency enforcement strategies, such as (i) enforcing teacher quality and (ii) enforcing difference between teacher and student network weights, which are embedded in the SWA strategy, are important to obtain larger improvements. We explored various strategies to benefit from self-distillation for self-supervised depth estimation when the input are monocular sequences. Moreover, we believe that our findings can provide useful insights to leverage self-distillation in methods that use stereo sequences as input, as well as semi-supervised and supervised methods.