Keywords

1 Introduction

A guard is defined as an entity capable of observing the terrain or sensing an event on the terrain. In real life, numerous guards are used for a variety of purposes. For example, forest fires are detected by watchtowers located on terrains [12], where watchtowers are considered as guards since, with the appropriate equipment, they can guard the terrain (to detect fires). It is important for military units to prevent any intrusion into their region of deployment. Military units achieve this by locating watch-posts on the terrain such that no dead zone exists [6]. In order to maintain effective communication, relay stations need to be placed on the terrain such that each station is visible from at least one other station [10]. As defined in Eliş [8], the goal in the Terrain Guarding Problem (TGP) is to locate a minimum number of guards on the terrain such that each point on the terrain is visible or guarded by at least one of the guards.

Real three-dimensional terrains need to be represented as mathematical objects to be able to solve TGP and to perform similar terrain-related analyses. A mathematical or a digital representation of a real terrain surface is known as a Digital Elevation Model (DEM) [9, 15]. Triangulated irregular network (TIN) is a preferred DEM since some important terrain features are preserved [9]. As described in Eliş [8], a TIN is obtained as follows. Suppose that \(S \in R^{3}\) is a real terrain surface. Points are sampled from S that we assume represent S sufficiently. Let P = {p1, …, pn} be the set of such points with x, y, and z coordinates. Let \(\overline{{p_{i} }} \in R^{2}\) be the projection of pi onto the x–y plane, and \(\overline{P} = \{ \overline{{p_{1} }}, \ldots,\overline{{p_{n} }} \}\) be the set of such points. The points sampled from S and their projections are referred to as vertices. The vertices in \(\overline{P}\) become the vertices of the triangles on the plane after the triangulation is performed [4]. Let us denote the triangulation by \(\overline{T}\). Next, each point \(\overline{{p_{i} }} \in \overline{P}\) is elevated to its real height together with the edges. The object obtained as such is a TIN (Fig. 8.1).

Fig. 8.1
An illustration of a large network in the shape of uneven triangles.

Triangulated irregular network (as illustrated in Church [2])

Full size image

In the following, we largely adopt the notation used in Eliş [6–8]. Let us denote TIN by T. We may assume that T is in the nonnegative orthant without loss of generality. Let g((x, y)) denote the height of the terrain at (x, y) and V be the visible region, i.e. V = {(x, y, z): \((x,y) \in \overline{T}\) and z ≥ g((x, y))}. The region below T is denoted by F. Let p1 and p2 ∈ R3 such that their projection is in \(\overline{T}\). The line segment LS(p1, p2) ≡ {p1 + \(\lambda\) (p2 − p1): \(\lambda \in [0,1]\)} connects p1 and p2. We say that p2 is visible from/guarded by p1 if LS(p1, p2) is a subset of V, and not visible from p1 if LS(p1, p2) ∩ F ≠ \(\varnothing\). A visibility function is defined as follows,

$$v\left( {\varvec{p}_{\mathbf{1}}, \varvec{p}_{\mathbf{2}} } \right) = v\left( {\varvec{p}_{\mathbf{2}},\varvec{p}_{\mathbf{1}} } \right) = \left\{ {\begin{array}{*{20}l} 1 & {\text{if LS}\left( {\varvec{p}_{\mathbf{1}}, \varvec{p}_{\mathbf{2}} } \right) \subseteq V} \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$

Let VS(x) denote the “viewshed” of p, i.e. \(VS(\varvec{x}) = \{ \varvec{y} \in T: v(\varvec{x},\varvec{y}) = 1\}\). Let X = {x1, …, xk} be a set of points on T. We say that X guards or covers T if every point on T is guarded by at least one of the guards located at points in X. A formal definition is given by the following function,

$$\varvec{VIS}\left( {\varvec{y},\varvec{X}} \right) = \left\{ {\begin{array}{*{20}l} {{1}}, & {{\text{if}}\,\exists \,{\varvec{x}}_{{\varvec{j}}} \in \,X,\, {\text{such that}}\, v\left( {\varvec{y}, \varvec{x}_{{j}} } \right) = 1} \\ {0,} & {{\text{otherwise}}} \\ \end{array} } \right.$$

In the Terrain Guarding Problem (2.5D TGP), the goal is to find a set \({\varvec{X}}\) such that X guards T and has the minimum cardinality. A formal definition is given as follows,

$$\begin{array}{*{20}l} {\left( {2.5{\text{D TGP}}} \right)} \hfill & {} \hfill \\ {{\text{Minimize}}} \hfill & {\left| {\varvec{X}} \right|} \hfill \\ {\text{Subject to}} \hfill & {{{{VIS} (\varvec{y},\varvec{X} ) = 1, }}\,\forall \,{\varvec{y}} \in {{T}}} \hfill \\ {} \hfill & {{\varvec{X}} \subseteq {\text{T}}} \hfill \\ \end{array}$$

For 1.5 D terrains, we adopt the notation used in Eliş [7]. 1.5D terrain (T′) is a profile of a 2.5D terrain along a line and is characterized by a piecewise linear curve (Fig. 8.2). The definition of 1.5D TGP is the same as 2.5D TGP except that the terrain is a 1.5-dimensional surface. 1.5D TGP has applications where street lights or security sensors are placed along roads, communication networks are constructed [1], or cameras/posts are located on the borderline [7].

Fig. 8.2
An illustration depicts 1.5-dimensional terrain. The labels listed are h, x set within parenthesis, T superscript ‘, V, F, 0, x, and L.

A 1.5 dimensional terrain

Full size image

As shown in Fig. 8.2, the terrain surface T′ is denoted by h(x), which gives the height of x \(\in\) [0, L]. Visibility and covering of a given point by another point or by a set of guards are defined as in 2.5D case. The formal definition of 1.5D TGP is the same as 2.5D except that the terrain is 1.5 dimensional.

2 Literature Review

2.1 2.5D TGP

The 2.5D TGP was first investigated by De Floriani et al. [5]. They showed that a set-covering formulation could be used to solve the TGP. In their study, the vertices of the triangles were used as potential guard locations, among which an optimal solution is sought. We note that in order for the solution obtained to be optimal, it is not sufficient to use an exact algorithm. In addition to using an exact algorithm, one also needs to prove that the set of guard locations is a finite dominating set (FDS). An FDS is a finite set of points that contains an optimal solution to an optimization problem with (possibly) an uncountable feasible set. Perhaps, the best-known FDS is the set of extreme points in linear programming. The concept of FDS was used in his seminal paper by Hakimi [13] and others thereafter in location problems. Yet, the term ‘finite dominating set’ is due to Hooker et al. [14]. In order to solve the TGP to optimality, an FDS must be identified, and then an exact algorithm (such as branch and bound) must be used.

In the next section, we present an example where an optimal solution is not necessarily a vertex of a triangle. In other words, we show that the set of vertices is not a finite dominating set for the 2.5D terrain guarding problem.

As discussed in Eliş et al. [6] and in more depth in ReVelle and Eiselt [16], in location problems, there are customers whose demand must be met by a number of facilities to be located on a surface. The goal is to minimize the number of facilities such that the demand of each customer is met. In this respect, TGP is also a location problem since guards, similar to facilities, are located on terrain to guard each point on the terrain. In a sense, each point on the terrain has a demand, which is being guarded, that needs to be met by the guards. 2.5D TGP is NP-Hard, as shown in Cole and Sharir [3].

When potential guard locations are identified, 2.5D TGP can be solved by Location Set Covering Problem (LSCP) formulation. LSCP is a set-covering problem within a location context. LSCP was introduced by Toregas et al. [17], and the problem formulation can be used for solving 2.5D TGP as follows,

$$\begin{aligned} {\text{Minimize}} & \quad \mathop \sum \limits_{j = 1}^{n} y_{j} \\ {\text{Subject to}} & \quad \mathop \sum \limits_{j = 1}^{n} a_{ij} y_{j} \ge 1,\quad \forall \,i = 1, \ldots,m. \\ & \quad y_{j} \in \{ 0,1\},\quad \forall j = 1, \ldots,n. \\ \end{aligned}$$

where yj is 1 if a guard is located at site j, and 0 otherwise. Each part of a terrain surface (part of a triangle) seen by each potential guard location is considered a demand element to be covered in the formulation. aij is 1 if the guard location j covers region i and 0 otherwise.

2.2 1.5D TGP

We note that 1.5D TGP can be solved to optimality by LSCP formulation as in 2.5D TGP once the set of guard locations is an FDS. Friedrichs et al. [11] presented the first FDS, and thus an optimal solution for 1.5D TGP. The FDS they have found has a size of O(n2). The regions covered by each potential guard location are taken to be a “witness set” such that guarding the elements of the witness set implies guarding of the terrain. The witness set in Friedrichs et al. [11] has a size O(n3). Ben-Moshe et al. [1] showed that there exists a witness set of size O(n2) before Friedrichs et al. [11]. Later, Eliş [7] showed a smaller finite dominating set and a smaller witness set, each of which has a size of O(n). Friedrichs et al. [11] posed the question of whether any optimal discretization exists, that is, whether an optimal FDS and an optimal witness set exist. A set is referred to as optimal if it has the minimum cardinality. In the next section, we show that the FDS found in Eliş [7] is optimal; that is, no other FDS for the problem has a smaller cardinality than O(n).

3 Analysis and Remarks

3.1 2.5D TGP

Consider the terrain shown in Fig. 8.3. The terrain is shaped like a football stadium such that the rectangle ABCD is at ground level, and the terrain rises from the edges of the rectangle. The horizontal lines passing through points 1–8 are the edges of tilted planar surfaces such that every cross-section of the terrain across the edges of AB and CD is like a staircase. Note that point P is inside a triangle and not a vertex. Consider, for example, the cross-section of the terrain along with the points 1-P-8 (Fig. 8.4). In each such cross-section, P (and possibly other nonvertex points) can guard the cross-section. Thus, P is an optimal solution (there may be alternative optimal points). We conclude that the set of vertices is not a finite dominating set and a finite dominating set needs to be identified in order to solve TGP to optimality by LSCP formulation.

Fig. 8.3
An illustration of a 2.5 dimensional terrain. A rectangular plot A B C D, has a triangle inside with a center point P. Following the point P, the rectangle is extended on either side with 4 points each, and the labels are, 1, 2, 3, 4, 5, 6, 7, 8 respectively.

A 2.5-dimensional terrain

Full size image
Fig. 8.4
An illustration of a cross section of the terrain. The center point P and points 1, 2, 3, 4 and 5, 6, 7, 8 on either sides. Points connected from 1 to P to 8 and 3 to P to 5 are indicated in dotted lines.

Cross-section of the terrain along with the points 1-P-8

Full size image

3.2 1.5D TGP

We use the same definitions and notations that are used in Eliş [7], which we give in the following. T denotes the terrain surface.

Convex region: Function h(x) may be convex in some intervals. The part of h(x) that is composed of maximally connected edges is referred to as a convex region. The set of convex regions is denoted by ‘CR’.

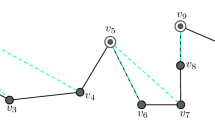
Convex point: A vertex where two convex regions intersect is referred to as a convex point. The two endpoints of T are included in the set of convex points, and the set of convex points is denoted by ‘C’, |C| = k. If k is the number of convex points, then the number of convex regions is k − 1 and vice versa. There are 11 vertices, 10 edges, 6 convex points, and 5 convex regions in Fig. 8.5. The part of T that is between convex points 5 and 6 is a convex region that has 4 edges.

Fig. 8.5
An illustration of a terrain with convex points and convex regions with labels 1, 2, 3, 4, 5, 6 on a surface 0 to L.

Convex points and convex regions on T

Full size image

Dip point: A point p on T “fully covers” N if N ⊆ VS(p). A point that is not a convex point and fully covers at least one convex region to its left and right, which are both different from the convex region it is in, is called a dip point. A dip point is illustrated in Fig. 8.6.

Fig. 8.6
An illustration of a cross section of a terrain with a dip point Q. Points connected from either side to Q is indicated with dashed and dotted lines.

Illustration of a dip point Q

Full size image

The set of dip points and convex points is referred to as critical points. Eliş [7] has shown that the set of critical points is an FDS and has a cardinality of O(n), and that the number of dip points is bounded by k − 1. Eliş [8] showed that there is even a smaller bound on the number of dip points, given by \(\frac{({\text{k}} - 2)}{2}\), and this bound is tight. In the following theorem, we show that the FDS of critical points is optimal in the sense that no other FDS for the problem can have a smaller cardinality.

Theorem

The FDS of critical points is optimal for 1.5D TGP in the sense that the number of points in any FDS is at least the number of critical points.

Proof

We note that an FDS is a set of points with predefined properties such that the points in FDS must be identifiable for all instances of TGP. Let X be an arbitrary FDS. Suppose, for example, that the points in X are defined such that the ith convex point is not in X. One can build an instance such that the ith convex point is the only optimal point. This can be done easily by constructing an example in which the height of the ith convex point is set at a value such that it is an optimal solution, i.e., the only point that can see both of its sides. Suppose, alternatively, that X does not contain a dip point. This implies that X, by construction, contains no nonconvex point that fully covers convex regions to its left and right, since if it contained, there would exist a dip point by definition. However, as shown in Fig. 8.6, there may exist an instance in which a dip point is the only optimal solution. Thus, X must contain convex points and dip points. Since X is arbitrary, together with the fact that the set of critical points is an FDS, it follows that the FDS of critical points is optimal.

We note that the points in an FDS correspond to the decision variables in the LSCP formulation. Thus, fewer points in the FDS imply that there will be fewer columns in matrix A(aij) of the formulation, which, in turn, implies that the solution time will be shorter. The following example compares the number of points in the FDS found in Friedrichs et al. [11] to that in Eliş [7], which is shown to be optimal by the above theorem. As illustrated by the terrain in Fig. 8.7, the number of points in the FDS of Friedrichs et al. [11] is more than three times the number of points in the FDS of Eliş [7].

Fig. 8.7
An illustration depicts a comparison of Friedrichs e t a l 2014 with 34 points to Elis 2017 hyphen 2 with 10 points. Dip point is indicated with an arrow.

A comparison of the FDS of Friedrichs et al. [11] to the optimal FDS of Eliş [7]

Full size image

4 Conclusions and Directions for Future Research

We have shown by a counter-example that the set of vertices is not a finite dominating set for 2.5D TGP. This implies that solving TGP to optimality is an open problem. Considering the important application areas of 2.5D TGP, future research may focus on finding an FDS for this problem. The type of points we have shown in the counter-example suggests that such points might belong to an FDS.

We have provided a partial answer to the research question posed in Friedrichs et al. [11] and shown that FDS of critical points found in Eliş [7] is optimal in the sense that no FDS exists with a cardinality smaller than O(n). Thus, future research efforts can be directed towards investigating an optimal witness set.