Parallel Fluid-Structure Interaction Simulation

Abstract

In this work we implement the parallelization of a method for solving fluid-structure interactions: one-field monolithic fictitious domain (MFD). In this algorithm the velocity field for solid domain is interpolated into fluid velocity field through an appropriate $L^2$ projection, then the resulting combined equations are solved simultaneously (rather than sequentially). We parallelize the finite element discretization of spatial variables for fluid governing equations and linear system solver to accelerate the computation. Our goal is to reduce the simulation time for high resolution fluid-structure interaction simulation, such as collision of multiple immersed solids in fluid.

1 Introduction

1.1 Fluid-Structure Interaction

Fluid-structure interaction (FSI) is a multiphysics problem that describes the interaction between a moving, sometimes deformable, structure and its surrounding incompressible fluid flow. In general, the solid materials deform largely and the deformations are strongly coupled to the flowing fluid. Numerical simulation of FSI is a computational challenge since the governing equations for solid and fluid regions are different and the algorithm needs to solve the locations of solid-fluid interfaces simultaneously with the dynamics in both regions where the kinematic (e.g., non-slipping) and dynamic (e.g., stress matched along the normal to solid-fluid interface) boundary conditions are imposed at the interface.

1.2 Numerical Scheme

In general, the numerical schemes for solving the FSI problems may be classified into two approaches: the monolithic/fully-coupled method [1,2,3] and the partitioned/segregated method [4, 5]. In addition, each method can be categorized further depends on the way to handle the mesh: fitted (conforming) mesh methods and unfitted (nonconforming) mesh methods.

Fitted mesh methods require solid and fluid meshes match each other at the interface, and both fluid and the solid regions share the nodes on the interface. In this way both a fluid velocity and a solid velocity (or displacement) are defined on each interface node. Clearly the fluid and solid velocities should agree on the interface nodes. Partitioned/segregated approach using fitted mesh to solve the governing equations. The solid and fluid equations are sequentially solved and then the steps are iterated until the velocities become consistent at the interface. This approach is easier to implement but not robust or fail to converge for problems where the fluid and solid appear to have significant energy exchange. On the other hand, monolithic/fully-coupled scheme solve the fluid and solid equations simultaneously on fitted mesh and often use a Lagrange Multiplier to weakly enforce the continuity of velocity on the interface. This method provides accurate and stable solutions but is computational challenging since one needs to solve the large size of nonlinear algebraic systems arising from the implicit discretization of the fully-coupled solid and fluid equations.

For unfitted mesh methods the solid and fluid regions are represented by two separate meshes and normally these do not agree to each other on the interface. Since there is no clear boundary for the solid problem, one of the approach to address the issue is to use Fictitious Domain method (FDM). In FDM the region representing solid is treated as (fictitious) fluid whose velocity/displacement is constrained to be the same as that of the solid. This constraint is enforced using a distributed Lagrange multiplier (DLM). There appear to be two situations for using unfitted meshes approach: either avoid solving the solid equations (such as Immersed Finite Element Method), or solve them with additional variables (two velocity fields and Lagrange multiplier) in the solid domain.

In this article, we parallelize one-field Fictitious Domain method can be categorized as a monolithic approach using an unfitted mesh. The main idea of the one-field FDM is as follows: (1) One-field formulation: re-write the governing equations for solid in the form of fluid equations. (2) $L^2$ projection (isoparametric interpolation): combining the fluid and solid equations and discretize them in an augmented domain. Then the problem is solved on a single field. The existing one-field FDM algorithm used in sequential simulation provide reasonable running time for 2D and 3D problems with low to moderate resolution, while its performance on highly resolved meshes ($256 \times 256 \times 256$ grid points and above) is not desired. Our goal is to accelerate the simulation algorithm using parallel computing and hope to extend its applications on FSI problems requiring high resolution, such as the 3D models describing the collision of multiple immersed solids in fluid.

2 Governing Equations and FEM Discretization

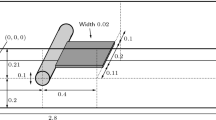
In this section we use a 2D FSI model (Fig. 1) to describe the governing partial differential equations (PDEs) for FSI. Denote the regions representing solid and fluid by $\varOmega _t^s \subset \mathbb {R}^d$ and $\varOmega _t^f \subset \mathbb {R}^d$, respectively. The subscript t reveals that both regions are time dependent. $\varOmega _t^s \cup \varOmega ^f_t$ is the fixed domain and the moving interface between solid and fluid is denoted by $\varGamma _t=\partial \varOmega _t^s \cap \varOmega _t^f$. Components of variables along spatial directions are indicated by subscripts i, j, k. In addition, the repeated indices are implicitly summed over. For instance, $u^s_j$ and $u^f_j$ represent the j-component (along the j direction) of the solid velocity and fluid velocity, respectively, $\sigma ^s_{ij}$ and $\sigma ^f_{ij}$ denote the ij-component for stress tensor of solid and fluid respectively, and $(u^s_i)^n$ is the i-component of solid velocity at time $t^n$. Quantities denoted by bold letters implies that variables are vectors or matrices.

Fig. 1.

2D FSI problem and the boundary conditions.

Let $\rho _s$ and $\rho _f$ be the density of solid and fluid respectively, $\tau _{ij}^s$ and $\tau _{ij}^f$ be the deviatoric stress of the solid and fluid respectively, $\mu ^f$ be the fluid viscosity, $p^f$ be the fluid pressure, and $g_i$ be the acceleration of gravity. Then the governing equations for incompressible fluid in $\varOmega _t^f$ as shown in Fig. 1 are

$$\begin{aligned} \dfrac{\partial u_{j}^f}{\partial x_j} = 0, \end{aligned}$$

(1)

$$\begin{aligned} \rho ^f \dfrac{D u^f_i}{D t} - \dfrac{\partial \sigma _{ij}^f}{\partial x_j} = \rho ^f g_i , \end{aligned}$$

(2)

$$\begin{aligned} \sigma _{ij}^f = \mu ^f \left( \dfrac{\partial u_i^f}{\partial x_j} + \dfrac{\partial u_j^f}{\partial x_i} \right) - p^f \delta _{ij} = \tau _{ij}^f - p^f\delta _{ij}, \end{aligned}$$

(3)

For the evolution of variables in solid domain $\varOmega _t^s$, we assume the solid is neo-Hookean incompressible solid and the governing equations are:

$$\begin{aligned} \dfrac{\partial u_{j}^s}{\partial x_j} = 0, \end{aligned}$$

(4)

$$\begin{aligned} \rho ^s \dfrac{D u^s_i}{D t} - \dfrac{\partial \sigma _{ij}^s}{\partial x_j} = \rho ^s g_i , \end{aligned}$$

(5)

$$\begin{aligned} \sigma _{ij}^s = \mu ^s \left( \dfrac{\partial x_i^s}{\partial X_k} \dfrac{\partial x_j^s}{\partial X_k} -\delta _{ij} \right) - p^s \delta _{ij} = \tau _{ij}^s-p^s\delta _{ij}. \end{aligned}$$

(6)

In the governing Eqs. (4)–(6), $\mu ^s$ and $p^s$ are the solid shear modulus and the pressure of the solid, respectively, $X_i$ represents the reference coordinates of the solid, and $x_i$ refer to the current coordinates of the solid or fluid. Therefore the deformation tensor of the solid is denoted by $\mathbf {F} =\left[ \partial x_i / \partial X_j \right]$. The incompressible neo-Hookean model described in Eqs. (4)–(6) can be used for predicting stress-strain behavior of materials undertaking large deformation [12]. Note that D/Dt in Eqs. (2) and (5) is the total time derivative and its form depends on what type of mesh (Eulerian or Lagrangian) used in the individual domain.

On the interface boundary $\varGamma _t$, the following conditions are imposed:

$$\begin{aligned} u^f_i = u^s_i, \end{aligned}$$

(7)

$$\begin{aligned} \sigma ^f_{ij} n_j^s = \sigma ^s_{ij} n_j^s , \end{aligned}$$

(8)

where $n_j^s$ is the component of unit normal to the interface pointing outward, see Fig. 1. Dirichlet and Neumann boundary conditions are imposed on the boundaries for the fluid accordingly:

$$\begin{aligned} u^f_i = u^s_i, \qquad \text{ on } \qquad \varGamma ^D \end{aligned}$$

(9)

$$\begin{aligned} \sigma ^f_{ij} n_j = \bar{h}_i \qquad \text{ on } \qquad \varGamma ^N. \end{aligned}$$

(10)

The initial conditions used in this work is:

$$\begin{aligned} u^f_i \mid _{t=0}= u^s_i \mid _{t=0} = 0 \end{aligned}$$

(11)

in which we assume the system starts from the rest.

The finite element discretization of the governing equations starts with weak formulation of Eqs. (1), (2), (4) and (5). Let $(u,w)_{\varOmega } = \displaystyle \int _{\varOmega } uv \text{ d }\varOmega$, and

$$ u_i=\left\{ \begin{array}{ll} u_i^f \quad \text{ in } \quad \varOmega ^f_t\\ u_i^s \quad \text{ in } \quad \varOmega ^s_t\\ \end{array} \right. $$

$$ p=\left\{ \begin{array}{ll} p^f \quad \text{ in } \quad \varOmega ^f_t\\ p^s \quad \text{ in } \quad \varOmega ^s_t\\ \end{array} \right. $$

Using constitution equations (3) and (6) with boundary condition in (10), integrating the stress terms by parts for the test functions $v_i \in H^1_0(\varOmega )$ and $q \in L^2(\varOmega )$, we get the weak formulation of the FSI system: finding $u_i \in H^1(\varOmega )$ and $p \in L^2_0(\varOmega )$ so that

$$\begin{aligned} \begin{array}{c} \rho ^f \left( \dfrac{D u_i}{D t}, v_i\right) _{\varOmega } +\left( \tau _{ij}^f, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega } - \left( p, \dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega } - \left( \dfrac{\partial u_i}{\partial x_j}, q \right) _{\varOmega } \\ + (\rho ^s-\rho ^f )\left( \dfrac{D u_i}{D t}, v_i\right) _{\varOmega ^s} + \left( \tau ^s_{ij}-\tau _{ij}^f, \dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega ^s} \\ = (\bar{h},v_i)_{\varGamma ^N} +\rho ^f(g_i,v_i)_{\varOmega } +(\rho ^s-\rho ^f)(g_i,v_i)_{\varOmega ^s}, \end{array} \end{aligned}$$

(12)

$\forall v_i \in H^1_0(\varOmega )$ and $\forall q \in H^1_0(\varOmega )$.

The integrals in Eq. (12) are calculated in all domains as illustrated in Fig. 1. Note that the fluid region is approximated by an Eulerian mesh and solid region is represented by an updated Lagrangian mesh in order to track the solid deformation/motion, therefore in these two different domains the total time derivatives are:

$$\begin{aligned} \dfrac{Du_i}{Dt} = \dfrac{\partial u_i}{\partial t}+u_j \dfrac{\partial u_i}{\partial x_j} \quad \text{ in } \quad \varOmega \end{aligned}$$

(13)

and

$$\begin{aligned} \dfrac{Du^s_i}{Dt} = \dfrac{\partial u^s_i}{\partial t} \quad \text{ in } \quad \varOmega ^s. \end{aligned}$$

(14)

Based on Eqs. (13) and (14), the time discretization of Eq. (12) becomes

$$\begin{aligned} \begin{array}{c} \rho ^f \left( \dfrac{u_i-u_i^n}{\varDelta t}+u_j \dfrac{\partial u_i}{\partial x_j}, v_i\right) _{\varOmega } +\left( \tau _{ij}^f, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega } - \left( p, \dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega } - \left( \dfrac{\partial u_j}{\partial x_j}, q \right) _{\varOmega } \\ + (\rho ^s-\rho ^f )\left( \dfrac{u_i-u_i^n}{\varDelta t}, v_i\right) _{\varOmega ^s_{n+1}} + \left( \tau ^s_{ij}, \dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega ^s_{n+1}} \\ = (\bar{h}_i,v_i)_{\varGamma ^N} +\rho ^f(g_i,v_i)_{\varOmega } +(\rho ^s-\rho ^f)(g_i,v_i)_{\varOmega ^s_{n+1}}, \end{array} \end{aligned}$$

(15)

where the superscript n of variable $u_i$ represents the velocity at the nth time step. Note that we have replaced $\varOmega ^s_{t^{n+1}}$, the solid mesh at the ($n+1$)th time step, by $\varOmega ^s_{n+1}$. By the spirit of splitting method introduced in [14], the above time evolution Eq. (15) can be viewed as the combination of two steps:

• 1. Convection step

  $$\begin{aligned} \rho ^f \left( \dfrac{u^{\star }_i-u_i^n}{\varDelta t}+u^{\star }_j \dfrac{\partial u^{\star }_i}{\partial x_j}, v_i\right) _{\varOmega } =0 \end{aligned}$$

  (16)

• 2. Diffusion step

  $$\begin{aligned} \begin{array}{c} \rho ^f \left( \dfrac{u_i-u_i^{\star }}{\varDelta t}, v_i\right) _{\varOmega } +\left( \tau _{ij}^f, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega } - \left( p, \dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega } - \left( \dfrac{\partial u_j}{\partial x_j}, q \right) _{\varOmega } \\ + (\rho ^s-\rho ^f )\left( \dfrac{u_i-u_i^n}{\varDelta t}, v_i\right) _{\varOmega ^s_{n+1}} + \left( \tau ^s_{ij}-\tau _{ij}^f, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega ^s_{n+1}} \\ = (\bar{h}_i,v_i)_{\varGamma ^N} +\rho ^f(g_i,v_i)_{\varOmega } +(\rho ^s-\rho ^f)(g_i,v_i)_{\varOmega ^s_{n+1}}, \end{array} \end{aligned}$$

  (17)

where the intermediate field $u^{\star }_i$ obtained from the convection step is used in the diffusion step to solve the “correct” field $u_i$. To obtain the system of linear algebraic equations, it is necessary to linearize Eqs. (16) and (17). The details of the linearization of both equations are described in [13] and we list the final linearized form as follows:

• 1. Linearized weak form convection step using Talyor-Galerkin method:

  $$\begin{aligned} (u^{\star }_i, v_i)_{\varOmega } = \left( u^n_i- \varDelta t u^n_j \dfrac{\partial u_i^n}{\partial x_j}, v_i\right) _{\varOmega } - \dfrac{\varDelta t^2}{2}\left( u^n_k\dfrac{\partial u_i^n}{\partial x_k} , u^n_j\dfrac{\partial v_i}{\partial x_j} \right) _{\varOmega } \end{aligned}$$

  (18)

• 2. Linearized weak form of diffusion step

  $$\begin{aligned}&\rho ^f \left( \dfrac{u_i-u_i^{\star }}{\varDelta t}, v_i\right) _{\varOmega } + (\rho ^s-\rho ^f ) \left( \dfrac{u^s_i-(u^s_i)^n}{\varDelta t}, v_i\right) _{\varOmega ^s_{n+1}} \nonumber \\+ & {} \mu ^f\left( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i}, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega } - \left( p,\dfrac{\partial v_j}{\partial x_j}\right) _{\varOmega } - \left( \dfrac{\partial u_j}{\partial x_j},q\right) _{\varOmega } \nonumber \\+ & {} \mu ^s\varDelta t \left( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i} + \varDelta t \dfrac{\partial u_i}{\partial x_k} \dfrac{\partial u^n_j}{\partial x_k} + \varDelta t \dfrac{\partial u^n_i}{\partial x_k} \dfrac{\partial u_j}{\partial x_k}, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega ^s_{n+1}}\nonumber \\+ & {} \varDelta t^2 \left( \dfrac{\partial u_i}{\partial x_k} (\tau _{kl}^s)^n\dfrac{\partial u^n_j}{\partial x_l} + \dfrac{\partial u^n_i}{\partial x_k} (\tau _{kl}^s)^n \dfrac{\partial u_j}{\partial x_l}, \dfrac{\partial v_i}{\partial x_j} \right) _{\varOmega ^s_{n+1}}\\+ & {} \varDelta t \left( \dfrac{\partial u_i}{\partial x_k} (\tau _{kj}^s)^n + (\tau _{il}^s)^n \dfrac{\partial u_j}{\partial x_l}, \dfrac{\partial v_i}{\partial x_j}\right) _{\varOmega ^s_{n+1}}\nonumber \\= & {} (\bar{h}_i,v_i)_{\varGamma ^N} +\rho ^f(g_i,v_i)_{\varOmega } +(\rho ^s-\rho ^f)(g_i,v_i)_{\varOmega ^s_{n+1}} \nonumber \\+ & {} \left( \mu ^s \varDelta t^2 \dfrac{\partial u^n_i}{\partial x_k} \dfrac{\partial u^n_j}{\partial x_k} + \varDelta t^2 \dfrac{\partial u^n_i}{\partial x_k} (\tau _{kl}^s)^n \dfrac{\partial u^n_j}{\partial x_l}- (\tau _{ij}^s)^n , \dfrac{\partial v_i}{\partial x_j} \right) _{\varOmega ^s_{n+1}} \nonumber \end{aligned}$$

  (19)

The spatial discretization in [13] uses a fixed Eulerian mesh for $\varOmega$ and an updated Lagrangian mesh for $\varOmega ^s_{n+1}$ to discretize Eq. (19). The discretization $\varOmega ^h$ (for $\varOmega$) uses $\mathbf {P}_2$ (for velocities $\mathbf {u}$) $\mathbf {P}_1$ (for pressure p) elements (the Taylor-Hood element) with the corresponding finite element spaces

$$\begin{aligned}&V^h(\varOmega ^h) = \text {span}\{ \psi _1, ... ,\psi _{N^u} \} \in H^1(\varOmega ) \\&L^h(\varOmega ^h) = \text {span}\{ \phi _1, ... ,\phi _{N^p} \} \in L^2(\varOmega ). \end{aligned}$$

The approximated solution $\mathbf {u}^h$ and $p^h$ can be expressed in terms of these basis functions as

$$\begin{aligned} \mathbf {u}^h( \mathbf {x}) = \displaystyle \sum ^{N^{ \mathbf {u}}}_{i=1} \mathbf {u}( \mathbf {x}_i) \psi _i( \mathbf {x}) \quad \mathrm {,}\quad p^h( \mathbf {x}) = \displaystyle \sum ^{N^{p}}_{i=1} p( \mathbf {x}_i) \phi _i( \mathbf {x}) \end{aligned}$$

(20)

The solid domain $\varOmega ^s_{n+1}$ at the $n+1$ time step is discretized as $\varOmega ^{sh}_{n+1}$ using linear triangular elements with the corresponding finite element spaces as:

$$\begin{aligned} V^{sh}(\varOmega ^{sh}_{n+1}) = \text {span}\{\psi ^s_1,...,\psi ^s_{N^s} \} \in H^1(\varOmega ^s_{n+1}), \end{aligned}$$

(21)

and approximate $\mathbf {u}^h( \mathbf {x}) \mid _{\mathbf {x} \in \varOmega ^{sh}_{n+1}}$ as:

$$\begin{aligned} \mathbf {u}^{sh}(\mathbf {x}) = \displaystyle \sum ^{N^s}_{i=1} \mathbf {u}^h( \mathbf {x}^s_i) \psi ^s_i(\mathbf {x})=\displaystyle \sum ^{N^s}_{i=1} \sum ^{N^u}_{j=1} \mathbf {u}( \mathbf {x}_j) \psi _j(\mathbf {x}_i^s) \psi ^s_i(\mathbf {x}) \end{aligned}$$

(22)

where $\mathbf {x}^s_i$ is the nodal coordinate of the solid mesh.

Substituting (20), (22) and similar expressions for the test functions $\mathbf {v}^h$, $q^h$ and $\mathbf {v}^{sh}$ into Eq. (18), we obtain the following matrix form:

$$\begin{aligned} \left[ {\begin{array}{cc} {\textbf {A}} &{} {\textbf {B}} \\ {\textbf {B}}^T &{} {\textbf {0}} \\ \end{array} } \right] \left[ {\begin{array}{c} {\textbf {u}} \\ {\textbf {p}} \\ \end{array} } \right] = \left[ {\begin{array}{c} {\textbf {b}} \\ {\textbf {0}} \\ \end{array} } \right] , \end{aligned}$$

(23)

where

$$\begin{aligned} \mathbf {A} = \mathbf {M} / \varDelta t + \mathbf {K} + \mathbf {D}^T( \mathbf {M}^s / \varDelta t + \mathbf {K}^s)\mathbf {D} \end{aligned}$$

(24)

and

$$\begin{aligned} \mathbf {b} = \mathbf {f}+\mathbf {D}^T\mathbf {f}^s + \mathbf {M}\mathbf {u}^{\star }/ \varDelta t + \mathbf {D}^T \mathbf {M}^s \mathbf {D} \mathbf {u}^n/ \varDelta t \end{aligned}$$

(25)

In Eqs. (24) and (25), matrix $\mathbf {D}$ is the isoparametric interpolation matrix derived from Eq. (22) which can be expressed as

$$\begin{aligned} \mathbf {D} = \left[ {\begin{array}{cc} {\textbf {P}}^T &{} {\textbf {0}} \\ {\textbf {0}} &{} {\textbf {P}}^T \\ \end{array} } \right] \quad \mathrm {,}\quad \mathbf {P}_{ij} = \psi _i(\mathbf {x}^s_j). \end{aligned}$$

(26)

For the other matrices in (24) and (25), ${\textbf {M}}$ and ${\textbf {K}}$ are global mass matrix, global stiffness matrix from discretization of integrals in $\varOmega ^{h}$. Similarly, ${\textbf {M}}^s$ and ${\textbf {K}}^s$ are mass matrix and stiffness matrix from discretization of integrals in $\varOmega ^{sh}$. ${\textbf {u}}$, ${\textbf {p}}$, ${\textbf {f}}$ are velocity, pressure and right hand side vectors, respectively. ${\textbf {B}}$ and its transpose ${\textbf {B}}^T$ represent the connections between pressure and velocities, which arise from the weak formulation in (19).

3 Parallelization of One-Field FDM Algorithm

3.1 Parallelism and Related Issues

The algorithm described in the previous section consists three parts: finite element discretization of the PDEs (calculation of element matrices, assembly of the global matrix), projecting matrix arising from solid equations into matrix arising from fluid equations ($L^2$ isoparametric projection) and solving the resulting system of linear algebraic equations. The computations of the first two parts are nearly embarrassingly parallel and require little or no communication, while the linear system solving using iterative scheme needs global communications (inner product) and communications from neighboring processes (matrix vector multiplications) for updating the residual and solution vectors.

3.2 Datatype and Computation Setup

The code implementation for solving the model described in the previous section is carried out in Campfire, where the structure grid generation is provided by PARAMESH. PARAMESH generates meshes as the union of blocks (arrays) of cells. Each block consists of internal cells and certain layer of guardcells (Fig. 2). In finite element implementation each cell is treated as an (quadrilateral) element. For the 2D FSI simulation there are three variables to be solved: u (x-velocity), v (y-velocity) and p (pressure). For spatial variables we discretize the velocity field by quadratic quadrilateral (P2) elements and the pressure by linear quadrilateral (P1) elements. To accomplish storing the variable values in a 2D model, we employ four arrays from PARAMESH.

Fig. 2.

A $2\times 2$ block with one layer of guardcells

3.3 Linear System Solver

As known, the solution of a linear system of equations constitutes an important part of the algorithm for solving PDEs numerically. Thus the properties of the linear system solver is crucial to the performance of PDE simulations. Generally, iterative methods consist of three core computational steps, which are vector update, matrix-vector multiplications and inner product computation. Vector updates is inherently parallel and there is no communication required. Parallel algorithm for matrix-vector multiplication relies on the data structure of matrix (sparsity, organization etc.) and typically local data communications between neighboring processes are sufficient for correct computation. Inner product calculation requires global data communications but the complexity could be moderate ($O(\log _2 P)$, where P is the number of processes). The parallel implementation of these three computation kernels will provide significant performance enhancement on iterative methods. To accelerate the MINRES iteration we use incomplete LU as the preconditioner. The computations for applying preconditioners involve backward/forward substitutions, which is inherently sequential. In the parallel implementation the preconditioner becomes block Jacobi type and the matrix entries connecting the neighboring processes are ignored. This causes the convergence properties of parallel preconditioning deteriorate significantly from sequential preconditioning.

4 Numerical Experiments

In this work, we exam our parallel code on two 2D problems and compare the performance of parallel computation with the serial version in each case to access the parallel efficiencies. MINRES iterations stop when the 2-norm of the relative residual is less than $10^{-8}$ or the maximum number of iterations is reached (7500). For parallel simulations we use various number of processes up to 256 cores. All simulations were carried out on Taiwania, a supercomputer having a memory of 3.4 petabytes and delivering over 1.33 quadrillion flop/s of theoretical peak performance. The system has 630 compute nodes based on 40 core Intel Xeon Gold 6148 processors running at 2.4 GHz. Overall the system has a total of 25200 processor cores and 157 TB of aggregate memory. All the timing results are the average values from the running time of multiple simulations.

Fig. 3.

A disc in lid-driven cavity flow with the boundary conditions.

Table 1. Parameters for 2D solid (disc) in a lid-driven cavity flow

4.1 The Motion of a Disc in 2D Lid-Driven Cavity Flow

In the first case we consider the motion of a deformable disc in a lid-driven cavity flow in 2D domain. Zhao et al. [15] studied the simulation for validating their methods. The experiment parameters are shown in Table 1 and Fig. 3 is the graphic demonstration of the problem setup. Initially, a round stress-free disc of radius 0.2 is centered at (0.6, 0.5), then at $t=0$ the top cavity wall starts moving horizontally at $u=1$. For the material parameters, the density of the disc ($\rho _s$) and fluid ($\rho _f$) are both set to be 1. The elastic constant ($\mu _s$) of the disc is 0.1 and the viscosity of the fluid ($\mu _f$) is 0.01.

The fluid mesh resolution of the numerical simulation is $128 \times 128$, solid mesh contains 31163 elements and 15794 nodes. $\varDelta t=0.01$, 800 time steps. The running time for the last 100 time steps and speedup are shown in Table 1. As seen from the table, our method gains a roughly 47 speedup for 256 cores parallel simulations. Comparing with serial simulation, we reduce the overall running time (need 800 time steps) from roughly 65 h to 1.5 h. In the table we also list the average number of preconditioned MINRES iterations for the first 100 time steps in each simulation to show the impact of the parallelized preconditioning on the convergence of MINRES iterations. Notice that the number of MINRES iterations reach the maximum threshold (10000) after $t = 0.3$, corresponding to the scenario when the disc is near the wall.

Table 2. Parallel simulation results

Fig. 4.

The simulation results for a deformable solid motion in a lid-driven cavity flow.

The solid deformation are visualized in Fig. 4. The motion and the deformation of the solid are nearly identical to the result from [13] and [15]. We see that the disc deformation is asymmetric about the disc’s vertical center line, and lubrication forces prevent the disk from touching the lid. The solid body ends up in a fixed position near the center of the cavity, and the velocity field becomes steady.

For the parallel simulation we gained speed up factor of 44 for 256 processes, corresponding to parallel efficiency of $17\%$. The increased number of MINRES iteration explains the reduction of the parallel efficiency from $82\%$ (4 processes) to $17\%$ (256 processes) (Table 2).

4.2 Oscillation of a Flexible Leaflet Oriented Across the Flow Direction

The second example comes from [10,11,12], in which the problem was used for validation their methods. In this work we parallelize the one field monolithic FSI algorithm of this benchmark problem in [13]. The problem setup is described as follows. A leaflet is located at the center of the bottom horizontal side of a rectangular computational domain. The horizontal length and vertical length are 4 m and 1 m, respectively. The inflow velocity is in the x-direction and governed by $u_x=15.0 y (2-y) \sin (2\pi t)$. The computational domain and boundary conditions are illustrated in Fig. 5.

Fig. 5.

Source: [13]

Oscillation of a flexible leaflet across the flow direction.

The material parameters for the solid and fluid are listed in Table 3. The leaflet (solid region) is represented with 154 linear triangular elements with 116 nodes, and the corresponding fluid mesh is consist of $320 \times 80$ rectangular cells. The time step size for the evolution is $\varDelta t = 5 \times 10^{-5}$ s. All leaflet simulations run from $t=0$ to $t=0.8$, which is 16000 time steps. Similar to the above example, we record simulation time for the middle 2000 time steps and the speedups of the parallel run are listed in Table 4. In this case the ratio of the number of solid mesh nodes to the number of fluid mesh nodes is much smaller than the example 1. For 256 processes simulation we gained a speed up factor of 28 corresponding to $11\%$ parallel efficiency. Obviously the convergence of the preconditioned MINRES in this case is much worse than that in the example 1. This may attribute to the high elastic modulus ($10^{7}$ vs. 1) of the solid and the convergence of MINRES is more difficult (Fig. 6).

Table 3. Material parameters for oscillation of a flexible leaflet oriented across the flow direction.

Table 4. Parallel simulation results: leaflet in 2D channel flow

Fig. 6.

The simulation results for oscillation of a flexible leaflet oriented across the flow direction.

5 Conclusion

In this research we have implemented the parallel computation on FSI 2D problem simulations. The convergence of preconditioned MINRES iteration is crucial to the parallel efficiency of the algorithm. For the first benchmark problem (2D disc in cavity-driven flow) the parallel simulation gain significant speed up although the parallel efficiency is not impressive. However, high elastic modulus of solid appeared in the second example (oscillating leaflet in channel flow) reduces the convergence performance of MINRES and hence the computation performance and parallel efficiency. One of the most important future work is to find preconditioners whose properties are minimally impacted by parallelization. With the modified preconditioner and algorithm we wish to extend our experiment to 3D FSI benchmark problems to verify our method.